Abstract
Many existing approaches for asymmetric damped system are based on the assumption that the eigenvalues are simple or semisimple with separated derivatives. This paper presents a new algorithm for computing the derivatives of the semisimple eigenvalues and corresponding eigenvectors of asymmetric damped system. Compared with the existing methods, the algorithm can be applicable to problems whether the repeated eigenvalues have well separated derivatives. In the proposed method, the derivatives of eigenvectors are divided into a particular solution and a homogeneous solution, where the particular solution is constructed by using generalized inverse matrix. The effectiveness of the proposed algorithm is illustrated by one numerical example.
1. Introduction
In the past decades, damped system has become a topic of great interest to researchers because it arises frequently in many areas such as applied mechanics, electrical oscillation, vibro-acoustics, fluid dynamics, signal processing and so on. In this paper, we consider the equation of damped system with the following form [1]:
where the matrices , and are asymmetric and damping is non-proportional.
Studies on the sensitivity analysis of damped system have widely used in damage detection [2], system identification [3], carbon nanotube vibration [4], model updating [5, 6] and many other disciplines. The fundamental objective of sensitivity analysis is to compute the derivatives of eigenvalues and eigenvectors. Research on this topic has received much attention and many different algorithms [7-18] have been developed in a recent treatise. Most of the existing algorithms can be divided into two categories. The first category is to convert the damp system to undamped system by using linearization [7-9]. The second category is to differentiate Eq. (1) and compute the derivatives of eigenvectors directly [10-18]. Although there are various algorithms for damped system, most of existing approaches are based on the assumption that the eigenvalues are simple or semisimple with separated derivatives. In order to fill this gap, Qian et al. [19] relaxed the restriction that the repeated eigenvalues must have well separated derivatives and presented a new algorithm for computing eigensensitivity of damped system by utilizing the method of [20]. By using generalized inverses, Wang and Dai [21] introduced a method for computing the first-order derivatives of eigenvalues and eigenvectors for symmetric damped system.
Different from symmetric damped system, eigenvalues of an asymmetric damped system have different right and left eigenvectors. Therefore, the eigenvectors may be not unique by one normalization. By adopting an additional normalization to guarantee the uniqueness of the eigenvectors, we extend the method of [21] to asymmetric damped system in this paper. we derive the first-order derivatives of right and left eigenvectors regardless of whether the eigenvalues have multiple derivatives.
The structure of this paper is divided into five parts. We begin in Section 2 with a brief description of algorithm for eigenvalue derivatives, and Section 3 gives a comprehensive discussion on the derivations of the eigenvector in two cases according to whether the derivatives of the eigenvalue have multiple roots. A numerical example is presented to illustrate effectiveness of the proposed algorithm in Section 4. Section 5 concludes the paper with some final remarks.
2. Calculation of eigenvalues derivatives
We consider the damped system with parameters . Suppose that is the eigenvalue and , are the corresponding right and left eigenvectors respectively, i.e.:
where , and are asymmetric analytic matrices and is nonsingular in this paper.
We consider the algorithm for eigenpair derivatives of Eq. (2) with multiple eigenvalue. For this reason, we suppose that is the semisimple eigenvalue with multiplicity at and the column vectors of , are the right and left eigenvectors respectively. From lemma 3 in Ref. [22], is non-singular. Without loss of generality, let , satisfy:
Suppose and the eigenvector subsets:
are the eigenvalues functions and corresponding eigenvectors functions when varies at the neighborhood of . Then:
where , satisfy:
It is well known that the eigenvectors given by Eqs. (4), (5) and (6) are nonunique to the extent of a non-zero constant, and another normalized condition should imposed to result in unique eigenvectors and thereafter, for one to solve the corresponding eigenvectors derivatives. Because the mass matrix is not positive definite, the conventional mass normalization is not used. In this paper, the normalizing condition in Ref. [15] is adopted. Suppose:
The normalizing condition of is:
Because the linear combinations of eigenvectors corresponding to eigenvalues are also eigenvectors of , we can express , by the differentiable eigenvector subset , in the following manner:
For the sake of simplify notation, is omitted for variables evaluated at . Using Eq. (6) at , we have:
Then:
i.e., is the inverse of .
In order to compute and , let , , where denotes the derivative of . Differentiating both sides of Eqs. (2) and (3) with respect to and letting , one has:
where Premultiplying each side of Eq. (11) by one obtains:
Substituting Eq. (9) into Eq. (13), we have:
where Eq. (14) shows that diagonal elements of matrix are eigenvalues of and matrix are corresponding right eigenvectors matrix. Hence, solving eigenproblem yields eigenvalues derivative and matrix .
3. Calculation of eigenvectors derivatives
In this section, we will present a comprehensive discussion on the derivations of the eigenvectors according to whether the derivatives of the eigenvalues have multiple roots.
Case 1. The eigenvalues of Eq. (14) are distinct . In this case, by solving Eq. (14) one can obtain the eigenvalue derivative and the corresponding eigenvector matrix uniquely up to scalar multipliers, and then are determined by the relation and normalizing condition Eq. (7). In order to obtain we introduce the generalized inverse matrix of matrix , i.e. satisfies . Then will be a particular solution of Eq. (11) and the general solution of Eq. (11) can be expressed as:
where is a constant matrix. Let , , we will get another particular solution of Eq. (11) by taking in Eq. (15):
where . Because:
where , then:
where is a restricted generalized inverse of [10], and satisfies:
Therefore, the solution of Eq. (11) can be written as:
The computation of matrix need employ the second-order differential information of Eq. (2):
where:
Premultiplying each side of Eq. (20) by , yields:
where , then:
Using the similar discussion about Eq. (11), one can express the general solution of Eq. (20) as:
where . By the relation , one has:
Then:
where . Substituting Eq. (24) into Eq. (21), rearranging the equation yields:
Then we can get the off-diagonal elements of matrix :
The diagonal elements of can be determined from Eq. (7). Let , by Eq. (7) and Eq. (19) one has:
Then:
So:
Repeat the above process with Eq. (12), we have the derivatives of left eigenvectors:
where and the off-diagonal elements of can be determined by:
where:
Differentiating both sides of Eq. (6) and letting , we get:
Then, we complete the process for computing derivatives of eigenvectors when the eigenvalues of Eq. (14) are distinct.
Case 2. Eq. (14) has repeated eigenvalues. Suppose that the eigenvalues of Eq. (14) are with multiplicity is , , then . The right and left eigenvectors is defined:
Because the eigenvectors are not uniquely determined when eigenvalues have repeated roots, and , and then and , are not uniquely defined. Let:
where and are coefficient matrices. Dividing Eq. (26) into block forms and substituting Eqs. (34) and (35) into it, one obtains:
where:
Premulitiplying each side of Eq. (37) by with , yields a standard eigenvalue problem:
Suppose the eigenvalues of Eq. (40) are distinct, and are uniquely determined to the extent of an non-zero constant multiplier by Eq. (40), then , are uniquely determined by the normalized condition Eq. (7). By the relation , are also determined, and then , are also uniquely identified by Eqs. (36) and (17). So, the result of also becomes determination of the off-diagonal elements of because the relation Eq. (30) is also right. On both sides of Eq. (37), we take :
To extra the off-diagonal elements of and use the third derivative of Eq. (2), we obtain following relation by Eqs. (17), (26), (31):
where:
Taking out the diagonal block equation, one has:
Then:
where is the th diagonal element of . From Eq. (44), one has:
The derivatives of left eigenvectors can be computed by similar method. Then, we complete the process of computing the derivatives of eigenvectors in two cases. Formally, an algorithm based on the above procedure can be designed as following.
Algorithm procedure for computing the eigenpair derivatives:
Step 1. Input: Matrices , , and the first to third order derivatives of , , , the repeated eigenvalue and corresponding right and left normalized eigenvectors matrices , .
Step 2. Compute:
The generalized inverse of and .
Step 3. Obtain the eigenvalue derivatives by computing the eigenproblem
Step 4. When the eigenvalue derivatives are distinct, then obtain , and by Eqs. (8) and (17), then get , by Eqs. (29) and (32).
Step 5. If the eigenvalues of have repeated roots, calculate:
Solve the eigenproblem , compute , and by Eqs. (35) and (17) and , by Eqs. (41) and (45), (30).
Step 6. Calculate
Step 7. Output: , .
The computational cost of the Algorithm is , where the generalized inverse of matrix is calculated by the singular value decomposition of .
4. Numerical illustration
To illustrate the effectiveness of the proposed algorithm, we carried out one numerical example shown in Fig. 1. All the following calculations used MATLAB2015b.
In Fig. 1, there are five springs, four damping and three disks. In order to obtain asymmetric damped system, we suppose that the system is rotated with high speed in a container. From Fig. 1, we can get the mass, stiffness and damping matrices of the system:
We assume that the system has the following gyroscopic matrix:
Fig. 1An asymmetric damped system
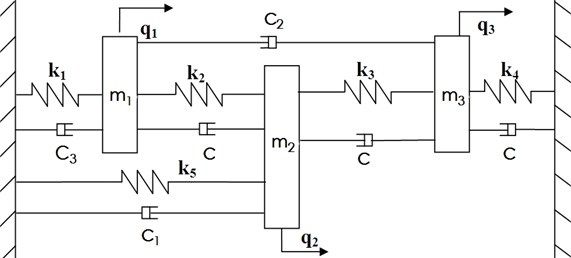
Then, we can get the damped matrix of the asymmetric system by the relation:
Setting 1 kg, 1000 N/m, 0 N/m, 10 N s/m. We select as the design parameter and consider 0. Then:
The eigenvalues of the damped system are at 0 and the corresponding eigenvectors are:
By Eq. (12) we have:
This means the derivatives of eigenvalues are equal. Using Eq. (40), we get:
Then we derive the adjacent right and eigenvectors , and the right eigenvectors derivatives as following:
To examine the correctness of the above results, we give the parameter a small perturbation 0.1. We compute the eigenpair of perturbed system at and compare the result with the linear approximation of perturbed system by Taylor series. Table 1 and Table 2 show the comparisons of the eigenvalues and eigenvectors.
Table 1Comparison of eigenvalues
Original eigenvalue | Approximated eigenvalues | Perturbed eigenvalues | Errors |
–5–31.225 | –5.1–31.2088 | –5.1–31.2088 | 8.5e-8 |
–5.1015–31.2086 | –5.1015–31.2086 | 1.5e-5 |
Table 2Comparison of right eigenvectors
Original eigenvectors | Approximated eigenvectors | Perturbed eigenvectors | Errors |
1.0000 | 1.0000 | 1.0000 | 0 |
–0.3333 | –0.3333 | –0.3333 | 8e-14 |
5000 | 0.5000 | 0.5000 | 0 |
0 | 0.0300 | 0.0303 | 3e-4 |
1.0000 | 1.0000 | 1.0000 | 0 |
0 | 0 | 0 | 3e-11 |
5. Conclusions
Derivatives of eigenvalues and eigenvectors of parameter-dependent matrix eigenproblems play a key role in the optimum design of structures in engineering. In this paper, we extend the method of [21] to asymmetric damped system and develop a numerical algorithm for computing the eigenpair derivatives by adopting a new normalization to guarantee the uniqueness of the eigenvectors. The proposed algorithm divides the eigenvectors derivatives into a particular solution and a homogeneous solution, where the particular solution to the governing equations is constructed by using the generalized inverse matrix. The present study is the first step for the research of eigensensitivity of damped systems. The higher order derivatives of eigenvalues and eigenvectors will be challenges for further research.
References
-
Wang P. X., Dai H. Calculation of eigenpair derivatives for asymmetric damped systems with distinct and repeated eigenvalues. International Journal for Numerical Methods in Engineering, Vol. 103, 2015, p. 501-515.
-
Messina A., Williams E. J., Contursi T. Structural damage detection by a sensitivity and statistical-based method. Journal of Sound and Vibration, Vol. 216, 1998, p. 791-808.
-
Adhikari S. Structural Dynamics with Generalized Damping Models: Identification. Wiley-ISTE, 2013.
-
Yayli M. O. A compact analytical method for vibration analysis of single-walled carbon nanotubes with restrained boundary conditions. Journal of Vibration and Control, Vol. 22, 2016, p. 2542-2555.
-
Yuan Y. X., Liu H. An iterative method for solving finite element model updating problems. Applied Mathematical Modelling, Vol. 35, 2011, p. 848-858.
-
Friswell M. I., Mottershead J. E. Finite Element Model Updating in Structural Dynamics. Kluwer Academic, Norwell, 1995.
-
Brandon J. A. Second-order design sensitivities to assess the applicability of sensitivity analysis. AIAA Journal, Vol. 29, 1991, p. 135-139.
-
Zeng Q. H. Highly accurate modal method for calculating eigenvector derivative in viscous damping systems. AIAA Journal, Vol. 32, 1994, p. 746-751.
-
Liu X. B. A new method for calculating derivatives of eigenvalues and eigenvectors for discrete structural systems. Journal of Sound and Vibration, Vol. 332, 2013, p. 1859-1867.
-
Tang J., Ni W. M., Wang W. L. Eigensolutions sensitivity for quadratic eigenproblems. Journal of Sound and Vibration, Vol. 196, 1996, p. 179-188.
-
Adhikari S. Rates of change of eigenvalues and eigenvectors in damped dynamic systems. AIAA Journal, Vol. 37, 1999, p. 1452-1458.
-
Adhikari S., Friswell M. I. Eigenderivative analysis of asymmetric non-conservative systems. International Journal for Numerical Methods in Engineering, Vol. 51, 2001, p. 709-733.
-
Choi K. M., Jo H. K., Kim W. H., Lee I. W. Sensitivity analysis of non-conservative eigensystems. Journal of Sound and Vibration, Vol. 274, 2004, p. 997-1011.
-
Guedria N., Smaoui H., Chouchane M. A direct algebraic method for eigensolution sensitivity computation of damped asymmetric systems. International Journal for Numerical Methods in Engineering, Vol. 68, 2006, p. 674-689.
-
Xie H. Q., Dai H. Derivatives of repeated eigenvalues and corresponding eigenvectors of damped systems. Applied Mathematics and Mechanics (English Edition), Vol. 28, 2007, p. 837-845.
-
Xie H. Q., Dai H. Calculation of derivatives of multiple eigenpairs of unsymmetrical quadratic eigenvalue problems. International Journal of Computer Mathematics, Vol. 85, 2008, p. 1815-1831.
-
Wang P. X., Dai H. Eigensensitivity analysis for symmetric nonviscously damped systems with repeated eigenvalues. Journal of Vibroengineering, Vol. 16, 2014, p. 4065-4076.
-
Wang P. X., Dai H. Calculation of eigenpair derivatives for symmetric quadratic eigenvalue problem with repeated eigenvalues. Computational and Applied Mathematics, Vol. 35, 2016, p. 17-28.
-
Qian J., Andrew A. L., Chu D., Tan R. C. E. Computing derivatives of repeated eigenvalues and corresponding eigenvectors of quadratic eigenvalue problems. SIAM Journal on Matrix Analysis and Applications, Vol. 34, 2013, p. 1089-1111.
-
Andrew A. L., Tan R. C. E. Computation of derivatives of repeated eigenvalues and the corresponding eigenvectors of symmetric matrix pencils. SIAM Journal on Matrix Analysis and Applications, Vol. 20, 1989, p. 78-100.
-
Wang P. X., Dai H. Eigensensitivity of symmetric damped systems with repeated eigenvalues by generalized inverse. Journal of Engineering Mathematics, Vol. 96, 2015, p. 201-210.
-
Andrew A. L., Chu K. W. E., Lancaster P. Derivatives of eigenvalues and eigenvectors of matrix functions. SIAM Journal on Matrix Analysis and Applications, Vol. 14, 1993, p. 903-926.
About this article
This work was supported by National Natural Science Foundation of China (Nos. 61503160, 11571171 and 61572242) and Natural Science Foundation of the Jiangsu Higher Education Institutions of China (No. 15KJB110004).
