Abstract
To accurately detect an early transverse crack in the rotating machinery caused by fatigue or creep, various kinds of diagnosis systems utilizing the steady-state responses of a cracked rotor were developed. The paper focuses on the non-stationary response of a rotor system such as the startup, the shutdown or the variable running speeds of a rotating machinery to detect a transverse crack and to overcome the defects of the diagnosis system utilizing steady-state responses. Non-stationary characteristics during passages through the major resonance and various kinds of resonances are studied numerically and experimentally. The results demonstrate that the changes of vibration characteristics in a non-stationary response can detect a crack in a wide rational speed range and also prevent the dangerous operation for detecting a crack.
1. Introduction
A transverse crack easily occurs in the rotating machinery during the operation due to fatigue, creep or above both them. To prevent a serious accident caused by a crack, it is very important to discover the crack at the early stage of the crack propagation. Various kinds of diagnosis system have been developed to diagnose a crack in the rotating machinery [1-8]. The crack’s diagnostic methods are classified into two conditions. The static examination is that a rotating machinery is dissolved and the parts are examined independently. The dynamic examination is that the changes of the vibration characteristics are analyzed during the operation.
To detect a crack in the rotor system, scholars have mostly concentrated on the changes of vibration characteristics in the steady-state responses of a cracked rotor. Li et al. proposed a novel method based on the symbolic dynamic filtering (SDF) for early fault detection and intrinsic characteristic-scale decomposition (ICD) for fault type recognition [9]. Li et al. put forward a new bearing vibration feature extraction method based on the multiscale permutation entropy (MPE) and improved support vector machine based binary tree (ISVM-BT) to accomplish the fault identification automatically [10]. Ebrahimi et al. developed a novel continuous model for flexural vibration of rotors with an open edge crack [11]. Castejon et al. applied the discrete wavelet transform theory and multiresolution analysis (MRA) to vibration signals to find characteristic patterns of shafts with a transversal crack. In addition, the feature vectors are used as input to an intelligent classification system based on artificial neural networks (ANNs) [12]. Ishida observed a sub-harmonic oscillation of order 1/2, a super sub-harmonic oscillation of order 3/2 and a summing-and-differential harmonic oscillation owning to a crack in experimental setup [13, 14]. Al-shudeifat and Butcher proposed two new breathing functions to represent the actual breathing effect on the cracked element stiffness matrix [15]. Ishida investigated non-stationary responses at the 1/2 order sub-harmonic Oscillation [16]. Li and Zhang used the Hilbert-Huang Transform (HHT) to identify a crack in a rotor-bearing system under non-stationary oscillations [17, 18]. However, Wang et al. proposed the application of order tracking to investigate a crack when the rotor system has a varying speed [19]. Therefore, there is a possibility that those oscillations also occur in practical machines under stationary responses or non-stationary responses.
Most of the dynamic monitoring systems focus on the changes of vibration characteristics in the steady-state oscillation. They have the following defects. First, many characteristics owing to a crack do not occur in the rotational speed range. Therefore, it is impossible to detect them during the normal operation. In addition, when some changes occur due to a crack, it is dangerous to investigate the characteristics of the resonance range because there is a possibility that the crack develops rapidly during the investigation.
This study focuses on a practical detection method using non-stationary vibrations to overcome above those defects. When a rotating machine starts up or shuts down, the rotor system sweeps all over the rotational speed range below rated speed. If these non-stationary resonances are used to detect a crack, the above defects of diagnosis system with the steady-state resonance could be avoided.
In the paper, a typical open-close model is used to investigate the characteristics of non-stationary oscillations of a cracked rotor during the passages through the major critical speed and various kinds of subcritical speeds. Particularly, the study focused on the influences of an angular acceleration and the magnitude and phase of an unbalance for the maximum amplitude. The effectiveness of the method is verified systematically through numerical simulations and many experiments.
To illustrate the method to detect a crack, the next section proposes the theoretical modeling and the motion equations. Using the change of the characteristics of non-stationary oscillations passing through the harmonic resonance are explained in Sections 3. Non-stationary oscillation during passages through a forward super-harmonic and a forward sub-harmonic resonance are interpreted and summarized in Section 4. The experimental setup and results are presented in Section 5. Finally, the concluding discussion is given in Section 6.
2. Theoretical modeling and motion equations
2.1. Theoretical Modeling
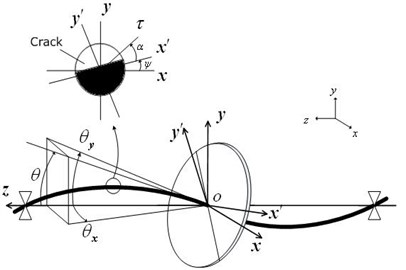
The theoretical model and the coordinate systems are shown in Fig. 1. When the disk is not located at the shaft center, the rotor system where the deflection and the inclination couple each other is a four-degree-of-freedom (4DOF). On the contrary, if the rotor is located at the shaft center, it can be divided into two separate 2DOF systems, that is, a deflection model (the Jeffcott rotor) and an inclination model. In the latter system, the natural frequencies change due to the gyroscopic moment similar to the 4DOF model [20]. Therefore, the inclination model in the theoretical analysis is used in the study. The origin of the Cartesian coordinate system - is at the midpoint of the bearing centerline. The -axis coincides with the breath ring centerline. The inclination angle of the elastic shaft at the disk mounting position can be expressed by and its projection angles of to the and – planes can be expressed by and shown in Fig. 1, respectively. It is supposed that a crack appeared in the half of the shaft. The rotating coordinate system - is also considered where the -axis coincides with the crack boundary. The projection angles of to - and -planes can be represented by and , respectively. When the crack is opened and , the stiffness of the shaft becomes small. When the crack is closed and , the shaft stiffness returns to the same value as the shaft with no crack. Therefore, the restoring moment has the spring characteristics with a piecewise linearity and its components and in the and – planes, respectively, are represented as follows:
where, and are the spring constants and is the directional difference.
Fig. 1Model of a cracked rotor and coordinate systems
2.2. Motion Equations
The ratio of the polar inertia moment to the diametric inertia moment can be represented by , the rotational speed and the damping coefficient can be represented by and , respectively. The dynamic unbalance’s magnitude and its phase angle can be expressed by and , respectively. The rotational angle of -axis is represented by . Corresponding to the gravitational force, the constant moment which works in the -direction is considered. The motion equations governing non-stationary oscillations in a symmetrical 2DOF inclination model with no crack is given by Ishida and Yamamoto [20]. First, the Eq. (1) is transferred into the expression of the stationary coordinate system. By replacing the part representing the restoring force in symmetrical system by this expression, the motion equations for a cracked rotor can be obtained as follows:
where , , . As for the symbol “” in the motion equations, all upper signs are showed for and all lower signs are also showed for .
The above motion equations have the dynamical characteristics as follows: (1) time-varying coefficients similar to the asymmetrical rotor, (2) rotating piecewise nonlinearity and (3) unbalance excitation.
3. Non-stationary oscillations
3.1. Condition of a vertical rotor
This section explains non-stationary characteristics of a cracked rotor. The governing motion equations of are given by putting in Eq. (2). The acceleration of a rotor is a constant , no matter what acceleration or deceleration. The angular position of the -axis can be gotten by:
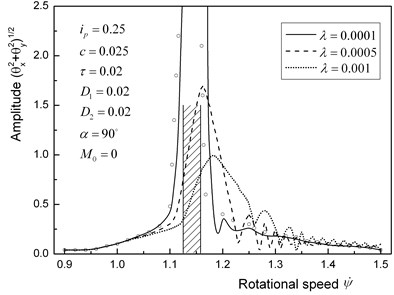
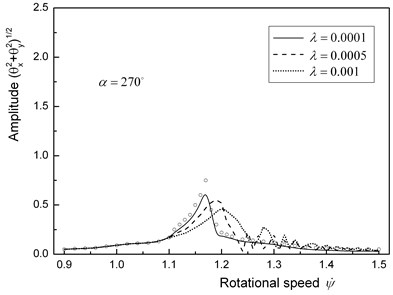
The response curves are shown by full lines in Fig. 2, and the curves are obtained numerically by the Adams method. The results for three kinds of angular acceleration are shown. For comparison, the amplitudes of steady-state oscillations () are also shown by the symbol ∘. is an initial angular velocity.
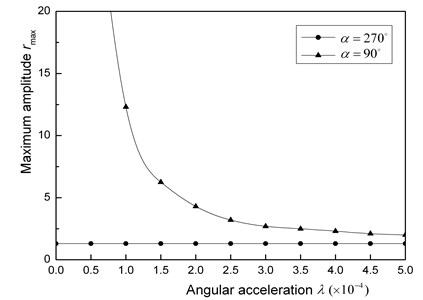
When the unbalance and the crack are on the same side, a result is shown as Fig. 2(a). In this case, an unstable range exists. If the rotational speed of a rotor sweeps this unstable range, the large amplitude appears for the small angular acceleration . If they are on the opposite side, another result is shown as Fig. 2(b). Since there no exists an unstable range, the amplitude is comparatively small, no matter what any value of . Fig. 3 shows that the maximum amplitude changes with . If the unbalance and the crack are on the same side, the cracked rotor cannot pass the major critical speed range due to the very large amplitude when the angular acceleration is less than a certain critical value.
Fig. 2Amplitude variation curves in the major critical speed with a vertical rotor
a) Unbalance within the crack side
b) Unbalance without the crack side
Different from the case of a steady-state oscillations, the whirling speed and the rotational speed are different each other and the crack opens and closes repeatedly during the passage through the major critical speed. Therefore, it is imagined that the difference in the angular position of the unbalance does not influence to the maximum amplitude in the case of non-stationary oscillations. But Fig. 3 shows that the maximum amplitude changes remarkably due to the unbalance direction. This means that the repetition of the opening and closing states do not occur frequently in the resonant range.
These results can be interpreted from the viewpoint of vibration diagnosis as follows. Since the maximum amplitude increases remarkably as in Fig. 2(a), the appearance of a crack can be detected from the incremental amplitude. On the other hand, if they are on the opposite side, it is very difficult to find it.
Fig. 3Maximum amplitudes for acceleration λ
3.2. Condition of a horizontal rotor
In this section, non-stationary oscillations during the passage through the major critical speed are investigated when the rotor system is supported horizontally. Various kinds of resonances occur in a wide rotational speed range due to a crack in view of a horizontal rotor [20].
Fig. 4Non-stationary oscillation of a horizontal rotor
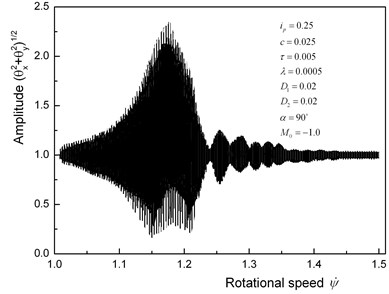
a) Time history with non-stationary
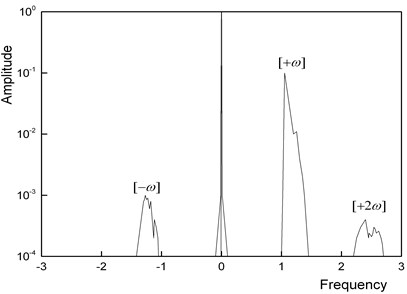
b) Spectrum with non-stationary
Time histories obtained by numerical integration are more complicated than that of a vertical rotor. A time history is shown in Fig. 4(a) for the case that the unbalance and the crack are on the same side. In addition, spectrums obtained by the complex-FFT method [20] are shown in Fig. 4(b). In Fig. 4(b), the positive abscissa represents the forward whirling motion and the negative abscissa represents the backward whirling motion. Because of the rotor passing through the unstable range, the amplitude changes remarkably. Different from a harmonic component case of a vertical rotor, many frequency components exist in the spectrum diagram. In addition to the harmonic component between 1 and 1.5, a constant component, a backward harmonic component and a forward super-harmonic component with a frequency of two times the rotational speed coexist. Therefore, it is impossible to obtain the amplitude of the harmonic component by calculating . Instead, the complex-FFT method is used to process these data.
In our previous study, based on the steady-state oscillations at the major critical speed of a cracked horizontal rotor [21], the following results were obtained: (1) in the case of the comparatively large unbalance, there exists an unstable range if the unbalance and the crack are on the same side and it disappears if they are on the opposite side; (2) in the case of the comparatively small unbalance, an unstable range appears no matter what the angular position of the unbalance. Therefore, the non-stationary oscillations are discussed with two cases in the following.
3.3. Case with a large unbalance
Fig. 5 shows amplitude variation curves with a comparatively large unbalance. The value of the unbalance is the same as that of Fig. 2 and the characteristics are almost the same for a vertical rotor. If the unbalance and the crack are on the same side, the maximum amplitudes are very large as shown in Fig. 5(a). There is no qualitative difference between a vertical rotor and a horizontal rotor as the large unbalance. Therefore, the appearance of a crack can be similarly detected only if the unbalance and the crack are on the same side. On the contrary, if they are on the opposite side, the maximum amplitudes are small as shown in Fig. 5(b).
3.4. Case with a small unbalance
Fig. 6 shows amplitude variation curves with a relatively small unbalance when the unbalance and the crack are on the opposite side. As seen from the motion equations, the cracked rotor has both characteristics of a forced vibration system owing to the unbalance and a parametrical excited system owing to the breathing mechanism of the crack and the static deflection. If the rotor is well balanced, the effect of the former diminishes then the latter appears predominantly due to the breathing of the crack and the static deflection. As the result, in the steady-state oscillation, there always exists an unstable range, no matter what the angular position of the unbalance. Therefore, the maximum amplitude of the non-stationary oscillation is large and it does not vary according to the angular position of the unbalance. Fig. 6 corresponds to Fig. 5(b). These figures indicate that the amplitude becomes large when the unbalance is not large. The results consider that, when the rotor system is well balanced, the occurrence of a crack can be monitored by the incremental amplitude to pass through the major critical speed with any directional unbalance.
Fig. 5Responses [+ω] of a horizontal rotor with a large unbalance
![Responses [+ω] of a horizontal rotor with a large unbalance](https://static-01.extrica.com/articles/18186/18186-img7.jpg)
a) Unbalance within the crack side
![Responses [+ω] of a horizontal rotor with a large unbalance](https://static-01.extrica.com/articles/18186/18186-img8.jpg)
b) Unbalance without the crack side
Fig. 6Responses [+ω] of a horizontal rotor with a small unbalance
![Responses [+ω] of a horizontal rotor with a small unbalance](https://static-01.extrica.com/articles/18186/18186-img9.jpg)
4. Forward super-harmonic and forward sub-harmonic resonances
4.1. Forward super-harmonic resonance of order 2
In the neighborhood of the rotational speed 0.52, twice the rotational speed is almost equal to a forward natural frequency and the super-harmonic resonance occurs. This resonance does not occur in a linear symmetrical rotor with a circular cross section if there is no crack.
When the rotor passes through this resonance, the amplitude changes as shown in Fig. 7. Because this super-harmonic resonance is more difficult to occur, than the harmonic resonance, comparatively large values of parameters and are used in the calculation. The maximum amplitude is almost independent to the angular position of the unbalance and does not decrease rapidly when the angular acceleration increases. These characteristics show that this kind of resonance can be used as a correct signal for the occurrence of a crack.
Fig. 7Amplitude curve of super-harmonic resonance [+2ω]
![Amplitude curve of super-harmonic resonance [+2ω]](https://static-01.extrica.com/articles/18186/18186-img10.jpg)
4.2. Forward sub-harmonic resonance of order 1/2
In the neighborhood of the rotational speed 2.23, the sub-harmonic resonance of order 1/2 occurs. This resonance does not occur in a linear symmetrical rotor if there is no crack. The amplitude variation curves are shown in Fig. 8(a) and a relationship between and is shown in Fig. 8(b). Different from the cases of the harmonic resonance and the super-harmonic resonance, the resonance curves of this steady-state oscillation bifurcate from a trivial solution with the zero amplitude. In such a case, it is known that the amplitude variation curve can change remarkably according to the initial angular displacement of the unbalance [16]. This means that the maximum amplitude takes various values for a given acceleration . As a result, the relationship between and is represented by the shaded zone in Fig. 8(b). Since this initial angular position can not be controlled generally, the maximum amplitude of a non-stationary oscillation changes randomly for every operation. In Fig. 8(b), the maximum amplitude decreases rapidly for the angular acceleration . Considering these characteristics, it is considered that this resonance is not suitable to use as a signal of the occurrence of a crack in the non-stationary oscillations because this resonance does not always occur, even if a crack exists. In order to find the occurrence of a crack by observing this resonance, it is necessary to conduct several running tests with the small angular acceleration .
Fig. 8Amplitude curve of sub-harmonic resonance [(1/2)ω]
![Amplitude curve of sub-harmonic resonance [(1/2)ω]](https://static-01.extrica.com/articles/18186/18186-img11.jpg)
a) Resonance curve
![Amplitude curve of sub-harmonic resonance [(1/2)ω]](https://static-01.extrica.com/articles/18186/18186-img12.jpg)
b) Maximum amplitude for
4.3. Comparison of characteristics of non-stationary oscillations through various resonances
As mentioned above, the characteristics of non-stationary oscillations during the passage through resonances differ depending on the kind of resonance. Here, the dependence of the maximum amplitude to the angular acceleration is summarized and compared.
Fig. 9Comparison of the relationships between rmax and λ
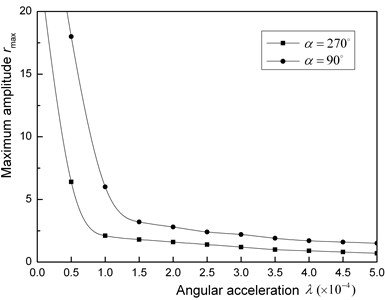
a) Major critical speed with a small unbalance
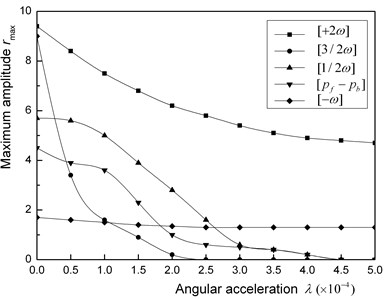
b) Various cases of sub-critical speed
Fig. 9(a) shows the case of the major critical speed of the horizontal rotor with a small unbalance. Since an unstable range exists at any directional unbalance, the maximum amplitude always becomes very large if the rotor passes through the major critical speed with a small angular acceleration. This means that, as mentioned above, the harmonic resonance can be used to detect a crack when the rotor is well balanced. When the unbalance is comparatively large (this case is not shown by a figure), the maximum amplitude to pass through the major critical speed range does not increase due to the crack if the unbalance and the crack are on the opposite side. Therefore, in this case, we must investigate the change of the maximum amplitude by changing the unbalance’s direction.
Fig. 9(b) shows the relationships between and to pass through various kinds of sub-resonances. In this figure, each plot representing the maximum amplitude is obtained by drawing response curve like Fig. 2(a). And these plots are connected smoothly by full lines. In order to investigate the quantitative difference among these sub-resonances, the same parameter values are used. Under a sub-harmonic resonance where the maximum amplitude depends on the initial angular displacement, a result for the same initial angular position is shown in this figure. From Fig. 9, the following results are confirmed: (1) if the angular acceleration is small, every kinds of resonance can be used as the signal of the occurrence of a crack; (2) if the angular acceleration is comparatively large, the super-harmonic resonance can be only used to detect a signal of the occurrence of a crack.
5. Experimental setup and results
5.1. Experimental setup
For safety, it was impossible to perform experiments on non-stationary oscillation using a horizontal rotor. Therefore, a vertical rotor system is used in experiments.
The experimental setup is shown in Fig. 10. A disk is mounted on the shaft at the positions of 200 mm or 150 mm below the middle of the elastic shaft that is simply supported using two double-row ball bearings at both shaft ends. The shaft is 700 mm in length and 12 mm in diameter. The diameter and the thickness of the disk are 481 mm and 5.5 mm, respectively. In order to make the same characteristics as in a transverse crack, a notch is made at the position 335 mm from the upper bearing and it is filled with a part of the same dimensions as the notch as shown in Fig. 10. The notch has the width 20 mm and the depth 5 mm. The phase angle in Fig. 10 represents the angle between the crack and the unbalance. The deflections in the and directions are measured by position sensors.
Fig. 10Experimental system of a vertical rotor
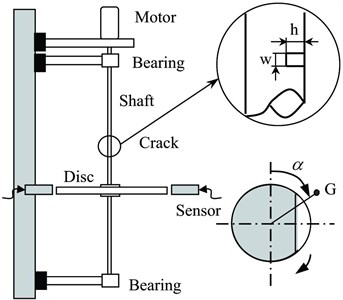
5.2. Amplitude variation during the passage through the resonance
The experimental setup where a disk is mounted on the positions of 200 mm below the middle of the elastic shaft is used.
5.2.1. Unbalance within the crack side
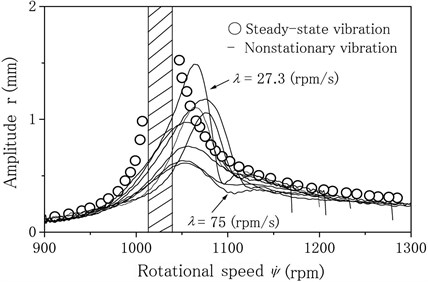
The unbalance is set 110° within the crack side. The experiments are made for eight different angular accelerations 75, 60, 50, 42.9, 37.5, 33, 30 and 27.3 rpm/s. The experimental results are represented by solid lines in Fig. 11. For comparison, the oscillation curve of the steady state response is also shown by the symbol ∘. The unstable range drawn by the hatching appears between 1015 rpm and 1040 rpm when the rotor runs with a constant speed. When the angular acceleration is 27.3 rpm/s, the maximum amplitude is large. When the angular acceleration equals 75 rpm/s, the rotor passed the unstable range with small amplitude. The experimental results shown in Fig. 11 agree qualitatively with the numerical results shown in Fig. 2(a).
Fig. 11Experimental results (unbalance within crack side)
5.2.2. Unbalance without the crack side
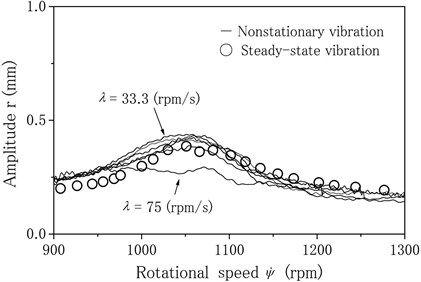
The unbalance is set 259° without the crack side. The experiments are made for six different angular accelerations 75, 60, 50, 42.9, 37.5 and 33 rpm/s. The experimental results are shown by solid lines in Fig. 12. There is not the existence of the unstable range under the steady-state oscillation. Therefore, when the rotor passes through the major critical speed, the maximum amplitude is always small. The experimental results shown in Fig. 12 agree qualitatively with the numerical results shown in Fig. 2(b).
Fig. 12Experimental results (unbalance without crack side)
5.3. Relationship with maximum amplitude and the unbalance direction
The experimental setup where a disk is mounted on the positions of 150 mm below the middle of the elastic shaft is used.
Initially, a static unbalance and a dynamic unbalance coexist in the experimental setup. Therefore, first, the rotor is balanced enough. Then, a small mass is put on the disk in order to make the unbalance of the rotor. The maximum amplitude is investigated for various directions and magnitudes of the unbalance. The experiments are made 24 times. The angular acceleration is fixed as 37.5 rpm/s. The experimental results are shown in Fig. 13. Because it is difficult to identify the direction and the magnitude of an unbalance, the phase and the amplitude of the steady-state oscillation at 850 rpm is used instead of those of unbalance. This speed is lower than the major critical speed ( 930 rpm). To eliminate the effect of the initial bending, the phases and amplitudes are compensated by taking the relative phases and amplitudes to those at the rotational speed 90 rpm.
Fig. 13Experimental statistical results (pass through the major critical speed with various cases)
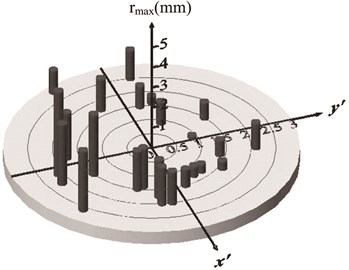
The vertical axis of Fig. 13 represents the maximum amplitude to pass through the major critical speed. The crack locates in the negative -direction. If the unbalance and the crack are on the same side (that is, ), the maximum amplitude becomes large. On the contrary, if the unbalance and the crack are on the opposite side, the maximum amplitude becomes small. Those results agree qualitatively with the numerical results shown in Figs. 2, 5 and 6. According to the above results, a crack can be detected as follows: When a crack is suspected to occur in a rotor system, a small mass is put at various positions in order to change the magnitude and the direction of an unbalance. Then, the maximum amplitude is investigated during the passage through the resonances. From the variation and the distribution of the maximum amplitude, the occurrence and the direction of a crack can be detected.
6. Conclusions
When the rotor starts-up or shuts-down, the rotational speed sweeps in a wide range under rated speed. Therefore, if some symptoms of the occurrence of a crack in non-stationary oscillations are noticed, the possibility to find a crack will increase. The paper investigated vibration characteristics to pass through a variety of resonances of a cracked rotor for detecting a crack and to avoid some defects of diagnose system with steady-state responses. The following characteristics are clarified.
1) In a vertical rotor system, the non-stationary oscillation during passages through the major critical speed depends on the unbalance direction. If the unbalance and the crack are on the same side, the maximum amplitude will increase remarkably. However, if they are on the opposite side, the maximum amplitude does not increase.
2) In view of a horizontal rotor, the characteristics are similar to that of a vertical rotor if the unbalance is relatively large. However, when the unbalance is small, the maximum amplitude changes large for any directional unbalance because an unstable range appears.
3) When the rotor passes through the critical speeds of a backward harmonic resonance and a forward super-harmonic resonance, the maximum amplitude changes large with any acceleration. In addition, based on the cases of a super-sub-harmonic resonance of order 3/2, a sub-harmonic resonance of order 1/2 and a combination resonance, the maximum amplitude decrease rapidly as the acceleration increases.
References
-
Varney P., Green I. Rotor dynamic crack diagnosis: distinguishing crack depth and location. Journal of Engineering for Gas Turbines and Power, Vol. 135, Issue 11, 2013, p. 345-355.
-
Silani M., Ziaei-Rad S., Talebi H. Vibration analysis of rotating systems with open and breathing cracks. Applied Mathematical Modelling, Vol. 37, Issue 24, 2013, p. 9907-9921.
-
Lin L., Chu F. HHT-based AE characteristics of natural fatigue cracks in rotating shafts. Mechanical Systems and Signal Processing, Vol. 26, 2012, p. 181-189.
-
Singh S. K., Tiwari R. Detection and localisation of multiple cracks in a shaft system: An experimental investigation. Measurement, Vol. 53, 2014, p. 182-193.
-
Ma H., Feng R., Pang X., et al. Effects of tooth crack on vibration responses of a profile shifted gear rotor system. Journal of Mechanical Science and Technology, Vol. 29, Issue 10, 2015, p. 4093-4104.
-
Hou L., Chen Y., Lu Z., et al. Bifurcation analysis for 2: 1 and 3: 1 super-harmonic resonances of an aircraft cracked rotor system due to maneuver load. Nonlinear Dynamics, Vol. 81, Issues 1-2, 2015, p. 531-547.
-
Sawicki J. T., Friswell M. I., Kulesza Z., et al. Detecting cracked rotors using auxiliary harmonic excitation. Journal of Sound and Vibration, Vol. 330, Issue 7, 2011, p. 1365-1381.
-
Kulesza Z. Dynamic behavior of cracked rotor subjected to multisine excitation. Journal of Sound and Vibration, Vol. 333, Issue 5, 2014, p. 1369-1378.
-
Li Y., Xu M., Wei Y., et al. A new rolling bearing fault diagnosis method based on multiscale permutation entropy and improved support vector machine based binary tree. Measurement, Vol. 77, 2016, p. 80-94.
-
Li Y., Xu M., Wei Y., et al. Health condition monitoring and early fault diagnosis of bearings using SDF and intrinsic characteristic-scale decomposition. IEEE Transactions on Instrumentation and Measurement, Vol. 65, Issue 9, 2016, p. 2174-2189.
-
Ebrahimi A., Heydari M., Behzad M. A continuous vibration theory for rotors with an open edge crack. Journal of Sound and Vibration, Vol. 333, Issue 15, 2014, p. 3522-3535.
-
Castejón C., García-Prada J. C., Gómez M. J., et al. Automatic detection of cracked rotors combining multiresolution analysis and artificial neural networks. Journal of Vibration and Control, Vol. 21, Issue 15, 2015, p. 3047-3060.
-
Ishida Y., Hirokawa K. Internal resonances of a cracked rotor: major critical speed and critical speeds in precritical range. JSME International Journal. Series C, Dynamics, Control, Robotics, Design and Manufacturing, Vol. 39, Issue 2, 1996, p. 225-233.
-
Ishida Y., Hirokawa K., Hirose M. Vibrations of a cracked rotor 3/2-order super-subharmonic and 1/2-order subharmonic resonances. Proceedings of ASME Design Engineering Technical Conferences. Vol. 3A, 1995, p. 605-612.
-
Al-Shudeifat M. A., Butcher E. A. New breathing functions for the transverse breathing crack of the cracked rotor system: approach for critical and subcritical harmonic analysis. Journal of Sound and Vibration, Vol. 330, Issue 3, 2011, p. 526-544.
-
Ishida Y., Ikeda T., Yamamoto T., et al. Nonstationary vibration of a rotating shaft with nonlinear spring characteristics during acceleration through a critical speed. A critical speed of a 1/2-order subharmonic oscillation. JSME International Journal. Series 3, Vibration, Control Engineering, Engineering for Industry, Vol. 32, Issue 4, 1989, p. 575-584.
-
Li B., Zhang C., He Z. HHT-based crack identification method for start-up rotor. Frontiers of Mechanical Engineering, Vol. 7, Issue 3, 2012, p. 300-304.
-
Li B., Zhang C. L. Hilbert-Huang transform and its application to crack identification for start-up rotor. Advances in Vibration Engineering, Vol. 12, Issue 5, 2013, p. 459-473.
-
Wang K. S., Guo D., Heyns P. S. The application of order tracking for vibration analysis of a varying speed rotor with a propagating transverse crack. Engineering Failure Analysis, Vol. 21, 2012, p. 91-101.
-
Ishid Y., Yamamoto T. Linear and Nonlinear Rotordynamics. John Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2012.
-
Ishida Y., Inoue T. Detection of a rotor crack using a harmonic excitation and nonlinear vibration analysis. Journal of Vibration and Acoustics, Vol. 128, Issue 6, 2006, p. 741-749.
About this article
This work is supported by National Natural Science Foundation of China (11402170) and by Tianjin Natural Science Foundation of China (15JCYBJC19800, 16JCZDJC30400 and 17JCZDJC38500).
