Abstract
In this paper, nonlinear vibration of Euler-Bernoulli beams resting on linear elastic foundation and subjected to the axial loads are studied analytically. Hamiltonian approach is new kind of analytical approaches are used to achieve the nonlinear frequency of the problem. The nonlinear vibration equation is also solved numerically using Runge-Kutta 4th technique. Comparison of Hamiltonian approach (HA) with Runge-Kutta 4th leads to highly accurate solutions using Hamiltonian approach.
1. Introduction
In the past few decades many researchers have been working on the nonlinear vibration equations of beams resting on elastic foundations. Many different approaches have been used to modeling the soil such as Winkler, Pasternak or Vlasov, Flonenko-Borodich foundations. Winkler approach is a linear algebraic relationship is introduces between the normal displacement of the structure and the contact pressure [1]. A set of mutually parallel independent spring elements are used in the Winkler model to represent the soil medium [2]. Therefore, analyzing the nonlinear behavior of the system could be more easily compared to other methods [3]. Many researchers have been worked on the Winkler elastic foundation modeling in the past few decades [4-6]. Generally, finding an exact solution for nonlinear problems are very difficult, therefore some approximate analytical methods have been proposed by many researchers to solve nonlinear vibration problems such as: Parameter Expansion Method [7], Variational iteration Method [8], Homotopy Perturbation Method [9], Max-Min Approach [10, 11] and other analytical techniques [12-15]. In this study, Hamiltonian approach is applied to solve the nonlinear vibration equation of Euler-Bernoulli beam resting on a Winkler elastic foundation.
2. Description of the problem
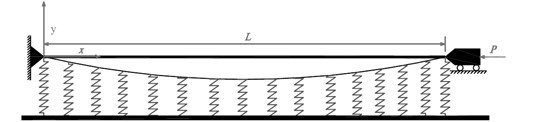
Fig. 1 represents a simply-supported buckled Euler-Bernoulli beam fixed at one end resting on Winkler foundation. The basic assumptions of the beam theory are considered such as [4]:
– The beam is isotropic and elastic;
– The beam deformation is dominated by bending and the distribution and rotation are negligible;
– The beam is along as slender with a constant section along the axis.
The equation of motion for an axially loaded Euler-Bernoulli beam by considering the mid-plane stretching effect is:
where is a foundation modulus and is a distributed load in the transverse direction.
Assume the non-conservative forces were equal to zero. Therefore Eq. (1) can be written as follows:
Here we introduce the following non-dimensional variables:
where is the radius of gyration of the cross-section. We assume the elastic coefficient of Winkler foundation is constant . Then Eq. (2) can be written as follows:
If we assume in which is an unknown time dependent function and is a trial function which must satisfy the kinematic boundary conditions and using the Galerkin method, then we will have the following governing nonlinear vibration equation of motion for an axially loaded Euler-Bernoulli beam:
The initial conditions for center of the beam are:
The value of the , and can be obtained as follow:
Fig. 1Schematic representation of an axially loaded Euler-Bernoulli beam resting on Winkler foundation
3. Basic idea of He’s Hamiltonian approach
The Hamiltonian Approach is a novel method which was proposed by He [15]. The Hamiltonian Approach is one of the simple and effective approaches for conservative oscillatory systems. Here we give an introduction of this approach:
With initial conditions:
The variation principle for the Eq. (8) can be obtained easily by using the semi-inverse method [15]:
where is period of the nonlinear oscillator, .
The first term of Eq. (10), is kinetic energy and is the potential energy, so the Eq. (10) is the least Lagrangian action, from which we can obtain its Hamiltonian, which reads:
From Eq. (11), we have:
Introducing a new function, , defined as:
Eq. (12) is, then, equivalent to the following one:
Or:
From Eq. (15) we can obtain approximate frequency-amplitude relationship of a nonlinear oscillator.
4. Solution using Hamiltonian approach
The Hamiltonian of Eq. (5) is constructed as:
Integrating Eq. (16) with respect to t from 0 to , we have:
We use the following trial function:
If we Substitute Eq. (18) into Eq. (17), its results are:
Setting:
If we solve Eq. (20) the approximate frequency of the system is:
Hence, the approximate solution can be readily obtained:
The ration of the non-linear to linear frequency is:
5. Results and discussion
The Hamiltonian approach (HA) is used to obtain an analytical solution for simply supported beam at constant elastic modulus. To obtain numerical solution we must specify the parameter . This parameter depends on value of , , and , then we have:
So Eq. (21) become:
For simply supported beam the trial function is assumed.
Table 1Comparison of nonlinear to linear frequency ratio (ωNL/ωL) for Simply-Supported Beams
Present Study (HA) | Pade approximate [12] | Pade approximate [12] | ||
0.2 | 3 | 1.04403 | 1.04388 | 1.04388 |
0.6 | 3 | 1.34536 | 1.33973 | 1.33970 |
1 | 3 | 1.80277 | 1.78468 | 1.78442 |
1.5 | 3 | 2.46221 | 2.42618 | 2.42541 |
2 | 3 | 3.16227 | 3.10845 | 3.10712 |
2.5 | 3 | 3.88104 | 3.80991 | 3.80802 |
3 | 3 | 4.60977 | 4.52172 | 4.51927 |
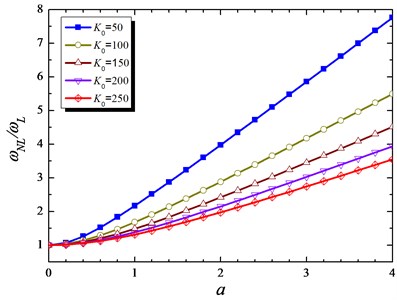
Table 1 represents the comparison of present study with the results obtained by [12] for different values of amplitude and . Fig. 2 considered the comparisons of Hamiltonian approach and Runge-Kutta algorithm to show the effects of the elastic soil stiffness on the displacement response. Fig. 3 is one of the important results in this section; because it is shown the effects of on ration the nonlinear to linear frequency of the beam vibration. It can be observed from the figure when the stiffness of the elastic soil grows up; the linear and nonlinear frequency comes to be closer and the ratio is also closer to 1.
Fig. 2Comparison of analytical solution of time history response with the numerical solution for simply supported beam a= 0.3, p= 10, K0= 100
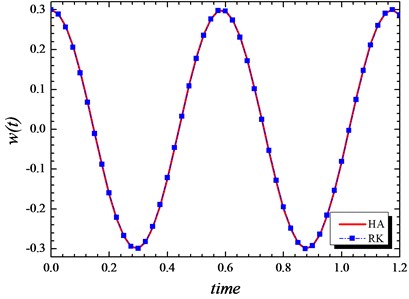
Fig. 3Influence of K0 on nonlinear to linear frequency base on amplitude for p= 10
6. Conclusions
A new application of Hamiltonian approach has been presented to solve nonlinear response of a Euler-Bernoulli beam resting on a Winkler elastic foundation and subjected to the axial loads. Winkler approach is used widely to the beams and pipelines resting on an elastic soil. The results of Hamiltonian approach compared with numerical solutions using Runge-Kutta’s algorithm. This paper indicated that the Hamiltonian approach can be extending easily to other conservative nonlinear problems.
References
-
Gorbunov-Posadov M. I., Malikova T.A., et al. The Design of Structures on an Elastic Foundation. Stroiizdat, Moscow, 1973.
-
Al-Hosani K., Fadhil S., El-Zafrany A. Fundamental solution and boundary element analysis of thick plates on Winkler foundation. Computers and Structures, Vol. 70, Issue 3, 1999, p. 325-336.
-
Soldatos K., Selvadurai A. Flexure of beams resting on hyperbolic elastic foundations. International Journal of Solids and Structures, Vol. 21, Issue 4, 1985, p. 373-388.
-
Zhou D. A general solution to vibrations of beams on variable Winkler elastic foundation. Computers and Structures, Vol. 47, Issue 1, 1993, p. 83-90.
-
Auersch L. Dynamic interaction of various beams with the underlying soil-finite and infinite, half-space and Winkler models. European Journal of Mechanics – A/Solids, Vol. 27, Issue 5, 2008, p. 933-958.
-
Eisenberger M., Clastornik J. Vibrations and buckling of a beam on a variable Winkler elastic foundation. Journal of Sound and Vibration, Vol. 115, Issue 2, 1987, p. 233-241.
-
Xu L. He’s parameter-expanding methods for strongly nonlinear oscillators. Journal of Computational and Applied Mathematics, Vol. 207, Issue 1, 2007, p. 148-154.
-
Liu Y., Gurram C. S. The use of He’s variational iteration method for obtaining the free vibration of a Euler-Bernoulli beam. Mathematical and Computer Modelling, Vol. 50, Issues 11-12, 2009, p. 1545-1552.
-
Shou D. H. The homotopy perturbation method for nonlinear oscillators. Computers and Mathematics with Applications, Vol. 58, Issues 11-12, 2009, p. 2456-2459.
-
Bayat M., Pakar I., Domaiirry G. Recent developments of some asymptotic methods and their applications for nonlinear vibration equations in engineering problems: a review. Latin American Journal of Solids and Structures, Vol. 9, Issue 2, 2012, p. 145-234.
-
He J. H. Max-min approach to nonlinear oscillators. International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 9, Issue 2, 2008, p. 207-210.
-
Azrar L., Benamar R., White R. A semi-analytical approach to the non-linear dynamic response problem of S-S and C-C beams at large vibration amplitudes. Part I: General theory and application to the single mode approach to free and forced vibration analysis. Journal of Sound and Vibration, Vol. 224, Issue 2, 1999, p. 183-207.
-
He J. H. Preliminary report on the energy balance for nonlinear oscillations. Mechanics Research Communications, Vol. 29, Issues 2-3, 2002, p. 107-111.
-
Bayat M., Pakar I. On the large amplitude free vibrations of axially loaded Euler-Bernoulli beams. Steel and Composite Structures, Vol. 14, Issue 1, 2013, p. 73-83.
-
He J. H. Hamiltonian approach to nonlinear oscillators. Physics Letters A, Vol. 374, Issue 23, 2010, p. 2312-2314.
