Abstract
The distribution state evolution of concrete cracking evolution energy has been discussed in which with dissipative system characteristics is considered, and combined the theory of information entropy with energy method. The function of entropy evolution change for in different stage of crack stable and unstable propagations evolution is established. The element damage extent formula is deduced, which can be applied to judge the stage of crack. Finally, the cracking process of double span continuous beam is simulated by Midas/FEA to compare with other literature. The result shows that the strain energy entropy function proposed can is be capable of well describing the evolution law of concrete cracking evolution.
1. Introduction
Entropy was proposed by German famous physicist Clausius in 1865, which is a special parameter in thermodynamics and statistical physics. As a state variable, the change of entropy was related to the dispersion of matter [1], and the macroscopic significance indicates the uniform degree of the energy distribution of the system. In an isolated system, the occurrence of any irreversible process will lead to the rising of entropy [2]. At present, for non-reversible process, it always goes along a single direction of entropy increasing and eventually reaches equilibrium while entropy reaches maximum [3-5].
In recent years, the research of concrete crack expansion was caused great concern in civil engineering. The discrete crack model and distribution crack model are coupled by Wells G. N. to simulate the crack evolution which includes micro-cracking, crack propagation and final destruction for a unilateral cut concrete specimens [6, 7]. The fracture theory and analysis method of concrete crack development are established by Shi-lang Xu and Yan-hua Zhao, the double-K fracture criterion was proposed according to experimental result [12]. The concrete crack propagation with the perspective of energy distribution was analyzed by Pei-jiang Cong and Chong-shi Gu [2]. However, double-K fracture criterion proceeding from the linear elastic fracture mechanics and the study stage of strain energy entropy still remains on identification of crack initiation and stable growth. In this paper, crack evolution function based on entropy was proposed in the different stage of craching propagation, and the whole entropy change processing of concrete crack is studied based on information entropy and energy method to prove the validity of the formula.
2. Theory of information entropy
The strain energy of unit by the finite element theory [9]:
where, is the strain energy of unit ; – the number of unit integration points; – the stress vector; – the elastic strain vector; – the volume of unit integration point ; – plastic strain energy of units. Then the total strain energy is shown as following:
where, is the number of units. Set:
The information entropy function of the structure is defined as:
where, is a constant coefficient, and set as 1.0 in engineering.
3. Crack evolution function based on entropy
3.1. Crack initiation and stable growth stage
Based on the finite element theory and the characteristic of dissipative system [2], the change of strain entropy can be described by Eq. (6) as following:
where, – the original entropy of structure; – strain energy entropy of structure for the th step; – strain energy of unit for the th step. The structural entropy difference of strain energy at different load step is obtained by Eq. (5). When 0, there is no damage in structure; When 0, damage occurs.
3.2. Failure stage
3.2.1. Energy consumption of fracture zone
When the external load reaches its maximum , crack will expand rapidly. According to softening distribution cohesion model on the fracture zone [11], the work that cohesion act on unit area at the critical state of instability is [13]:
where, – the horizontal distance between any point and the crack gap at fracture zone; is the initial length of the gap; – the critically instable length; the fracture energy at , that is the absorbed energy when the gap of crack increases from 0 to .
3.2.2. Entropy function establishment of failure stage
According to the principle of conservation of energy, the energy balance equation is:
where, – the total energy of structure; – strain energy of structure.
is described as the entropy of unit before structure being disturbed. According to the Eq. (6), the fracture criterion of crack is established:
where, – the structural strain energy entropy for disturbed structure. When 0, the unit of structure is not disturbed (no cracking). When 0, the damage extent is defined as:
Judge further whether the unit is invalid according to the literature [8, 14, 15]. Using the literature [8] and Eq. (9) to determine the number of destructive units Num. Then structural strain energy of unit for the th step can be obtained after the crack appearing, the Eq. (7) can be further expressed:
where, – the strain energy of unit for the th step after crack appearing; – strain energy of structure for the th step.
3.3. Numerical calculation
A concrete beam model is established by Midas/FEA to analyze crack evolution. Stress-strain data is extracted to calculate strain energy of unit which can be used to judge whether unit damaged or not. If damaged, the unit will be eliminated in coming analysis. Meanwhile, the fracture energy is calculated. Then the strain energy of structure should be recalculated for the shorten FE model, and the strain energy entropy will be obtained by Eq. (11), correspondingly. Fig. 1 shows the specific process.
4. Numerical computation
4.1. Numerical model
A two-equal-span continuous concrete beam model is established by Midas/FEA. Each span is 1000 mm, and cross-section size is 400 mm×200 mm, and the strength of concrete is C50. The surface load area at the first mid-span is 400 mm×10 mm and the load intensity is 20 N/mm2 (Fig. 2). The system automatically load steps by Midas/FEA is applied for analysis and control, and the initial load factor is 0.01. Material properties are shown in Table 1.
There are two major cracks at first mid-span and mid-support (Fig. 3) by running the nonlinear analysis module of cracking of Midas/FEA. And while load increasing, the crack evolution at the first mid-span will contain crack initiation, stable growth, unstable propagation and failure stage.
Fig. 1The chart of entropy function numerical computation
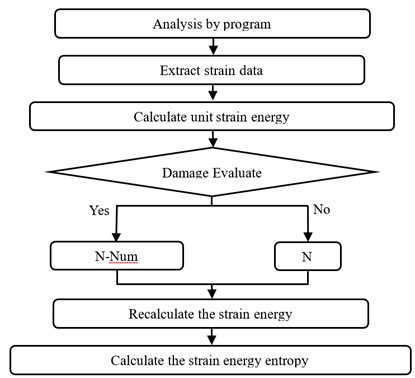
Fig. 2Midas/FEA beam model
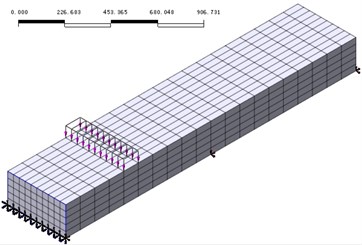
Table 1Material properties
Elastic modulus (N/mm2) | Poisson’s ratio | Weight density (N/mm3) | Influence of transverse crack | Constraint effect |
34965 | 0.167 | 2.5×10-5 | Vecchio Collins | Selby vecchio |
Fig. 3Crack state: a) at first middle span, b) at middle support
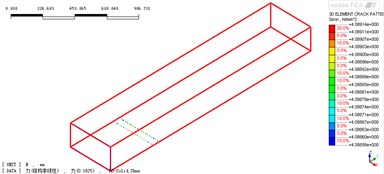
a)
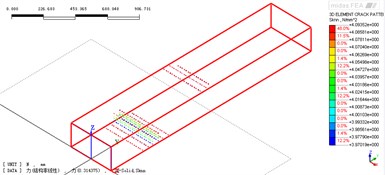
b)
4.2. Calculation of crack evolution entropy
4.2.1. Entropy changes of first crack initiation and stable growth
The structure strain energy entropy of every step is calculated, and entropy difference of strain energy can be obtained by initial value and current one (Table 2). Table 2 shows when incremental step is between 1 and 7, 0, which means the structure is undamaged, while at 8th increment step, first crack appears and entropy difference of strain energy continues to increase.
The unit entropy difference at the first mid-span is calculated, the curve of step and entropy difference is drawn in Fig. 4. From the curve, at 8th step, the entropy difference is changing, which means crack appears, this conclusion is consistent with integral analysis result in Table 2. While till 19th step, entropy difference of strain energy is stable growth, which means that this crack is under stable extending. The 19th step is instable point of cracking.
Table 2Change for load-entropy incremental step
No. | Load factor | Strain energy entropy (J) | Entropy difference () | No. | Load factor | Strain energy entropy (J) | Entropy difference () |
1 | 0.010000 | 5.989 | 0 | 11 | 0.314375 | 6.051 | 0.062 |
2 | 0.020000 | 5.989 | 0 | 12 | 0.352344 | 6.075 | 0.086 |
3 | 0.035000 | 5.989 | 0 | 13 | 0.390312 | 6.094 | 0.105 |
4 | 0.050000 | 5.989 | 0 | 14 | 0.428281 | 6.117 | 0.128 |
5 | 0.072500 | 5.989 | 0 | 15 | 0.466250 | 6.138 | 0.149 |
6 | 0.095000 | 5.989 | 0 | 16 | 0.504219 | 6.159 | 0.170 |
7 | 0.128750 | 5.989 | 0 | 17 | 0.542188 | 6.179 | 0.190 |
8 | 0.162500 | 5.991 | 0.002 | 18 | 0.580156 | 6.201 | 0.212 |
9 | 0.213125 | 6.002 | 0.013 | 19 | 0.618125 | 6.222 | 0.233 |
10 | 0.263750 | 6.024 | 0.035 | 20 | 0.656094 | 6.239 | 0.250 |
4.2.2. Entropy changing of second crack initiation
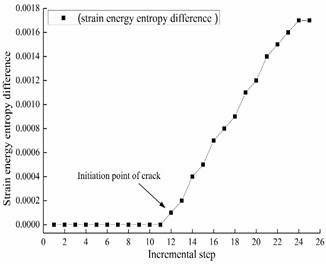
Mid-support stress-strain data is extracted and the element strain energy is solved to calculate entropy difference, the result is drawn in Fig. 5. The mid-support appears new crack and entropy difference of strain energy is nonzero when loading to the 12th increment step (Fig. 4).
Fig. 4Strain energy entropy difference at the first mid-span
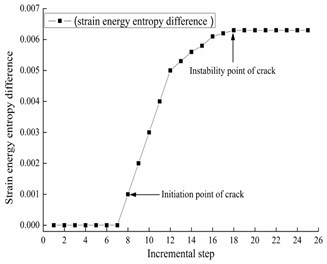
Fig. 5Strain energy entropy difference for mid-span
4.2.3. Entropy changing of failure stage
When up to the 19th increment step, the first crack shows unstable state. After determining the number of invalid unit, the strain energy of structure is recalculated to obtain the entropy for failure stage. At the same time, entropy changing with calculation method proposed by the literature [2] (Table 3) is compared with Table 2, the comparison curve is drawn in Fig. 6.
The data of this paper indicates that strain energy entropy decreases at first and then increase when incremental step from 20 up to 25. It is due to the instability of crack at first mid-span and energy redistribution happening. Part of energy is consumed by the development of new crack.
Strain energy entropy function is a convex function defined on a convex set, however, according to the data of the literature [2], strain energy entropy will be continually increasing after first crack appearing. Therefore, the data here is more accurate.
According to above analysis, the rule of crack evolution is as following: the strain energy entropy remains stable before crack appearing, and starts to increase after crack appearing, then reaches instable point of cracking, and decreases at first then rises until concrete failure.
5. Conclusions
Firstly, a brief review about basic theory of entropy is introduced, and then the strain energy entropy is proposed based on dissipative system and energy method, which being considered with the internal energy distribution. The changing of entropy is studied under the whole concrete crack evolution stage. The results show that:
1) Strain energy entropy function is a convex function. Therefore, the data in this paper is more accurate by being compared with that of the literature [2].
2) The crack initiation, stable growth, unstable propagation and failure stage can be described by the whole curve of strain energy entropy changing, which is proved more comprehensive by the numerical simulation of continuous beam.
3) The new thought based on whole curve of strain energy entropy changing, can offer a new method to research concrete cracking evolution.
Fig. 6Strain energy entropy for crack evolution’s comparison figure
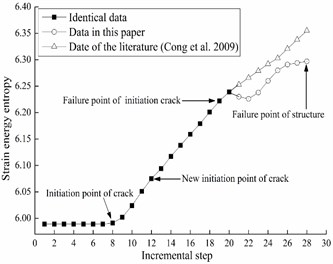
Table 3Entropy changing for instable stage incremental step
Load factor | Strain energy entropy (J) | Data of the literature (Cong et al. 2009) | |
21 | 0.694062 | 6.230 | 6.253 |
22 | 0.732031 | 6.226 | 6.266 |
23 | 0.770000 | 6.238 | 6.279 |
24 | 0.807969 | 6.260 | 6.292 |
25 | 0.845937 | 6.280 | 6.303 |
26 | 0.883906 | 6.291 | 6.321 |
27 | 0.921875 | 6.294 | 6.338 |
28 | 0.959844 | 6.297 | 6.355 |
References
-
Chen J. J., Cao Y. B., Duan B. Y. Structure principle of information entropy and maximum entropy. Chinese Journal of Applied Mechanics, Vol. 15, Issue 4, 1998, p. 116-121.
-
Cong P. J., Gu C. S., Wang J. Application of entropy theory in the analysis of concrete crack propagation process. Journal of Basic Science and Engineering, Vol. 16, Issue 1, 2009, p. 50-56.
-
Guo H. Y., Li Z. L. Structural damage identification based on bayesian theory and improved immune genetic algorithm. Expert Systems with Applications, Vol. 39, Issue 7, 2012, p. 6426-6434.
-
Hsu T. Y., Loh C. H. Damage diagnosis of frame structures using modified modal strain energy change method. Journal of Engineering Mechanics, Vol. 134, Issue 11, 2008, p. 1000-1012.
-
Li R. S. Non-Equilibrium Thermodynamics and Dissipative Structure. Tsinghua University Press, Beijing, 1986.
-
Liu G. H., Wu Z. G. New thought on dynamic identification technology for damage detection of RC structure by introducing information entropy theory. Journal of Vibration and Shock, Vol. 30, Issue 6, 2011, p. 162-171.
-
Shannon C. E. A mathematical theory of communication. Bell System Technical Journal, Vol. 27, 1948, p. 623-656.
-
Sun Z. G., Gao Z. M., Ni Y. Q. Identification of damaged members and damage extent in bridge deck by neural network. Engineering Mechanics, Vol. 23, Issue 2, 2006, p. 18-22.
-
Tang S. Y. A Mystery of the World’s Resolve. China University of Technology Press, Hefei, 2004.
-
Wells G. N., Sluys L. J., De B., St R. Simulating the propagation of displacement discontinuities in a regularized strain-sotening medium. International Journal for Numerical Methods in Engineering, Vol. 53, Issue 5, 2002, p. 1235-1256.
-
Wright H. T., Odyemi H. R., et al. The experimental behavior of double skin composite elements. Journal of Constructional Steel Research, Vol. 19, Issue 2, 1991, p. 97-110.
-
Xu S. L., Zhao Y. H. A dual-G criterion for crack propagation in concrete structures. China Civil Engineering Journal, Vol. 37, Issue 10, 2004, p. 13-18.
-
Xu S. L., Zhao Y. H. Analysis and criterion of fracture process for crack propagation in concrete. Engineering Mechanics Vol. 25, 2008, p. 20-33.
-
Xu W. Research and expansion of information entropy’s incremental property. Telecom World, Vol. 4, 2016, p. 212-213.
-
Zhao C. Y. Research on the Law of Hydraulic Fracture Propagation Based on Entropy Theory. Northeast Petroleum University, Daqing, 2011.
