Abstract
According to time-temperature superposition (TTS) and WLF formula, the temperature-dependent and frequency-dependent kinetic parameters of the railpads of WJ-7 fasteners were predicted based on the experimental results at a certain frequency and under the different temperatures. By combining the pseudo excitation method and symplectic mathematics scheme, the impact of railpads frequency-dependent and temperature-dependent stiffness on the random variation of the coupled vehicle-track system was investigated efficiently. The results suggest that, within the range of environment temperature and frequency-dependent extent of railpads in the railway, the PSD peak of the vertical random vibration acceleration of the wheelsets and rail gets the largest increase of 3.3 times at least, and the increment of their 1st dominant frequency also reaches up to 20.6 Hz or more. Therefore, in order to accurately analyze the random vibration responses of the vehicle-track coupled system, experiments must be conducted to obtain the accurate kinetic parameters of the polymer materials like railpads.
1. Introduction
When the vehicles are moving on the track, the track irregularity will directly acts on the vehicle and track structure, arouse their respective vibration and directly affect the safety, ride comfort, fatigue and noise of the vehicle and the line. Therefore, the random vibration analysis of vehicle and track structure, especially the calculation of the power spectrum density (PSD) of their dynamic response, plays a very important role in the calculation of railway transportation dynamics.
In 1992, Zhai Wan-ming [1]firstly explored the vehicle and track structure as a whole system and established the vertical vehicle-track unified model by adopting the system engineering approach, laying a foundation for the vehicle-track coupled system dynamics. Later, Popp [2] and Dumitriu [3] together with many other scholars conducted more in-depth studies on this model, contributing to its wide recognition and rapid development. Thus, the vehicle-track coupled system dynamics also became a new research field to be explored.
The difficulties for the random vibration analysis of the vehicle-track coupled system mainly lie in the large degree of freedom of the structure and the low computational efficiency of the traditional random vibration analysis method. When the finite element method is adopted to establish a finite-length track model, the track structure should include the length of dozens of sleepers at the front and back of the vehicle to basically eliminate the impact of the track boundary conditions. Thus, the random vibration analysis for a track model with such a large degree of freedom will require an unbearable computational effort.
As a continuous periodic support structure, the track structure can be regarded as a typical periodic chain structure. In the earlier time, the scholars carried out a fundamental research on the vibration characteristics of the periodic structure, which laid a solid foundation for the calculation of the dynamic response of the periodic structure. The calculation of the steady-state response for periodic chain structure under the waves’ free propagation and harmonic loading is becoming more and more mature, and the commonly used calculation methods include transfer matrix method [4], transformation method [5], wave vector method [6], spectral finite element method [7], substructure iteration method [8], etc. Among them, the symplectic mathematical method [9, 10] is successfully applied, providing an accurate and efficient calculation solution to the dynamic response of infinitely periodic chain structure under harmonic loading. Based on this, Lin Jia-hao combined the pseudo excitation method [11, 12] with the symplectic mathematical scheme and solved the random dynamic response PSD of infinitely periodic chain structure under stationary/non-stationary random excitation. LV Feng [13] et al. further applied these results in the random vibration analysis of the vehicle-track coupled system.
Based on the research results of the above methods, the pseudo excitation method and the symplectic mathematical scheme are adopted to establish a model and find the solution to random vibration of the vehicle-track coupled system, and the accuracy and efficiency of the calculations are greatly improved. However, the frequency domain calculation results for the algorithms are not so satisfactory, which is possibly attributed to the problem of calculation parameters. Generally, the dynamic parameters of track pads (such as rail pads, under sleeper pads and bed pads) are just regarded as a constant in the above-mentioned models. However, the dynamic mechanical parameters of high polymer track pads actually have a close correlation with environment temperatures, exciting frequencies and exciting amplitudes [14-16]. Squicciarini et al. [17] performed a field measurement of the noise from passing trains at temperature of 0-+35 °C. The test results show that there an increase of 3-4 dB. Smutny [18] performed some laboratory measurements of dynamic parameters of a single rail fastening by mechanical shock simulated with a hammer. Lin et al. [19] showed a simple experimental method to evaluate the frequency-dependent rubber mount stiffness and damping characteristics by utilizing the measured complex frequency response function from impact test and by least-squares polynomial curve fitting the data obtained from the test. Oregui et al. [20] proposed combining dynamic mechanical analysis and the time-temperature superposition principle to determine various railpad dynamic properties. Yet, the frequency-dependent and temperature-dependent features of dynamics parameters of these polymer damping materials are rarely taken into account in the dynamic analysis of the vehicle-track coupled system; instead, values are determined just in accordance with the measured dynamic stiffness values under the 3-5 Hz vibration conditions. Obviously, such simplification is not reasonable.
Thus, with the indispensable railpad in the railway traffic as the research object, the symplectic mathematical scheme and pseudo-excitation method are adopted for infinitely periodic substructure to establish a vehicle-track coupled model. The model was used to study the impact of railpads frequency-dependent and temperature-dependent stiffness on the random variation acceleration of the vehicle body, bogie, wheels and steel rail. Further, within the range of environment temperature and the frequency-dependent extent of the railpads of WJ-7 fastener, the change rules of random vibration response of the coupled vehicle-track system are discussed in frequency domain.
2. The symplectic analysis model for vertical random variation of the coupled vehicle-track system
Taking the type-B metro vehicle and the embedded sleeper ballastless track as objects, the pseudo-excitation method [11] and symplectic mathematical scheme [9] are adopted to establish the symplectic model for vertical random vibration of the vehicle-tack coupled system.
2.1. Equation of motion of the vehicle
The metro vehicle can be modeled as a half-car system with two suspensions moving on the track. It can effectively reflect the ups and downs and nod movement of the vehicle body and front-and-rear bogies, as well as the vertical movements of four wheel sets, including 10 degrees of freedom (see Fig. 1).
Fig. 1Schematic drawings of the model of vehicle
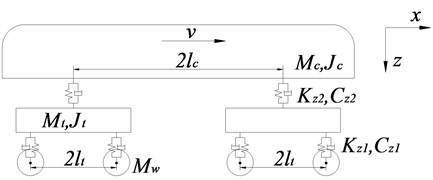
In the Fig. 1, , and are the mass of vehicle body, bogie and wheel set; and are the rotational inertia of vehicle body and bogie; and are the stiffness of the first and second suspension systems, and and are the damping of the first and second suspension systems respectively; is half of the distance between two axles of same bogie; is half of the distance between two bogie centers; and v is the vehicle speed.
Therefore, it can be seen that the equation of motion (Eq. (1)) of the vehicle under the steady-state harmonic excitation is expressed as:
In Eq. (1), , , are the stiffness matrix, damping matrix and mass matrix of the vehicle (see Table 1), respectively; is the displacement vectors of the vehicle, is the dynamic stiffness matrix of the vehicle, and is the load vector of the wheel-rail force.
2.2. Equation of motion of the track
The embedded sleeper track is the most common metro track, which can also be approximated as an infinite periodic structure (as shown in Fig. 2). Therefore, the symplectic mathematical scheme can be adopted to establish the equations of motion of the track. Where , is the bending stiffness and weight per meter of the rail, and , is the railpad stiffness and damping.
Fig. 2Schematic drawings of vertical whole structure and substructure of embedded sleeper tracks
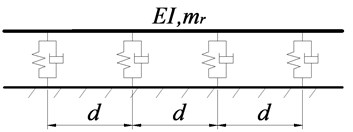
a) Whole structure
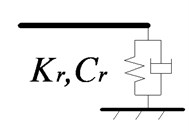
b) Substructure
2.2.1. Symplectic mathematical scheme of infinite periodic chain substructure [9]
The infinite periodic chain substructure is shown as Fig. 3.
It includes the substructure sub* under the external load and the substructure sub without external load. When the substructure sub* is under a harmonic load with a specific circular frequency of , its equations of motion can be arranged as below:
where , and are the displacement vectors at the left- and right-hand interfaces and is the internal displacement vector and; , and are the corresponding nodal force vectors; where , and are the external harmonic load vectors; et al. are the nine sub-blocks of the dynamic stiffness matrix.
Fig. 3Schematic drawing of infinite periodic chain structures
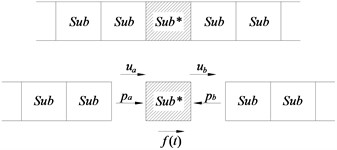
For non-loaded substructure, the internal degree of freedom in Eq. (2) can be eliminated and the following equation can thus be obtained:
where and . Thus, Eq. (2) can be further transformed into a form of state space vector:
where is the wave propagation transformation matrix. is the propagation coefficient and eigenvalues of , and so is 1/. In addition, is defined as the corresponding eigenvector. Therefore, 2 eigenvectors can constitute the following matrix equation:
and are the dynamic stiffness matrixes of the left- and right-hand interfaces of the substructure, which can be obtained from the characteristic vector matrix :
The degrees of freedom and in Eq. (2) be expressed in mode space as:
where and are coefficient vectors. By eliminating the internal degree of freedom in Eq. (2), the equation about the undetermined coefficients and can be expressed as below:
where , , , and ; in addition, , and .
After getting the vectors and through the above equation, the required responses , at the th interface of the periodic structure can be obtained in accordance with Eq. (9):
where the subscripts and of , mean the left- and right-hand interfaces of the substructure; positive is to the right of the loaded substructure and negative is to its left, with the zeroth interface being between the loaded substructure and the one to its right for and to its left for .
2.2.2. The symplectic model of embedded long sleeper ballastless track
The track is regarded as a periodic structure in which the substructure consists of the pair of rails between neighboring sleepers, and the pair of rails is represented by a single Bernoulli-Euler beam.
The track has four degrees of freedom, including the vertical and rotational degrees of freedom (, , and ) at each of its two interfaces of the beam. When the track subjected to steady-state harmonic excitation, its equation of motion is expressed as:
where , , are the stiffness matrix, damping matrix and mass matrix of the track; is the displacement response of the th substructure; is the dynamic stiffness matrix of the substructure; are the corresponding nodal force vectors; is the wheel-rail force; is the shape function column vector of the Bernoulli-Euler beam element.
Then, Eq. (10) can be expressed as:
Thus, the displacements of the left- and right-hand interfaces of the th substructure caused by the wheel-rail force can be obtained through Eq. (10), as shown below:
where represents the number of interfaces between the center of the th substructure and the th interaction force and; suggests the right substructure and represents the left substructure; and are the displacements of the left- and right-hand interfaces at the th contact position, respectively.
2.3. Vehicle-track vertical coupled relations
Assuming that the vehicle and the track are connected through linear Hertz contact spring [21], the wheel-rail force can be thus expressed as:
where is the displacement of the rail at the th wheel-rail contact point, is the pseudo track irregularity, is the displacement of the th wheel set.
For a single carriage, there are four contact points between wheel and rail. The left- and right-hand displacement vectors of the th substructure, and , can be obtained as the sum of the responses caused by each of the four wheel-rail forces, i.e.:
Consequently, the displacement of the rail at the contact point is expressed as:
Further, the equation of motion of the coupled vehicle-track system can be obtained:
where is the dynamic stiffness matrix of the coupled system, , and is the pseudo force vector.
2.4. Pseudo-excitation method for random vibration of the vehicle-track coupled system
Pseudo-excitation method is an accurate and efficient random vibration analysis method. The stationary random vibration analysis can be equivalent to the harmonic vibration analysis.
(a) ,
(b) ,
(c) .
Basic principle of pseudo-excitation method is shown in Fig. 4. According to the traditional random vibration theories, when the linear system is subjected to the single-point stationary random excitation of the PSD , the response PSD of the system is shown in Fig. 4(a); if the system is subjected to the unit harmonic load , its corresponding response will be shown in Fig. 4(b); According to the nature of linear system, if is multiplied by the unit harmonic load , its response should also be multiplied by , as shown in Fig. 4(c). Thus, the pseudo excitation can be constructed, and the pseudo response can be obtained. In this way, the response PSD can be acquired by multiplying pseudo response with its complex conjugate:
Based on the pseudo-excitation method, we can know that if the PSD of the track irregularity is known, the pseudo-excitation vectors of the single carriage at the four vehicle-track contact points can be constructed:
where , , and ; is the vehicle speed. After the pseudo-excitation is introduced, the pseudo force vector of the vehicle-track coupled system can be expressed as:
Thus, the pseudo response of the vehicle-track coupled system can be obtained, and the PSD of the response can be solved by means of Eq. (17).
3. Impact of the rail pads frequency-dependent stiffness on random vibration of the vehicle-track coupled system
3.1. The main calculation parameters
By using the above symplectic model established for the random vibration of the vehicle-track coupled system,taking the type-B metro vehicle running on the embedded sleeper ballast less track with the American fifth-grade vertical irregularity PSD (with a wavelength longer than 1 m) and the track irregularity PSD of Chinese Shi-tai line (with a wavelength less than 1 m) at the speed of 80 km/h as a subject for study, the impact of the frequency-dependent stiffness of rail pads on the vertical random vibration response of the vehicle body, bogie, wheels and rail in frequency domain is explored. The calculation parameters of the type-B metro vehicle and the embedded sleeper ballast less track are shown in Table 1 and Table 2.
Table 1Parameters of type-B metro vehicle
Parameters | Values | Parameters | Values |
Vehicle body mass, | 21.92 t | Primary suspension damping | 5 kN·s/m |
Wheelset mass, | 1.42 t | Secondary suspension stiffness | 275 kN·m-1 |
Bogie mass, | 2.55 t | Secondary suspension damping | 30 kN·s/m |
Vehicle body inertia, | 617.31 t·m2 | Bogie spacing, | 12.6 m |
Bogie inertia, | 1.75 t·m2 | Wheelset spacing, | 2.2 m |
Primary suspension stiffness | 1700 kN·m-1 | Contact constant, | 5.2e-8 m/N2/3 |
Table 2Parameters of track model
Track parts | Parameters | Values |
Rail | Bending stiffness, EI | 6.62×106 N·m2 |
Linear density, | 60.64 kg/m | |
Fastener system | Rail pad stiffness / | 50 kN/mm |
Rail pad damping / | 5.0×104 kN·s/m | |
Sleeper spacing, | 0.6m |
3.2. The measurement and prediction of the dynamic mechanical performances of rail pads
As far as most of high polymer materials are concerned, the similar dynamic mechanical performances can be observed at low temperatures or high frequencies. According to Time-Temperature Superposition (TTS) and WLF formula, the temperature-dependent and frequency-dependent dynamic mechanical parameters of rail pads can be predicted based on the experimental results at a certain frequency and under the different temperatures.
3.2.1. Time-temperature superposition (TTS) and WLF formula
For the high polymer material with the density of , the stiffness of and at the frequency of and the Kelvin temperature of can be converted as the stiffness of and at the naturalized frequency of and the reference temperature of by the following Eq. (20)-(21).
In Eq. (20)-(21), is the conversion coefficient of temperatures, is the test Kelvin temperature (unit: K), is the reference temperature (unit: K); is the test frequency (unit: Hz), is the naturalized frequency (unit: Hz); is the density at the test temperature of (unit: kg/m3), is the density at the reference temperature of (unit: kg/m3).
In general, the influence of temperatures on the dynamic mechanical property of high polymer materials is far greater than the effect of frequencies, and these measurements to alter temperatures can be easily achieved in a broad temperature range. Therefore, the naturalized frequency of is much higher than the test frequency of . The conversion factor of can be calculated by WLF equation [22], see Eq. (22):
In Eq. (22), and are two constants, which has relation with the reference temperature of and the types of high polymer materials.
In order to obtain the temperature-dependent and frequency-dependent dynamic mechanical parameters of the test pads by application Time-Temperature Superposition (TTS) and WLF formula, the suggested procedure is as following.
(1) The centigrade scale (unit: °C) used in this test should be equivalent to the absolute scale (unit: K).
(2) The glassy transformation temperatures () of the test pads can be determined by their maximum temperature-dependent loss factors. In this test, the glassy transformation temperatures of WJ-7 rail pads are –40 °C, –45 °C and –45 °C, respectively. According to ISO4664-1, if the glassy transformation temperatures are regarded as the reference temperature, and are 17.44 and 51.6 K in WLF formula, respectively.
(3) If another temperature is regarded as the reference temperature, and at the corresponding reference temperature can be calculated by using Eq. (23)-(25):
(4) In terms of the corresponding constants () and () at the different reference temperatures, the conversion factor of can be calculated by WLF formula (Eq. (22)).
(5) The density of at the reference temperature of can be approximately obtained by using Eq. (26), in which the volume expansion coefficient of is 4.8×10-4/K:
3.2.2. Experimental parameters
In this test, the full-size rail pads of WJ-7 fasteners which was often used in China’ high-speed railway, the universal testing machine equipped with a temperature control box, a section of steel rail (60 kg/m), several emery cloths, a loading steel plate and two supporting steel plates (Fig. 5).
In view of China’s high-speed vehicle’s dynamic weight of 8×85 kN (increasing by 10 % than its actual static weight), the preload of two springs in a fastener (generally, about 20 kN) and the load-sharing scale of a fastener (generally, 0.4-0.6), the exciting dynamic loads on a rail pad should reciprocate between 20 kN and 70 kN. For safety’s sake, the periodic dynamic force-displacement curves of the test rail pads were measured at a certain frequency of 0.3 Hz and under the different temperature points of –60-+20 °C with an interval of 2.5 °C. The periodic dynamic force-displacement curves of WJ-7 rail pads at 0.3 Hz and under –30 and +20 °C are shown in Fig. 6.
Fig. 5a) Universal testing machine equipped with a temperature control box in which the dynamic mechanical parameters of the soft pads in b) WJ-7 fasteners are measured under –60-+20 °C


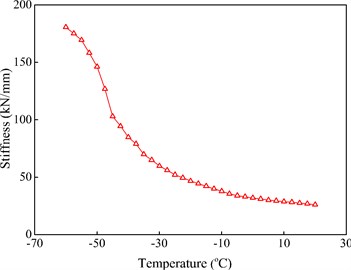
According to periodic dynamic force-displacement curves of linear viscoelastic materials, the stiffness of the soft pads in WJ-7 fasteners can be obtained at 0.3 Hz and under the temperatures of –60-+20 °C with an interval of 2.5 °C, as shown in Fig. 7.
Fig. 6The periodic dynamic force-displacement curves of WJ-7 rail pads at 0.3 Hz and under 20 °C
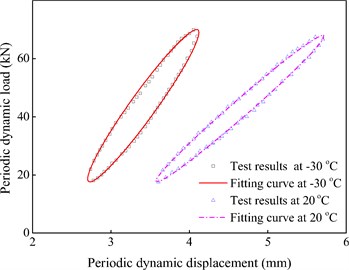
Fig. 7The stiffness of WJ-7 rail pad at 0.3 Hz and under the temperatures of –60-+20 °C
3.2.3. Prediction of the untested dynamic mechanical performances of rail pads
Since the dominant frequencies of the environment vibrations due to high-speed railway are low, only the stiffness of the soft pads in WJ-7 fasteners within 1000 Hz are predicted under the temperatures of –60-+20 °C.
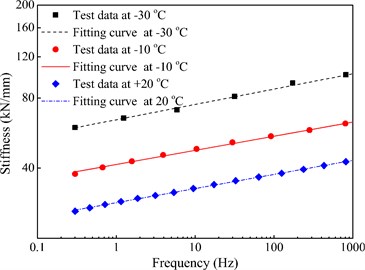
Fig. 8 shows the frequency-dependent stiffness of the test pads in WJ-7 fasteners within 1000 Hz and under –30, –10 and +20 °C. It is clear that the actual dynamic mechanical parameters of rail pads are not supposed to be the frequency-independent and temperature-independent constants. Overall, the stiffness of rail pads increase with the decrease of temperatures or the increase of frequencies.
It can be found that the stiffness of rail pad of different kinds of high polymer materials and the excitation frequency approximately form a linear relationship under the logarithmic coordinate system [23-25], as expressed in Eq. (27):
where is the low-frequency initial stiffness of the rail pad at the low excitation frequency (usually 3-5 Hz); is the slope of the linear relationship between the rail pad stiffness and excitation frequency under the logarithmic coordinate system, representing the frequency-dependent extent (or frequent-dependent degree) of the rail pad stiffness. It can be easily seen from Eq. (27) that the relationship between the stiffness of rail pad of different materials and the excitation frequency mainly depends on its low-frequency initial stiffness and its stiffness' frequency-dependent extent .
According to the experimental data, the linear slope for the changes in the stiffness of WJ-7 rail pad with the frequency under the logarithmic coordinate system is all 0.07 under –30, –10 and +20 °C; in addition, the initial stiffness of WJ-7 rail pad is 31.0, 45.2 and 70.8 kN/mm under an excitation of 3-5 Hz.
Fig. 8The frequency-dependent stiffness of WJ-7 rail pad within 100 Hz and under –30, –10 and +20 °C
3.3. The impact of the rail pad frequency-dependent stiffness on the random vibration response of the coupled vehicle-track system
The comparison of impact the rail pad frequency-dependent stiffness and constant stiffness on the random vibration response of the coupled vehicle-track system at the temperature of 20 °C was presented. The vertical random vibration acceleration of the vehicle body, bogie, wheelset and rail under these two calculation conditions are shown in Fig. 9-12.
Fig. 9 shows the PSD of the vertical random vibration acceleration of the vehicle body under the rail pad constant stiffness and frequency-dependent stiffness. It can be seen from Fig. 9 that the calculation results under the two calculation conditions basically overlap. This result suggests that the impact of the rail pad frequency-dependent stiffness on the vertical random vibration response of the vehicle body can be neglected.
Fig. 10 presents the PSD of the vertical random vibration acceleration of the bogie under the rail pad constant stiffness and frequency-dependent stiffness. It can be seen from Fig. 10 that the calculation results under the two calculation conditions have very little difference within 15 Hz. By reading the PSD peak value at 7.02 Hz, we can know that there is only a small gap of 2.0×10-6 m2/s4/ Hz between these two conditions, as shown in Fig. 10(a). However, as the frequency varies within 20-100 Hz, there is a huge difference between them, as shown in Fig. 10(b). For example, when the frequency varies within 20-45 Hz, given that the calculation condition of the frequency-dependent stiffness of rail pads has a small calculation value, namely, the calculation result under the rail pad frequency-dependent stiffness is 88.5 % of that under the rail pad constant stiffness at Point A in Fig. 10(b); yet, with the frequency range of 45-100 Hz, the calculation result under the constant stiffness condition is small, namely, the calculation result under the rail pad constant stiffness is only 56.1 % of that under the rail pad frequency-dependent stiffness at Point B in Fig. 10(b). Thus, it is not hard to find that the calculation result without considering the frequency-dependent stiffness of the rail pads will not only underestimate the vibration of the bogie within the frequency range of 45-100 Hz but also overestimate the vibration with the frequency range of 20-45 Hz. In other words, the rail pad characteristic of the frequency-dependent stiffness changes the distribution of the random vibration of the bogie in the frequency domain.
Fig. 9PSD of vertical random vibration acceleration of the vehicle body
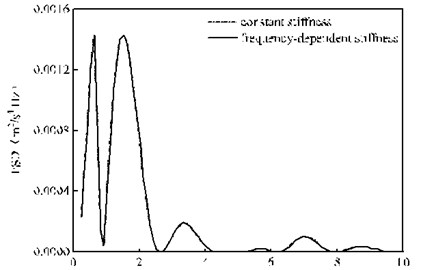
Fig. 10PSD of the vertical random vibration acceleration of the bogie
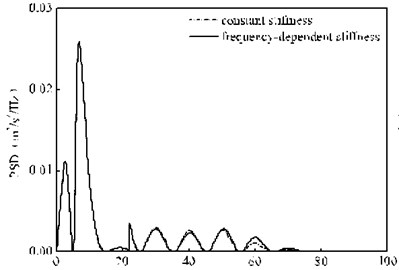
a) 0-100 Hz
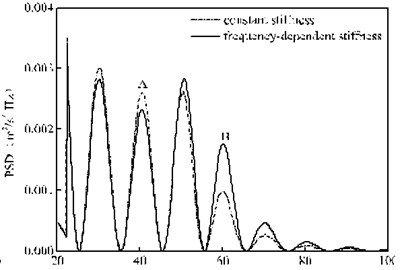
b) 20-100 Hz
Fig. 11 shows the PSD of the vertical random vibration acceleration of the wheelset under two different calculation conditions. It can be seen that, the frequency-domain random vibration acceleration of the wheelsets mainly concentrate within the range of 30-100 Hz. In addition, it can be seen from Fig. 11 that, compared with the calculation condition of rail pad constant stiffness, the frequency-dependent stiffness not only significantly increases the vertical random vibration acceleration of the wheelset within the frequency range of 50-200 Hz, but also enhances the 1st dominant frequency. Fig. 11 suggests that, when the rail pad stiffness is constant, the highest PSD peak of the vertical random vibration acceleration of the wheelset reaches 8.82 m2/s4/Hz and corresponds to the 1st dominant frequency of 47.9 Hz; when the rail pad stiffness is frequency-dependent, the highest PSD peak of the vertical random vibration acceleration of the wheelset rises to 13.5 m2/s4/Hz and its corresponding 1st dominant frequency also increases to 57.1 Hz. To sum up, the frequency-dependent stiffness of rail pad alters not only the frequency-domain amplitudes of the vibration but also its frequency-distribution at center frequencies higher than 30 Hz. The random vibration of the wheel is transferred to the high frequency in the frequency domain.
Fig. 12(a) shows that in the range of 0-100 Hz, the effect of frequency-dependent rigidity on the random vibration of the rail is basically the same as that of the wheelset, that is, the frequency-dependent stiffness of rail pads clearly decreases the random vibration of rail below 50 Hz, and significantly increases the random vibration of rail above 50 Hz. In the frequency range of 100-1000 Hz, the PSD peak fluctuation of the rail vibration acceleration power spectrum is very severe, which is caused by the periodic vibration of the rail due to the fixed wheelbase according to the existing research [26]. There is a peak at 840 Hz, which is mainly due to the self-vibration characteristics of the rails, on the overall trend of the rail acceleration PSD. Fig. 12(b) shows that every two adjacent peaks of the rail vibration acceleration PSD between the frequency interval is equal to (10 Hz), where is the vehicle speed, is a fixed wheelbase. In addition, the influence of frequency-dependent stiffness on the response of the rail vibration acceleration becomes very small in this frequency domain, and the difference between the two cases is only 1 %. The random vibration curve of the rail is the shape of the wave mainly due to two reasons which are due to the periodic vibration caused by the fixed wheelbase of the vehicle body and the free-vibration characteristic of the track structure itself.
Fig. 11PSD of the vertical random vibration acceleration of the 2nd wheelset
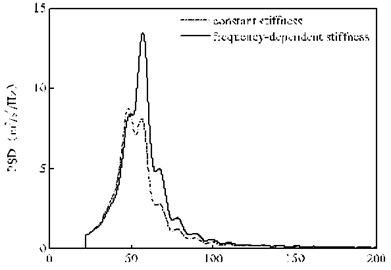
Fig. 12PSD of the acceleration of the rail the under the 2nd wheelset
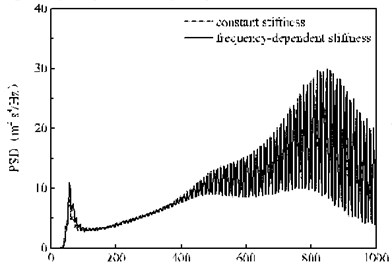
a) 0-1000 Hz
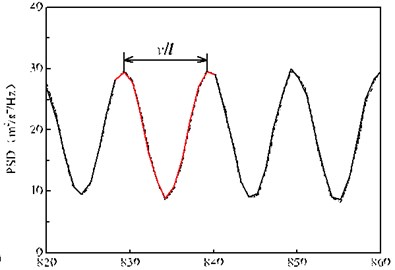
b) 820-860 Hz
3.4. The impact of the environment temperature on the random vibration response of the coupled vehicle-track system
The experimental results show that the stiffness of the fastener is not only affected by the excitation frequency, but also has a great relationship with the environment temperature. In this section, we will study the influence of the frequency-dependent and temperature-dependent stiffness of the rail pads on the random vibration of the vehicle-track coupled system. In this analysis, the frequency-dependent extent of the rail pads stiffness is taken as 0.07 and the environment temperature is considered as –30, –10 and 20 °C.
Fig. 13 shows the random response of the vehicle body under three temperature conditions. The calculated results are in good agreement with each other, indicating that the impact of the rail pads temperature-dependent stiffness on the response of the vehicle body is negligible.
Fig. 14 shows the random vibration acceleration response spectrum of the bogie at three temperatures. Fig. 14(a) can be seen that the calculation results of the three conditions in the 0-20 Hz range is basically the same, but the difference in the 20-100 Hz range is obvious. Fig. 14(b) shows that at the peak A position, the bogie acceleration response PSD peak at the three ambient temperatures (–30, –10 and 20 °C) is 4.51×10-3 m2/s4/Hz, 1.78×10-3 m2/s4/Hz and 4.60×10-4 m2/s4/Hz, respectively corresponding to the dominant frequency of 71.2 Hz, 70.0 Hz and 70.0 Hz. In summary, the temperature-dependent stiffness of the rail pads only affects the amplitude of the PSD in the frequency domain above 20 Hz, and the influence on the main frequency is relatively small. With the frequency of 63 Hz as the critical position, when the frequency is less than 63 Hz, the higher the temperature, the PSD peak of the bogie random vibration acceleration greater, but when the frequency is more than 63 Hz, the conclusion is just the opposite. It indicates that the law of the temperature-dependent stiffness of the rail pads on the random vibration of the bogie is different in different frequency bands.
Fig. 13PSD of vertical random vibration acceleration of the vehicle body
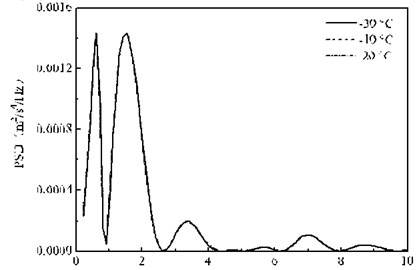
Fig. 14PSD of the vertical random vibration acceleration of the bogie
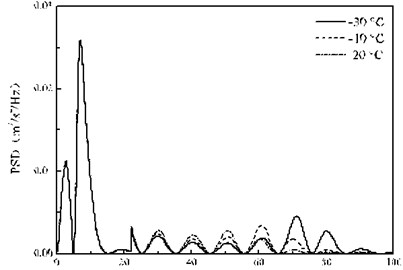
a) 0-100 Hz
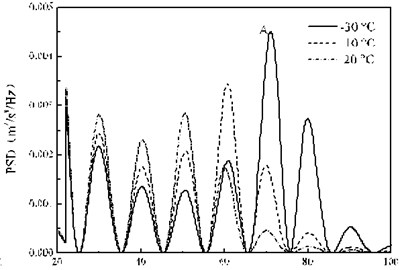
b) 20-100 Hz
Fig. 15 shows the results of the wheelset acceleration PSD under three ambient temperatures. It is not difficult to find that the temperature variation stiffness of the fastener has great influence on the wheel acceleration response, including the peak value and the corresponding dominant frequency. The PSD peak of the wheelset acceleration response is 63.4 m2/s4/Hz, 27.5 m2/s4/Hz and 13.1 m2/s4/Hz respectively, and the corresponding dominant frequencies are 73.4 Hz, 63.1 Hz and 50.3 Hz. The lower the temperature, the greater the peak value of the wheelset acceleration PSD and the higher the corresponding dominant frequency, and this change was a nonlinear increase in the trend. This is because the rail pads stiffness decreases gradually with the temperature, making the resonance frequency of the wheel-rail coupled system increases, so that the energy of wheel random vibration transfer to the high-frequency domain. As the temperature increases linearly, the increasing trend of the peak value of the random vibration acceleration PSD of the wheel is nonlinear.
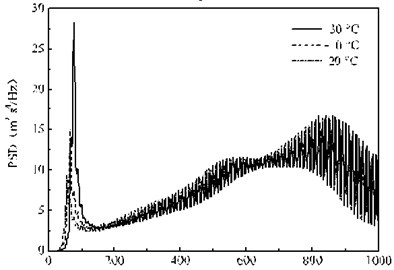
Fig. 16 shows the random vibration PSD of the rail under three temperatures. The influence of the rail pads temperature-dependent stiffness on the rail acceleration is the same in the range of 0-200 Hz, and the effect of temperature on the rail acceleration response is gradually reduced in 200-600 Hz. The difference between the three temperature conditions is stable above 600 Hz, and the difference is less than 5 %. It is shown that the rail pads temperature-dependent stiffness only affects the rail acceleration within 200 Hz, but less on the high frequency vibration above 200 Hz. Because the fastener is in direct contact with the rail, the stiffness of the fastener pad has a certain influence on the whole frequency domain of the rail, and the influence law is complicated and nonlinear.
Fig. 15PSD of the 2nd wheelset acceleration
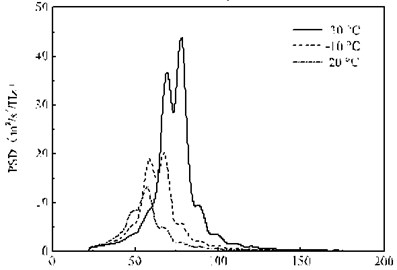
Fig. 16PSD of the acceleration of the rail under the 2nd wheelset
With the comparison of Fig. 11 and Fig. 15, considering the range of environment temperature and the frequency-dependent extent of the rail pads of WJ-7 fastener, the PSD peak of the vertical random vibration acceleration of the wheelsets gets the maximal increase of 3.3 times at least, and its 1st dominant frequency has the biggest increment of 20.6 Hz or more. Therefore, in order to accurately analyze the random vibration responses of the vehicle-track coupled system, experiments must be conducted to obtain the accurate kinetic parameters of the polymer materials like rail pads.
4. Conclusions
The symplectic method and random vibration pseudo-excitation method of infinitely periodic substructure are adopted to establish an efficient symplectic model of vertical random vibration of the vehicle-track coupled system for exploration of the impact of the rail pad frequency-dependent and temperature-dependent stiffness on the vertical random variation response of the vehicle body, bogie, wheelsets and rail. The conclusions and suggestions are as follows:
1) According to Time-Temperature Superposition (TTS) and WLF formula, the temperature-dependent and frequency-dependent dynamic mechanical parameters of rail pads can be predicted based on the experimental results at a certain frequency and under the different temperatures. The frequency-dependent stiffness of the test rail pads in WJ-7 fasteners within 1000 Hz is predicted under the temperatures of –30, –10 and +20 °C, and the predicted results show that the rail pads stiffness increase with the decrease of temperatures or the increase of frequencies.
2) The impact of rail pad frequency-dependent stiffness on the vertical random vibration of the vehicle body is negligible; yet, it will change the vertical random vibration amplitude of the bogie with the frequency range of 20-100 Hz and significantly improve the PSD peak of the vertical random vibration acceleration of the wheelsets and rail and its corresponding 1st dominant frequency, thereby causing the frequency domain redistribution of the vertical random vibration of the bogie, wheelsets and fundamental structure under wheels.
3) The random vibration of the vehicle-track coupled system under different temperature is studied considering the rail pads stiffness variation with the excitation frequency. The influence of the rail pads temperature-dependent stiffness on the response of the vehicle body is negligible, but the influence on the acceleration of the bogie, wheelset and rail is significant in the frequency range of 20-100 Hz. For the response of the wheelsets and rail, the lower the temperature, the greater the peak value of the wheelset acceleration PSD and the higher the corresponding dominant frequency, and this change presented a nonlinear increase on the trend.
4) Within the range of environment temperature and the frequency-dependent extent of rail pads in the railway, the PSD peak of the vertical random vibration acceleration of the wheelsets and rail gets the largest increase of 3.3 times at least, and the maximum increment for their 1st dominant frequency also reaches up to 20.6 Hz or more. Therefore, in order to accurately predict the random vibration responses of the vehicle-track coupled system, experiments must be conducted to obtain the accurate kinetic parameters of the polymer materials like rail pads.
References
-
Zhai W. M., Sun X. A detailed model for investigating vertical interaction between railway vehicle and track. Vehicle System Dynamics, Vol. 23, Issue 23, 1994, p. 603-615.
-
Dumitriu D., Baldovin D., Sireteanu T. Numerical simulation of the vertical interaction between railway vehicle and track. Proceedings of the Annual Symposium of the Institute of Solid Mechanics with International Participation, Bucharest, 2004
-
Popp K., Kaiser I., Kruse H. System dynamics of railway vehicles and track. Archive of Applied Mechanics, Vol. 72, Issue 11, 2003, p. 949-961.
-
Lund J. W. Stability and damped critical speeds of a flexible rotor in fluid-film bearings. ASME Journal of Engineering for Industry, Vol. 96, Issue 2, 1974, p. 509-517.
-
Leung A. Y. T. An accurate method of dynamic substructuring with simplified computation. International Journal for Numerical Methods in Engineering, Vol. 14, Issue 8, 1979, p. 1241-1256.
-
Cai G. Q., Lin Y. K. Wave propagation and scattering in structural networks. Journal of Engineering Mechanics, Vol. 117, Issue 7, 1991, p. 1555-1574.
-
Mencik J. M. New advances in the forced response computation of periodic structures using the wave finite element (WFE) method. Computational Mechanics, Vol. 54, Issue 3, 2014, p. 789-801.
-
Mead D. J. Vibration response and wave propagation in periodic structures. Journal of Engineering for Industry, Vol. 93, Issue 3, 1971, p. 783-792.
-
Zhong W. X., Williams F. W. Wave problems for repetitive structures and symplectic mathematics. ARCHIVE Proceedings of the Institution of Mechanical Engineers, Part C, Journal of Mechanical Engineering Science, Vol. 206, Issue 63, 1992, p. 371-379.
-
Zhou M., Zhong W. X., Williams F. W. Wave propagation in substructural chain-type structures excited by harmonic forces. International Journal of Mechanical Sciences, Vol. 35, Issue 11, 1993, p. 953-964.
-
Lin J. H., Zhang W. X., Li J. Structural responses to arbitrarily coherent stationary random excitations. Computers and Structures, Vol. 50, Issue 5, 1994, p. 629-633.
-
Lin J. H., Fan Y., Bennett P. N., Williams F. W. Propagation of stationary random waves along substructural chains. Journal of Sound and Vibration, Vol. 180, 1995, p. 757-767.
-
Lu F., Kennedy D., William F. W., Lin J. H. Symplectic analysis of vertical random vibration for coupled vehicle-track systems. Journal of Sound and Vibration, Vol. 317, 2008, p. 236-249.
-
Jones D. I. G. Handbook of Viscoelastic Vibration Damping. John Wiley and Sons, New York, 2001.
-
Carrascal I. A., Casado J. A., Polanco J. A., et al. Dynamic behavior of railway fastening setting pads. Engineering Failure Analysis, Vol. 14, 2007, p. 364-373.
-
Luo Y., Liu Y., Yin H. P. Numerical investigation of nonlinear of properties of a rubber absorber in rail fastening systems. International Journal of Mechanical Sciences, Vol. 69, 2013, p. 107-113.
-
Squicciarini G., Thompson D. J., Toward M. G., et al. The effect of temperature on railway rolling noise. Proceedings of IMechE, Part F: Journal of Rail Rapid Transit, 2014
-
Smutny J. Measurement and analysis of dynamic and acoustic parameters of rail fastening. NDT&E International, Vol. 37, 2004, p. 119-129.
-
Lin T. R., Farag N. H., Pan J. Evaluation of frequency dependent rubber mount stiffness and damping by impact test. Applied Acoustics, Vol. 66, 2005, p. 829-844.
-
Oregui M., Man A. D., Woldekidan M. F., et al. Obtaining railpad properties via dynamic mechanical analysis. Journal of Sound and Vibration, Vol. 363, 2016, p. 460-472.
-
Remington P. J. Wheel/rail rolling noise, I: Theoretical analysis. The Journal of the Acoustical Society of America, Vol. 81, Issue 6, 1987, p. 1805-1823.
-
Dooliffle A. K. Studies in Newtonian flow II – The dependence of the viscosity of liquids on free space. Journal of Applied Physics, Vol. 22, 1955, p. 1471-1475.
-
Thompson D. J., Verheij J. W. The dynamic behaviour of rail fasteners at high frequencies. Applied Acoustics, Vol. 52, Issue 1, 1997, p. 1-17.
-
Fenander A. Frequency dependent stiffness and damping of railpads. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, Vol. 211, 1997, p. 51-62.
-
Maes J., Sol H., Guillaume P. Measurements of the dynamic railpad properties. Journal of Sound and Vibration, Vol. 293, 2006, p. 557-565.
-
Ju S. H., Lin H. T., Huang J. Y. Dominant frequencies of train-induced vibrations. Journal of Sound and Vibration, Vol. 319, 2009, p. 247-259.
About this article
This research was supported by National Youth Natural Science Foundation of China (Grant No. 51608460), National Natural Science Foundation of China (Grant No. 51578468), National Outstanding Youth Science Foundation of China (Grant No. 51425804), Joint Funds from both Chinese High-speed Railway Company and the National Natural Science Foundation of China (Grant U1434201).
