Abstract
An efficient identification method of the dynamic properties of viscoelastic damping materials using an optimization technique is proposed. A Zener fractional derivative model is used to describe the frequency-dependent dynamic characteristics of materials. In this study, the viscoelastic material is used in a Passive Constrained Layer Damping (PCLD) configuration in order to increase the shear deformation in the material. Mean Square Velocities (MSVs) of a clamped-free beam covered with a PCLD patch are measured in an environmental chamber at different frequencies and used as reference MSVs. The excitation force is performed thinks to a low mass magnet fixed on the beam and placed inside a coil subjected to an electrical current. Numerical MSVs are calculated using an equivalent single layer plate model with warping functions chosen to ensure continuity of transverse shear stresses and displacements layer's interfaces.
1. Introduction
Over the past few years, passive damping treatments have been used increasingly in industrial applications, especially in the automotive and aeronautic industries. Viscoelastic constrained layer damping patches are added to structures to increase the vibrational energy dissipation. Modelling the behavior of such devices can't be done with classical models due to the high Young's modulus ratio between materials. In addition, the viscoelastic materials properties depend on environmental factors. This often translates into a frequency and temperature dependence. Hence, understanding how viscoelastic materials behave within structures is crucial for optimal design and successful applications.
Generally, the viscoelastic properties of materials can be measured using a rapid visco analyzer. However, these experimental measurements may not be easy to perform and can imply high costs. In addition, these tests are generally performed on small samples whose dimensions are not representative of the dimensions of the treated structures. Thus, identifying viscoelastic materials properties directly from the structure using classical vibrational testing devices becomes a faster and cheaper solution. These methods may also be used for in situ measurements to directly perform control or diagnosis of treated structures.
For these reasons several authors [1-4] have developed identification methods in order to measure viscoelastic material properties. As suggested by [5], identification methods can be classified in two groups: classical methods that work with rigorous mathematical principles, and non-classical methods based on heuristics concepts. For this last category, efficiency often needs a high computational work. However, these methods overcome some drawback of classical methods like local extrema trap. They are also easier to implement since they do not require a complete insight of the problem: the same strategy could be used for a large variety of problems.
For vibration problems, several methods have been developed to identify material properties, i.e. comparing experimental results with numerical simulations using different strategies and criteria [6]. For example, Elkhaldi [4] applied a gradient method to predict the viscoelastic behavior of damped sandwich structures minimizing an objective function that contains the difference between simulated and observed structural damping properties. Other authors like Kim [3] searched the parameters of the fractional-derivative model to describe the dynamic behavior of viscoelastic materials. They used a finite element model for simulations and simply structure covered with a viscoelastic material for their experimentation. Some works done with such algorithms have been carried out to identify material properties for vibration problems. Hawng [7] and Cunha [8] combine vibration experimental results and numerical solutions, using a Genetic Algorithm to minimize the differences between natural frequencies in undamped systems.
As a novel heuristic computational method, Bang-Big Bang-Crunch (BB-BC) [9] is a heuristic computational algorithm for solving complex optimization problems. It is a global optimization method which take inspiration from the theories of the evolution of the universe, namely, the Big Bang-Big Crunch theory. The BB-BC algorithm uses random points in the Big Bang phase and shrinks those points to a single center of mass during the Big Crunch phase. After several iterations, the size of the search space solution is reduced, causing the convergence of the algorithm to a single solution.
This work presents an identification method of the parameters of a viscoelastic material used in a passive constrained layer damping configuration. The frequency dependence of the Young's modulus and loss factor of the viscoelastic material are described by a fractional derivative Zener model. The viscoelastic material to be characterized is inserted into patches bonded to a base structure consisting of an aluminum beam. An identification procedure of the parameters of the fractional derivative Zener model is proposed. The proposed method minimizes the difference between the simulated and measured Frequency Response Functions (FRFs) of a damped beam using a BB-BC numerical algorithm.
2. Viscoelastic properties of materials
For a viscoelastic material, the rheological model linking stress and strain is written in a general form:
where is the time fractional derivative of order (). is the relaxation time and is the Young’s modulus. The rheological element associated to this equation has intermediate characteristics between those of the spring and damper or dashpot, it is therefore called a spring-pot. Thus, when , the behavior of the element depends only on the characteristics of parameters of the present time, while for , the behaviour depends on the neighbouring moments of the present time. For , the -order fractional derivative depends on the whole history of the function in the past and it is said that in this case there is a memory effect because of the parameter .
There are several models to describe the behavior of a viscoelastic material in the structural dynamic domain. The most widely known model which uses a reduced number of material parameters for characterization is the Fractional Derivative Zener model described by Eq. (2) and shown in Fig. 1.
Fig. 1Representation of the fractional derivative Zener model
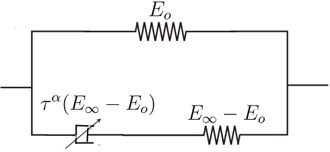
In the case of a steady state harmonic excitation, the complex modulus is derived from Eq. (2) where the fractional derivative operator is replaced by a multiplication by . is the imaginary unit .
represents the limit value of Young’s modulus at low frequencies while represents its limit for high frequencies.
It is possible to write Eq. (3) in the form of Eq. (6):
where . represents the material loss factor. The real part of this complex modulus, which gives the elastic behavior of the material is also called storage modulus. The imaginary part or loss modulus, represents the viscous or damping behaviour of the material.
This fractional-derivative model can sufficiently represent the real behavior of viscoelastic materials over a wide frequency range [7]. To identify the parameters of the viscoelastic material, the error between the numerical values and the experimental data are minimized using the BB-BC technique.
3. BB-BC algorithm
The initialization of the optimization process based on the BB-BC algorithm is performed by choosing a set of solutions obtained randomly ( ); being the population size. This set represents the initial population generation. In this stage, solutions are spread over the entire search space in a uniform manner. This first stage, called Bing Bang, is followed by a step of concentrating of all solutions to get a single solution . In this stage called Big-Crunch phase, the algorithm takes each candidate solution in the population and its associated fitness function value to compute the “center of mass”
The new solutions for the next iteration are normally distributed around the “center of mass” :
where is the standard deviation of a standard normal distribution.
is a random number from a standard normal distribution; a is a parameter to limit the size of the search space; and are the upper and lower limits defining the space search. is a parameter to control the size decay of the search space. Since the standard normal distribution can give numbers greater than unity, it is necessary to limit the solution to the search space delimiter by and . The BB-BC algorithm increments the iteration number until the stopping criterion is satisfied. It should be noted that the size of the population must be large enough to ensure convergence toward the optimum point.
To improve the efficiency of the algorithm, the contributions of the best solutions are added to the center of mass as indicated in the following equation:
where is the best solution obtained at the iteration. is a weighting coefficient.
4. Application
In this study, the identification process is performed on an aluminum beam covered with PCLD patches (damped beam (B)) and a bare beam (undamped beam (A)). The two beams have the same size (13 mm×172 mm×0.77 mm). The viscoelastic material is a VHB4905 manufactured by 3M company. To obtain the experimental responses, many FRFs with an environmental chamber were carried out.
4.1. Test set-up
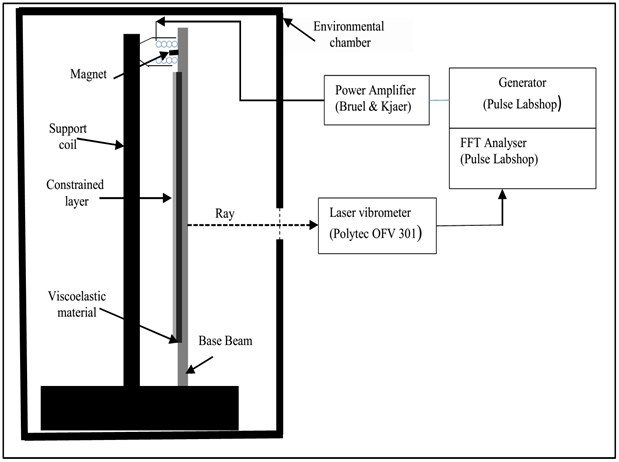
Fig. 2 shows a schematic diagram of the clamped beam structure and the test set-up. The test bench consists of a modified Obesrt test device. A Polytec Laser vibrometer and Pulse-Labshop software were used to acquire the FRFs signals. The excitation force is achieved using a low mass magnet glued to the test beam. The magnet is placed inside a coil. It is crossed by an electrical current of low intensity.
Fig. 2Schematic diagram of the test set-up
4.2. Results for undamped beam (A)
The Mean Square Velocity (MSV) integrated over the measuring frequency band is chosen as the objective function for the optimization process. For each proposed solution, the MSV is computed and compared to the experimental results. The two parameters to be identified are the Young's modulus and the loss factor of the aluminum. The search space is a set of 2-dimension vectors containing Young’s modulus and loss factor. The initial population is obtained by generating a set of 10 vectors in an interval whose limits are and ; being the standard parameters of aluminum.
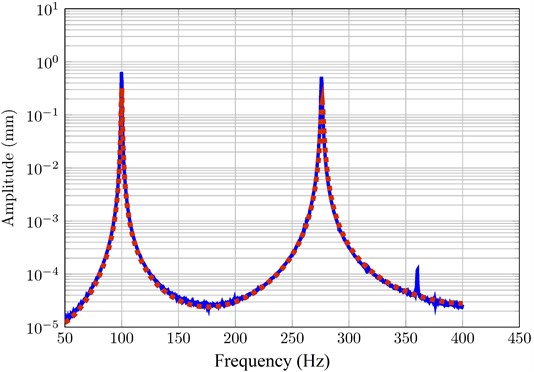
Fig. (3) shows the experimental and the calculated FRFs for the bare beam (A). One can see a good agreement between the two results. The estimated material properties of the bare beam are: 7.1e10 and 0.27 %. The material properties of the aluminum used are listed in Table 1.
Fig. 3Experimental and the calculated FRFs for the bare beam (A)
4.3. Results for damped beam (B)
Aluminum characteristics identified in the previous step, density of the viscoelastic material as well as the dimension of the tested sample are listed in Table 1.
Table 1Properties of materials
Base beam | Viscoelastic layer | Constrained layer | |
(Aluminum) | (BHV-3M) | (Aluminum) | |
Length(mm) | 172 | 172 | 172 |
Width(mm) | 13 | 13 | 13 |
Thickness (mm) | 0.77 | 0.5 | 0.2 |
Densitu (kg/m3) | 2700 | 1000 | 2700 |
Young Modulus(Pa) | 7.1×1010 | – | 7.1×1010 |
Poisson ratio | 0.3 | 0.45 | 0.3 |
Loss factor | 0.27 % | – | 0.27 % |
Population size was set at 15. The parameters to be identified in this step are four coefficients used to define the complex young modulus in Eq. (3). The search space, in this case, is a set of 4-dimension vectors. The initial population is generated randomly around the first solution . The values of the original solution and the limits of the search space are listed in Table 2.
Table 2Limits of the search space
Standard | Minimum | Maximum | |
4.5×105 | 1.5×105 | 13.2×105 | |
8.8×107 | 2.93×107 | 26.4×107 | |
1.7×10-5 | 0.57×10-5 | 5.1×10-5 | |
0.63 | 0.21 | 1.89 |
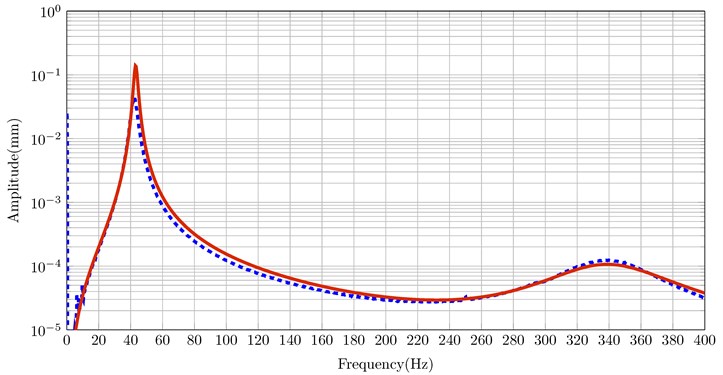
Fig. 4Comparison of the experimental and numerical responses of the plate with viscoelastic material
5. Conclusion
A method to identify the frequency-dependent properties of a viscoelastic material used in Passive Constrained Layer Damping (PCLD) patches for reducing vibration levels is proposed. The method is based on the convergence of the numerical mean square velocity to the experimental one using a BB-BC algorithm. This method does not require significant equipment such as a visco analyzer but simply uses traditional vibration measurement equipment. Convergence to the reference results was achieved despite the very important ratio between the Young’s modulus of aluminum and that of the viscoelastic material.
References
-
Pagnacco E., Moreau A., Lemosse D. Inverse strategies for the identification of elastic and viscoelastic material parameters using full-field measurements. Materials Science and Engineering: A, Vols. 452-453, 2007, p. 737-745.
-
Hwang Shun-Fa, Chang Chao-Shui Determination of elastic constants of materials by vibration testing. Composite Structures, Vol. 49, Issue 2, 2000, p. 183-190.
-
Kim Sun-Yong, Lee Doo-Ho Identification of fractional-derivative-model parameters of viscoelastic materials from measured FRFs. Journal of Sound and Vibration, Vol. 324, Issues 3-5, 2009, p. 570-586.
-
Elkhaldi Imen, Charpentier Isabelle, Daya El Mostafa A gradient method for viscoelastic behavior identification of damped sandwich structures. Comptes Rendus Mecanique, Vol. 340, Issue 8, 2012, p. 619-623.
-
Perry M. J., Koh C. G., Choo Y. S. Modified genetic algorithm strategy for structural identification. Computers and Structures, Vol. 84, Issues 8-9, 2006, p. 529-540.
-
Zhang Z., Koh C. G., Duan W. H. Uniformly sampled genetic algorithm with gradient search for structural identification. Part I: global search. Computers and Structures, Vol. 88, Issues 15-16, 2010, p. 949-962.
-
Hwang Shun-Fa, Chihwu Jen, He Rong-Song Identification of effective elastic constants of composite plates based on a hybrid genetic algorithm. Composite Structures, Vol. 90, Issue 2, 2009, p. 217-224.
-
Cunha Jesiel, Cogan Scott, Berthod Christophe Application of genetic algorithms for the identification of elastic constants of composite materials from dynamic tests. International Journal for Numerical Methods in Engineering, Vol. 45, Issue 7, 1999, p. 891-900.
-
Erol O. K., Eksin I. A new optimization method: big bang-big crunch. Advances in Engineering Software, Vol. 37, Issue 2, 2006, p. 106-111.
