Abstract
NAH method in non-free sound field reconstruction of the sound source will lead to considerable error. This paper proposes a method to reconstruct the sound source in a closed space. In the closed space, the total sound pressure is the sum of the source radiation pressure and the reflected sound pressure from medium interface. Reflections from medium interface is a convolution noise, rather than additive noise. In order to reconstruct a sound source in the closed space, in this paper we first adopt the complex cepstrum method to separate and radiation pressure and the reflected sound pressure, then filter them to reduction of reflected sound pressure, and then reconstruct the sound source. The simulation results show the correctness and effectiveness of the method.
1. Introduction
In the early 1980s, american scholar E. G Williams put forward the concept [1, 2]. NAH considering the effect of evanescent waves, breaking the Rayleigh criterion limiting the resolution of reconstruction in recent years has been widely used. NAH is different from of the far field acoustic holography. In the holographic surface near the sound source surface, the measurement data is recorded. The sound pressure is then reconstruct three-dimensional sound field, sound intensity, and particle velocity by the Fourier technology. Since the limit of the two
-dimensional Fourier transform itself, planar NAH required the measured surface should be conformal of the sound source [3], in order to make NAH can be applied to any surface shape of the sound source, the boundary element method [4] have been proposed. Xinzhao Chen propose the distributed source boundary point method [5], further simplifying the tedious calculations boundary element method for the coefficient matrix. In order to improve the accuracy of the reconstruction effectively, many scholars in-depth study of the data interpolation and extrapolation methods [6-10].
Planar NAH basing on spatial sound field transformation requires sound field to be free-field measurements, which severely limits the planar NAH applications. Dual holographic [11] located on different sides of the holographic interference source separation plane NAH further expand its application, but the application plane NAH reconstruction of the sound source in an enclosed space will still produce large errors. In this paper, the complex cepstrum preprocess the measured data before reconstruction, to eliminate or weaken the effects of reflected sound.
2. The theory of the planar acoustic holography
The acoustic wave propagation satisfies the equation [12] in the three-dimensional ideal fluid medium:
The solutions of the above three equations is:
Fourier transform on both sides, we can obtain:
where is the frequency domain pressure; is the wave number; is the circular frequency; is the speed of sound.
The formula is Helmhotz equation, the equation always hold to steady sound. The solution of Eq. (3) can be expressed as the Kirchhoff integral:
where is a closed surface, is the distance from the point to the origin from the field, is the distance from the sound source surface to the point in the sound field, is the complex sound pressure, is Green’s function.
In an infinite radius hemispherical surface of the sound field, Eq. (4) can be expressed as:
Semi-free sound field infinity meet sommerfeld radiation conditions, Eq. (5) in the second integral is zero, so Eq. (5) simplifies to:
In actual sound field, the sound pressure distribution satisfies Dirichlet conditions, the Green’s function is:
Meet the conditions for the Green’s function expression:
where is the distance from the sound source surface, Eq. (6) simplifies to:
In the Cartesian coordinate system, Eq. (9) can be express as:
According to the convolution theorem there is:
where:
From Eq. (12) can be introduced:
Calculated in accordance with Eq. (13) can reconstruct surface sound pressure angular spectrum, then the two-dimensional inverse Fourier transform to seek sound pressure.
Sound field model in the enclosed space and complex cepstrum technology
Due to the presence of free-field conditions strictly, sound field approximation we encounter are generally enclosed spaces non-free field. In an enclosed space, sound waves are medium interface reflection, radiation, the presence of reflected waves in the sound field. In the closed space of the sound in a schematic view [13] as shown in Fig. 1.
Fig. 1Enclosed space sound field schematic
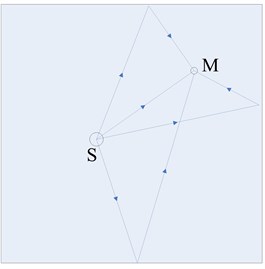
As can be seen from Fig. 1:
where is the noise, is the Reflection coefficient, is the signal of reflection, is the signal of sound source, is the total signal. Ignore the noise, then Eq. (14) can express:
Convolution represented by the formula:
where is impulse response of the room. From the Eq. (17), acoustic reflection can be seen as a form of noise Convolution noise. While taking the Eq. (17) on both sides do Fourier transform and logarithmic:
Both sides of the equation called cepstral, design a passband filter make the disappear, and make Inverse Fourier transform of , then we can obtain :
Error is defined as:
3. Numerical simulation
In order to verify that difference of the sound signal before and after data processing, respectively, two and four-point source source reconstruction simulation have been done. Of the parameters of the simulation is the same, the enclosed space length, width and height, respectively, 1 m, 1 m, 1 m. Analysis of the frequency are 800 Hz, surface vibration velocity of the ball is 0.25 m/s, holographic measurement distance is 0.1 m, reconstructed surface distance is 0.05 m, holographic surface is 64×64 square planar array, planar array of edge length is 0.8 m. The close space impulse response is shown in Fig. 2. The characteristics of passband filter is shown in Fig. 3. Two-point and four-point source source simulation results shown in Fig. 4 to Fig. 9.
Fig. 2The close space impulse response
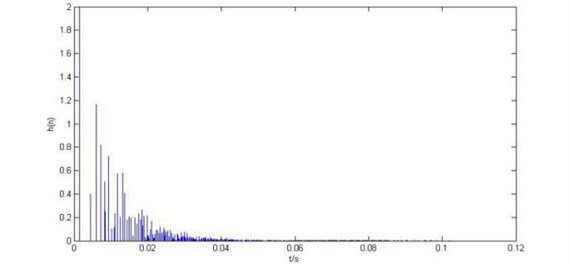
Fig. 3Bandpass filter amplitude-frequency characteristics
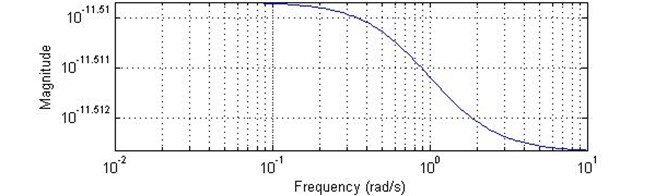
Fig. 4Theoretical sound pressure contours of two sound sources
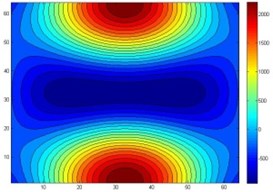
Fig. 5The reconstruction of two point sources acoustic pressure contours after data processing
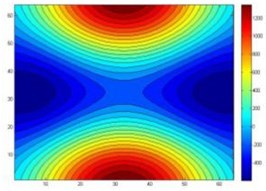
Fig. 6The reconstruction of two point sources acoustic pressure contours before data processing
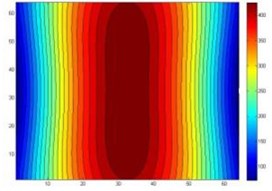
Fig. 7Theoretical sound pressure contours of four sound sources
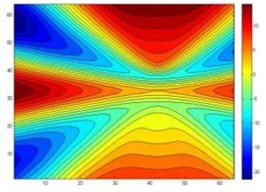
Fig. 8The reconstruction of four point sources acoustic pressure contours after data processing
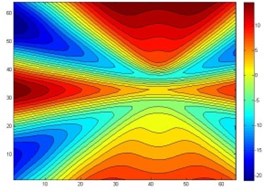
Fig. 9The reconstruction of four point sources acoustic pressure contours before data processing
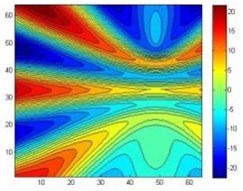
As can be seen from the simulation graph, the data of the two-point sources and four-point sources after the data processing could reconstruct the sound source precisely, there will be greater reconstruction error before data processing. For two sources, the sound source overlap portion is more, and cannot distinguish between two sources. For a four-point source, the sound pressure cloud also has a relatively large distortion. Error is shown in Fig. 10.
Fig. 10Error analysis figure
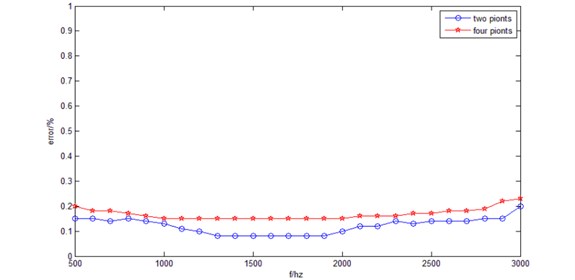
From Fig. 10, in the low frequency the error can be controlled within 20 %, the error of two sources is less than the error of four-point sources. In 1300 Hz to 1900 Hz band, two sources of error control in about 8 %, but with increased frequency, the error increases. This is caused by the complex cepstrum algorithm itself restricted, optimizing the parameters or combining with other reverberation algorithms the error can be controlled within a smaller range.
4. Conclusions
This paper proposes a method about reconstruction of the sound source in closed space with NAH. After receiving the flat plane array sound pressure data by the method of complex cepstrum data processing, data processed planar NAH sound source reconstruction. Simulation results show that the sound pressure level is very similar to the theoretical value of the post processed reconstruction of the sound source. In low frequencies, error analysis shows that the method of processing data for complex cepstrum method based on 1300 Hz to 1900 Hz frequency error control is good. The reason of the increasing of the error is that the parameters of the complex cepstrum algorithm cannot adjust adaptive the frequency increases, optimizing the parameters or combining with other reverberation algorithms could control the error within a smaller range.
References
-
Maynard J. D., Williams E. G., Lee Y. Nearfield acoustic holography I: Theory of generalized holography and the development of NAH. Acoustical Society of America, Vol. 78, Issue 4, 1985, p. 1395-1413.
-
Veronesi W. A., Maynard J. D. Nearfield acoustic holography (NAH) II: Holographic reconstruction algorithms and computer implementation. Acoustical Society of America, Vol. 81, Issue 5, 1987, p. 1307-1322.
-
Wan Haibo Study on the Reconstructing of the Underwater Radiated Sound Field from a Voyaging Submarine by Acoustic Holography Method. Naval University of Engineering, Wuhan, 2015.
-
Veronesi W. A., Maynard J. D. Digital holography reconstruction of sources with arbitrarily shaped surface. Acoustical Society of America, Vol. 85, Issue 2, 1989, p. 588-598.
-
Bi Chuanxing, Chen Jian, Zhou Guanglin, Chen Xinzhao Application of distributed source boundary point method in the sound field of holographic reconstruction and prediction. The Journal of Mechanical Engineering, Vol. 39, Issue 8, 2003, p. 81-85.
-
Zhang Dejun Vibrating body and the radiation field imaging using NAH. The Journal of Progress in Physics, Vol. 16, Issues 3-4, 1996, p. 613-623.
-
He Zuoyong Acoustic inverse problem – field acoustic holography technology and transform the source characteristics of discrimination. The Journal of Progress in Physics, Vol. 16, Issues 3-4, 1996, p. 600-612.
-
Yang Diange, Zheng Sifa Study on acoustic holography method for sound source identification. Journal of Acoustics, Vol. 26, Issue 2, 2001, p. 156-160.
-
Zheng Kai, Zheng Sifa, Yang Diange, et al. Acoustic holography spatial frequency domain analysis of the noise field reconstruction algorithm. The Journal of Tsinghua University, Vol. 42, Issue 2, 2002, p. 247-250.
-
Cheng Dezheng, Zhang Dejun Study on Chimes vibration characteristics using acoustic holography. Journal of Acoustics, Vol. 25, Issue 1, 2000, p. 87-92.
-
Yu Fei, et al. Double holographic sound field separation technique and its application to acoustic holography. Journal of Acoustics, Vol. 28, Issue 5, 2003, p. 385-389.
-
Chen Xinzhao, Bi Chuanxing NAH Technology and Its Application. Science Press, Beijing, 2013.
-
Su Xianli, He Peiyu The Study of Speech to Reverberation. Sichuan University, Chengdu, 2006.
