Abstract
This paper presents an investigation of quality evaluation of human upper extremity motions by introducing a new methodology. The VICON motion capturing system was applied to evaluate the kinematics of the upper extremity. The created 3D 5 DOF dynamical model in MATLAB allowed calculating additional movement’s quantitative parameters: the work done and power used during the appropriate motion. Finally, least squares method was applied to define torques by using a 3rd degrees polynomial approximation of mean torque values in the angle domain. The calculated parameters of 23 healthy participants’ motions as well as the investigated method could be used in the future in rehabilitation field to evaluate the quality of upper extremity motion of patients. The Pearson’s correlation coefficient between motion angle and angular velocity amplitudes is 0.49-0.82 and between work done and power of the movement is 0.61-0.99.
1. Introduction
The dysfunction of the upper extremity (UE) is one of the most common results after Central Nervous System (CNS) injuries [1, 2], surgical procedures or musculoskeletal impairments [3]. A dysfunction of the UE can significantly limit a person’s level of activity and participation in their social and physical environment [4]. The quantitative measures of UE movement quality are significant in the rehabilitation field for defining actual motion quality and recovery progress and it is very useful to apply an objective motion quality tool for rehabilitation program efficacy evaluation as well. That helps for physicians to accurately compare healthy and pathological movement conditions [5] in clinical setting.
Nowadays the most frequently used measurement tools in physicians practice for the UE assessment are subjective opinion and previously defined, standardized and validated clinical scales. It is easy to use and administer those scales but the main disadvantage of that tool is subjectivity; the result depends on the observer who scores the test and the experience of the observer. In case the same patient was evaluated by different observers, results of the same motion quality could be different. Subjective method couldn’t be easily applied for accurate rehabilitation program or motion recovery evaluation. Clinical scales have been classified into several categories such as strength, functional or activities of daily living (ADLs) tests [6]. The functional tests are classified into general clinical scales such as Jebsen-Taylor Hand function [7], Arm Research Assessment Test (ARAT) and Nine-Hole Peg Test and specific clinical scales applied to spinal cord injury (SCI) [6], stroke [8] or cerebral palsy (CP) [9]. The best-known ADL measures are Bartel Index [10] or Functional Independence Measure (FIM) [11] and specific Spinal Cord Independence Measure (SCIM) [12]. It is clear that only functional and clinical subjective scales are not enough for accurate motion quality measurements and objective methods in that case are required.
Idea to look for an objective UE motion evaluation tool is old enough. For more than 100 years, reaching movements have been studied in order to infer the visual and motor control or arm movements [13]. Woodworth performed some of the first quantitative experiments and found that the movements are composed of two phases: an approach phase followed by an adjustment phase [14]. Early in 1954, Fitt introduced the mathematical relationship among speed, accuracy, amplitude of movement, and target size for upper extremity tasks. That relationship, known as Fitt’s Law, provides a basis for objectively measuring neuromuscular performance capacities in a one-dimensional description way. The index of difficulty and the index of performance of motion are defined by Fitt’s Law [15].
In 1995, Kondraske extended Fitt’s Law from a translational movement to angular that is a common case involving one or more jointed body segments [16].
The kinematic model provides accurate and objective information about motion quality and the state of health. A. Reyes-Guzman et al. [17] declared that during the last fifteen years, many kinematic studies have been performed by using modern equipment during ADL in healthy people and who have suffered stroke.
Murphy et al. used motion capturing system Qualisys and investigated healthy participant’s motions during glass of water drinking [18] and repeated the same experiment with patients who have been suffered stroke [19]. Both experiments results were compared with results received from subjective scales. Kinematic data are a quantified measure of active and passive ranges of movement, the size of the workspace of the hand, the execution time, and the velocity of the movement. Kinematics also provides information about movement’s quality with respect to coordination, smoothness and other functional characteristics [19].
Kinematic analysis is one of the methods for objective testing and accurate evaluation of human UE motion. Kinematics describes movements of the body through space and time, including linear and angular displacements, velocities and accelerations, but without reference to the forces involved.
There are no studies, in our knowledge, which have analysed the UE motion kinematic and dynamic parameters with the same methodology as we have created for our recent experiment. The aim of the recent work is to present a three-dimensional dynamical model used to define the characteristic UE motion parameters for an objective UE movement’s quality evaluation and to introduce the methodology used for UE motion performance during the experiment. Tests were done with healthy participants in laboratory setting, where motion capturing system Vicon was used for UE motion numerical data collection. The goal of the research was to calculate kinematic and dynamic parameters that are peculiar for healthy persons at appropriate UE motion.
2. Experiment setup
The study group included 23 adult participants (10 males and 13 females). The average age was 29.2 years (range 19-63). The subjects’ height and body mass data were collected by self-report. UE segments’ masses were calculated by using anthropometric data from scientific literature [20]. The lengths of the arm segments were measured with a flexible measuring tape. The subjects’ average height was 1.71 m (range 1.55-1.85). All of the participants were right-handed. Inclusion criteria: nobody from participants in their opinion had any UE injuries that could influence kinematic results during the experiment.
The three-dimensional motion analysis was performed with a Vicon Motion Capture System (Vicon, USA). Experimental data were transferred to Windows-based data acquisition software (Vicon Nexus 1.7.1). Vicon system includes passive markers, sync box (or POE), 12 high resolution cameras with an infrared illumination, located on tripods and positioned around the testing area (approx. volume dimensions, m: Height×Width×Length ≡ 2.5×1.8×1.8). Measurements were performed at frequencies 60-100 Hz. Overall system accuracy was 63±5 µm and noise level of 15 µm, but during some cases because of dynamic calibration or arbitrary settings accuracy could be lower [21, 22].
For the UE experiment, a whole body Vicon system model was used and every time 39 passive retro-reflective spherical body markers positioned in special anatomical skeletal places [23] on the special participants’ suite surface. The markers positioned on the body reflect infrared light from camera flashes and only those markers are displayed on the whole-body model. The marker images produce , , coordinates values during measurements.
All of participants performed movements with their right and left arms. Subjects were standing in the marked experiment area and have been asked to perform hand motions according to the created experiment (Fig. 1) methodology. Each subject performed 4 sessions during the experiment. Two motions (elbow and shoulder) with the left and two with the right side. Prepared hand joints motions were chosen according to the usual biomechanical motions in human joints: flexion, extension, abduction and adduction. During the first session, the elbow joint flexion was investigated. The second session examined shoulder motions: flexion, extension adduction and abduction. Other side hand motions were the same. Each motion was repeated three times, i.e., during the shoulder joint motion testing, a participant made three flexion, then three extension, then three adduction and the same number of abduction. In case the appropriate joint motion was visually incorrect, it was repeated until correct motion was saved. During all introduced measurements, whole upper extremity segment’s positions were tracked.
Fig. 1a), b) Shoulder and c) elbow motions that participants needed to perform during the experiment: adduction, abduction, flexion, and extension
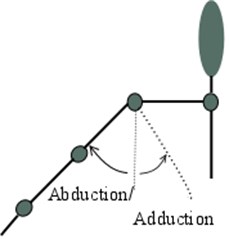
a)
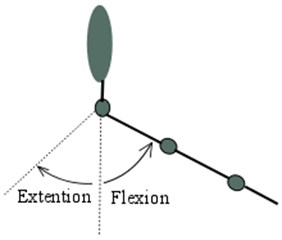
b)
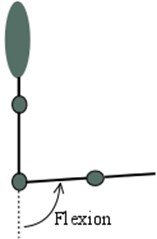
c)
Correct movement’s performances were demonstrated and the subjects were allowed to try them before doing the measurements. The warming up of muscles and joints was also done by participants before the experiment to avoid any injuries during the fast motions. When the subject was ready, he/she had to start the motion session as fast as possible. After all measurement sessions were completed, the participants changed the special suite and filled the blank where they declared gender, dominant site, age, height, body mass.
3. Method
After the experiment was completed, Vicon Nexus software was used to ensure if all markers were identified correctly through the data capture. Usually there were a few positions of the hand during the shoulder joint motions when markers were partly hidden or merged with other markers and could not be tracked automatically. But there was possible to define markers in each frame manually and to use an integrated software tools for the markers trajectory gaps filling. Only one motion measurements’ (from more than 136 trials) data file was unable to recover because of high segmentation and gaps. The dynamical processing in Vicon Nexus software allowed to convert coordinates into the angles of UE segments in local coordinate frame.
For further kinematic analysis the collected data was transferred to the MATLAB software. For every recording there were analysed angles of segments in time domain, calculated angular velocities and accelerations that were used in the created model. Correlation between outcomes was calculated by using Analysis Toolpak in Microsoft Excel.
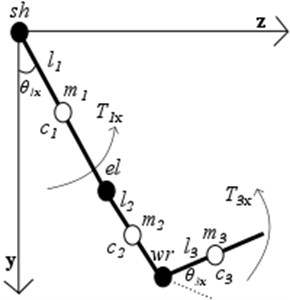
In order to investigate objectively the quality of UE motions and to collect characteristic dynamic parameters common for healthy participants, 5 degrees of freedom 3D simplified UE dynamical model consisting of three segments – the upper arm, the forearm and the hand was developed (Fig. 2). The upper arm, the forearm and the hand are able to rotate about rotating centres , , respectively (Fig. 2.). Segment’s masses , positions of centres of masses described according to anthropometrical data and depend individually on human body mass and height. Lengths were measured after the experiment, moments of inertia were selected on the basis from the scientific literature [20].
Fig. 2Simplified 3-D 3-segment dynamical UE model with shoulder (sh), elbow (el), wrist (wr) joints in sagittal (x-y) and frontal (z-y) planes: Ti – joint’s torques of each segment; θi – are generalized coordinates of each segments
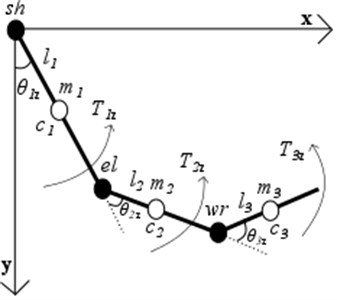
a)
b)
Eq. (1) represents the system of 5 second order differential equations describing motion of UE in sagittal and frontal planes which was formulated by using Lagrange energy method. The right-hand side of each equation in Eq. (1) is structured from derivative of total work function :
It is a common way to use inverse dynamics to calculate the torques , , , , at the joints caused by muscles that are needed to generate movements of segments from measured kinematic’s of an arm. System of equations represented as Eq. (1) was rewritten in into the Eq. (2) for expressing required joint torques . Where is inertia matrix, is vector of torques due to centripetal and Coriolis forces and – vector of joint torques due to gravity:
4. Results
The goal of the study was to look for objective kinematic and dynamic parameters that could show useful clinical information about healthy participant’s UE motions quality and can be comparable for further experiments with patients who are suffering from UE dysfunction.
To evaluate the performance of the shoulder and elbow joints with kinematic parameter’s, the mean of angle and mean of angular velocities (Fig. 3) amplitudes of all participants were calculated during the investigated motions.
Fig. 3Shoulder (Sh) and elbow (El) motions characteristic angle and angular velocities amplitudes and SD at appropriate motions: flexion (flex), extension (ext), adduction (add), abduction (abd)
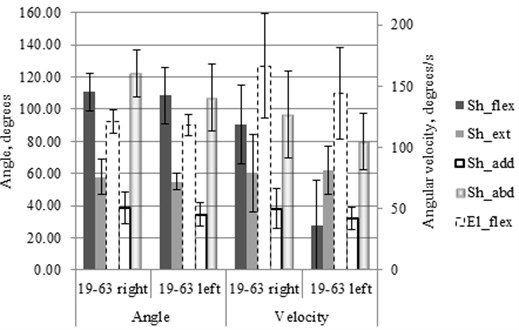
SD of angle amplitudes (Fig. 3) differs at the different motions. The lowest value was at the left shoulder extension (±5.2 deg.) and the biggest value was at the left shoulder abduction (±20.6 deg.).
SD of angular velocity amplitudes (Fig. 3) differs at the different motions as well as SD of amplitudes of the angles. The lowest value received at shoulder adduction (±7.2 deg/s) and the highest SD value was at the elbow flexion (±43.0 deg/s).
All participants were right-handed and it could be the reason why the right side motion’s kinematic parameters are better from 2 % to 14 % at angle and from 3 % to 51 % at angular velocities amplitudes outcome in comparison with the left hand.
Angles, angular velocity, angular acceleration of appropriate motion used in dynamic model (Fig. 2) mathematical Eq. (2) for joint torque values calculation at the UE motion (Fig. 1). Torque values expressed in generalized coordinate (angle) domain in range of motion. Thus all 23 participant expressions received at specific movement and mean of the values were calculated. Finally, least squares method applied to approximate mean torque values in an angle domain by using a 3rd degrees polynomial. From all participant’s UE motions measurements obtained torques in angle domain are represented by characteristic equations (Table 1.).
Table 1Characteristic torques Mi equations in angle domain θ at appropriate UE motion
Side | Joint | Motion | Torques characteristic equation |
Left | elbow | flexion | |
Right | elbow | flexion | |
Left | shoulder | flexion | |
Right | shoulder | flexion | |
Left | shoulder | extension | |
Right | shoulder | extension | |
Left | shoulder | adduction | |
Right | shoulder | adduction | |
Left | shoulder | abduction | |
Right | shoulder | abduction |
Work and power as objective dynamic parameters of performed UE motions of healthy people were calculated (Fig. 4). Work done during the motion was calculated by integration of characteristic equation in range of motions which is the difference between motion angle amplitude and initial position. Power was calculated as work done divided by duration of that motion .
Fig. 4Shoulder (Sh) and elbow (El) motion’s characteristic work and power values and it’s SD at appropriate motions: flexion (flex), extension (ext), adduction (add), abduction (abd)
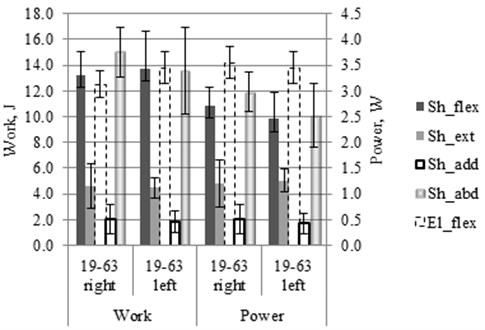
Finally, Pearson’s correlation coefficients () between angles, angular velocities, work and power amplitudes were calculated for experiment’s motions of the left and the right sides. Following values of r were obtained: work and power 0.61-0.99; work and amplitude of angular velocity 0.03-0.39; work and angle amplitude 0.44-0.66; power and angular velocity 0.07-0.58; power and angle amplitude 0.28-0.68; angular velocity and angle amplitude 0.49-0.82.
5. Conclusions
The dynamic and kinematic outcomes have big enough SD of the parameters. It shows that it is always possible to measure appropriate individual motion quality result that could differ from the average of healthy people. Calculated parameter’s scattered between the same motions because of distinction of the participants (Intrapersonal case). However, patients with affected UE function could be measured by introduced method and their motion’s parameters could be compared to the mean values of healthy people UE motion’s kinematic and dynamic parameters.
Strong correlation rates between angle and angular velocity amplitudes (0.49-0.82) shows that one of kinematic parameters could be enough to evaluate movements quality and it would be better to use angle amplitudes because of lower SD. In that way it would be more reliable to compare healthy people angle’s mean values with the same angle results of disabled people at the appropriate motions. Strong correlation (0.61-0.99) between work done and power during the motion shows that one of that parameters could be used for the same motion quality evaluation and previous studies [24] shows that power is a more important parameter than work for quantitative movement evaluation because power includes time of motion that helps to show better the impact of rehabilitation effect. Observed low correlation between power and angle amplitudes could indicate the fact that it is two different parameters for motion evaluation that complement each other.
The motion’s quality evaluation with proposed method before and after rehabilitation could be more reliable by examining movements of the same patient (Interpersonal case) because previous studies showed [24] it helps to remove the distinction of different patients. Anyway, the proposed method shows a possibility before the existed quantitative motion evaluation only by kinematic data to extend by dynamic parameters as well.
References
-
Wade D. T. Measurements in neurological rehabilitation. Current Opinion in Neurology, Vol. 5, Issue 5, 1992, p. 682-686.
-
Nakayama H., Jorgensen H., Raashou H., Olsen T. Compensation in recovery of upper extremity function after stroke: The Copenhagen strike study. Archives of Physical Medicine and Rehabilitation, Vol. 75, 1994, p. 852-857.
-
Arnaldo G., Bruno F., Marcelo A., Ronald N., Elmanto L., Lucas M. Comparative study between physical examination, electroneuromyography and ultrasonography in diagnosing carpal tunel syndrome. Brasil Journal of Orthopedics, Vol. 49, Issue 5, 2013, p. 446-451.
-
Sluys K. P., Shults J., Richmond T. S. Health related quality of life and return to work after minor extremity injuries: a longitudinal study comparing upper versus lower extremity injuries. Injury, Vol. 47, Issue 4, 2016, p. 824-831.
-
Yang N., Zhang M., Huang C., Jin D. Motion quality evaluation of upper limb target reaching movements. Medical Engineering and Physics, Vol. 24, Issue 2, 2002, p. 115-120.
-
Van Tuijl J., Janssen Potten Y., Seelen H. Evaluation of upper extremity motor function tests in tetraplegics. Spinal Cord, Vol. 40, 2002, p. 51-64.
-
Jebsen R. H., Taylor N., Trieschman R. B., Trotter M. J., Howard L. A. An objective and standardized test of hand function. Archives of Physical Medicine and Rehabilitation, Vol. 50, Issue 6, 1969, p. 311-319.
-
Fugl-Meyer A. R., Jaasko I., Leyman I., Olsson S., Steglind S. The post-stroke hemiplegic patient. A method for evaluation of physical performance. Scandinavian Journal of Rehabilitation Medicine, Vol. 7, Issue 1, 1974, p. 13-31.
-
Boyce W., Gowland C., Rosenbaum P., Lane M., Plews N., Goldsmith C., Russel D. Measuring quality of movement in cerebral palsy: a review of instruments. Physical Therapy, Vol. 71, 1991, p. 813-819.
-
Mahoney F. I. Functional evaluation: the Bartel index. Maryland State Medical Journal, 14, p. 61-65.
-
Keith R. A. The functional independence measure: a new tool for rehabilitation. Advanced Clinical Rehabilitation, Vol. 2, 1987, p. 6-18.
-
Catz A., Itzkovich M., Agranov E., Ring H., Tamir A. SCIM – spinal cord independence measure: a new disability scale for patients with spinal cord lesions. Spinal Cord, Vol. 35, Issue 12, 1997, p. 850-856.
-
Burdet E., Milner T. Quantization of human motions and learning of accurate movements. Biological Cybernetics Journal, Vol. 78, 1997, p. 307-318.
-
Woodworth R. S. The accuracy of voluntary movement. Psychological Review Monograph Supplements, Vol. 3, Issue 3, 1899, p. 5-12.
-
Fitts P. M. The information capacity of the human motor system in controlling the amplitude of movement. The Journal of Experimental Medicine, Vol. 47, 1954, p. 381-391.
-
Kondraske G. V. An angular motion Fitts’ law for human performance modelling and prediction. IEEE Engineering in Medicine and Biology, Vol. 1, 1994, p. 307-308.
-
Reyes-Guzman A.,Gil-Agudo A.,Penasco-Martin B.,Solis-Mozos M.,Ama-Espinosa A.,Perez-Rizo E. Kinematic analysis of the daily activity of drinking from a glass in a population with cervical spinal cord injury. Journal of Neuroengineering and Rehabilitation, Vol. 7, Issue 41, 2010, p. 1-12.
-
Murphy M. A., Sunnerhagen K. S., Johnels B., Will C. Three-dimensional kinematic motion analysis of a daily activity drinking from a glass: a pilot study. Journal of Neuroengineering and Rehabilitation, Vol. 3, Issue 18, 2006, p. 1-11.
-
Murphy M. A., Johnels B., Will C., Sunnerhagen K. S. Kinematic variables quantifying upper extremity performance after stroke during reaching and drinking from a glass. Neurorehabilitation and Neural Repair, Vol. 25, Issue 1, 2011, p. 71-80.
-
David A. W. Biomechanics and Motor Control of Human Movement. Fourth Edition. John Whiley and Sons, Waterloo, Ontario, Canada, 2009.
-
Windolf M., Gotzen N., Morlock M. Systematic accuracy and precision analysis of video motion capturing system – exemplified on the Vicon-460 system. Journal of Biomechanics, Vol. 41, 2008, p. 2776-2780.
-
Yang P. F., Sanno M., Brugemann G. P., Rittweger J. Evaluation of the performance of a motion capture system for small displacements recording and a discussion for its application potential in bone deformation in vivo measurements. Journal of Engineering in Medicine, Vol. 226, Issue 11, 2012, p. 838-847.
-
Land W. M., Volchenkov D., Blassing B. E., Schack T. From action representation to action execution: exploring the links between cognitive and biomechanical levels of motor control. Frontiers in Computational Neuroscience, Vol. 7, Issue 127, 2013, p. 1-14.
-
Linkel A., Daunoraviciene K., Griskevicius J., Juocevicius A., Raudonyte I. Application of inertial sensors in medicine: towards model based rehabilitation. IFAC-PapersOnLine, Vol. 48, Issue 5, 2015, p. 442-447.
About this article
Special thanks for Coventry University (UK) Professor Dr. J. Shippen and Dr. B. May for the support during the experiment with motion capturing system and the internship.
