Abstract
The article describes a vibro-mechanical method of residual stress relaxation in long-length parts of the “shaft” type. The method is based on creation and uniform motion of plasto-elastic deformation zone generated by the bending moment at continuous rotation of the part. This leads to occurrence of the high-cyclic loading. Under controlled high-cyclic loading there occur accumulation and subsequent relaxation of residual stresses. The process of vibro-mechanical residual stress relaxation is described by a mathematical model which establishes relation between the geometrical, physical-mechanical and process-dependent parameters. The mathematical model is based on the energy approach to the description of plasto-elastic deformation of a part at high-cyclic loading. The results of experiments with the application of the presented model are given in graph form. They describe the dependence of the residual stress values on the duration of vibro-mechanical processing.
1. Introduction
Long-length cylindrical parts with small diameter are slender parts of the “shaft” type. These shafts are often used in machines during torque transfer and subjected to high-cyclic dynamic loads. After some time, the presence of residual stresses and non-straightness of the shaft geometrical axis lead to an increase of the vibrational amplitude of the shaft, its subsequent failure and the breakage of the whole machine. Therefore, the quality of slender shafts should meet the strict requirements.
The technological process of slender shafts manufacturing is accompanied by accumulation of internal stresses occurring in every thermal and mechanical operation. Therefore, to reduce the residual stresses tempering is applied. It is conventionally performed by heating and subsequent slow cooling of a part. Because of its physical nature thermal tempering does not provide a complete and uniform relaxation of residual stress, resulting in subsequent deterioration of the shape and the need for correction. Along with this, thermal tempering is characterized by high power consumption and poor efficiency [1, 2].
In order to solve the assigned problem, a method of residual stress relaxation of long-length slender parts was developed based on the application of vibro-mechanical energy [3-5].
2. A method of vibro-mechanical stress relaxation
A method for correction and stabilization of long-length cylindrical parts using the moving bending moment were described [6]. We studied the mechanism of this process, performed its mathematical modelling, developed an algorithm and a program for computer simulation of the studied process and analysed the obtained results.
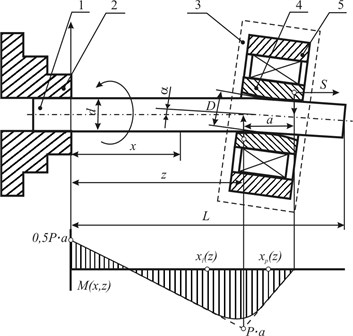
The diagram of the method for correction and stabilization of parameters of cylindrical parts is shown in Fig. 1.
The end of cylindrical workpiece 1 with the diameter and length is rigidly fixed in the machine chuck 2. Tool 3 is fed to the surface of the workpiece at the closest distance to chuck 2. The tool is made in the form of a bushing 4 with the possibility of a free rotation in the bearing of the holder 5. Symmetry axis of tool 3 is inclined to the axis of workpiece 1 so that bushing 4 with its rounded edges bends the workpiece at an angle . Tool 3 is set so that the axis of the workpiece coincides with the rotation axis of chuck 2. Under the influence of the workpiece 1 bending at the angle between the edges of the bushing 4 and the workpiece 1 there occurs a couple of forces , which leads to the bending moment in arbitrary cross-section . This moment depends on the position of tool 3. The angle is chosen so that the plastic deformation appears in the cross-section of the workpiece where it contacts the rollers:
where is the yield point of the part material, MPa; is the bending section modulus, mm3; and the radius of the rollers profile is chosen so that the plastic strain also occurs on the workpiece surface.
To perform the machining, workpiece 1 is put into rotation by chuck 2 with the set frequency , while the tool is moved along the part axis with the feed . Machining finishes when bushing 4 stops contacting workpiece 1.
The technical result comprises the correction of errors in geometric shape of the workpiece, stabilization of its geometrical parameters in time, strengthening of the surface layer and decrease of the surface roughness.
Fig. 1The diagram of the processing method
3. The model of vibro-mechanical stress relaxation
To determine the required values of technological parameters a mathematical model describing the vibro-mechanical relaxation of residual stresses was developed.
In the mathematical model the following was hypothesized:
1. The application point of the bending moment is always on the rotation axis of a part.
2. In the piece during the vibro-mechanical loading some part of the energy spent on the workpiece deformation is absorbed by defects in the workpiece material, which cause residual stress. This energy is absorbed in proportion to potential energy occurring as a result of residual stresses:
where is the potential energy of residual stresses, acting in the material of the workpiece; is the strain energy of the workpiece during machining; is the saturation energy of the workpiece material with residual stresses, at which the workpiece material may be destroyed; is the part of the strain energy of the workpiece, which is absorbed by its material as a result of the hysteresis.
3. Mechanical properties of the workpiece material are not changed during the processing.
4. The influence of inertial forces, temperature and other physical factors is small so they can be neglected.
For the purpose of relieving residual stresses, it is necessary to create a moving plastic deformation zone, which evenly passes along the axis of rotation of all the part and results in a uniform relaxation of residual stresses. In order to create the zone of transition from elastic strain into the plastic one, as it was specified in the works of Birger I. A. [7, 8], the bending moment is defined by the following expression:
where is the diameter of the workpiece; is the distance from the section centre of the workpiece, which corresponds to the transition of elastic strain into the plastic one.
Based on expression Eq. (3) the coordinate of the point of elastic/plastic strain transition along axis is defined by expressions:
where and are the coordinates of points of elastic/plastic strain transition from the workholding and from its free end side, respectively; is the dimensionless factor; – the yield point of the material; – the maximum stress of the elastic strain in the part.
Plastic strain of the workpiece material occurs near point x=z and at a distance on the left and on the right. When elastic strain undergoes in the rest part of the strain zone. If the plastic strain exceeds residual strain of the workpiece material, the intrinsic error of the workpiece is eliminated, however, there occurs new strain.
In the course of plastic strain in the workpiece specific energy is spent in every point of its outer surface at a fixed angular position. This energy is defined by the expression below if the tool support moves helically relative to the rotation axis of the part at an arbitrary section per one cycle of the workpiece:
where is the elasticity modulus of the workpiece material; is the cross-sectional moment of inertia of the workpiece relative to the neutral axis; is the specific energy of plastic strain of the workpiece in an arbitrary section ; is the tool advance; is the angle of rotation of the workpiece around its axis; ; is the dimensionless factor of correction depending on , , .
To relieve the stress caused by the plastic strain it is necessary to apply energy of elastic strain to the workpiece, which equals or exceeds the energy of plastic strain plus the energy of the initial residual stresses in the workpiece. Specific energy of elastic strain in -section at an arbitrary position of the tool in the zone per one rotation of the workpiece can be found by analogy with expression Eq. (5):
where is the arbitrary angular position of the workpiece.
If before processing in the section of the workpiece there were stresses causing the internal modulus of resilience , some part of this energy is absorbed by the workpiece material during the plastic strain and there remains the modulus of resilience equal to:
where is the residual modulus of resilience in the workpiece material in section after plastic strain.
After the -stroke of elastic strain part of this energy Eq. (7) will be absorbed by the elastic strain energy and the workpiece will have the energy equal to:
where is the number of strokes of the elastic strain.
In accordance with expression Eq. (5) for the residual bending moment and the residual stress in -section, the differential equation of the elastic curve is defined by:
In the integrated form with zero initial conditions expression Eq. (9) takes the following form:
As it can be seen from the above expressions, the dependence of the workpiece strain on the influencing factors has a complex implicit character; however, it allows us to define the process parameters of vibro-mechanical processing with the help of computer-aided design.
4. Experimental research
As an example, let us consider vibro-mechanical processing of a cylindrical shaft made of steel 70 (2.1∙105 MPa; 8.5∙104MPa; 735 MPa) with diameter 4 mm and the working length 120 mm 12.5 mm2; 6.28 mm3, 12.5 mm4). Vibro-mechanical processing of a part is performed with the frequency 90 min-1.
During the experiment time of the processing and bending moment, which defines generated internal stresses, were taken as variable parameters.
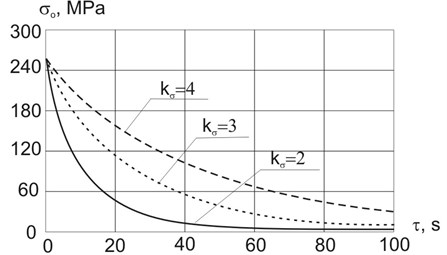
According to the results of the experiment, Fig. 2 represents a dependency graph of residual stresses on the needed time for the processing , reverse to the feeding value: . The needed processing time means the time required for a complete relaxation of residual stresses since the beginning of the processing. The graph in Fig. 2 shows that the increase in external load, which conditions the value of the maximum stress of elastic strain of the part inversely proportional to the factor , leads to a reduction of the required processing time
From the graph in Fig. 2 it can be seen that the lower the factor the higher the stresses occurring in the product during the vibro-mechanical processing, and the lower the time required for the relaxation of residual stresses.
Fig. 2The dependence of the residual stresses in the part σokσ,τ on the processing time at different ratios of value kσ= {2, 3, 4}
5. Conclusions
The studies of the developed method for vibro-mechanical stabilization of geometrical parameters of long-length slender parts allowed confirming its efficacy in comparison to the method of thermal tempering, and establishing the dependence of the processing time required for the complete relaxation of residual stresses on the process of bending moment conditioning stresses of elastic strain. The resulting mathematical model can be used to calculate the technological parameters of vibro-mechanical processing of long-length parts in order to reduce the magnitude of residual stresses and strains. According to the results of the experiment, it was revealed that an increase in the technological bending moment allows the reduction of the time of the vibro-mechanical processing.
References
-
Hsieh C. C., Lai C. H., Wu W. Effect of vibration on microstructures and mechanical properties of 304 stainless steel GTA welds. Metals and Materials International, Vol. 19, Issue 4, 2013, p. 835-844.
-
Wang J. S., Hsieh C. C., Lin C. M., Kuo C. W., Wu W. Texture evolution and residual stress relaxation in a cold-rolled Al-Mg-Si-Cu alloy using vibratory stress relief technique. Metallurgical and Materials Transactions A, Vol. 44, Issue 2, 2013, p. 806-818.
-
Djuric D., Vallant R., Kerschbaumer K., Enzinger N. Vibration stress relief treatment of welded high-strength martensitic steel. Welding in the World, Vol. 55, Issue 1, 2011, p. 86-93.
-
Chuvas T. C., Castello D. A., Cindra Fonseca M. P. Residual stress relief of welded joints by mechanical vibrations. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2016, p. 1-9.
-
Vardanjani M. J., Ghayour M., Homami R. M. Analysis of the vibrational stress relief for reducing the residual stresses caused by machining. Experimental Techniques, Vol. 40, Issue 2, 2016, p. 705-713.
-
Korolev A. V., Korolev A. A., Balayev A. F., Savran S. A., Yakovishin A. S. Method of Straightening of Long Parts. Patent 2581692 RU 11, 2016.
-
Birger I. Residual Stresses. Mashgiz, Moscow, p. 1963-232.
-
Birger I., Shorr B., Iosilevich G. Calculation of the Strength of Machine Parts: Directory. Mechanical Engineering, 1993, p. 640.
About this article
This work was executed at financial support of the Ministry of Education and Science of the Russian Federation, Agreement No. 9.896.2014/K.
