Abstract
A hypothesis about thermomechanical nature of self-oscillations during metal machining is offered, that provides performing generalization of main known models of this phenomenon. Basing upon the offered hypothesis the analytic and digital models of self-oscillations actuations were developed. Adequacy of obtained results is confirmed by results of full-scale experiments.
1. Introduction
Self-oscillations emerging during metal machining are the main limiters of productivity and accuracy of processing on metal-cutting machine tools. Many Russian and foreign researchers were engaged in search for physical causes of self-oscillations beginning during metal machining. A great number of this procedure models were developed. The suggested models can be conditionally divided into two large groups. The first group of such models is based upon static or dynamic two-valued property of the cutting force, and cause isolation of this two-valued property is performed using single-degree-of-freedom systems. The most widespread models that belong to this group are: a model based upon cutting force decreasing with speed [1]; a model based upon cutting force ambiguousness during downcutting and repulsion of the cutting tool [2]; a model based upon retardation of cutting force change from change of a layer thickness [3]. All theories known to us as belonging to this group are based on regularities observed experimentally, but they do not open real physical causes of these phenomena and do not provide predicting a level of vibration during the cutting. To the second group we can refer those theories that are based on presentation of a technological system in a form of two or more degrees of freedom, where self-oscillations are explained by an availability of coordinate connection between them [4-7]. This phenomenon is studied sufficiently well. The mathematical models are already formed and the methods of struggle against such type of self-oscillations are developed. But the principle of coordinate connection cannot explain self-oscillations actuation in twisting systems and in systems with one degree of freedom. On metal-cutting machine tools the twisting systems are widely used, and the systems with one degree of freedom are frequently met when working with symmetrically arranged edges, i.е. when performing drilling, hole enlarging, pulling through etc. operations. These speculations suggest an idea about existence in technological systems of a physical principle responsible for actuation of self-oscillations, depicted by models with one degree of freedom.
2. Physical principle of thermomechanical oscillation
Attentive consideration of existing models of self-oscillations when cutting with one degree of freedom [1-3] suggests a thought, that phenomena, laying in their foundation, are the results of a unique deep physical principle. Disclosure of this principle will provide more deep understanding of the nature of self-oscillations during cutting and to offer methods of struggle against this phenomenon.
Consideration of connections between mechanical and thermodynamic processes, taking place during metal cutting, permitted suggesting a hypothesis about thermomechanical nature of self-oscillations during cutting.
The cutting forces arising during the cutting process are created mainly by means of plastic deformation of a cutted layer of the half-finished article material and overcoming of friction forces on the operational surfaces of the working tool. The mechanical energy, spent on plastic deformation of half-finished article material and friction between surfaces of a tool, cutting waste and the product is converted into heat energy that results in essential increase of the cutting zone temperature [8]. At increasing temperature of the half-finished article material some structural conversions take place, and, as a result, mechanical properties of the processed material, such as elasticity modulus, flexural yield stress and limit of the ultimate strength become changed, that in its turn results in change of cutting force. Thus, mechanical and heat processes taking place during cutting, become continuously connected each with other and interdependent each from others.
A majority of metals processed by cutting has a drooping dependence of their mechanical characteristic upon temperature as their distinctive feature. The cutting force directly depends on the limit of the ultimate strength of the processed material and in the first approximation is proportional to it. Consequently, dependence “cutting force – temperature” also has a negative angle of slope that determines potential instability of the system, and, as a consequence, has a possibility of emergence of self-oscillations in it.
3. Mathematical model of thermomechanical oscillation
Let us consider a dynamic model shown in Fig. 1, in which the cutting force is a known steadily decreasing function on the temperature in the cutting zone.
Fig. 1A model of self-oscillating system
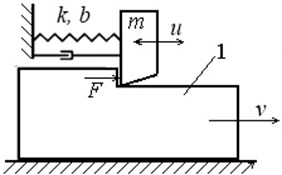
An equation of the cutting tool oscillations has the form:
For calculation of temperature in the cutting zone let us write an equation of energy balance connecting change of temperature in the cutting zone with mechanical energy converted into the heat energy and the heat released into ambient medium:
where is the ambient medium temperature; is the heated mass; is the specific heat capacity; is the coefficient of heat transfer.
The system of Eq. (1), (2) has a particular solution corresponding to steady equilibrium state , .
From Eq. (1) let us find a position of a cutting tool in the steady state:
where , and the equilibrium temperature is found by solving the following equation derived from the Eq. (2):
Now let us go over to estimation of stability of the found equilibrium condition. With this purpose let us introduce the new coordinates and , describing small deviations of the coordinate and temperature from the above obtained stationary values and let us carry out linearization of the cutting force dependence on the temperature in vicinity of these values.
where .
In the result from the Eq. (1), (2), taking into account Eq. (3), (4), having limited by values of the first order of smallness, we obtain equations describing small oscillations with respect to equilibrium position:
From Eq. (6) we find:
After substitution Eq. (3) into Eq. (2) we shall obtain on rearrangement the following equation with respect to :
where , , ,
Let us write characteristic Eq. 9:
where , , , .
In accordance with Routh-Gurvitz criteria for the system stability described by the third order equation, except for positive coefficients of the characteristic Eq. (9) it is necessary to provide fulfillment of the condition , which, taking into the account the accepted designations, takes the form:
First of all, we are concerned in the case of drooping characteristic of the cutting force, at which the derivative , and according to designations adopted in Eq. (8) . In this case in the Eq. (9) the coefficients , , and for the provision of stability except for condition Eq. (10) it is necessary to require fulfillment of the inequality . It is easy to show, that this inequality is weaker than the condition Eq. (10). Really, if we shall state , then the left part of the inequality Eq. (1) becomes equal to zero and, consequently, the inequality is violated, i.е. destabilization takes place and self-oscillations are actuated. Thus, for estimation of stability and building a boundary of stability loss area it is necessary to use the inequality Eq. (10). In absence of dissipation in the oscillatory system, i.е. at the inequality Eq. (10) is violated and self-oscillations are actuated at any value (or 0). The considered model is built at certain assumptions. It is assumed that heating at cutting takes place uniformly in a certain volume, having the mass , and transfer of heat into the medium takes place through a boundary of sharp temperature difference. From exploration of temperature processes, accompanying metal cutting, it is known, that a zone of highest temperatures is really situated in a sufficiently narrow vicinity of the cutting tool contact with a half-finished article, and change of temperatures during dissipation of heat into a medium takes place with sufficiently high gradient. Analytic solution of a redetermined model of this process is hardly possible. Therefore, further study of thermomechanical self-oscillations was performed using digital methods.
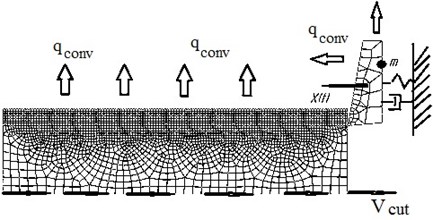
4. Finite-element model
A two-dimensional finite-element model is shown in Fig. 2. During its constructing we used an ideal elastoplastic model made of material, which elasticity modulus and limit of stretching strain depend upon temperature. The tool is simulated as an oscillatory system with one degree of freedom. The friction between the tool, a half-finished article and a cutting waste is considered to be a Coulomb type. The shear deformation critical value is chosen as the criterion for estimation of chip formation, at which achievement the element is deleted from a mesh.
Fig. 2Boundary conditions of finite element model
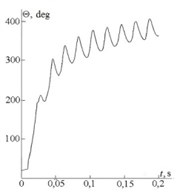
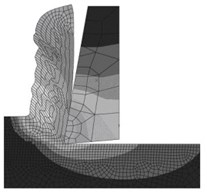
As a result of calculations a possibility of self-oscillations excitation was confirmed. Both transition and steady-state modes of self-oscillations were obtained. In Fig. 3(a) а change of temperature is shown during a procedure of self-oscillations establishment in the process of a cutting tool downcutting into the material.
It is possible to observe, that at the beginning of cutting the process is accompanied with fast heating of the material, and at temperature of 200 deg. generation of self-actuated oscillations takes place further transfer to steady-state condition of self-oscillations with amplitude of temperature oscillations about 40 deg. in vicinity of average temperature about 400 deg. takes place as a consequence of non-linear temperature dependence of material mechanical characteristics upon temperature.
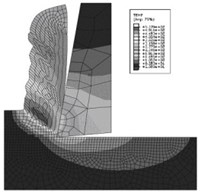
Fig. 3Distribution of temperatures in a cutting zone in opposite phases of oscillations
a)
b)
c)
In Fig. 3(b), (c) the pictures of temperature distributions are given in the cutting zone in two phases of cutting tool oscillations in a steady-state mode: а) at a moment when maximal value of temperature is achieved; b) at a moment when minimal value of temperature is achieved. In Fig. 3(b) a local area is distinctly visible with high temperature in the primary zone of shear at formation of cutting waste. Namely assumption about similar localization and presence of a boundary of sharp temperature difference with ambient medium was one of basic assumptions adopted during mathematical model Eqs. (1), (2) constructing.
Study of a given model permits performing the impact analysis of processed material properties, technological system parameters and cutting conditions onto nature and level of vibration during metal cutting processes. We have found stability boundaries, and investigated influence of self-oscillations onto shape of the chip, as well as studied influence of thermomechanical properties of the processed material onto the nature and intensity of vibration.
In the result of simulation, we determined laws of changing in time for main parameters of self-oscillation process. An example of solution is shown in Fig. 4.
Fig. 4Graphic charts of main parameters changing in time for steady state self-oscillating process
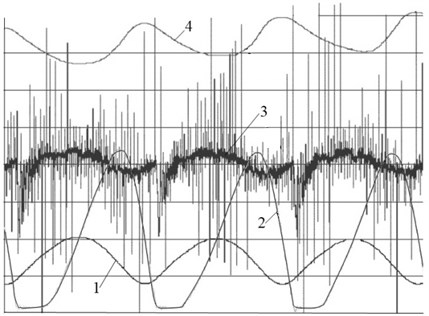
Here: 1 is a curve of cutting tool oscillations; 2 is a curve for the cutting tool speed with respect a half-finished article moving at a constant speed; 3 is a curve for the cutting force; 4 is a curve for the temperature in a contact zone for the cutting tool and the cutting waste.
Oscillations of the cutting tool take place at a frequency of elastic system self-oscillations according to a law close to harmonic (curve 1). But relative speed of the cutting tool has a segment, where this speed is equal to zero, i.e. the cutting tool is immovable with respect to a half-finished article and its speed in absolute motion is equal to a speed of the product. During the mutual motion the energy from a drive of a half-finished article is saved by the cutting tool elastic system, and then, when the force of a spring will be sufficient for overcoming the cutting resistance, a countermotion of the cutting tool begins. From comparing a chart of relative speed with a chart of temperature changing (curve 4) it is seen, that for motion in the same direction and relative stop of motion the temperature in the cutting zone decreases, and during the countermotion it increases. Namely such change of temperatures creates conditions for emergence and support of self-oscillations.
Special attention should be given to a chart of cutting force dependence from time (curve 3). The cutting force on the average follows the change of temperature, but its chart comprises additional high-frequency components. It seems likely that they are consequences of discontinuity of the contact line connecting the cutting waste and a half-finished article. Correctness of this assumption is confirmed by the fact that the frequency of such high-frequency oscillations is approximately equal to the frequency of destruction of finite elements on the contact line. A certain contribution into the overall picture of cutting force oscillations are made by elastic oscillations of the cutting waste.
It is interesting to pay attention onto an indicative gap observed on the chart on the boundary of transition to a segment of relative stop of the cutting tool. This gap is explained by passage of segments where elastic unloading and loading take place in the cutting zone at transfer from plastic deformation to elastic loaded condition and vice versa.
5. Conclusions
Investigation of finite-element model of cutting tool self-oscillations provided checking the correctness of an assumption about thermomechanical nature of self-oscillations during the cutting and adequacy of this process mathematical model. The type of obtained results is in agreement with results of natural experiments [9]. Created models can serve for finding cutting modes, providing minimal level of vibrations, as well as during designing metal-cutting tools and furniture. Understanding of physical mechanism of self-oscillations excitation as an interdependent thermomechanical process allows making clear physical sense of phenomena, being fundamental for the most commonly encountered models of self-oscillations during the cutting [1-3]. At present time an experimental work is carried out on checkout of adequacy for the thermomechanical model of self-oscillation excitation during the cutting, consisting in full-scale study of vibratory displacement fields, temperature fields and deformation fields emerging during self-oscillations.
References
-
Kashirin А. I. Investigation of Vibrations during Metal Cutting. USSR Academy of Science, Мoscow-Leningrad, 1944, p. 282, (in Russian).
-
Sokolovskiy А. P. Vibrations if Operating at Metal-Cutting Machine Tools. Investigation of Metal-Cutting Machine Tool Oscillations during Metal Cutting. Machine Designing Publication Office, Мoscow, 1958, (in Russian).
-
Elyasberg М. Е. Basics of Self-Oscillation Theory in Metal-Cutting Industry. Russian Engineering Research, Nos. 10-11, 1962, (in Russian).
-
Kudinov V. А. Dynamics for Machine-Tools. Mashinostroenie, Мoscow, 1967, p. 360, (in Russian).
-
Tlustyj I. Self-Oscillations in Metal-Cutting Machine-Tools. Machine Designing Publication Office, Мoscow, 1956, (in Russian).
-
Wang Z. C., Cleghor W. L., Yu S. D. Chatter in Tuming process incorporating the effect of ploughing force. Proceeding of the ASME, 1999.
-
Wang Zhanchen Chatter Analysis of Machine Tool Systems in Turning Processes. Ph.D. Thesis, Department of Mechanical and Industrial Engineering University of Toronto, 2001, p. 229.
-
Granovskiy G. I., Granovskiy V. G. Metal Cutting. Visshaya Shkola, Мoscow, 1985, p. 304, (in Russian).
-
Zharkov I. G. Vibrations During Processing by Edge Tools. Mashinostrojenije, Leningrad, 1987, p. 184, (in Russian).
About this article
The study was performed account for a grant the Russian Science Foundation (Project No. 15-19-30026).
