Mathematical modeling of hydroelastic walls oscillations of the channel on Winkler foundation under vibrations

Mogilevich, Lev I.; Popov, Victor S.; Popova, Anna A.; Christoforova, Aleftina V.

Vibroengineering Procedia

Browse Procedia

Published: 07 October 2016

Check for updates

Mathematical modeling of hydroelastic walls oscillations of the channel on Winkler foundation under vibrations

Lev I. Mogilevich¹

Victor S. Popov²

Anna A. Popova³

Aleftina V. Christoforova⁴

^{1, 2, 3}Yuri Gagarin State Technical University of Saratov, Saratov, Russia

⁴Saratov State University, Saratov, Russia

Corresponding Author:

Victor S. Popov

Cite the article Download PDF

Downloads 1228

Abstract

The bending oscillations of a narrow slit channel walls with highly viscous liquid inside and put on a vibrating Winkler foundation are investigated. The channel walls bending oscillations laws are discovered on the basis of hydroelasticity problem solution, as well as pressure in the liquid ones. The deflections amplitudes distribution and liquid pressure along the channel functions are constructed. The obtained results allow investigating dynamic processes, conditioned by constructions elastic elements and viscous liquid interaction in lubrication system, damping and various devices and units.

1. Introduction

The elastic elements of constructions with liquid oscillations are of great importance for modern machines, units and devices analysis [1]. In reference [2] the rectangular plate oscillations plunged into an ideal incompressible liquid with a free surface are investigated. Reference [3] studies the plate chaotic oscillations under interaction with ideal incompressible flow. The problem of round plate oscillations on incompressible liquid fee surface is considered in reference [4], whereas reference [5] investigates round plate oscillations in water with free surface. The problem of bending oscillations of channel wall interacting with ideal liquid, which fills the channel, is solved in [6], and vibration cavitations in cooling liquid, surrounding internal-combustion engine shell having been solved on its basis. The investigation of the beam hydroelastic oscillation in viscous flow with application to piezoelectric element which can be used for receiving energy from the flow is made in [7]. Reference [8] studies the cantilevering fixed beam oscillations in an unlimited volume of viscous incompressible flow. Reference [9] investigates interminable plate oscillations on viscous liquid layer. The investigation of terminable length vibrating plates interaction with viscous incompressible liquid layer between them is made in [10]. References [11, 12] consider analogues problems for round disks with one of them being three-layered. The plate oscillations, caused by pressure pulsating in viscous liquid layer are considered in [13]. References [14, 15] deal with three-layered plates interaction with viscous liquid layer. The oscillations of membrane with elastic foundation, situated on the channel bottom, with ideal incompressible liquid with a free surface inside the channel are investigated in [16]. However, for practical purposes, the consideration of thin liquid layer viscosity impact on elastic channel walls oscillations, for the case of the channel having vibrating elastic foundation, is of great interest.

2. Statement of the problem

Let us consider a narrow slit channel, filled with highly viscous incompressible liquid (see Fig. 1). The channel walls make two elastic plates 1 and 2, being of similar geometrical sizes in the plan and simply supported at the butt ends. The channel size $b ≫ l$ . The plates thicknesses are $h_{1}$ , $h_{2}$ , the liquid layer thickness is $δ_{0} ≪ l$ . The plate 1 is put on Winkler elastic foundation. The considered mechanical system performs harmonic oscillations with assigned vibro-acceleration ${\ddot{z}}_{0} = E_{z} d^{2} f_{0} (ω t) / d t^{2} = - E_{z} ω^{2} f_{0} (ω t)$ , $f_{0} (ω t) = s i n ω t$ . Here $E_{z} ω^{2}$ is the vibro-acceleration amplitude, $ω$ is the oscillation frequency, $t$ is the time. The vibro-acceleration amplitude can be assigned in gravity acceleration units $g$ , i.e. $E_{z} ω^{2} = k g$ , here $k$ is the vibro-overloading coefficient. Plates 1, 2 perform bending oscillations with amplitudes $w_{1 m} ≪ δ_{0}$ , $w_{2 m} ≪ δ_{0}$ . In the considered assignment, the liquid flow in the channel is viewed as a creeping one and liquid leakage at the butt ends being free in the same liquid with constant pressure $p_{0}$ .

Fig. 1A schematic diagram of a narrow slit channel on Winkler foundation

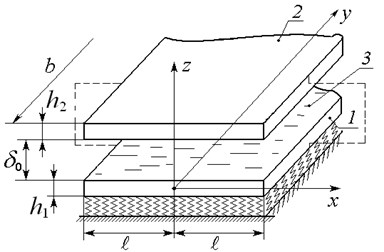
Let us put Cartesian coordinate system in the middle plate 1 surface center. Taking into account, that $b ≫ l$ we will consider the problem in a flat setting. Strong damping, conditioned by liquid viscosity, takes place in the considered oscillating system. Therefore, transition processes in the system will get out rapidly and the stationary oscillations will emerge. Further, according to reference [17], we will focus on studying stationary forced harmonic oscillations regime.

3. The theory

The channel wall bending oscillations equations take the form of:

1

D_{i} \frac{\partial^{4} w_{i}}{\partial x^{4}} + (2 - i) χ w_{1} + ρ_{i} h_{i} ({\ddot{z}}_{0} + \frac{\partial^{2} w_{i}}{\partial t^{2}}) = (- 1)^{i - 1} q, i = 1, 2,

where $w_{i}$ is the deflection of $i$ th plate, $D_{i}$ is the bending stiffness of $i$ th plate, $ρ_{i}$ is the density of $i$ th plate, $χ$ is the elastic coefficient of Winkler foundation, $q = - p + 2 ρ ν \partial u_{z} / \partial z$ is the normal stress, acting from the liquid layer on the plate [18], $p$ is the pressure, ρ is the density of the liquid, $ν$ is the kinematical coefficient of the liquid viscosity, $u_{z}$ is the liquid velocity vector project on coordinate axis $z$ .

Boundary conditions for Eq. (1) are the conditions of simply supported edges:

2

w_{i} = \frac{\partial^{2} w_{i}}{\partial x^{2}} = 0, x = \pm l, i = 1, 2 .

Highly viscous incompressible liquid dynamics in a narrow slit channel is described by Navier-Stokes equations and continuity equation, in which local and convective inertia members are omitted, according to hydrodynamic lubrication theory [18]:

3

\frac{1}{ρ} \frac{\partial p}{\partial x} = ν (\frac{\partial^{2} u_{x}}{\partial x^{2}} + \frac{\partial^{2} u_{x}}{\partial z^{2}}), \frac{1}{ρ} \frac{\partial p}{\partial z} = - {\ddot{z}}_{0} + ν (\frac{\partial^{2} u_{z}}{\partial x^{2}} + \frac{\partial^{2} u_{z}}{\partial z^{2}}), \frac{\partial u_{x}}{\partial x} + \frac{\partial u_{z}}{\partial z} = 0,

where $u_{x}$ is the liquid velocity vector project on coordinate axis x.

Boundary conditions for Eq. (3) are the conditions of liquid adhesion to the walls and the conditions for pressure at the both ends:

4

u_{x} = \frac{\partial u_{2}}{\partial t}, u_{z} = \frac{\partial w_{2}}{\partial t}, at z = \frac{h {}_{1}}{2} + δ_{0} + w_{2},

u_{x} = \frac{\partial u_{1}}{\partial t}, u_{z} = \frac{\partial w_{1}}{\partial t}, at z = \frac{h {}_{1}}{2} + w_{1},

5

p = p_{0}, at x = \pm l,

where $u_{i}$ is the longitudinal shift of $i$ th plate, $i =$ 1, 2.

Let us introduce dimensionless variables:

6

ξ = \frac{x}{l}, ζ = (z - 0,5 h_{1}) δ_{0}^{- 1}, τ = ω t, u_{z} = w_{2 m} ω U_{ζ}, u_{x} = w_{2 m} ω \frac{U_{ξ}}{ψ},

w_{i} = w_{i m} W_{i}, u_{i} = u_{i m} U_{i}, p = p_{0} + P \frac{ν ρ w_{2 m}^{} ω ψ^{- 2}}{δ_{0}} - ρ {\ddot{z}}_{0} (z - δ_{0} - w_{2} - \frac{h_{1}}{2}),

λ_{i} = \frac{w_{i m}^{}}{δ_{0}} ≪ 1, ψ = \frac{δ_{0}}{l} ≪ 1,

where $ψ$ , $λ_{i}$ are the small parameters, characterizing the problem, $i =$ 1, 2.

By substituting Eq. (6) in liquid dynamic Eq. (3) and the corresponding boundary Eq. (4) and (5), we get:

7

\frac{\partial P}{\partial ξ} = ψ^{2} \frac{\partial^{2} U_{ξ}}{\partial ξ^{2}} + \frac{\partial^{2} U_{ξ}}{\partial ζ^{2}}, \frac{\partial P}{\partial ζ} = ψ^{2} [ψ^{2} \frac{\partial^{2} U_{ζ}}{\partial ξ^{2}} + \frac{\partial^{2} U_{ζ}}{\partial ζ^{2}}], \frac{\partial U_{ξ}}{\partial ξ} + \frac{\partial U_{ζ}}{\partial ζ} = 0,

8

U_{ξ} = ψ (\frac{u_{2 m}}{w_{2 m}}) \frac{\partial U_{2}}{\partial τ}, U_{ζ} = \frac{\partial W_{2}}{\partial τ} at ζ = 1 + λ_{2} W_{2},

U_{ξ} = ψ (\frac{u_{1 m}}{w_{2 m}}) \frac{\partial U_{1}}{\partial τ}, U_{ζ} = (\frac{w_{1 m}}{w_{2 m}}) \frac{\partial W_{1}}{\partial τ} at ζ = λ_{1} W_{1},

9

P = 0 at ξ = \pm 1

.

The normal stress, acting from the liquid layer on the plate, will be written down, as:

10

q = ρ δ_{0} {\ddot{z}}_{0} (ζ - 1 - λ_{2} W_{2}) - p_{0} - ν ρ w_{2 m}^{} ω (ψ^{2} δ_{0})^{- 1} (P - 2 ψ^{2}) \frac{\partial U_{ζ}}{\partial ζ} .

Further, we note that in the considered setting $ψ = o (1)$ , $u_{i m} / w_{2 m} = O (1)$ , $λ_{1} = λ_{2} (w_{1 m} / w_{2 m}) = o (1)$ , and therefore, the member at $ψ$ , $ψ^{2}$ , $λ_{1}$ , $λ_{2}$ in Eq. (7), boundary Eq. (8), (9) and normal stress Eq. (10) can be omitted. As a result, we get liquid dynamic problem in the form of the Eq. (11) and boundary Eq. (12):

11

\frac{\partial P}{\partial ξ} = \frac{\partial^{2} U_{ξ}}{\partial ζ^{2}}, \frac{\partial P}{\partial ζ} = 0, \frac{\partial U_{ξ}}{\partial ξ} + \frac{\partial U_{ζ}}{\partial ζ} = 0,

12

U_{ξ} = 0, U_{ζ} = \frac{\partial W_{2}}{\partial τ} at ζ = 1, U_{ξ} = 0, U_{ζ} = (\frac{w_{1 m}}{w_{2 m}}) \frac{\partial W_{1}}{\partial τ} at ζ = 0,

P = 0 at ξ = \pm 1

.

The solutions of the Eq. (11) with boundary Eq. (12) has the form of:

13

U_{ξ} = \frac{ζ^{2} - ζ}{2} \frac{\partial P}{\partial ξ}, U_{ζ} = \frac{w_{1 m}}{w_{2 m}} \frac{\partial W_{1}}{\partial τ} + \frac{3 ζ^{2} - 2 ζ^{3}}{12} \frac{\partial^{2} P}{\partial ξ^{2}},

P = 12 \int_{1}^{ξ} \int_{}^{} \frac{\partial \tilde{W}}{\partial τ} d ξ d ξ - 6 (ξ - 1) \int_{- 1}^{1} \int_{}^{} \frac{\partial \tilde{W}}{\partial τ} d ξ d ξ, \tilde{W} = W_{2} - \frac{w_{1 m}}{w_{2 m}} W_{1} .

By substituting Eq. (13) in the expression from the normal stress Eq. (10), written down in zero approximation at $ψ$ and $λ_{2}$ , and considering the normal stress in channel walls dynamics Eq. (1), we get integro-differential equations of channel walls hydroelastic oscillations:

14

D_{i} l^{- 4} \frac{\partial^{4} w_{i}}{\partial ξ^{4}} + (2 - i) χ w_{1} + ρ_{i} h_{i} ω^{2} (\partial^{2} w_{i} / \partial τ^{2} + {\ddot{z}}_{0} ω^{- 2} (1 + \frac{(2 - i) ρ δ_{0}}{ρ_{i} h_{i}}))

= (- 1)^{i} (p_{0} + 12 ν ρ w_{2 m}^{} ω (ψ^{2} δ_{0})^{- 1} (\int_{1}^{ξ} \int_{}^{} \frac{\partial \tilde{W}}{\partial τ} d ξ d ξ - (ξ - 1) / 2 \int_{- 1}^{1} \int_{}^{} \frac{\partial \tilde{W}}{\partial τ} d ξ d ξ)) .

With consideration of boundary Eq. (2), (5) we will look for the assigned equations solution in the form of:

15

w_{i}^{} = w_{i m}^{} W_{i} = w_{i m}^{} \sum_{k = 1}^{\infty} (R_{i k}^{0} + R_{i k}^{} (τ)) c o s (\frac{(2 k - 1) π ξ}{2}), i = 1, 2,

here the upper index 0 means the solution, corresponding to static pressure $p_{0}$ .

By substituting Eq. (15) into Eq. (14) and setting the remaining members of Eq. (14) in series of trigonometric functions of longitudinal coordinate $ξ$ and then, equating the coefficients at similar trigonometric functions, we obtain the expression for $R_{i k}^{0}$ :

16

w_{i m} R_{i k}^{0} = (- 1)^{i - 1} 4 p_{0} (- 1)^{k} ((2 k - 1) π)^{- 1} {(D_{i} l^{- 4} {(\frac{(2 k - 1) π}{2})}^{4} + (2 - i) χ)}^{- 1},

and the system of ordinary differential equations for $R_{i k} (τ)$ :

17

w_{1 m} a_{11}^{} R_{1 k}^{} + w_{1 m} a_{12}^{} \frac{d R_{1 k}^{}}{d τ} + w_{2 m}^{} a_{14}^{} \frac{d R_{2 k}^{}}{d τ} = - d_{1} E_{z} ω^{2} \frac{d^{2} f_{0}}{d τ^{2}},

w_{1 m} a_{22}^{} \frac{d R_{1 k}^{}}{d τ} + w_{2 m} a_{23}^{} R_{2 k}^{} + w_{2 m} a_{24}^{} \frac{d R_{2 k}^{}}{d τ} = - d_{2} E_{z} ω^{2} \frac{d^{2} f_{0}}{d τ^{2}} .

Here, it is taken into account that for the stationary harmonic oscillations regime we have $d^{2} R_{i k} / d τ^{2} = - R_{i k}$ and the following symbols having been introduced:

a_{11}^{} = D_{1} l^{- 4} ((2 k - 1) π / 2)^{4} + χ - ρ_{1}^{} h_{1}^{} ω^{2}, a_{12}^{} = 2 K_{k} ω, a_{14}^{} = - a_{12}^{},

a_{22}^{} = a_{14}^{} = - a_{12}^{}, a_{23}^{} = D_{2} l^{- 4} ((2 k - 1) π / 2)^{4} - ρ_{2}^{} h_{2}^{} ω^{2}, a_{24}^{} = a_{12}^{} = - a_{14}^{},

2 K_{k} = 12 ρ ν ψ_{}^{- 2} δ_{0}^{- 1} (2 / ((2 k - 1) π))^{2}, d_{i} = - 4 (- 1)^{k} ((2 k - 1) π)^{- 1} (ρ_{i} h_{i} + (2 - i) ρ δ_{0}) .

By solving the system Eq. (17) for the stationary harmonic oscillations regime we find:

18

w_{i m}^{} R_{i k}^{} = E_{z} ω^{2} (\frac{F_{k} C_{i k} - C_{k} F_{i k}}{F_{k}^{2} + C_{k}^{2}} \frac{d f_{0} (τ)}{d τ} - \frac{F_{k} F_{i k} + C_{k} C_{i k}}{F_{k}^{2} + C_{k}^{2}} \frac{d^{2} f_{0} (τ)}{d τ^{2}}),

here $i =$ 1, 2 for plates 1 and 2, the following symbols having been introduced:

F_{k}^{} = a_{11}^{} a_{23}^{}, C_{k}^{} = a_{12}^{} (a_{11}^{} + a_{23}^{}), F_{1 k}^{} = d_{1}^{} a_{23}^{},

F_{2 k}^{} = d_{2}^{} a_{11}^{}, C_{1 k}^{} = C_{2 k}^{} = a_{12}^{} (d_{1}^{} + d_{2}^{}) .

Considering Eq. (16) and (18), we can present the final expressions for plate deflections as:

19

w_{i} = \frac{p_{0} l^{4}}{D_{i}} \sum_{k = 1}^{\infty} (\frac{4 (- 1)^{k} (- 1)^{i - 1}}{(2 k - 1) π} \frac{c o s ((2 k - 1) π x / (2 l))}{((2 k - 1) π / 2)^{4} + (2 - i) χ l^{4} / D_{i}})

+ E_{z} ω^{2} A_{i} (x, ω) s i n (ω t + ϕ_{i} (x, ω)),

A_{i} = \sqrt{Q_{i}^{2} + N_{i}^{2}}, ϕ_{i} = a r c t g (\frac{N_{i}}{Q_{i}}),

Q_{i} = \sum_{k = 1}^{\infty} \frac{F_{k} F_{i k} + C_{k} C_{i k}}{F_{k}^{2} + C_{k}^{2}} c o s \frac{(2 k - 1) π x}{2 l}, N_{i} = \sum_{k = 1}^{\infty} \frac{F_{k} C_{i k} - C_{k} F_{i k}}{F_{k}^{2} + C_{k}^{2}} c o s \frac{(2 k - 1) π x}{2 l} .

Taking into account Eqs. (18), (15) in the expression for pressure Eq. (13) we finally obtain the law of dimensional pressure distribution in the channel in the form:

20

p = p_{0} - ρ {\ddot{z}}_{0} (z - δ_{0} - \frac{h_{1}}{2}) + E_{z} ω^{2} Π (x, ω) s i n (ω t + ϕ_{p} (x, ω)),

Π (x, ω) = \sqrt{B_{k}^{2} + S_{k}^{2}}, ϕ_{p} (x, ω) = a r c t g (\frac{S_{k}}{B_{k}}),

B_{k} = \sum_{k = 1}^{\infty} 2 K_{k} ω C_{k} \frac{F_{1 k}^{} - F_{2 k}^{}}{F_{k}^{2} + C_{k}^{2}} c o s \frac{(2 k - 1) π x}{2 l},

S_{k} = \sum_{k = 1}^{\infty} 2 K_{k} ω F_{k} \frac{F_{1 k}^{} - F_{2 k}^{}}{F_{k}^{2} + C_{k}^{2}} c o s \frac{(2 k - 1) π x}{2 l} .

4. Conclusions

The first member of the Eq. (19) is the channel walls static deflection conditioned by static pressure in the liquid $p_{0}$ , the second member is the deflection, conditioned by foundation vibration. The first component in pressure distribution law Eq. (20) represents static liquid pressure in the channel. The second component is dynamic liquid pressure, conditioned by foundation vibro-acceleration (an analogue of pressure due to the gravity). The third component is pressure, conditioned by channel walls oscillations under foundation vibro-acceleration.

It must be noted that the first and the second pressure components cannot exceed the assigned values. The third component pressure value is defined by the function $Π (x, ω)$ , which represents pressure distribution frequency dependent function along the channel. Under longitudinal coordinate fixed value $x$ , the assigned function is the pressure amplitude characteristic in the assigned channel cross-section. The same can be stated in relation to the deflections amplitudes distribution functions $A_{i} (x, ω)$ , being frequency dependent ones. The functions $φ_{i} (x, ω),$ $φ_{p} (x, ω)$ are frequency dependent ones of the plates deflections phase shifts distribution and the pressure phase shift along the channel, correspondingly.

The investigation of the above mentioned functions behavior, depending on oscillations frequency, makes it possible to study dynamic processes in the channel under consideration. The obtained expressions for channel walls deflections analysis allows to state that the elastic coefficient of Winkler foundation in a static state causes deflection reduction of the first plate, deflections amplitude dynamics reducing in both plates in a dynamic state. Thus, the paper results can be used for calculation and analysis hydroelastic oscillations of channel walls on elastic foundation and for calculation of hydraulic dampers, pumps elements, hydrodrives, lubrication, cooling and fuel supply systems.

References

Gorshkov A. G., Morozov V. I., Ponomarev A. T., Shklyarchuk F. N. Aerouprugost konstruktsii (Aerogidroelasticity of designs), Fizmathlit, Moscow, 2000, (in Russian).

Search CrossRef
Haddara M. R., Cao S. A study of the dynamic response of submerged rectangular flat plates. Marine Structures, Vol. 9, Issue 10, 1996, p. 913-933.

Search CrossRef
Avramov K. V., Strel’nikova E. A. Chaotic oscillations of plates interacting on both sides with a fluid flow. International Applied Mechanics, Vol. 50, Issue 3, 2014, p. 303-309.

Search CrossRef
Amabili M. Vibrations of circular plates resting on a sloshing liquid: solution of the fully coupled problem. Journal of Sound and Vibration, Vol. 245, Issue 2, 2001, p. 261-283.

Search CrossRef
Askari E., Jeong K.-H., Amabili M. Hydroelastic vibration of circular plates immersed in a liquid-filled container with free surface. Journal of Sound and Vibration, Vol. 332, Issue 12, 2013, p. 3064-3085.

Search CrossRef
Indeitsev D. A., Polypanov I. S., Sokolov S. K. Calculation of cavitation life-time of ship engine liner. Problemy Mashinostraeniya i Nadezhnos’ti Mashin, Vol. 4, 1994, p. 59-64.

Search CrossRef
Akcabay D. T., Young Y. L. Hydroelastic response and energy harvesting potential of flexible piezoelectric beams in viscous flow. Physics of Fluids, Vol. 24, Issue 5, 2012.

Search CrossRef
Faria Cassio T., Inman Daniel J. Modeling energy transport in a cantilevered Euler-Bernoulli beam actively vibrating in Newtonian fluid. Mechanical Systems and Signal Processing, Vol. 45, 2014, p. 317-329.

Search CrossRef
Önsay T. Effects of layer thickness on the vibration response of a plate-fluid layer system. Journal of Sound and Vibration, Vol. 163, 1993, p. 231-259.

Search CrossRef
Mogilevich L. I., Popov V. S., Popova A. A. Dynamics of interaction of elastic elements of a vibrating machine with the compressed liquid layer lying between them. Journal of Machinery Manufacture and Reliability, Vol. 39, Issue 4, 2010, p. 322-331.

Search CrossRef
Mogilevich L. I., Popov V. S. Investigation of the interaction between a viscous incompressible fluid layer and walls of a channel formed by coaxial vibrating discs. Fluid Dynamics, Vol. 46, Issue 3, 2011, p. 375-388.

Search CrossRef
Ageev R. V., Mogilevich L. I., Popov V. S. Vibrations of the walls of a slot channel with a viscous fluid formed by three-layer and solid disks. Journal of Machinery Manufacture and Reliability, Vol. 43, Issue 1, 2014, p. 1-8.

Search CrossRef
Ageev R. V., Kuznetsova E. L., Kulikov N. I., Mogilevich L. I., Popov V. S. Mathematical model of movement of a pulsing layer of viscous liquid in the channel with an elastic wall. PNRPU Mechanics Bulletin, Vol. 3, 2014, p. 17-35.

Search CrossRef
Mogilevich L. I. Dynamics of interaction between a squeezed layer of a viscous incompressible fluid and an elastic three-layer plate. Mechanics of Solids, Vol. 43, Issue 5, 2008, p. 785-792.

Search CrossRef
Grushenkova E. D., Mogilevich L. I., Popov V. S., Rabinsky L. N., Kuznetsova E. L. Mathematical model of three-layer plate interaction with viscous incompressible liquid layer under foundation vibration. Applied Mathematical Sciences, Vol. 9, Issue 2015, 112, p. 5551-5559.

Search CrossRef
Alekseev V. V., Indeitsev D. A., Mochalova Yu A. Resonant oscillations of an elastic membrane on the bottom of a tank containing a heavy liquid. Technical Physics, The Russian Journal of Applied Physics, Vol. 44, Issue 8, 1999, p. 903-907.

Search CrossRef
Panovko Y. G., Gubanova I. I. Stability and Oscillations of Elastic Systems. Consultants Bureau Enterprises, Inc., New York, N. Y., 1965.

Search CrossRef
Loitsyanskii L. G. Mechanics of Liquids and Gases. Pergamon Press, Oxford, 1966.

Search CrossRef

About this article

Received

29 May 2016

Accepted

24 August 2016

Published

07 October 2016

SUBJECTS

Flow induced structural vibrations

Keywords

hydroelastic oscillations

viscous liquid

plate

vibrations

Winkler foundation

Acknowledgements

The research is made under the financial support of the Russian Foundation for Basic Research (RFFI) Grant 15-01-01604-a.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.