Abstract
We establish an analytical model to investigate the surface effects on the vibration and instability of fluid-conveying nanotubes embedded in visco-elastic medium. Based on nonlocal elastic theory and Euler-Bernoulli beam theory, the vibration equation of fluid-conveying nanotubes is established with considering three typical boundary conditions. The effects of both inner and outer surface layers on the nanotubes are taken into consideration and the Kelvin-Voigt model is introduced. The results show that the boundary conditions of system, the damping and elastic coefficient of the surrounding medium, thickness of nanotubes and aspect ratios have significant effects on the dynamic behaviors of the nanotubes. The damping parameter of the visco-elastic foundation causes an obvious reduction of the critical flow velocity. For smaller tube thickness, larger aspect ratio or higher elastic parameter of surrounding foundation, the stability of the nanotubes may be greatly enhanced. This article might be helpful for the design and improvement of nanotubes for fluid-conveying applications embedded in elastic medium in nanoelectromechanical systems and microelectromechanical systems.
1. Introduction
For the wide applications of nanotubes/nanopipes in nanoelectromechanical systems (NEMS) and microelectromechanical systems (MEMS), many attempts have been made to study their properties [1, 2]. Due to the hollow cylindrical geometry structure of nanotubes, they are expected to be used as nanofluidic devices and systems, with potential application in fluid filtration devices, biomimetic selective transport of ions, targeted drug delivery devices and so on [3-5].
As a small scale fluid-structure interaction system, the fluid-conveying nanotubes show higher sensitivity to the vibration characteristics. The research of flow-induced vibration and instability is of fundamental significance. In the past two decades, the literature on this topic has been constantly expanding. Many researchers have done much work in this area [6-12]. The systems they studied range from straight to curved configurations of nanotubes with either single wall or multi walled, linear and nonlinear vibration [13-16].
In classical continuum mechanics, the surface energy is usually small and negligible. But when materials and structures shrink to nanometers, it plays a critical role in their static or dynamical behavior due to the high specific surface area of nanomaterials [17]. He and Lilley [18] studied the effects of surface tension on the static bending of nanowires. Farshi et al. [19] researched the vibration of nanotubes with consideration of surface effects utilizing Timoshenko beam model. Gheshlaghi and Hasheminejad [20] investigated the surface effects on the nonlinear vibration of nanobeams based on the Euler-Bernoulli beam theory including the von Kármán geometric nonlinearity.
The vibration and buckling instability of fluid-conveying nanotubes by accounting for surface layers were analyzed by Wang [21], who found that the natural frequencies and critical flow velocity are strongly related to the surface effect. With the increasing ratio of surface layer to volume (nanotube wall) at the nanoscale, the vibration characteristics of nanotubes conveying fluid were shown to exhibit distinct size dependences. Furthermore, the surface effect on the buckling and post-buckling behavior of a nanobeam with supported ends containing flowing fluid is investigated using a nonliner model [22].
In this paper, an analytical model is established to invesitigate the surface effect on the vibration and instability of fluid-conveying nanotubes embedded in viso-elastic medium by nonlocal Euler-bernoulli beam model. It will be shown that the current model will be helpful for designing the nanotubes for fluid-conveying applications embedded in visco-elastic medium in NEMS and MEMS.
2. Fundamental equations
The circular nanotube embedded in visco-elastic medium is modeled as a straight and slender nanobeam with length , as shown in Fig. 1. From reference [12] we get the vibration equation of fluid-conveying nanotube embedded in visco-elastic medium based on nonlocal Euler-Bernoulli beam theory as follow:
where is the transverse displacements of the nanotube along the -axis at time , is the flexural rigidity of the tube without surface layers, and are the mass of nanotube and the mass of the fluid per unit length respectively, is the flow velocity of the internal fluid. and are the elastic stiffness and damping coefficient of the surrounding visco-elastic medium based on the Kelvin-Voigt model, respectively. represents the effect of nonlocal elasticity, and when it equals to zero, the equation reduces to classical condition.
Fig. 1Schematic diagram of a) a fluid-conveying nanotube embedded in visco-elastic medium; b) the circular cross section with surface layers
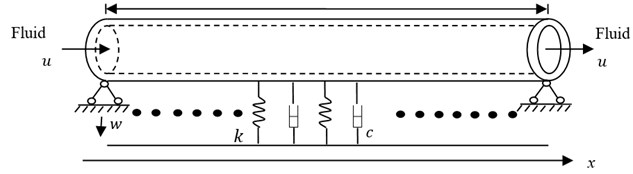
a)
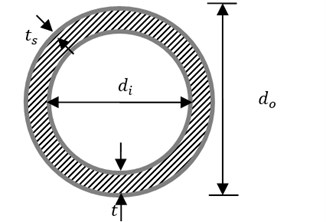
b)
Surface effects on the mechanical behaviour of nanomaterials can be examined by considering surface energy and surface residual stresses. The surface energy mainly acts as an increased effect on bending rigidity, the effect with surface residual stress acts as distributed transverse loads and can be calculated by Laplace-Young equations [19]. The additional flexural rigidity of nanotube due to the inner and outer surface layers may be written as [19]:
where and are Young’s modulus and thickness of both surface layers, and are the inner and outer diameters of the nanotube, respectively, as shown in Fig. 1(b). The distributed transverse loads induced by the surface residual stress is and the constant is given by:
where is the residual surface tension.
Considering the influence of two surface layers, the equation of motion of the fluid-conveying nanotube embedded in visco-elastic medium can be written as:
Three typically boundary conditions are considered:
(i) A beam simply supported at both ends, i.e. pinned-pinned condition (P-P):
(ii) A beam clamped at both ends, i.e. clamped-clamped condition (C-C):
(iii) A beam clamped at one end and simply supported at the other end, i.e. clamped-pinned condition (C-P):
For simplicity, introducing dimensionless variables as follows:
Eq. (4) can be written in the dimensionless form:
The boundary conditions are converted to the following:
P-P condition:
C-C condition:
C-P condition:
3. Numerical results
We use the Differential Quadrature Method (DQM) to obtain the solutions of Eqs. (9)-(12). For calculations convenience, the nanotube with circular cross-section area is assumed to be made of anodic alumina with crystallographic of [1 1 1] direction. The parameters may be chosen as follows: 70 GPa, 2700 kg/m3 (mass density of the tube), 5.1882 N/m, 0.9108 N/m [19], 1000 kg/m3 (mass density of the internal water), 1 nm, 1.02×10-4 Pa·S, 20 nm. According to the work by Farshi et al. [19], for nanostructures made of anodic alumina material, surface effect maybe the most important factor associated with the size-dependent properties.
Fig. 2 shows the variation of the first natural frequency with respect to the dimensionless flow velocity, for different boundary conditions and thicknesses () of the nanotube. It can be seen that the natural frequency decreases as the flow velocity increases and the nanotube buckles when the flow velocity increase to a critical value. The results demonstrate that as the bending stiffness of the nanotube rises from P-P to C-C, the corresponding natural frequencies and the dimensionless critical flow velocities increase. It can be observed that surface effects generally increase the natural frequency and critical flow velocity comparing to the counterpart without surface effects especially for smaller tube thickness. The thickness has a negative influence on the natural frequency, i.e., the smaller the thickness, the larger the natural frequency.
Fig. 2Natural frequency as functions of dimensionless flow velocity
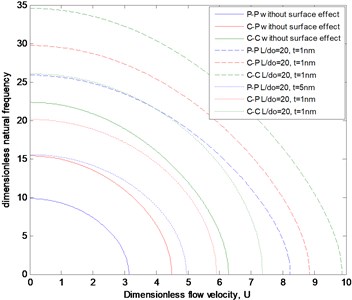
Fig. 3Critical flow velocity as functions of tube thickness
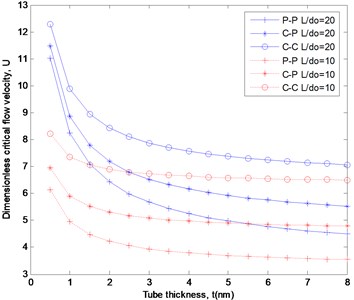
Fig. 3 shows the surface effects on the critical flow velocity, for various values of tube thickness and different aspect ratios. It is found that the influence of surface layers on the critical flow velocity is significant, especially for nanotubes with smaller tube thickness or larger aspect ratio. For example, in the case of 20 and 0.5 nm, the critical flow velocity predicted with surface layers is about 3.51 times than that predicted without surface layers, which implies that the surface layers enhance the stability of fluid-conveying nanotubes. The influence of surface layers on critical flow velocity decreases as the tube thickness increases.
Fig. 4Critical flow velocity as functions of dimensionless damping coefficient
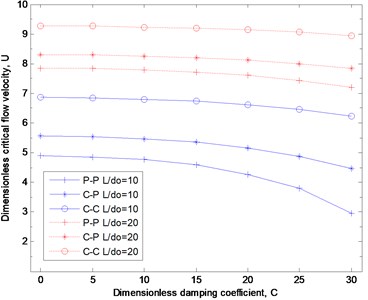
Fig. 5Critical flow velocity as functions of dimensionless Winkler parameter
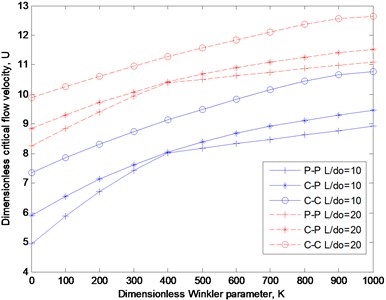
The effect of the surrounding visco-elastic medium on the critical flow velocity of nanotube is shown in Fig. 4 and Fig. 5 for different aspect ratios. The dimensionless parameters and are used to demonstrate the effects of the visco-elastic behavior of the foundation. It can be concluded from Figs. 4 and 5 that the critical velocity is significantly influenced by the damping and elastic parameter especially for smaller aspect ratio. By increasing the dimensionless damping coefficient or decreasing the dimensionless elastic parameter , the dimensionless critical flow velocity decreases. This implies that a higher damping property dissipates the vibrational energy quickly and the resonant frequency vanishes at a lower flow velocity, and the elastic parameter enhance the stability of the fluid-conveying nanotube.
4. Conclusions
In summary, an analytical model is developed to investigate the surface effects on the vibration and stability analysis of fluid-conveying nanotubes embedded in visco-elastic medium. The results show that the damping and elastic coefficient of medium, thickness of nanotubes and aspect ratios have significant effects on the dynamic behaviors of the nanotubes. This article might be helpful for the design and improvement of nanotubes for fluid-conveying applications embedded in elastic medium in NEMS and MEMS.
References
-
Gibson R. F., Ayorinde E. O., Wen Y. F. Vibrations of carbon nanotubes and their composites: a review. Composites Science and Technology, Vol. 67, 2007, p. 1-28.
-
Li C., Thostenson E. T., Chou, T.-W. Sensors and actuators based on carbon nanotubes and their composites: a review. Composites Science and Technology, Vol. 68, Issue 6, 2008, p. 1227-1249.
-
Gadd G. E., Blackford M., Moricca S., Webb N., Evans P. J., et al. The world’s smallest gas cylinder. Science, Vol. 277, 1997, p. 933-936.
-
Yang Z., Zhang Y., Yang Y., Sun L., Han D., et al. Pharmacological and toxicological target organelles and safe use of single-walled carbon nanotubes as drug carriers in treating Alzheimer disease. Nanomedicine-Nanotechnology Biology and Medicne, Vol. 6, 2010, p. 427-441.
-
Gao Y. H., Bando Y. Nanotechnology: Carbon nanothermometer containing gallium. Nature, Vol. 415, 2002, p. 599-599.
-
Yoon J., Ru C. Q., Mioduchowski A. Vibration and instability of carbon nanotubes conveying fluid. Composites Science and Technology, Vol. 65, 2005, p. 1326-1336.
-
Yoon J., Ru C. Q., Mioduchowski, A. Flow-induced flutter instability of cantilever carbon nanotubes. International Journal of Solids and Structures, Vol. 43, 2006, p. 3337-3349.
-
Chang W. J., Lee H. L. Free vibration of a single-walled carbon nanotube containing a fluid flow using the Timoshenko beam model. Physical Letters A, Vol. 373, 2009, p. 982-985.
-
Khosravian N., Rafii-Tabar H. Computational modeling of the flow of viscous fluids in carbon nanotubes. Journal of Physics D: Applied physics, Vol. 40, 2007, p. 7046-7052.
-
Yan Y., He X. Q., Zhang L. X., Wang Q. Flow-induced instability of double-walled carbon nanotubes based on an elastic shell model. Journal of Applied Physics, Vol. 102, 2007, p. 044307.
-
Wang L. Dynamical behaviors of double-walled carbon nanotubes conveying fluid accounting for the role of small length scale. Computational Materials Science, Vol. 45, 2009, p. 584-588.
-
Zhen Y. X., Fang, B. Thermal-mechanical and nonlocal elastic vibration of single-walled carbon nanotubes conveying fluid. Computational Materials Science, Vol. 49, 2010, p. 276-282.
-
Xia W., Wang L. Vibration characteristics of fluid-conveying carbon nanotubes with curved longitudinal shape. Computational Materials Science, Vol. 49, 2010, p. 99-103.
-
Ghavanloo E., Rafiei M., Daneshmand F. In-plane vibration analysis of curved carbon nanotubes conveying fluid embedded in viscoelastic medium. Physics Letters A, Vol. 375, 2011, p. 1994-1999.
-
Wang Y. Z., Li F. M. Nonlinear free vibration of nanotube with small scale effects embedded in viscous matrix. Mechanics Research Communications, Vol. 60, 2014, p. 45-51.
-
Zhen Y. X., Fang B. Nonlinear vibration of fluid-conveying single-walled carbon nanotubes under harmonic excitation. International Journal of Non-Linear Mechanics, Vol. 76, 2015, p. 48-55.
-
She H., Wang B. A geometrically nonlinear finite element model of nanomaterials with consideration of surface effects. Finite Elements in Analysis and Design, Vol. 45, 2009, p. 463-467.
-
He J., Lilley C. M. Surface effect on the elastic behavior of static bending nanowires. Nano Letters, Vol. 8, Issue 7, 2008, p. 1798-1802.
-
Farshi B., Assadi A., Alinia-ziazi A. Frequency analysis of nanotubes with consideration of surface effects. Applied Physics Letters, Vol. 96, 2010, p. 093105.
-
Gheshlaghi B., Hasheminejad S. M. Surface effects on nonlinear free vibration of nanobeams. Composites: Part B, Vol. 42, 2011, p. 934-937.
-
Wang L. Vibration analysis of fluid-conveying nanotubes with consideration of surface effects. Physica E, Vol. 43, 2010, p. 437-439.
-
Wang L. Surface effect on buckling configuration of nanobeams containing internal flowing fluid: A nonlinear analysis. Physica E, Vol. 44, 2012, p. 808-812.
About this article
This work is supported by National Natural Science Foundation of China under Grant No. 11402087 and The Fundamental Research Funds for the Central Universities (No. 2016MS64).
