Abstract
The human head-neck is the most complex structure in the human body and its behavior under vibration remain poorly understood. Therefore, a comprehensive theoretical or experimental analysis is needed. This study is mainly based on an available finite element human head-neck complex and concentrates on its modal and dynamic responses. Resonance frequencies and responses of the human head-neck complex’s finite element model in impact simulations have been analyzed. These dynamic responses show a very good agreement with the previous studies. The fundamental frequency of modal analysis of finite element model is 35.25 Hz which is reasonably close to existing literatures. However, our modal dynamic analysis of an elaborated human head-neck complex introduces supplementary dynamic responses like nasal sideward cartilages’ “flipping” modes and the mandible’s “mastication” modes. Modal validation is performed which indicates a requirement for elaborated modeling to make out all the extra resonance frequencies. Moreover, the influence of damping factor on biomechanical response or natural frequencies is also investigated. It can be found that damping factor has got an inverse proportionality between damping factor effect on natural frequency and that on biomechanical responses. This demonstrates the significance of identification of the suitable damping factor evaluating biomechanical response in modal dynamic analysis and validation.
1. Introduction
When exposed to shock and vibration either in acoustic domain or keeping in touch with vibratory continuous constructions. The human head-neck complex responds under vibration with resonant frequencies, its vibration intensity relies on its own detailed structure [1]. Finding out the knowledge of how or why it resonates will result in an overall apprehension of human biomechanics. This may help in evolution of “a new medical instrument for brain diseases’ early diagnosis” [2] or a protective device in both military circumstances and civilian.
Earlier studies on the human head-neck vibration were primarily focused on experimental tests that involved cadavers, volunteer and animals. Bekesy [3] looked into a cadaver skull’s vibration response in acoustic domain and found the fundamental natural spectrum of the human skull was 1800 Hz. Franke [1] executed the experimental modal study by a hollow skull and the equivalent skull which was full of gelatin, discovered that the fundamental natural frequencies individually were 500 Hz and 800 Hz. Both Gurdjian et al. [4] and Kitazaki et al. [5] discovered “the natural spectrum of a human cadaver head-neck in its modal dynamic simulation” was just about 300 Hz. In comparison with the fact that Deng and Goldsmith [6] applied “an electromagnetic shaker in the experiments of a novel unembalmed cadaver brain” and concluded that the natural spectrums were 166 Hz and 820 Hz. An empirical study was conducted by khalil et al. [7] on “two cadaver’s heads (one female and one male) adopting an impact hammer”. The individual principle spectrums that were found were 1641 Hz and 1385 Hz. Hakansson et al. [8] applied “skin that penetrates titanium implants on patients’ temporal that is asserted” that the principal free resonance spectrum was just approximately 972 Hz. By comparison, empirical tests result on living human topics indicated 300 Hz the resonant frequency that was organized from several Hz [1, 5, 9-11]. In spite of the majority of important results supplied by empirical information, these examinations cause subjects in ethics and put forward a large number of research concerns like circumscribed biasness as well as flexibility in experimental information because of non-standardized experimental procedures and scarce topics. Furthermore, results from experimentations may differ from the individual topic and therefore may illustrate a scarcity of reliability and reproducibility.
In other words, a cost-efficient option to experimental approaches is provided by mathematical calculations using finite element method, which bring out a possibility for assessments exceed the experimental moral limits and would assist in more effective equipment’s development. Nickell and Marcal [12] had executed mathematical calculations utilizing a simple three-dimensional finite element skull model and concluded the cardinal brain spectrums for occipital and frontal supports respectively were 68 Hz and 86 Hz. Comparable finite element models afterwards evolved by Thompson and Ward [13] computed brain’s fundamental frequency to respectively be 43 Hz and 23 Hz. Ruan et al. [14] built “a two-dimensional finite element head-neck model which included brain membranes utilizing a coronal segment of human being head” and discovered that the fundamental resonance spectrum dropped between 49 Hz and 72 Hz. “two two-dimensional midsaggital head-neck models (one with brain; one with a hollow skull)” was built by Chu et al. [15] and found the extra brain reduced the cardinal spectrum from 286 Hz to 119 Hz. The head’s models were presented by these studies merely until lately, while Charalambopoulos et al. [2] built an analytic detailed head-neck complex and discovered that the neck brought in extra spectrum domain with the resonance frequency of 595 Hz. Afterwards, Meyer et al. [16]’s finite element simulations that used a head-neck system illustrated that the head-neck model’s fundamental frequency was 3.01 Hz. Recently, Baroudi et al. [17] executed a three-dimensional modal dynamic analysis of a simplified cylindrical skull-brain-CSF model utilizing both analytic and finite element approaches and discovered the principle spectrum for that is 26.66 Hz.
A number of perceptions had been offered by these previous finite element studies in the human head-neck’s modal and dynamic responses. However, numerous simplifications and estimations had been made in the head-neck’s geometry. In the present work, an elaborated human head-neck’s finite element model has been built and its modal dynamic features have been discussed, the model embraces detailed facial and brain tissues. Besides, the calculated dynamic characteristics according to shape and natural spectrum are in comparison with those reported documents, which is different from mainly former investigations comparing the first natural spectrum and disregarded modal validation. Furthermore, damping factor’s influence on dynamic properties is likewise investigated, a few damping factors are introduced in the matrix eigenvalue and eigenvector analyses, differ from most former finite element analysis using the extraction approach of fundamental frequency.
2. Modal analysis of the finite element model
2.1. Governing equation and finite element method
A modal analysis for the finite element head-neck model is conducted. It is reminded that carrying out a mathematical modal analysis of the head-neck system depends fundamentally on resolving the separate equation for free vibration, which can be expressed as follows:
where , and are mass matrix, the displacement vector and rigidity matrix.
The displacement vector is a function of space and time which can be written in the form:
where is a vector of constants providing the mode’s eigenform, whilst is a function illustrating the mode amplitude’s sinusoidal temporal tendency.
The following equation is fulfilled by the temporal part:
and has got the following solution:
The following equation is fulfilled by the spatial part:
The system solution consequently depends on finding the eigenvectors in a way corresponding to the eigenvalues , where symbolizes the natural frequencies. The spacial matrix, or the eigenfrequency matrix, is defined using the following quotient:
where is the shape vector being connected with the eigenpulse, symbolizes the modal deformation in a similar way called mode shape.
2.2. Development of the 3D finite element head-neck model (FEHM)
The FEHM was developed by means of the semi-automatic method of different tissue types’ segmentation in the human head-neck complex, followed by the problem domain’s discretization into number of finite elements. In the meantime, relying on the problem’s nature, material properties need to be assigned to every finite element and boundary conditions need to be applied to the finite element model ahead of its applications in numerical simulations.
In the present work, the human skull’s geometric information is acquired from 600 axial pictures with resolution of 512 by 512 pixels, from a series of a 50th percentile volunteer’s CT and MRI scan information. A global threshold scope of Hounsfield units is selected to segment the skull’s denser bony structure from the soft tissues. Region that grows algorithm is used to filter the floating pixels or “noise” which do not join up to the skull bones when cavity fill techniques are adopted to close the small cavities in the body. The segmented skull’s connectivity is further upgraded by manual in both 3D and 2D. All the internal details, which were frequently disregarded in earlier studies, such as frontal, maxillary sinuses and sphenoidal as well as the inferior, senior and middle turbinates, are in a similar way modeled.
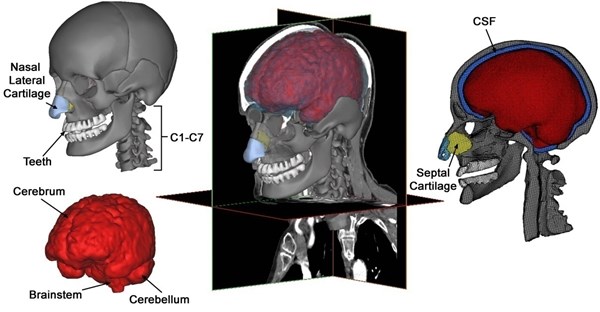
Brain segmentation is crucial for modeling head injury models’ precise brain geometry. The tools for automatic segmentation of soft tissues from CT imaging are not extremely accurate and difficult for brain tissues, although these tools are available utilizing default option threshold scope for “muscle tissue”. Consequently, MRI information of another healthy patient likewise acquired from the scanned database, is mapped and scaled to CT scan information for brain segmentation. The brain is initially segmented into just the cerebellum and cerebrum without gray and white matters’ further differentiation. Afterwards, so as to simulate the strain distribution and stress in a better way, separated representations of the ventricular structure as well as gray and white gray matters are implemented. Ventricular structures as well as the gray and white matters of the skull-brain tissues can be segmented from MRI pictures, utilizing the segmentation approach that is built by Dale et al. [18] and afterwards by Fischl et al. [19] with less manual edition. The model is composed of the cranial skull with elaborate facial bone attributes, cervical vertebrae, teeth, nasal lateral cartilages, nasal septal cartilage; brain components such as cerebellum and cerebrum and the cerebrospinal fluid separating the brain and the skull (Fig. 1).
Though meshes in normal size are most desired in modal and dynamic responses analysis, this is not potential in our numerical simulation of such complicated human head-neck model. Mesh refinement is needed by areas such as those of special interest and of elaborated attributes. An adaptive semi-automatic meshing technique is then utilized to optimize between element quality and computation efficiency. Further mesh reparation is executed to get ready for 3D mesh generation. In spite of the cavity-dominant skull’s complex geometry, it is possible to hexahedrally mesh model utilizing isomorphism technique [20], bringing about a model of 403176 hexahedral elements and 483711 nodes.
Fig. 1Various components of a subject-specific model of the human head-neck segmented from CT and MRI data
2.3. Validation of the 3D finite element head-neck model
The former section introduces details in the description and development of FEHMs. Proper validations in the viewpoint of the models’ intended uses, however, ought to be executed before their dynamic applications. A numerical model’s experimental validation, ahead of its applications, is significant and required in deciding the degrees to which a model accurately predicts the physical phenomena of the real-world. Only when this is accomplished, it does represent a powerful tool with which to correlate the biomechanical parameters that are involved in the head injury. Before analyzing the numerical results obtained with the finite element method, the reliability of the numerical results themselves could be guaranteed.
The finite element model of the human head-neck complex was validated against intracranial pressure data of Nahum et al. [21]’s cadaver experiments, with some that was validated against extra pressure history information for Trosseille et al. [22]’s long duration impact. Further, the FEHM was validated against relative displacement information between brain and skull supplied by Hardy et al. [23]. These validations involve impact force, the intracranial pressure and intracranial acceleration response. The FEHM demonstrated good agreement with post mortem human subjects’ information according to the injury prediction and biomechanical response in validation test. Apart from very good estimations in terms of injuries and biomechanical response, the model illustrated stability at severe loading circumstances. Overall results that were acquired in the validation showed improved biofidelity that was in relation to former finite element models.
2.4. Frequency spectrum of the human head-neck complex
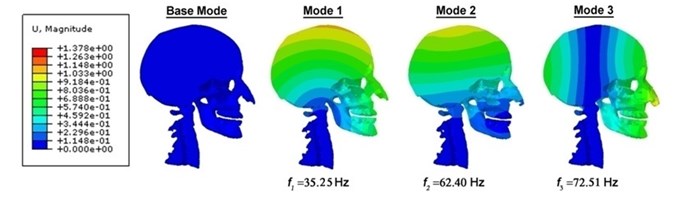
By performing modal dynamic analyses of three-dimensional mathematical model of the head-neck complex which is introduced in the former part with 25 frequency spectrums in Abaqus, related modal and an inexplicit finite element code figures are acquired in the frequency domain between 35 Hz and 360 Hz (Table 1). Resonant frequencies which were computed under the condition of the damped and undamped free vibration are listed in Table 1, and with individual fundamental natural frequencies of 35.25 Hz, 34.50 Hz, 34.23 Hz and 33.38 Hz. Additionally, there is a fluctuation within a narrow range in the inherent frequencies under the damped vibration circumstances and undamped ones, which are given in Table 1. In the 25 modal shapes, the head-neck complex’s five diverse, distinguishable mode shapes are demonstrated: a posterior-anterior flexion-extension mode about the neck of 35.25 Hz, a sideward inflexion mode of 62.40 Hz, a co-axial rotational mode of 72.51 Hz, an S-shaped posterior-anterior mode of 221.59 Hz and eventually a perpendicular translational mode of 254.04 Hz. The nasal sideward cartilages’ transverse flexion and the horizontal movement of the “mastication” or “mandible” mode which predominate after the head-neck complex’s fundamental modes in the twenty-five modals are likewise discovered. The modal shapes under the undamped vibration circumstances are the same as that under the damped ones, aside from the difference in biomechanical properties like displacement, Mises stresses of skull as well as intracranial pressure (Table 2). Table 2 also suggests the positions of vertex intracranial pressure and vertex Mises stresses of skull that is corresponding to each mode.
Table 1Modal and dynamic responses of the finite element head-neck model
Mode No. | Without damping | With damping | Mode shape description | Resonated location | ||
0.1 | 0.2 | 0.4 | ||||
Eigenfrequencies (Hz) | Eigenfrequencies (Hz) | Eigenfrequencies (Hz) | Eigenfrequencies (Hz) | |||
1 | 35.25 | 34.50 | 34.23 | 33.38 | Posterior-anterior flexion-extension of the head mode | Whole head |
2 | 62.40 | 57.72 | 57.59 | 57.07 | Sideward inflexion of the head | Whole head |
3 | 72.51 | 74.56 | 74.43 | 73.91 | Co-axial rotational of the head | Whole head |
4 | 131.35 | 121.00 | 120.78 | 119.89 | Vertical shutting of the jaws | Mandible |
5 | 221.59 | 221.06 | 220.55 | 218.50 | The head-neck’s S-shaped posterior-anterior; Vertical opening of the jaws | Brain, Mandible, Sideward cartilage, Teeth |
6 | 229.64 | 227.51 | 226.93 | 224.62 | The nasal sideward cartilages’ sideward inflexion | Sideward cartilage |
7 | 237.06 | 237.95 | 237.30 | 234.67 | Sideward motion of mandible | Brain, Sideward cartilage |
8 | 254.04 | 253.80 | 253.08 | 250.19 | Perpendicular translation of the head; The nasal sideward cartilages’ sideward inflexion | Brain, Sideward cartilage, Septal cartilage |
9 | 256.47 | 257.89 | 257.14 | 254.13 | Axial rotational of the head; Sideward inflexion of the nasal sideward cartilages | Brain, Sideward cartilage, Septal cartilage |
10 | 270.16 | 270.13 | 269.31 | 265.98 | Sideward inflexion of the head; Sideward motion of mandible | Brain, Septal cartilage |
11 | 273.31 | 273.25 | 272.55 | 269.76 | Sideward inflexion of the head and mandible; Flipping of nasal septal cartilage | Septal cartilage |
12 | 277.10 | 277.42 | 276.53 | 272.94 | The head-neck’s S-shaped anterior-posterior retraction; Vertical opening of the jaws | Brain, Sideward cartilage, Septal cartilage |
13 | 283.20 | 283.44 | 282.45 | 278.45 | Vertical shutting of the jaws | Brain, Sideward cartilage, Septal cartilage |
14 | 295.85 | 295.54 | 294.49 | 290.25 | Sideward motion of mandible | Brain, Mandible, Sideward cartilage, Septal cartilage |
15 | 299.86 | 298.60 | 297.52 | 293.15 | Sideward inflexion of head; Sideward motion of mandible | Brain, Mandible, Sideward cartilage |
16 | 300.97 | 297.80 | 296.70 | 292.27 | Sideward inflexion of head; Sideward motion of mandible | Brain, Mandible, Septal cartilage |
17 | 316.08 | 315.84 | 314.62 | 309.68 | Sideward motion of mandible | Brain, Mandible |
18 | 317.74 | 317.61 | 316.38 | 311.38 | Vertical translation of the head | Brain |
19 | 322.55 | 321.54 | 320.26 | 315.09 | Sideward inflexion of the head | Brain, Mandible |
20 | 328.78 | 329.16 | 327.80 | 322.31 | Vertical translation of the head; Sideward teeth crunching | Brain, Mandible |
21 | 329.97 | 329.94 | 328.57 | 323.05 | Vertical translation of the head | Brain |
22 | 336.50 | 336.42 | 334.98 | 329.17 | Sideward inflexion of the head | Brain |
23 | 337.68 | 336.88 | 335.43 | 329.58 | Vertical opening of the jaws; Vertical flipping of nasal sideward cartilage tip | Brain, Sideward cartilage |
24 | 351.17 | 350.90 | 349.29 | 342.78 | Sideward motion of the mandible | Brain, Mandible |
25 | 356.39 | 355.91 | 354.25 | 347.51 | Sideward motion of the mandible | Brain |
Table 2Vertex intracranial pressure and vertex skull stress both damped and undamped circumstances
Mode No. | Max intracranial pressure (MPa) | Max skull mises stress (MPa) | ||||
Without damping | With damping ( 0.2) | Location of vertex value | Without damping | With Damping ( 0.2) | Location of vertex value | |
1 | 3.16E-02 | 4.79E-03 | Posterior Cerebellum^ | 4.05E+01 | 2.15E+01 | C2# |
2 | 3.77E-02 | 7.88E-03 | Left Parietal Lobe^ | 9.54E+01 | 3.65E+01 | C2# |
3 | 2.46E-02 | 1.85E-02 | Anterior Right Cerebellum^ | 2.67E+01 | 2.65E+01 | C2 |
4 | 2.27E-03 | 2.50E-03 | Antero-superior Frontal Lobe | 3.20E+01 | 8.38E+00 | Right Mandibular Condyle# |
5 | 6.83E-02 | 5.33E-02 | Anterior Brainstem^ | 1.62E+02 | 1.45E+02 | Occiptal Bone-C1 Interface# |
6 | 6.27E-04 | 4.19E-04 | Posterior Right Temporal Lobe | 3.33E+00 | 1.12E+00 | Sideward Cartilage |
7 | 2.46E-02 | 2.15E-02 | Posterior Right Temporal Lobe | 1.30E+01 | 1.13E+01 | C2 |
8 | 1.27E-01 | 8.65E-02 | Brainstem^ | 1.55E+01 | 6.43E+00 | Occiptal Bone-C1 Interface# |
9 | 7.87E-02 | 7.25E-02 | Posterior Right Temporal Lobe | 2.42E+01 | 2.24E+01 | C2 |
10 | 4.68E-02 | 4.87E-02 | Posterior Left Parietal Lobe | 7.91E+00 | 3.81E+00 | C2 |
11 | 5.24E-05 | 6.85E-05 | Anterior Right Cerebellum | 2.74E+00 | 2.71E+00 | Vomer-Ethmoidal Region |
12 | 5.24E-02 | 5.14E-02 | Posterior Left Temporal Lobe | 3.07E+01 | 2.96E+01 | C2 |
13 | 4.87E-02 | 4.51E-02 | Anterior Brainstem | 7.17E+01 | 4.41E+01 | Right Mandibular Condyle# |
14 | 4.48E-02 | 2.78E-02 | Posterior Left Temporal Lobe^ | 1.22E+02 | 1.10E+02 | Left Mandibular Notch# |
15 | 6.26E-02 | 5.93E-02 | Anterior Right Cerebellum | 1.00E+01 | 6.66E+00 | Left Mandibular Notch |
16 | 1.06E-01 | 9.50E-02 | Anterior Cerebellum^ | 5.70E+01 | 2.62E+01 | Right Mandibular Notch# |
17 | 5.20E-02 | 5.42E-02 | Anterior Brainstem | 3.41E+01 | 1.11E+01 | C2# |
18 | 6.76E-02 | 6.14E-02 | Posterior Right Temporal Lobe^ | 3.72E+00 | 2.26E+00 | Right Mandibular Notch |
19 | 4.71E-02 | 4.46E-02 | Posterior Left Temporal Lobe | 1.64E+01 | 4.25E+00 | Right Mandibular Notch# |
20 | 7.82E-02 | 6.90E-02 | Antero-inferior Frontal Lobe^ | 2.69E+01 | 7.92E+00 | Occiptal Bone-C1 Interface# |
21 | 6.81E-02 | 6.03E-02 | Anterior Right Cerebellum^ | 2.92E+00 | 3.48E+00 | Left Mandibular Notch |
22 | 9.69E-02 | 8.00E-02 | Posterior Cerebellum^ | 7.40E+00 | 6.99E+00 | Occiptal Bone-C1 Interface |
23 | 1.31E-01 | 9.90E-02 | Posterior Occipital Lobe^ | 2.51E+01 | 2.40E+01 | Occiptal Bone-C1 Interface |
24 | 9.62E-02 | 7.10E-02 | Posterior Left Temporal Lobe^ | 1.06E+01 | 7.51E+00 | Left Mandibular Notch |
25 | 9.53E-02 | 9.50E-02 | Postero-Inferior Parietal Lobe | 2.736 | 1.48E+00 | Left Mandibular Notch |
^ Modes with conspicuous distinction in vertex intracranial pressure under damped vibrations and undamped ones # Modes with conspicuous distinction in vertex Mises stress of skull under damped vibrations and undamped ones | ||||||
3. Discussion
As demonstrated contour plots of the displacement for the human head-neck complex (Fig. 2), two fundamental resonance frequencies are 35.25 Hz and 62.40 Hz accompanied by the minimal and maximal displacements on the top of head-neck and head connection individually. These likely agree with the whole head’s axial elongation. The third resonance frequency is 72.51 Hz which gets major displacements in front of human head-neck complex, being similar to the head’s longitudinal elongation. From modal dynamic analysis we can know that the head-neck finite element model is additionally obedient to the back-to-front bending in axial rotation of the first two modes. It is demonstrated in contour plots of the displacement that the whole human head-neck model, involving brain tissues and skull resonate jointly of the three fundamental modes. Then, it is followed by various kinds of brain tissues’ resonance in the human head-neck model; nasal sideward cartilages and mandible resonate at the lower frequency modes whereas the brain tissue resonates at the higher frequency modes. However, an interesting phenomenon to be noticed is that displacement contour’s more loops come into view in the head at the higher natural frequency modes, in all probability displaying the shearing, twisting or torsional vibration modes in the head-neck complex. It may appears diffuse axonal injury (DAI) induced by rotation because “rotational skull-brain relative replacement exists mostly in the higher natural spectrum modes whereas translation-induced traumatic brain injury (TBI) exists in the lower natural spectrum modes” [24].
Fig. 2Contour plots of the displacement for the human head-neck complex, indicating their corresponding frequencies and diverse mode shapes under the undamped vibration circumstances
3.1. Comparison of fundamental frequency
The fundamental natural frequency which has been acquired from modal analysis and compared with those that were found in reported documents is one of the significant dynamic characteristics, Because of the difference in the sections involved, the reported fundamental frequencies, nevertheless, differ widely across literatures; from the few thousands for skull-only studies to the few hundred hertz in studies accounting for the brain.
In the present work, Meyer et al. [16]’s finite element study is selected for the modal responses’ comparison as it is the only study that involves the head-neck system similar to the present finite element head-neck model. In the free vibration circumstance, our computed fundamental frequency is 35.25 Hz when Meyer et al. [16] reported that the fundamental frequency is 3.01 Hz. This discrepancy in the fundamental frequency arises between the two finite element head-neck models, probably owning to the distinction in material properties and the approach in modeling, with the former factor being more likely to result in the discrepancy. With the prioritized focus on the neck injury, the head and all the cervical vertebrae of Meyer et al. [16]’s finite element model were modeled as rigid bodies, with all the individuals’ masses and inertial moment taken into consideration. Only the intervertebral discs were modeled as deformable bodies. Conversely, all the components in our finite element head-neck complex are modeled as deformable bodies with the capability to disperse outside energy by means of deformation. Besides, unlike the rigid head of Meyer et al. [16]’s finite element model, our finite element head model comprises skull, subarachnoid space, brain tissues as well as cartilages. By having the various kinds of different components in the head model, particularly with viscous intracranial content’s lumped mass, it is expected that the fundamental frequency of the multi-components system will be lower than that of a one-component system as extra natural frequencies appear on the one-component system’s frequency spectrum.
In conclusion, our computed fundamental frequency of 35.25 Hz is reasonably close to the reported scope of 20 to 30 Hz in previous studies. Though the present value is higher than the few hertz as reported by Meyer et al. [16] and lower than the analytic head-neck complex’s few hundred hertz, it is still considered to fall within a reasonable range ever since the consensus on this dynamic characteristic stays debatable.
3.2. Effect of damping on resonant frequencies and biomechanical responses
Most former studies revealed that the modal dynamic analysis of the human head-neck complex adopted traditional frequency extraction approach and disregarded the influence of damping factor. As has been noted, a few damping factors are introduced in the matrix eigenvalue and eigenvector analysis. As the value of damping factor extends, it is expected that resonant frequencies will be lower. A considerable fluctuation of natural frequencies is noticed under the damped vibration circumstances and undamped ones. In particular, several brain tissues’ dynamic responses exist at the same time in the lower natural frequencies. Since every single component resonates by itself in the medium modes, these distinguish under damped cases and undamped ones fall down. Nevertheless, with the number of resonance modes grows greatly, the distinguish appears to be expanded by the growth of damping factor, in all probability owning to the complex combination and addition of shearing, bending and torsional modes in the brain tissues.
With regard to the influence of the biomechanical properties such as intracranial pressure (ICP) and Mises stresses of skull, damping factor in a similar way seems to have substantial influence on its significances with special resonance modes, as shown in Table 2. That damping factors are introduced in the matrix eigenvalue and eigenvector analysis has greatly reduced maximal Mises stresses of the skull and the maximal ICP, of up to 74.1 % and 84.8 % individually, in particular modes, as shown in Table 2 and Figs. 3-4. These modes with the maximal deviation in vertex skull stresses and ICP between the damped models and undamped are discovered and displayed in Fig. 3 and Fig. 4. It can be found that vertex ICP changes greatly in the principle few modals while the human head-neck either rotates or flexes. The jaw or mandible opens greatly of the continuous modals such as 14th, 18th, 21st, 22nd or 23rd, therefore making the cranium have a relative movement to the brain. The skull-brain relative motion, as previously, brings about gradient variation of ICP [25]. The existence of damping factor will impede the skull-brain movement and bring the ICP down subsequently. In a similar way we notice that the skull head’s vertex stress deviates greatly where the human neck undergoes the maximal Mises stresses. Owning to the lack of muscle tissues and ligaments the “over-stiff” neck in the head-neck model can bring about much higher vertex Mises stresses of the undamped finite element model. Nevertheless, these modal and dynamic responses are reduced under the damped circumstances as a result of the connection of the stiffness matrix and the damping matrix. Therefore, it is of great significant to identify the suitable damping factor in reckoning modal and dynamic responses. Likewise, it ought to be noticed that this damped influence turns strong while damping factor exceeds the value of 0.2, this implies that greater damping factor will not affect the results of dynamic analyses. As increasing damping factor to the value exceeds 0.2 is discovered to produce magnifying influence on lowering frequencies of higher order modals and eliminating effects in reducing vertex modal dynamic features. Consequently, it comes to a conclusion that there is a reverse proportionality between damping factor effect on resonance frequencies and on biomechanical responses.
Fig. 3Contour plots of biomechanical responses of human finite element head-neck model, indicating their vertex values at special important modes
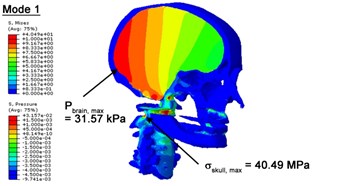
a) 1st mode
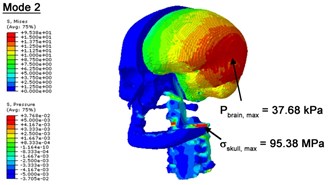
b) 2nd mode
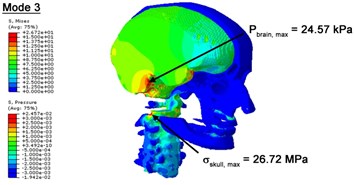
c) 3rd mode
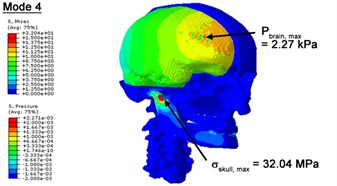
d) 4th mode
3.3. Limitations
The flexibility of the neck, which are highly dependent of the elasticity of the neck ligaments, muscles and intervertebral discs, may not be accurately simulated in present work on account of the lack of the neck ligaments, muscles and intervertebral discs in our model. As a matter of fact, the cervical vertebrae are modeled as deformable bodies, with master-slave restriction between each pair. However, similar to other numerical simulation, the present study made presumption and this accustomed simplification in finite element modeling because its prioritized focal point is to inquire into the effect of damping utilizing complex harmonic eigenvalue modal analysis in which vectors of the computed mode shapes are always not the absolute movement but the arbitrarily relative one. Furthermore, the model provides a reasonable estimation of the mode shapes and natural frequencies, comparable to those in the literature. It, however, shall be emphasized that a more elaborated neck model’s incorporation would be required in the future study for a more comprehensive and precise analyses of neck dynamics.
Fig. 4Contour plots of biomechanical responses of human finite element head-neck model, indicating their vertex values at special important modes
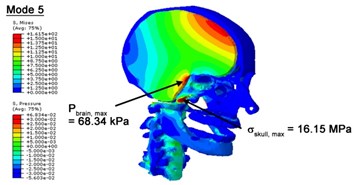
a) 5th mode
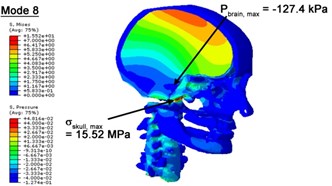
b) 8th mode
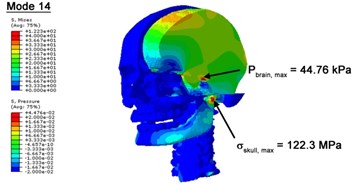
c) 14th mode
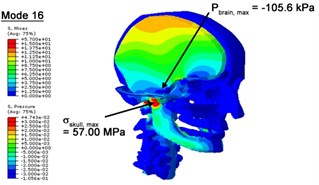
d) 16th mode
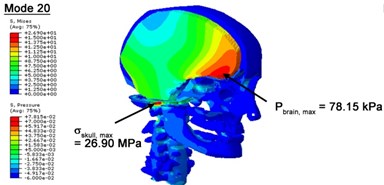
e) 20th mode
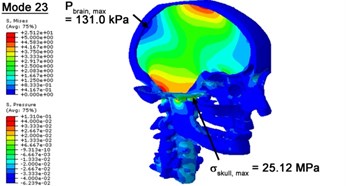
f) 23rd mode
4. Conclusions
1) The modal and dynamic responses, according to mode shapes and frequency spectrum, of the human head-neck complex’s finite element model under vibration circumstances have been calculated. Modal and dynamic responses are discovered to be moderately consistent with previous studies.
2) Supplementary modal responses such as of nasal sideward cartilages’ “flipping” modes and the mandible’s “mastication” modes are introduced. These extra modes may be of great interest to surgeons or clinicians specialized in temporomandibular joint malfunction or rhinoplasty. Modal validation according to modal shapes proposes a requirement for elaborated modeling to identify each individual part’s all additional frequencies.
3) In a similar way, it looks into the influence of damping factor on dynamic characteristics utilizing a matrix analysis for nontraditional complex eigenvalue. The results indicate that damping factor produces a tradeoff influence on decreasing natural resonant spectrum in the higher order modals and on reducing vertex modal dynamic features. Though the finding proposes an optimized estimation of damping factor value of 0.2 for biomechanical responses, it still needs putting emphasis on the deep research in finding out a suitable damping factor.
References
-
Franke K. E. Response of the human skull to mechanical vibrations. Journal of the Acoustical Society of America, Vol. 28, 1956, p. 1277-1284.
-
Charalambopoulos A., Dassios G., Fotiadis D. I., Massalas C. V. Frequency spectrum of the human head-neck system. International Journal of Engineering Science, Vol. 35, Issue 8, 1997, p. 753-768.
-
Bekesy G. V. Vibration of the head in a sound field and its role in hearing by bone conduction. The Journal of the Acoustical Society of America, Vol. 20, Issue 6, 1948, p. 749-760.
-
Gurdjian E. S., Hodgson V. R., Thomas L. M. Studies on mechanical impedance of the human skull: preliminary report. Journal of Biomechanics, Vol. 3, Issue 3, 1970, p. 239-247.
-
Kitazaki S., Griffin M. J. Resonance behaviour of the seated human body and effects of posture. Journal of Biomechanics, Vol. 31, Issue 2, 1998, p. 143-149.
-
Deng Y. C., Goldsmith W. Response of a human head neck upper-torso replica to dynamic loading. 2. Analytical numerical-model. Journal of Biomechanics, Vol. 20, Issue 5, 1987, p. 487-497.
-
Khalil T. B., Viano D. C., Smith D. L. Experimental analysis of the vibrational characteristics of the human skull. Journal of Sound and Vibration, Vol. 63, Issue 3, 1979, p. 351-376.
-
Hakansson B., Brandt A., Carlsson P., Tjellstrom A. Resonance frequencies of the human skull in vivo. Journal of the Acoustical Society of America, Vol. 95, Issue 3, 1994, p. 1474-1481.
-
Willinger R., Bourdet N., Fischer R., Le Gall F. Modal analysis of the human neck in vivo as a criterion for crash test dummy evaluation. Journal of Sound and Vibration, Vol. 287, Issue 3, 2005, p. 405-431.
-
Tse K. M., Tan L. B., Lim S. P., Lee H. P. Conventional and complex modal analyses of a finite element modal of human head and neck. Computer Methods in Biomechanics and Biomedical Engineering, Vol. 18, Issue 9, 2015, p. 961-973.
-
Yang B., Cao L. B., Chen N., Tse K. M., Lee H. P. Dynamic characteristics of finite element (FE) model of the human head-neck. Journal of Vibroengineering, Vol. 16, Issue 7, 2014, p. 3169-3177.
-
Nickell R. E., Marcal P. V. In-vacua modal and dynamic responses of the human skull. Journal of Engineering for Industry, Transactions of the American Society of Mechanical Engineers (ASME) Transaction, Vol. 3, 1974, p. 490-494.
-
Ward C. C., Thompson R. B. The development of a detailed finite element brain model. Proceedings of 19th Stapp Car Crash Conference, New York, USA, SAE Paper 751163, 1975, p. 641-674.
-
Ruan J. S., Khalil T., King A. I. Human head dynamic response to side impact by finite element modeling. Journal of Biomechanical Engineering, Vol. 113, Issue 7, 2014, p. 276-283.
-
Chu C. S., Lin M. S., Huang H. M., Lee M. C. Finite element analysis of cerebral contusion. Journal of Biomechanics, Vol. 27, Issue 7, 1994, p. 187-194.
-
Meyer F., Bourdet N., Willinger R., Legall F., Deck C. Finite element modelling of the human head-neck: modal analysis and validation in the frequency domain. International Journal of Crashworthiness, Vol. 9, Issue 5, 2004, p. 535-545.
-
Baroudi A. E., Razafimahery F., Rakotomanana-Ravelonarivo L. Three-dimensional modal analysis of an idealized human head including fluid–structure interaction effects. Acta Mechanica, Vol. 223, Issue 9, 2012, p. 1899-1915.
-
Dale A. M., Fischl B., Sereno M. I. Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage, Vol. 9, Issue 2, 1999, p. 179-194.
-
Fischl B., Salat D. H., Busa E., Albert M., Dieterich M., et al. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron, Vol. 33, Issue 3, 2002, p. 341-355.
-
Schneiders R. Automatic generation of hexahedral finite element meshes. Proceedings of 4th International Meshing Roundtable, Sandia National Laboratories, 1995, p. 103-114.
-
Nahum A., Smith R., Ward C. Intracranial pressure dynamics during head impact. Proceedings of the 21st Stapp Car Crash Conference, Warrendale, PA, 1977, p. 339-366.
-
Trosseille X., Tarriere C., Lavaste F., Guillon F., Domont A. Development of a FEM of the human head according to a specific test protocol. Proceeding of 36th Stapp Car Crash Conference, Seattle, SAE International Society of Automotive Engineers, 1992, p. 235-253.
-
Hardy W. N., Mason M. J., Foster C. D., Shah C. S., Kopacz J. M., et al. A study of the response of the human cadaver head to impact. Stapp Car Crash Journal, Vol. 51, Issue 2, 2007, p. 17-80.
-
Yang B., Tse K. M., Chen N., Zheng Q. Q., Yang H. M., et al. Development of a finite element head model for the study of impact head injury. Biomed Research International, Vol. 2014, 2014, p. 408278.
-
Horgan T. J., Gilchrist M. D. Influence of FE model variability in predicting brain motion and intracranial pressure changes in head impact simulations. International Journal of Crashworthiness, Vol. 9, Issue 4, 2004, p. 401-408.
Cited by
About this article
The financial supports from the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20161522, BK20130977), Chinese Postdoctoral Science Foundation (Grant No. 2015M572243), Six Talent Peaks Project in Jiangsu Province, China (Grant No. JXQC-023) and the State Laboratory of Advanced Design and Manufacturing for Vehicle Body, China (Grant No. 31415008).
All authors were involved in the study. Tse co-conceived and co-developed the FE model for the manuscript. Lee co-conceived and co-developed the idea, and facilitated the gathering of contributors. Yang initiated the project, co-developed and co-refined the intellectual content, and wrote the first two drafts. Tang co-developed the idea, edited all drafts. Sun co-developed the idea and conducted the keyword search. Cao is the guarantor for the integrity of the article as a whole.
