Abstract
Drive system is one of most important key equipment to guarantee safe and stable operation in locomotive. With time variation, unpredictability and nonstationary, fault source of drive system is not obtained by traditional fault diagnosis method. Blind source separation is a kind of method on source signals separation under transmission channel unknown instance. The method of Blind source separation based on variable metric empirical mode decomposition is proposed. Intrinsic mode function is built, redundancy factors are reduced, and recurrent neural network is used to adaptive blind separation. The method is verified by data analysis of on-line measuring. The results show that separation efficiency is improved and unaffected with iteration time in the process of fault information separation, which will be better for further fundamental research and provide technique support for the locomotive.
1. Introduction
The heavy-haul railway is developing towards the large-carry, high-effective and low-cost, which has become the trend of global railway freight development. Transmission is the one of the most important equipment of heavy haul locomotive, which is the key mechanical equipment integrated mechanical and electronic, and precision decline seriously affected the safety and stability of the train in running process. In recent years, research on the locomotive transmission fault diagnosis has the great development. However, the problems such as misdiagnosis and misdiagnosis still exist. The main reason is the fault unpredictability, environmental diversity and polytropy. Which causes the increase of uncertain factors on transmission, and the dynamic linkage of key functional units is more obvious. As a result, the information of fault source cannot be accurately acquired, and the judgement on the accuracy recession is based on large amounts of miscellaneous device data. Therefore, how to obtain effective accuracy from the complex data is a severe challenge to fault identification and fault knowledge base management of locomotive transmission system.
Recently, many experts and scholars had made outstanding achievement in the mechanical fault diagnosis and engineering application research. According to wind power generation condition monitoring and fault diagnosis, Xuefeng Chen et al. [1] put forward planetary gear box modeling and dynamic behavior, researches on the method of fault feature extraction and accurate location, constructs the vibration standard model to conduct alarm threshold. In the process of signal processing and fault-feature-extraction method research, blind source separation has gained increasing acceptance in mechanical equipment state detection [2, 3]. Blind source separation is designed to remove the noises by relative independence of equipment fault signal and noise signal, and can collect the useful signals submerged in noises to easily found the faint fault information [4]. At present, however, a lot of faint information hides behind the massive data, it’s an urgent problem to achieve the separation of weak information effectively in low SNR [5-10].
Recently, a great many researchers had made further research on the theoretical research and application. Nguyen et al. [11] had researched single sensor information analysis by using PCA and SOBI, and subspace characteristics comparison under the fault state and normal state by constructing modal vector, which can complete industrial equipment health monitoring. Tse et al. [12] completed the fault isolation and identification on poor information of mechanical equipment by using blind equalization algorithm. Research on the method of blind source separation based on non-negative matrix factorization, and separated the convolution image hybrid by using multi-level decomposition. The method was based on non-negative matrix factorization, which can make the image decomposed no longer mixed. The final test results show that the method is more effective than blind source separation [13]. The separation effect is usually not obvious by using the independent component analysis (ICA) under the condition of bound constrain, Inan [14] adopts bound constrain algorithm with convolution form and corresponding algorithm to achieve the signal separation under bound constrain condition. The method can not only isolate independent sources signal, but also information source in the dimension of space and time.
At present, many universities and institutes have started to research on blind source separation widely, and have made great process in multi-information detection and fusion fault diagnosis. Chu Fulei [15] researched how to improve the accuracy of blind separation result evaluation, and has solve the inaccuracy of evaluation by using global weight matrix method and correlation coefficient. The method of phase-space reconstruction and singular value decomposition were proposed to realize underdetermined blind source separation by Shen Yongjun, and the test result shows that typical faults can be identified exactly on gear fault signal [16]. Yang Xiaokuo [17] researched to detect periodical poor signal with multiple frequencies by using characteristic vector, and poor signal was detected by establishing mixed signal matrix elements model. However, there is a problem that signal cannot be separated effectively when the different signals with the same period. With the unknown confusion matrix and mixing matrix, the method of solving eigenvector was proposed to reconstruct source signals by using irrelevance of each chaotic signal, and chaotic signal can be separated, however, there is error on solving correlation matrix under the analysis process [18]. A new method of global optimization signal-to-noise ratio blind source separation was proposed by Li Jie from Southwest jiaotong university, which was characterized by separable distinguishing, global optimization length of the sliding window was obtained by parameter modeling, and global optimization separative matrices was obtained by feature vector, the test result shows that the method is better than traditional methods on time-variable non-stationary signal blind source separation of high-speed train [19].
This paper presents a method of non-stationary and nonlinear poor information acquisition based on variable metric experience modal analysis. The method can establish intrinsic mode and remove redundant factors under the low signal to noise ratio, and self-adaption blind signals separate by using recurrent neural network. The problems of lacking information, the high noise and low separation efficiency will be avoided.
2. Method of blind source separation
According to statistic characteristics of source signal, blind source separation refers to the process of restoring or separating source signal by the signals of sensors under the source signal and transmission channel parameters are unknown [20]. Because the mathematical models between source signal and sensors was difficult to build, and often exist in the form of linear mixture and non-linear mixture, therefore, blind source separation is the inevitable choice for solving this problem. Blind source separation is often conducted based on the linear mixture model [21].
Set statistical independent source signals are detected by sensors after linearly instantaneous mixed, and each detection signal is the linearly mixed. Linear instantaneous mixed function represents:
Which, is hybrid parameter, is source signal, is the signal detected by sensors. , . The upper can also be expressed in vector form as:
Which, is mixed matrix, is source vector, and the elements is corresponds to base coefficient of transformation matrix.
Many noises were included between transmission channel and sensors, noise interference should be considered in a practical application, then the hybrid system model is:
where is noise vector, .
Blind source separation is seeking for the separation matrix of to transform , and transformed signal is considered as reliable assessment of source signal. The diagram is as shown Fig. 1.
Blind source separation based on independent component is to find optimal solution of the objective function by constructing objective function and classical optimization method. The whole process has a necessary iterative and convergent calculation. Finally, optimal separation matrix was obtained and the source independent component was isolated. Algorithm is illustrated as following examples.
Fig. 1Independent component analysis model

3. Dynamic self-adaptive blind source separation
The method of variable metric experience modal analysis is adaptive processing, which is based on characteristic time scale, and the complex signal function is decomposed into the sum of limited intrinsic mode functions. The characteristic scale parameter is a time span between two extreme points of the signals and can depict frequent. The intrinsic mode function (IMF) can characterize the local feature of signal respectively, and more accurate characteristic information could be got, as following conditions. (1) the whole signal is composed of some signals which satisfies certain characteristic time span, and the numbers of extreme points and zero-crossing points of each signal must equals; (2) the average value of upper envelope defined by maximum and lower envelope defined by minimum of each signal at any time must be zero. The problem of the low separation efficiency and obtaining weak fault signal difficultly caused by the nonlinear and non-stable can be solved by the above method. The flow chat is shown in Fig. 2.
(a) The maximum and minimum value of the acquired signals
is and respectively, 0, 1, 2,…, .
(b) Iterate , then screening for eliminating modal fluctuation.
(c) Let be the iteration screening signal, initialize
Fig. 2The flow chat of dynamic self-adaptive blind source separation
(d) Judge whether is intrinsic modal function according to the rules: if is accord with the IMF rules, is segmentation IMF; otherwise, starting at initial point of , and the maximum point is obtained in turn. Judge whether the time span of the two adjacent maximum points will meet . stands for the time corresponding maximum point. If is right, the maximum points will be recorded, otherwise, give it up. Obtain maximum points and minimum points of subsection signals met in turn.
(e) Using the cubic spline interpolating data to fit and , and solving the upper and lower envelopes to calculate the average curve :
(f) Screening calculation is made for mean curve , namely IMF.
(g) Using the recurrent neural network to make the minimization of IMF correlation, and solving mutual information by calculating probability density function, namely .
Under IMF constraints, the output will be reached to the minimum by adjusting network weights , and signal separation will be realized.
The method of dynamic intrinsic modal function is acquisition of the optimal intrinsic modal function in turn by cycle judgment , and finally efficient fault characteristic can be got. The method of recurrent neural network is to correlation analysis for fault characteristic, and dynamic adaptive blind separation can be realized by condition network weights. The above methods can realize the rapid diagnosis and maintenance for the key equipment of locomotive, thus the blindness of diagnosis is reduced and the efficiency of troubleshooting is improved.
4. Test analysis
By taking the six-shaft AC drive CRH D3C mixed traffic locomotive as the research object, as shown Fig. 3, the maximum power is 7200 KW, the maximum speed is 120 KM, and the gearbox is the Voith 553 type driving device. As shown in Fig. 4.
Fig. 3Harmonious-D3C mixed traffic locomotive

Fig. 4Drive system

The gear crack fault and normal state is measured respectively by building experimental platform of locomotive transmission system mechanical dynamic characteristic detection. The early crack state of gear is shown in Fig. 5. And the result is got by the method of blind source separation shown in Fig. 7.
Fig. 5Early crack fault of gear

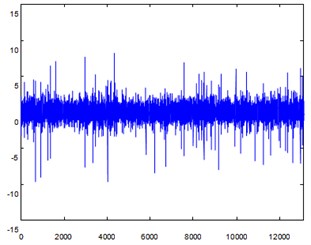
The test data shows that noise signal is mixed into the actual working of locomotive. The signal separation shown in Fig. 7 cannot reflect the early crack fault characteristic of gear by comparing Fig. 7 and Fig. 6. Therefore, the crack fault characteristics cannot be accurately diagnosed, which shows that the method of general blind source separation is not always available to weak fault recognition.
Fig. 6Early crack fault signal with noise
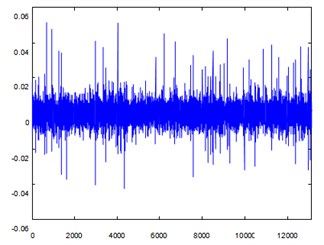
Fig. 7Signal separation of early crack fault signal with noise
Take the early crack fault shown Fig. 5 as example, research on the method of blind source separation based on dynamic intrinsic mode function and application in mixed-signal separation. The four intrinsic mode functions can be obtained by the iterative calculation of the crack faults signal. The results are shown in Fig. 8.
Fig. 8IMF 1, IMF 2, IMF 3, IMF 4
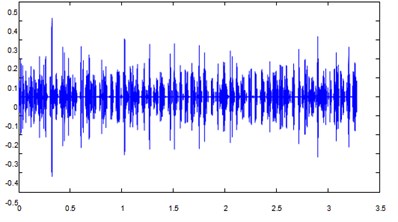
a) IMF 1
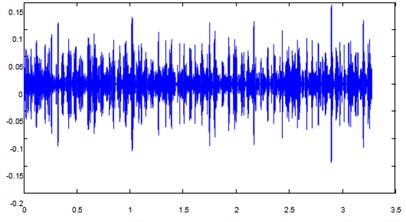
b) IMF 2
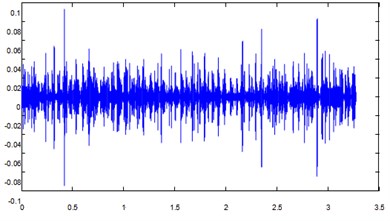
c) IMF 3
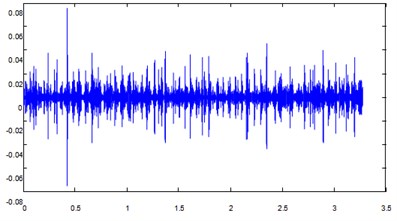
d) IMF 4
Fig. 9Separation signal
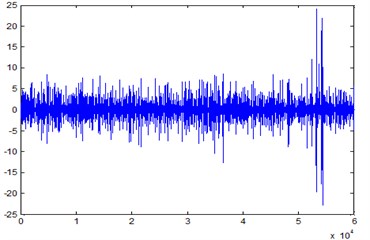
By adopting the method of RNN to correlation analysis for IMF, and dynamic adaptive blind separation can be realized by condition network weights. The separation result is shown in Fig. 9.
From the Fig. 9 it can be seen that the separation performance of the above method is better to non-stationary, nonlinear, time-variable aliasing weak signal. The fault characteristic can be separated clearly, and the extraction of weak fault feature is realized. The amplitude is uncertain because of amplitude’s uncertainty of blind separation. The experimental research of gear crack faults can show that the method of independent component analysis based on dynamic intrinsic mode functions is effective in transmission system gear fault diagnosis application. The accuracy, validity, and reliability of fault characteristics in mixed information can be verified by the method.
5. Conclusions
According to the problem of weak and uncertain information in drive system of locomotive, the method of self-adaption blind separation is proposed. The weak information is extracted by variable metric experience mode decomposition, and the redundant information is deleted. Self-adaption separation will be realized by the correlation of intrinsic mode function. The experiment shows that the iteration time can be reduced and the separation precision can be improved under the noise and uncertain state. The test result proves that the validity of the method by the simulating calculation and analysis of the locomotive transmission gear crack fault signal, which can provide a new way for railway transportation state detection and fault diagnosis.
References
-
Chen Xuefeng, Li Jimeng, Cheng Hang, et al. Research and application of condition monitoring and fault diagnosis technology in wind turbines. Journal of Mechanical Engineering, Vol. 47, Issue 9, 2011, p. 45-52.
-
Shi Xizhi Blind Signal Processing – Theory and Practice. Shanghai Jiao Tong University Press, Shanghai, 2008.
-
Chen Ximing, Huang Shuoyi Blind source separation: problem, principle and method. Electronic Information Warfare Technology, Vol. 23, Issue 2, 2008, p. 1-5.
-
Li Yi, He Yongyong, Li Zhinong, et al. Study on application of blind source separation and wavelet de-noising in rubbing fault acoustic signal analysis. Journal of Mechanical Strength, Vol. 27, Issue 6, 2006, p. 719-724.
-
Fabrizio G., Farina A. An adaptive filtering algorithm for blind waveform estimation in diffuse multipath channels. IET Radar Sonar, Vol. 5, Issue 3, 2011, p. 322-330.
-
Zhang Jie Blind source separation of non-stationary signals based on adaptive maximum signal-to-noise ratio method. Journal of Southwest Jiaotong University, Vol. 48, Issue 4, 2013, p. 769-775.
-
Wu Wenfeng, Chen Xiaohu, Su Xunjia Blind source separation of single-channel mechanical signal based on empirical mode decomposition. Journal of Mechanical Engineering, Vol. 47, Issue 4, 2011, p. 12-16.
-
Delvecchio S., Antoni J. Extraction of angle deterministic signals in the presence of stationary speed fluctuations with cyclostationary blind source separation. Mechanical Systems and Signal Processing, Vol. 27, 2012, p. 350-61.
-
Bonnardot F., Randall R. B., Guillet F. Extraction of second-order cyclostationary sources – application to vibration analysis. Mechanical Systems and Signal Processing, Vol. 19, Issue 6, 2005, p. 1230-44.
-
Clark F. S. P., Petragla M. R., Haddad D. B. A new initialization method for frequency-domain blind source separation algorithms. Signal Processing Letters, Vol. 18, Issue 6, 2011, p. 343-346.
-
Nguyen V. H., Rutten C., Golinval J.-C. Fault diagnosis in industrial systems based on blind source separation techniques using one single vibration sensor. Shock and Vibration, Vol. 19, Issue 5, 2012, p. 795-801.
-
Tse P. W., Zhang J. Y., Wang X. J. Blind source separation and blind equalization algorithms for mechanical signal separation and identification. Journal of Vibration and Control, Vol. 12, Issue 4, 2006, p. 395-423.
-
Hattay Jamel, Belaid Samir, Naanaa Wady Non-negative matrix factorisation for blind source separation in wavelet transform domain. IET Signal Processing, Vol. 9, Issue 2, 2015, p. 111-119.
-
Inan Huseyin A., Erdogan Alper T. Convolutive bounded component analysis algorithms for independent and dependent source separation. IEEE Transactions on Neural Networks and Learning Systems, Vol. 26, Issue 4, 2015, p. 697-708.
-
Li Zong, Feng Zhipeng, Chu Fulei A performance index of blind source separation based on improved crosstalk index. Journal of Vibration and Shock, Vol. 31, Issue 18, 2012, p. 83-88.
-
Shen Yongjun, Yang Shaopu, Kong Deshun New method of blind source separation in under-determined mixtures based on singular value decomposition and application. Journal of Mechanical Engineering, Vol. 45, Issue 8, 2009, p. 64-70.
-
Yang Xiaokuo, Wang Shuzhao, Wang Jun, et al. Method for detection of multi-frequency weak signal based on vector blind source separation. Chinese Journal of Sensors and Actuators, Vol. 21, Issue 8, 2008, p. 1393-1397.
-
Li Xuexia, Feng Jiuchao A blind separation method for chaotic signals. Physica Sinica, Vol. 56, Issue 2, 2007, p. 701-706.
-
Zhang Jie, Gao Hongli, Chen Chunjun, et al. Blind source separation method and application for nonstationary vibration signal of high speed train. Journal of Mechanical Engineering, Vol. 50, Issue 19, 2014, p. 97-104.
-
Chen Hao, Bai Lin, Zhou Zhiyu Discussion about development and application of blind source separation technology. Space Electronic Technology, 2013, p. 1-6.
-
Liu Ju, Nie Kaibao, He Zhenya On separability and separating method of nonlinear mixed signals. Journal of Electronics and Information Technology, Vol. 25, Issue 1, 2003, p. 54-61.
About this article
This work is partially supported by the National Natural Science Foundation of China (Grant Nos. 51405313, 11472179).
