Abstract
In every country, the construction of large steel bridges, such as cable-stayed bridges, is carried out actively, and the number of bridges has been progressively increasing. In the case of large steel bridges, inspections must be carried out every five years. Because frequent inspections of such bridges are required, working robots capable of performing inspections in difficult environments would be very useful. This paper proposes a vibration actuator with a very simple structure capable of movement on a magnetic substance via the inertial force of a mass–spring model. Through theoretical analysis using the energy method, it was determined that the vibration actuator is propelled by the difference between the frictional forces acting during the forward and backward motions of the actuator. The experimental and analytical results were compared, verifying the validity of the novel motion principle. Additionally, based on the asymmetric magnetic field that arises when a copper wire is asymmetrically wound around the iron core of an electromagnet, a method of increasing the magnetic field strength at one pole of the electromagnet is newly proposed. By attaching an iron plate to the iron core of the electromagnet, the effects of the resulting asymmetric magnetic field of the electromagnet on the actuator motion were examined. The experimental results indicate that the actuator is able to climb upward while pulling a load mass of 110 g. The maximum efficiency of the actuator was 20.5 % for an actuator pulling its own weight. The efficiency of the actuator with the attached iron plate was considerably greater than that without the iron plate.
1. Introduction
In every country, the construction of large steel bridges, such as cable-stayed bridges, is carried out actively, and the number of bridges has been progressively increasing. The inspection of large bridges with main towers exceeding 200 m in height or cable junctions damaged by strong winds is considerably difficult. Currently, large bridges with main towers exceeding 200 m in height, which require inspection every five years, are inspected by telescope. Therefore, it is not possible to confirm small-scale damage. To carry out this type of inspection, traffic regulation is necessary. In addition, ensuring the safety of the inspector is problematic. Furthermore, fatigue in bridges resulting from increasing traffic has become a considerable problem in recent years. It has been reported that the vibration of moving cars produces cracks in bridges. Therefore, it is important to determine the detailed state of cracks and stress in a bridge, necessitating the procurement of basic data for maintenance, such as repair or reinforcement data.
Based on the above considerations, working robots capable of inspection in difficult environments would be helpful in bridge inspections. A number of studies have investigated the mechanisms of a robot capable of climbing the vertical surfaces of large structures. Previously proposed adhesion methods for wall surface movement include the following: a permanent magnetic adhesion system coupled with a tracked locomotion mechanism [1, 2], the adhesive force of a suction cup manufactured from a sponge [3] or flexible rubber [4-8], control of the attractive force of an electromagnet inserted in it [9], a permanent magnet and an iron wheel [10, 11], a negative pressure using a pump [12-14], the wind force produced by a propeller [15], vibration of the many caps of a sucker to obtain mobile power [16, 17], a claw gripper [18-20], and adhesive materials [21, 22].
Mobile robots capable of wall climbing generally move at low speeds because of problems with controllability and their high weight resulting from their complex structures. A lightweight actuator with superior operability is expected in the inspection field. In previous studies, the authors proposed a novel vibration actuator capable of movement on a magnetic substance by coupling an electromagnetic force and mechanical vibration [23-26] and carried out theoretical analysis on this actuator [23, 24]. This vibration actuator has a very simple structure. Furthermore, direct drive is possible without link or reduction gear mechanisms because this actuator has high propulsion power. However, the theoretical analysis was limited to the movement of the actuator in the horizontal plane because the influence of the tilt angle of the magnetic substance had not been established. Therefore, a new motion principle was not completely established in these previous studies [23-26]. Moreover, to inspect large steel bridges, it is important to reduce the input power of the actuator and increase the propulsion force because the movement efficiency of this actuator is not very high. The authors suggested a method to improve the movement properties of the actuator by fundamentally changing its magnetic circuit [27]. It is necessary to design the vibration unit taking into account the tilt angle of the actuator.
In the present study, a vibration actuator with a very simple structure capable of movement on a magnetic substance by means of the inertial force of a vibration model was again considered. Through theoretical analysis using the energy method, it was determined that the vibration actuator is propelled by the difference between the frictional forces acting during the forward and backward motions of the actuator. The experimental and analytical results were compared, verifying the validity of the novel motion principle. Furthermore, based on the principle that an asymmetric magnetic pole is formed when copper wire is asymmetrically wound around the iron core of an electromagnet, a method of increasing the strength of the magnetic field at one pole of the electromagnet without changing the magnetic circuit was newly suggested. By attaching an iron plate to the iron core of an electromagnet, the effects of the resulting asymmetric magnetic field on the actuator motion were examined. The experimental results demonstrate that the maximum efficiency of an actuator pulling its own weight was 20.5 %. By simply attaching an iron plate to the actuator, the maximum efficiency was improved by a factor of approximately 1.58 compared with the actuator without an iron plate. The actuator was confirmed to be able to move on magnetic substances, such as iron rails, powered by only a function generator and a power amplifier.
2. Structure of vibration actuator
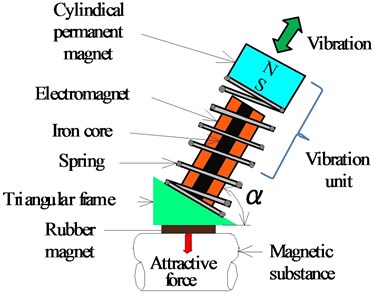
Fig. 1 shows an outline of the vibration actuator capable of movement on a magnetic substance, as developed in a previous study [26]. The vibration actuator consists of a permanent magnet, a translational spring, an electromagnet, a triangular acrylic frame, and a rubber permanent magnet attached to the bottom of the frame. The permanent magnet is a cylindrical NdFeB and is magnetized in the axial direction. Its dimensions are 12 mm in diameter and 5 mm in height. The surface magnetic flux density measured using a teslameter was 358 mT. The translational spring is a stainless steel compression coil with an outer diameter of 11 mm, a free length of 18 mm, and a spring constant of 2,178 N/m. The vibration unit was constructed using a translational spring and a cylindrical permanent magnet. The electromagnet was inserted into the translational spring. The rubber permanent magnet was attached to the bottom of the triangular frame, which was magnetized in the thickness direction. This rubber magnet has a length of 8.7 mm, a width of 15 mm, and a thickness of 2.7 mm. The average surface magnetic flux density measured using a teslameter was 116 mT. The vibration unit was inclined at an angle from the horizontal plane. The actuator has a height of 39.2 mm, a width of 15 mm, and a total mass of 13 g.
Fig. 1Structure of vibration actuator
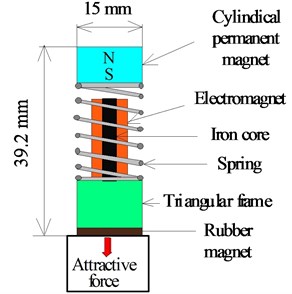
a) Front view
b) Side view
3. Motion analysis
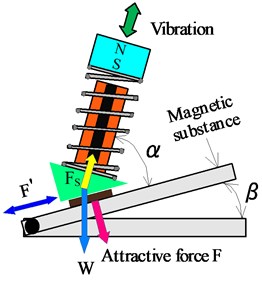
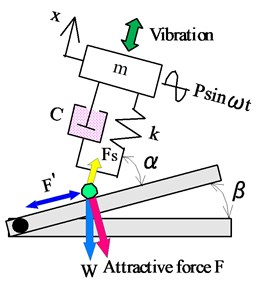
The vibration unit shown in Fig. 2(a) can replace the one-degree-of-freedom model shown in Fig. 2(b), which has spring constant , viscous damping coefficient , a cylindrical magnet of mass , and is displacement of the mass . is the attractive force applied by the rubber magnet when the actuator is placed on the magnetic substance; is the coefficient of friction; is the pulling force, which includes the weight of the actuator; is the frictional force; is the tilt angle of the vibration unit; and is the tilt angle of the magnetic substance. For the case in which the mass m is excited by a vibration generated by the electromagnet, the equation of translational motion can be written as:
where is the angular frequency, is the amplitude of the forced vibration, and is the time. The solution of Eq. (1), which represents the displacement of the mass , is given in terms of the amplitude and the phase of the displacement as:
The attractive force generated by the rubber magnet acts on the actuator when the magnetic actuator is placed on a magnetic substance. Accordingly, the actuator is able to vibrate. When the mass vibrates with amplitude , the generated force acting on the support part of the actuator is:
When the mass m of the vibration unit is displaced in the positive -direction, as shown in Fig. 3(a), the balance of the force in the direction along the magnetic substance can be written as:
Fig. 2One-degree-of-freedom mode
a) Vibration body
b) Equivalent model
Fig. 3Principle of locomotion
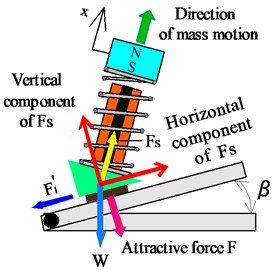
a) Forward motion
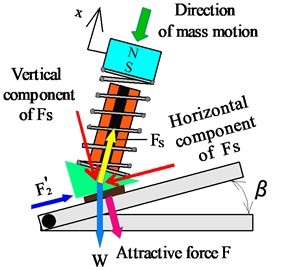
b) Backward motion
Conversely, when the mass m was displaced in the negative -direction, as shown in Fig. 3(b), the balance of the force in the direction along the magnetic substance can be expressed as:
In Eqs. (4) and (5), and are the frictional forces. By equalizing the dissipation energy by the frictional forces or and the elastic energy per vibration cycle, the forward displacement when mass m was displaced in the positive -direction and the backward displacement when the mass m was displaced in the negative -direction are obtained as:
where:
The real forward displacement of the actuator is regarded as the difference between the forward and backward displacements:
The value of gives the displacement of the actuator after one vibration cycle. The movement speed of the actuator can then be calculated by multiplying the driving frequency of the actuator by the displacement obtained from Eq. (8). Furthermore, the following equation can be obtained from Eqs. (6) and (8):
where:
Differentiating Eq. (9) with respect to , the optimum tilt angle of the vibration unit that maximizes displacement can be found by solving as:
The general solution of Eq. (11) is obtained using Cardano’s formula as:
where:
One in Eq. (11) is the solution of the demand.
In addition, because the actuator moves, it is necessary for the attractive force of the rubber permanent magnet holding the actuator to satisfy the condition:
In summary, the vertical and horizontal components of caused by the vibration unit alternate over one vibration period, as shown in Fig. 3. Therefore, the frictional force between the rubber magnet and the magnetic substance also changes over one vibration period. When the mass m is displaced in the positive -direction, the horizontal component of overcomes the frictional force , causing the actuator to move in the forward direction with displacement . Conversely, when the mass m is displaced in the negative -direction, the horizontal component of is only slightly larger than the frictional force , causing the actuator to move slightly in the backward direction with displacement . As a result, the vibration actuator is able to move in one direction with displacement . Thus, the vibration actuator is propelled by the difference between the frictional forces acting against the forward and backward motions.
4. Numerical calculation examples and comparison with experimental results
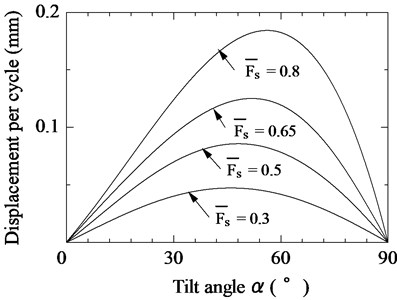
We carried out numerical calculations using a program that we coded in FORTRAN. The coefficient of friction, the tilt angle of the magnetic substance, and the pulling force including the weight of the actuator were set to 0.6, 0.1 mm, 0°, and 0.05, respectively. Fig. 4 shows the relationship between the tilt angle of the vibration unit and the displacement of the actuator per vibration cycle when was set to 0.3, 0.5, 0.65, or 0.8. The value of indicates the ratio of the generated force acting on the support part of the actuator to the attractive force of the rubber permanent magnet holding the actuator on the magnetic substance, as defined in Eq. (7). When the actuator is driven in the horizontal plane, has a considerable influence on the movement properties of the actuator. For each value of , there exists an optimal angle between 45° and 60° that maximizes .
Fig. 4Relationship between tilt angle of vibration unit and displacement per vibration cycle
Figs. 5-7 show the relationship between the tilt angle of the magnetic substance and the optimal tilt angle αopt of the vibration unit, as defined in Eq. (11), with 0.3, 0.5, and 0.8, respectively; 0.4, 0.6, 0.8, and 1.2, 0.1 mm; and 0.05. The tilt angle of the magnetic substance was varied from –90° (straight downward) to 90° (straight upward). As shown in Figs. 5-7, at magnetic substance tilt angles near 0°, the optimal tilt angle of the vibration unit was not affected by the value . However, at other magnetic substance tilt angles, the frictional force greatly influences the movement properties of the actuator. If is small, the tilt angle of the magnetic substance has a greater influence on the movement properties of the actuator. As the coefficient of friction increases, the movement efficiency of the actuator drastically decreases because of the increase in the dispersion energy. However, in this actuator, because differences between the downward and upward speeds of actuator increase when the coefficient of friction is small, an appropriate frictional force is necessary.
Fig. 5Relationship between tilt angle of magnetic substance and optimal tilt angle of vibration unit for various coefficients of friction (F¯s= 0.3)
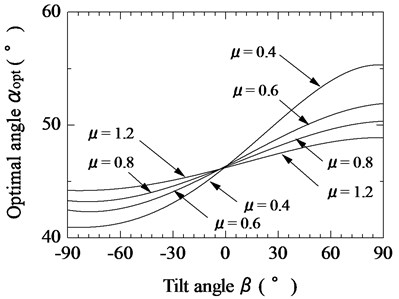
Fig. 6Relationship between tilt angle of magnetic substance and optimal tilt angle of vibration unit for various coefficients of friction (F¯s= 0.5)
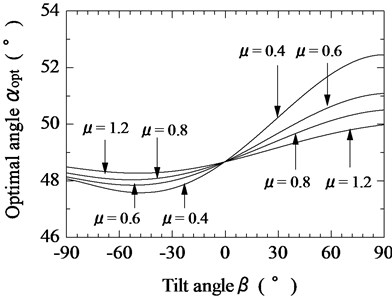
Fig. 7Relationship between tilt angle of magnetic substance and optimal tilt angle of vibration unit for various coefficients of friction (F¯s= 0.8)
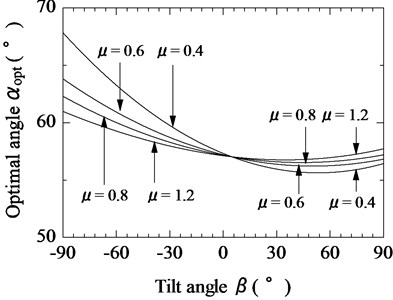
Fig. 8Relationship between tilt angle of magnetic substance and optimal tilt angle of vibration unit for various pulling forces (F¯s= 0.3)
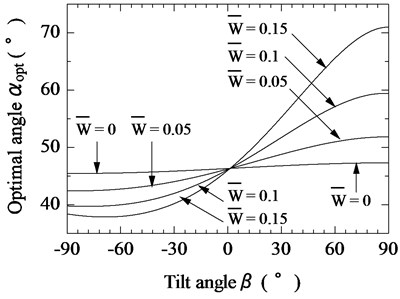
Fig. 9Relationship between tilt angle of magnetic substance and optimal tilt angle of vibration unit for various pulling forces (F¯s= 0.5)
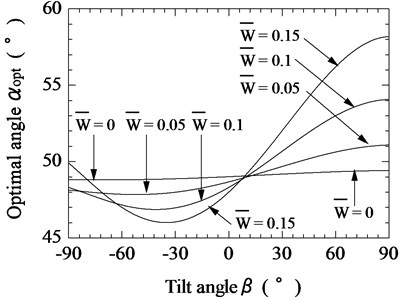
Fig. 10Relationship between tilt angle of magnetic substance and optimal tilt angle of vibration unit for various pulling forces (F¯s= 0.8)
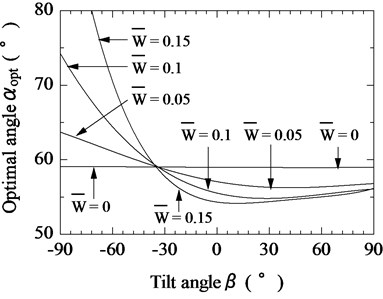
Figs. 8-10 show the relationship between the tilt angle of the magnetic substance and the optimal tilt angle of the vibration unit for 0.3, 0.5, and 0.8, respectively; 0.1 mm; 0.6; and 0, 0.05, 0.1, and 0.15. When the pulling force increased, variations in the optimal angle became more pronounced. It was determined that the value of should be set between 55° and 60° when there is heavy load on the actuator.
Based on the above results, and considerably influence the movement properties of the actuator. Accordingly, selecting appropriate values for the attractive force of the rubber permanent magnet and the coefficient μ of friction is very important.
Fig. 11Experimental apparatus
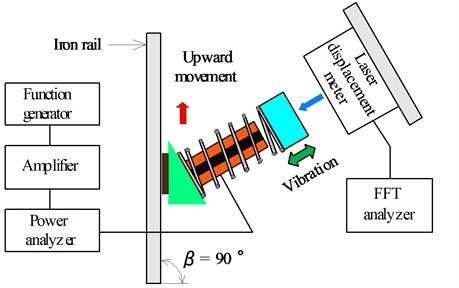
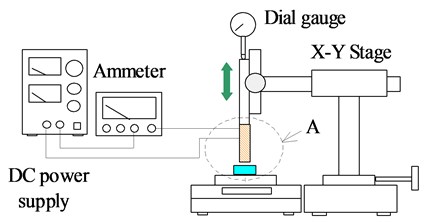
An experiment was conducted to verify the validity of the theoretical analysis performed in this study. Fig. 11 shows the experimental apparatus. The vibration actuator shown in Fig. 1 was produced. An iron rail with a width of 50 mm, a thickness of 50 mm, and a length of 400 mm was used as the magnetic substance. The experimentally measured coefficient of friction between the iron rail and the rubber permanent magnet was 0.715. The spring constant for the vibration unit is 2,178 N/m, as mentioned above. The frequency response of the vibration unit was measured, and the viscous damping coefficient was calculated to be 0.055 by using the half-power bandwidth method. The attractive force F of the rubber magnet measured using the force gauge was 3.12 N. The total mass of the actuator is 13 g, which yields 0.408. The coefficient of friction and the attractive force were fixed during the experiment. The tilt angle of the vibration unit was set to 60° based on the above results. The actuator was driven by a resonance frequency of 96 Hz. When the actuator was moved upward ( 90°), the vibration amplitude of the moving actuator was measured using a laser displacement meter and a fast Fourier transform (FFT) analyzer. During the measurement, and were changed by changing the input power. and were calculated from the measured amplitude using Eq. (7). By multiplying the drive frequency by the value of calculated using Eq. (8), the theoretical speed of the actuator was obtained. Table 1 and Fig. 12 compare the theoretical and experimental results, which showed good agreement. Error between theoretical and experimental values is due to the coefficient of friction is changed by the position of the iron rail. Thus, the validity of the theoretical analysis was demonstrated. This vibration actuator moves intermittently while repeating forward and backward movements during each vibration cycle. In this paper, the motion principle of the actuator has been completely established.
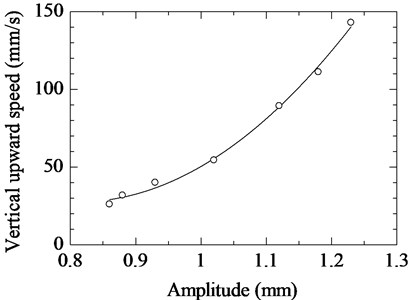
On the other hand, Fig. 13 shows the relationship between the input power into the electromagnet and the amplitude of the vibration unit. The amplitude the vibration unit increases linearly when the input power increases. Furthermore, the increase in the amplitude about a secondary increase in vertical upward speed as shown in Fig. 14. It is expected that the efficiency of the actuator depends on the electromagnet force, on account of this actuator moves using elastic energy.
Table 1Theoretical and experimental data
Amplitude (mm) | (mm) | Theoretical speed (mm/s) | Experimental speed (mm/s) | Input power (mW) | |
0.86 | 0.6 | 0.000335 | 28.1 | 26.04 | 105 |
0.88 | 0.613 | 0.00035 | 30.4 | 31.8 | 140 |
0.93 | 0.65 | 0.000393 | 37.9 | 40 | 175 |
1.02 | 0.714 | 0.000474 | 55.2 | 54.4 | 198 |
1.12 | 0.782 | 0.000568 | 81.1 | 89.3 | 245 |
1.18 | 0.822 | 0.000625 | 111.1 | 111.1 | 278 |
1.23 | 0.857 | 0.000683 | 143.9 | 142.9 | 300 |
Fig. 12Comparison of theoretical and experimental results
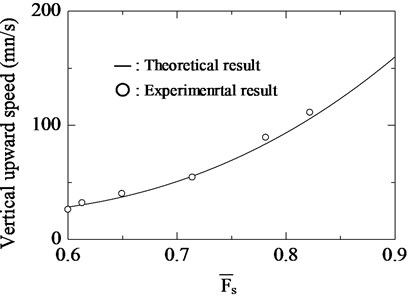
Fig. 13Relationship between input power and amplitude of vibration unit
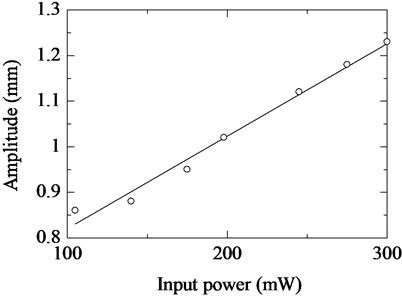
Fig. 14Relationship between amplitude of vibration unit and vertical upward speed
5. Examination of increase in magnetic force caused by attaching iron plate
A novel vibration actuator capable of movement by means of an inertial force was proposed and tested by the present authors in a previous study [26]. However, the movement efficiency of the actuator was not very high. An effective method of improving efficiency is newly proposed in this paper.
When a copper wire is symmetrically wound around an iron core to create an electromagnet, a magnetic field with the same strength at each magnetic pole of the iron core is formed. Conversely, when a copper wire is asymmetrically wound around an iron core, an asymmetric magnetic field is formed. The strength of the magnetic field at one pole of the electromagnet can be increased by utilizing asymmetric windings, as mentioned above. A method of increasing the propulsion power of the actuator was suggested in this paper.
Fig. 15 shows the proposed actuator with an iron plate attached to one end of the iron core of the electromagnet. The electromagnet produces an asymmetric magnetic field as a result of the connection between the iron plate and the iron core.
Based on the results obtained in a previous study [26], an optimized electromagnet with an iron core of 3.5 mm in diameter and 17 mm in length and 540 turns of 0.2-mm copper wire was used. Before the experiment was performed, the magnetic flux density of the electromagnet was calculated using two-dimensional finite element analysis software. It was confirmed by numerical simulation that the magnetic flux density of the electromagnet increased when the iron plate was attached to the iron core. Based on these simulation results, iron plates of three sizes were used in the experiment. The sizes and masses of the iron plates are listed in Table 2, where Type I is the case without an iron plate and Types II, III, and IV indicate the three iron plates of different sizes.
Fig. 15Electromagnet with attached iron plate
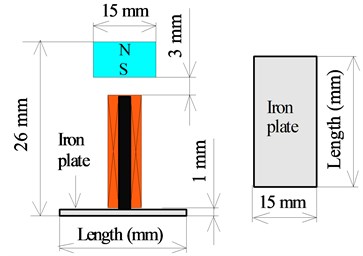
Table 2Sizes and masses of iron plates
Length (mm) | Width (mm) | Thickness (mm) | Mass (g) | |
Type I | 0 | 0 | 0 | 0 |
Type II | 15 | 15 | 1 | 1.8 |
Type III | 30 | 15 | 1 | 3.6 |
Type IV | 45 | 15 | 1 | 5.4 |
Fig. 16Measurement of magnetic force
a) Measurement of magnetic force
b) Detail of section A
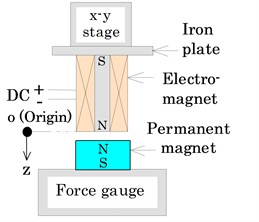
The magnetic force increased linearly when the magnetic flux density of the electromagnet increased. It was hypothesized that increasing the magnetic force would cause a secondary increase in speed because the vibration actuator is an elastic energy-type actuator. Therefore, before the vibration actuator was produced, the magnetic force for the electromagnet with an iron plate attached to one edge was measured. An experiment was conducted using the apparatus shown in Fig. 16(a). A direct current of 0.3 A was applied to the electromagnet during the measurement. The origin was taken as the tip of the electromagnet, and the position in the -direction was measured as shown in Fig. 16(b). The clearance threshold between the iron core and the permanent magnet was set to 3 mm. In the vibration unit, a forced harmonic vibration was generated by the attractive and repulsive forces. Accordingly, the attractive and repulsive forces were measured when the clearance was less and more than 3 mm, respectively.
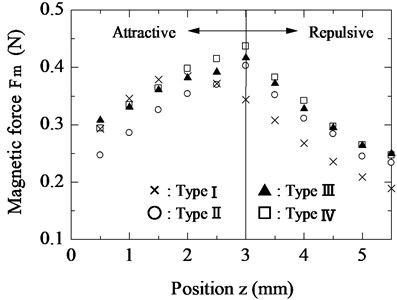
Fig. 17 shows the relationship between the position and the magnetic force measured using the force gauge for all iron plate sizes considered in this experiment. The average value of the measured magnetic force increased with increasing plate size; the magnetic forces for the Type II, III, and IV iron plates were 1.05, 1.13, and 1.16 times that of Type I, respectively. From these results, as the size of the iron plate increased, the magnetic force increased; however, the weight of the actuator also increased with increasing iron plate size, decreasing its movement properties. Therefore, the Type III iron plate was used in the next experiment in this study.
Fig. 17Relationship between position and force for different iron plate sizes
6. Locomotion characteristics of vibration actuator
Fig. 18 shows the experimental apparatus and the vibration actuator. The Type III iron plate was attached to one side of the electromagnet, and a prototype of the vibration actuator was produced. The actuator has a height of 40.5 mm and a width of 30 mm. The total mass of the vibration actuator is 17 g. An iron rail with a width of 50 mm, a thickness of 50 mm, and a length of 400 mm was used, as mentioned in the previous section. The vibration unit was driven at the resonance frequency of 96 Hz using a function signal generator and an amplifier. During the measurement, the coefficient of friction was 0.715, and the attractive force was 3.12 N. The tilt angle of the vibration unit was set to 60°, and the tilt angles and of the iron rail were varied, as shown in Fig. 19.
Figs. 20 and 21 show the relationship between the tilt angles and of the iron rail with respect to the horizontal plane and the speed of the actuator. In these figures, the solid and dashed lines indicate the cases with and without the iron plate attached to the electromagnet, respectively. Here, the input power into the electromagnet was set to 150, 200, and 250 mW. The tilt angles and of the iron rail were varied between –90° (downward) and 90° (upward).
In Figs. 20 and 21, because the attractive force F of the support part changed as a result of the influence of the weight of the vibration actuator, for 0°, the speeds of the two movement types were different. In addition, for 90°, the movement was a wall-climbing movement. This vibration actuator is capable of both slide-on-ceiling and wall-climbing motions.
In Fig. 20, when the power input into the electromagnet without the iron plate was 200 mW, its average speed was 49.7 mm/s as the tilt angle was varied from –90° to 90°. Furthermore, its average speed was 49.9 mm/s in Fig. 21. The excitation force of the actuator with the attached Type III iron plate was 1.13 times that without the plate, as mentioned in the previous section. Because this vibration actuator is an elastic energy-type actuator, the elastic energy of the actuator with the attached Type III iron plate is 1.27 times that without the iron plate. From the results in Figs. 20 and 21, the average speeds of the actuator with the iron plate when and were varied between –90° and 90° were 63.5 and 63.6 mm/s, respectively, at an input power of 200 mW. When a Type III iron plate was attached to the actuator, the speed increased by approximately 1.27 times in comparison with the case without the iron plate. It was proven that an increase in the magnetic force causes a secondary increase in speed.
Fig. 18Experimental apparatus and vibration actuator

Fig. 19Vibration actuator moving on iron rail
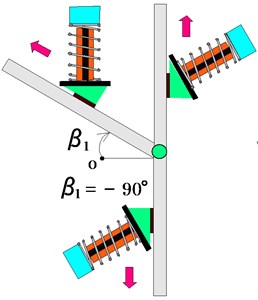
a) Horizontal plane
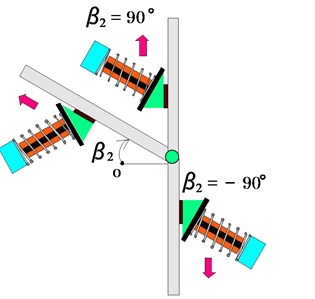
b) Slide-on-ceiling plane
Fig. 20Relationship between tilt angle β1 of magnetic substance and speed of actuator

Fig. 21Relationship between tilt angle β2 of magnetic substance and speed of actuator
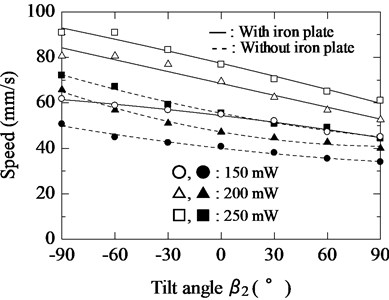
Fig. 22 shows the relationship between the mass of the load of the actuator and the speed of the upward movement at input powers of 150, 200, and 250 mW. The load was attached to the actuator with a string. In this figure, the solid lines indicate the cases with the iron plate attached to the electromagnet at various input powers, and the dashed line indicates the case without the iron plate at an input power of 200 mW. This figure indicates that the actuator was able to climb upward at 36 mm/s while pulling a load of 110 g when the input power was 250 mW.
The solid and dashed lines in Fig. 23 show the relationship between the load mass and the efficiency including own-weight of the actuator when with and without the iron plate, respectively. The input power of the electromagnet was set to 150, 200, and 250 mW. The efficiency is expressed as:
where is the total mass of the actuator, is the mass of the load, is the upward speed, is the acceleration due to gravity, and is the input power.
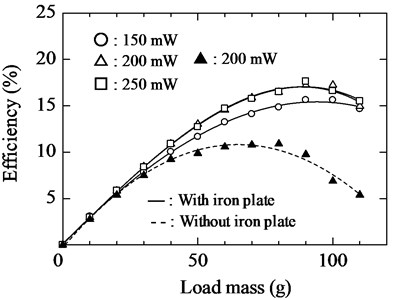
The solid and dashed lines in Fig. 24 show the relationship between the load mass and the efficiency excluding own-weight of the actuator when with and without the iron plate, respectively. The input power of the electromagnet was set to 150, 200, and 250 mW. From the measurement results, the maximum efficiency of the actuator was 17.2 % for the case excluding the weight of the iron plate and 20.5 % for the case including it. By simply attaching an iron plate, the maximum efficiency was improved by a factor of approximately 1.58 in comparison with the actuator with no attached iron plate. This efficiency also demonstrates that as the linear and rotational motor when the actuator was driven on a horizontal plane.
Fig. 22Relationship between load mass and upward speed
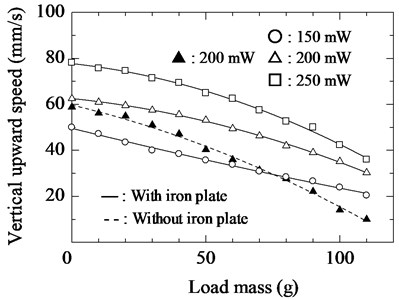
Fig. 23Relationship between load mass and efficiency
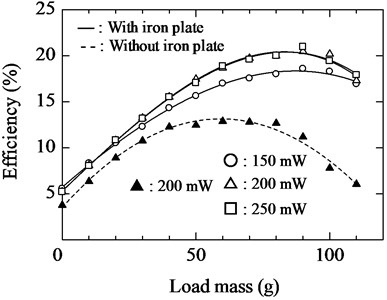
Fig. 24Relationship between load mass and efficiency
7. Conclusions
A novel vibration actuator capable of movement by means of an inertial force has been proposed. Through theoretical analysis using the energy method, numerical calculations were carried out. The experimental and analytical results were compared and found to be in good agreement, thus verifying the validity of the novel motion principle.
Furthermore, based on the fact that an asymmetric electromagnet produces an asymmetric magnetic field, a method of increasing the magnetic field strength at one pole of the electromagnet by attaching an iron plate was newly proposed. The experimental results reveal that this vibration actuator is able to pull a load mass of 110 g. The maximum efficiency of the actuator was 17.2 % without the iron plate and 20.5 % for the case with the iron plate to calculate self-propellant efficiency when the input power of the electromagnet was 200 mW. By simply attaching an iron plate, the maximum efficiency was improved by a factor of approximately 1.58 in comparison with the case without the iron plate. The actuator was confirmed to be able to operate when powered by only a function generator and a power amplifier. Because the actuator is compact and lightweight and has good mobility, it is applicable to the inspection of large steel bridges.
To allow multiple micro-cameras to be loaded on the proposed vibration actuator, which must pull numerous cables over distances of 200 m to inspect large bridges, a propulsion force of over 2.5 N is necessary. In the future, the improvement of the propulsion power by the grouping of the actuator will be performed. Moreover, the vibration actuator must be capable of climbing steps.
When the inspection of large bridges is performed, in consideration of a case in which the surface condition such as corrosion is different, the attractive force must be changed by replacing the rubber magnet with the electromagnet. Therefore, it is necessary to modify structure of the support part. Finally, we think that this actuator can be applied to the wall climbing robot for inspection by improving the characteristics of movement. Future research will be directed toward these goals.
References
-
Shen W., Gu J., Shen Y. Permanent magnetic system design for the wall-climbing robot. IEEE International Conference on Mechatronics and Automation, 2011, p. 2078-2083.
-
Lee G., Park J., Kim H., Seo T. W. Wall climbing robots with track-wheel mechanism. IEEE International Conference on Machine Learning and Computing, 2011, p. 334-337.
-
Fukuda T., Matsuura H., Arai F., Nishibori K., Sakauchi H., Yoshi N. A study on wall surface mobile robots. Transactions of the Japan Society of Mechanical Engineers, Vol. 58, Issue 550, 1992, p. 286-293.
-
Kawasaki S., Kikuchi K. Development of a small legged wall climbing robot with passive suction cups. International Conference on Design Engineering and Science, 2014, p. 112-116.
-
Yoshida Y., Ma S. A wall-climbing robot without any active suction mechanisms. IEEE International Conference on Robotics and Biomimetics, 2011, p. 2014-2019.
-
Miyake T., Ishihara H., Yoshimura M. Basic studies on wet adhesion system for wall climbing robot. IEEE/RSJ International Conference on Intelligent Robots and Systems, 2007, p. 1920-1925.
-
Apostolescu T. C., Udrea C., Duminica D., Ionascu G., Bogatu L., Cartal L. A. Development of a climbing robot with vacuum attachment cups. International Conference on Innovations, Recent Trends and Challenges in Mechatronics, 2011, p. 258-267.
-
Akhtaruzzaman M., Samsuddin N., Umar N., Rahman M. Design and development of a wall climbing robot and its control system. International Conference on Computer and Information Technology, 2009, p. 309-313.
-
Suzuki M., Hirose S. Proposal of swarm type wall climbing robot system anchor climber and development of adhering mobile units. The Robotics Society of Japan, Vol. 28, Issue 5, 2010, p. 614-623.
-
Khirade N., Sanghi R., Tidke D. Magnetic wall climbing devices – a review. International Conference on Advances in Engineering and Technology, 2014, p. 55-59.
-
Kim J. H., Park S. M., Kim J. H., Lee J. Y. Design and experimental implementation of easily detachable permanent magnet reluctance wheel for wall-climbing mobile robot. Journal of Magnetics Vol. 15, Issue 3, 2010, p. 128-131.
-
Kim H., Kim D., Yang H., Lee K., Seo K., Chang D., Kim J. Development of a wall-climbing robot using a tracked wheel mechanism. Journal of Mechanical Science and Technology, Vol. 22, 2008, p. 1490-1498.
-
Subramanyam A., Mallikarjuna Y., Suneel S., Kumar L. Bhargava Design and development of a climbing robot for several applications. International Journal of Advanced Computer Technology, Vol. 3, Issue 3, 2011, p. 15-23.
-
Panich S. Development of a climbing robot with vacuum attachment cups. Journal of Computer Science, Vol. 6, Issue 10, 2010, p. 1185-1188.
-
Jae-Uk S., Donghoon K., Ong-Heon J., Hyun M. Micro aerial vehicle type wall-climbing robot mechanism. IEEE RO-MAN International Symposium on Robot and Human Interactive Communication, 2013, p. 722-725.
-
Wang K., Wang W., Li D., Zong G., Zhang H., Zhang J., Deng Z. Analysis of two vibrating suction methods. IEEE International Conference on Robotics and Biomimetics, 2008, p. 1313-1319.
-
Wang W., Wang K., Zhang H., Zhang J. Internal force compensating method for wall-climbing caterpillar robot. IEEE International Conference on Robotics and Automation, 2010, p. 2816-2820.
-
Xu F., Wang X., Jiang G. Design and analysis of a wall-climbing robot based on a mechanism utilizing hook-like claws. International Journal of Advanced Robotic Systems, Vol. 9, Issue 261, 2012, p. 1-12.
-
Funatsu M., Kawasaki Y., Kawasaki S., Kikuchi K. Development of cm-scale wall climbing hexapod robot with claws. International Conference on Design Engineering and Science, 2014, p. 101-106.
-
Provancher W., Jensen-Segal S., Fehlberg M. ROCR: an energy-efficient dynamic wall-climbing robot. IEEE Transaction on Mechatronics, Vol. 16, Issue 5, 2011, p. 897-906.
-
Kute C., Murphy M., Menguc Y., Sitti M. Adhesion recovery and passive peeling in a wall climbing robot using adhesives. IEEE International Conference on Robotics and Automation, 2010, p. 2797-2802.
-
Unver O., Sitti M. Tankbot: a miniature, peeling based climber on rough and smooth surfaces. IEEE International Conference on Robotics and Automation, 2009, p. 2282-2287.
-
Yaguchi H. Prototype of a cable-less magnetic micro-mover. Journal of The Magnetics Society of Japan, Vol. 30, Issue 2, 2006, p. 258-263.
-
Yaguchi H., Suzuki H. Moving properties of a cable-less magnetic micro actuator. Journal of The Magnetics Society of Japan, Vol. 31, Issue 2, 2007, p. 143-147.
-
Yaguchi H., Sakuma S. A new type of magnetic actuator capable of wall-climbing movement using inertia force. Journal of Engineering, Vol. 2014, 2014, p. 1-9.
-
Yaguchi H., Sakuma S. A novel magnetic actuator capable of free movement on a magnetic substance. IEEE Transaction on Magnetics, Vol. 51, Issue 11, 2015, p. 8206204.
-
Yaguchi H., Sakuma S. Improvement of a magnetic actuator capable of movement on a magnetic substance. IEEE Transaction on Magnetics, 2016, https://doi.org/10.1109/TMAG.2016.2533433.
