Abstract
Comparison of the approximation performance of the ultrasonic reflections by simple model functions used in blind deconvolution is presented. New model function was proposed where causality of the signal is easily modelled without the need for piecewise-linear equations. Parameter estimation technique was developed. Performance investigation was done for three model functions using four experimentally collected ultrasonic signals under different signal filtering conditions.
1. Introduction
Ultrasonic inspection is offering a useful tool for material mechanical integrity testing [1-3]. Pulse-echo mode of non-destructive testing is considered in this research. Acoustic wave traveling in the test material encounters the reflection from inhomogeneities (defects) along the travel path [4]. Such echoes produced carry the information about the location of the defect as the time of flight (ToF) and the severity of the defect or even mechanical properties as the reflection amplitude. ToF can be converted to distance if propagation velocity is known and the reflection amplitude can be converted to mechanical impedance which in turn is related to density and velocity (stiffness) [3, 4]. Estimation of the aforementioned parameters for the single echo does not present significant problem, but when several reflectors are present along the wave path the reflections pile up obscuring the reliable estimation of the echoes parameters [5]. If probing signal is of indefinite bandwidth such problem does not exist, but bandwidth is always limited in practice [6, 7]. Furthermore, limited bandwidth is usually desirable, because signal acquisition system requirements can be relaxed [8], attenuation of ultrasound at high frequencies produces structural noise and signal degradation [9]. Deconvolution is used to address this problem [10-12]. It is based on assumption that reflections are sparse (based on usual defects structure which present themselves as layers or distributed cavities) and that every reflection is a time and amplitude translated copy of the original probing signal (reference). Inverse filtering [13, 14] is dividing the received signal by reference in frequency domain in order to produce the impulse response of the media being probed. Unfortunately, very high signal-to-noise ratio (SNR) is needed in order to obtain acceptable results. Wiener filtering [13] can be used to address the problem, but it does not offer the decomposition of the signal into ToF and corresponding amplitudes. Iterative deconvolution techniques allow for efficient signal decomposition either processing one reflection at a time or several reflections simultaneously [6, 10, 12, 15]. Yet, production of the reference signal constitutes a major problem in all deconvolution methods [5, 6, 16, 17]. Signal spectral content is altered along the propagation path or at reflection interface [4]. Together with noise present, this significantly degrades the results of deconvolution. Blind deconvolution [17, 18] is offering a production of reference signal using some simple mathematical model function, Gabor (harmonic oscillation with Gaussian envelope) being the most frequently used [6, 19]. Result of such deconvolution significantly improves the SNR, adapts the signal spectral content changes and significantly reduces the required amount of computer memory needed to store or transmit the acquired data [20] by compressive sensing. Analytical processing is required for the estimation of the fitting function parameters [6, 10-12, 17, 19]. Unfortunately, Gabor function goes against causality principle of ultrasonic inspection and is only suitable for narrowband signals. Attempts to split the envelope slope into two [16, 17] are not favored since analytical processing of such function is more complicated. The goal of the presented investigation was to compare the approximation performance of the model functions. New model function was proposed where the right-tailed asymmetry (causality) of the signal is easily modelled without the need for the piecewise-linear equations. Comparison of three model functions was done using four experimentally collected ultrasonic signals.
2. The ultrasonic signals
As it was mentioned above, narrowband signal is easy to approximate by Gabor function [6, 19], yet the wideband case is the more complicated. Therefore, investigation was concentrated on wideband signals. Several wideband ultrasonic transducers were used to collect the representative signals: i) spherically focused 5 MHz center frequency and 64 % bandwidth transducer IRY405 from NDT transducers PLL (further labelled 5F); ii) spherically focused 10 MHz center frequency and 71 % bandwidth transducer IRY210 from NDT transducers PLL (labelled 10F); iii) composite, unfocused 5 MHz center frequency and 86 % bandwidth transducer TF5C6N-E from Doppler Electronic Technologies (further – 5U) and iv) composite, unfocused 10 MHz center frequency and 66 % bandwidth transducer TF10C6L from Doppler Electronic Technologies (further – 10U). The polished 30 mm height and 20 mm diameter stainless steel cylinder was immersed in water tank (refer Fig. 1) and reflections collected using ultrasonic data acquisition system [8].
Fig. 1Experiment setup used for ultrasonic signals collection
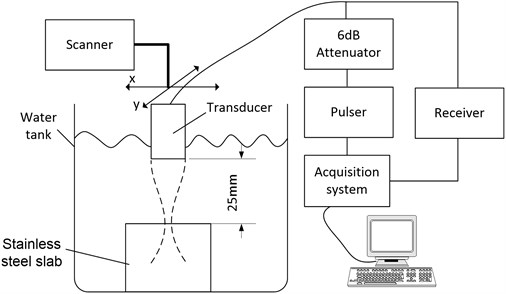
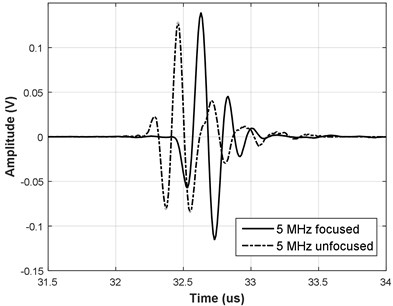
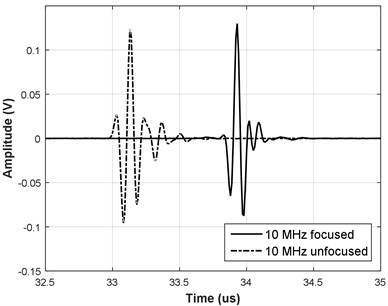
Fig. 2A-scans of the reflections for a) 5 MHz transducers and b) 10 MHz transducers
a)
b)
Transducer excitation was done using a unipolar pulser, using 10 V rectangular pulse of 50 ns duration for 10 MHz transducers and 100 ns duration for 5 MHz transducers. Receiver was 0.5-30 MHz bandwidth with 30 dB gain. One thousand A-scans with steel slab reflection present were collected and averaged to reduce the noise. A-scans of such reflections for the corresponding transducers are presented in Fig. 2.
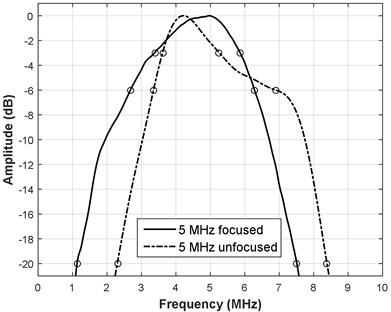
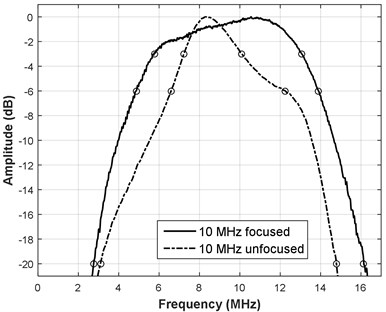
Spectrums of the corresponding reflections have been calculated using the discrete Fourier transform (DFT). Refer Fig. 3 for corresponding reflections spectrums and indications of –3 dB, –6 dB and –20 dB bandwidth. These bandwidth values were later used for selecting the passband parameters in additional signal filtering.
Fig. 3Reflection spectrum for a) 5 MHz transducers and b) 10 MHz transducers
a)
b)
Unfocused type transducers are composite type, and have significant bandwidth therefore their spectral temporal and spectral response is more complicated. Focused transducers are of single crystal type so their response is closer to simple resonant tank. Signals were stored for further processing.
3. Candidate functions
Ultrasonic reflection signal can be approximated as Gaussian modulated cosine or Gabor function [19]:
where is amplitude, is the width of the envelope of the echo, is the time of flight (ToF), is center frequency and is phase. These function parameters are closely related to the properties of ultrasonic signal [20]. The amplitude can be related to the size of the reflector, and are related to the used transducer, ToF represents the temporal (as well as spatial) position of the reflector, accounts for the distance, impedance, size, and orientation of the reflector. These parameters are expressed as vector :
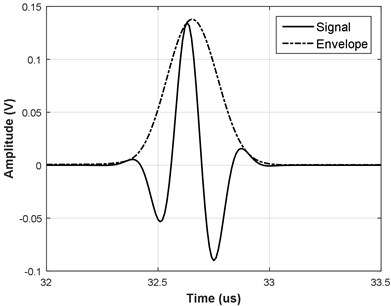
Example of Gabor function is presented in Fig. 4. Envelope was obtained using Hilbert transform. It can be seen that such signal exhibit close similarity to Fig. 2 yet are lacking the asymmetry and causality. The decomposition of the signal using the Gaussian function can be compromised if received echoes are more complex [20]. New, Gaussian Chirplet model with additional chirp sinusoidal component was proposed in [6, 17]:
where is the linear chirp rate. The parameters are expressed as vector :
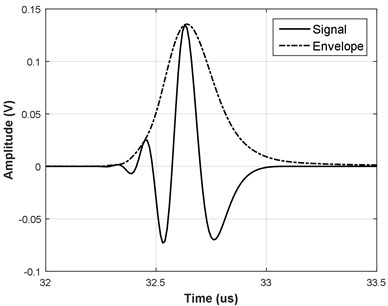
Example of Gaussian Chirplet model is presented in Fig. 4.
Fig. 4a) Example of Gabor and b) Gaussian Chirplet functions
a)
b)
Unfortunately, despite this being better than simple Gaussian, the envelope of this model is still symmetric with respect to its peak position. In this study we introduce a new echo model that has the asymmetric envelope component with chirp as carrier:
where is asymmetry coefficient. Envelope function was derived from lognormal distribution function with the modification of the tipping point so it corresponds to ToF position . Corresponding parameters are presented as vector :
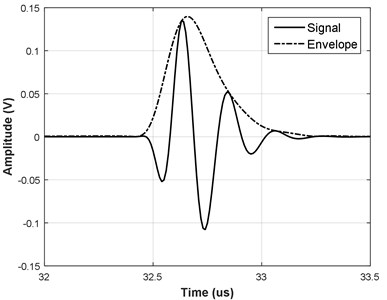
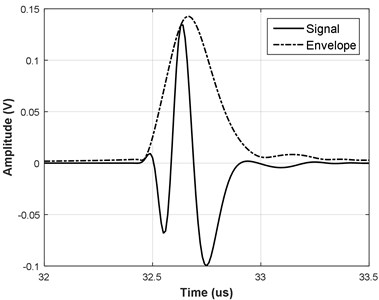
Refer to Fig. 5 for representative examples of the new proposed function.
Fig. 5Example of new function with a) linear frequency modulation and b) without
a)
b)
Essential, that new function obeys the causality principle: analyzing Eq. (5) one can see that time axis and so the signal can exist only from certain temporal position in front of . Same can be deduced from Fig. 5 analysis: there is no signal energy beyond the certain point in front of the signal. Furthermore, asymmetry of the signal is produced on uniform time axis, without the need for piecewise approximation as per [16, 17].
4. Estimation of the parameters of the approximating functions
It is important to estimate parameters of a model with least computational effort and accurately. In [19] Demirli and Saniie used Gauss-Newton algorithm to obtain the ultrasonic echo parameters. However, the drawback of this algorithm is that the results of Gauss-Newton algorithm can be local optimum rather than global optimum. The reason for this is that Gauss-Newton algorithm depends on initial solution. An Artificial Bee Colony (ABC) algorithm was introduced in 2015 to overcome those drawbacks [21, 22].
Deconvolution can be divided into two minimization problems: i) “pure” deconvolution where signal is treated as convolution of test object reflectivity function with probing (reference) signal [10-12] and ii) reference signal production [18, 19, 23]. Deconvolution is the optimization problem that uses sparse deconvolution methods such as matching pursuit, Prony model or orthogonal matching pursuit in order to deconvolve the mixed data [5, 6, 15, 16]. In general, reference signal can be treated as time-invariant here and can be pre-recorded from some interface exhibiting strictly step response. Unfortunately, sometimes the reference signal is not available or is time-variant. In such case second optimization problem arises which was named blind deconvolution [17-20, 22, 23]. Here signal echo is simulated as simple mathematical function whose model parameters can be iteratively adjusted. In current research we only concentrate on reference signal derivation, adjusting the model parameters. Adjustment can be carried out using iterative Newton method. We suggest different approach with following improvements: initially (ToF), (amplitude) and (phase) are directly derived using the correlation processing:
where is the complex correlation function:
where is the original signal, is the model function Eq. (5) without and components and is the model function Eq. (5) without and components and sin instead cos. Both model and the original signals are discrete versions. ToF () is interpolated using cosine technique described in [24] and and are using linear interpolation.
Parameters , , and are adjusted using Nelder-Mead direct search (simplex search [25]) which does not require derivatives but only the objective function e.g. remainder of subtraction:
Such approach slightly differs from commonly used norm: instead of analyzing just the remainder we analyze how much of the reduction was obtained relative the norm of the original signal.
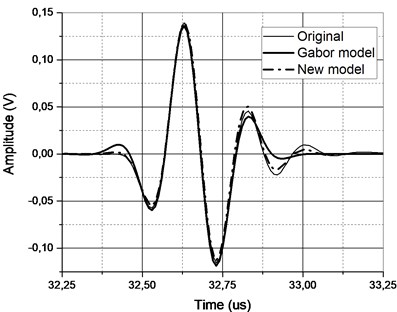
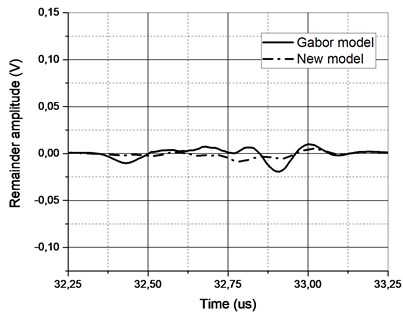
Since both numerator and denominator at Eq. (14) can be attributed to the energy, this parameter was termed remainder energy reduction. The goal of the deconvolution is the complete removal of the reflection from the signal so it is not interfering with remaining reflections. The stronger is the remainder reduction the better is performance of the succeeding deconvolution steps. It might be presumed that remainder energy (or norm) should be a sufficient metric for approximation (so the deconvolution) performance evaluation, but reflection amplitude can be small, so even slight reduction can give acceptable results (refer Fig. 6 for the example of the subtraction remainder representation in time domain).
Fig. 6a) Original A-scan (thin solid line) of the 5 MHz focused transducer signal and its approximation by Gabor (solid) and new function (dash-dot) and b) the corresponding remainders in time domain
a)
b)
Such metric does not represent the actual approximation performance. Ideal approximation should produce very small remainder assuming signal is free from noise (which was accomplished by significant averaging). Low quality of approximation will not be able to offer full stripping of the reflection and the remainder will be high. Then the remainder energy reduction should be the metric to be used and it was further used as approximation performance evaluation criterion. This optimization criterion also satisfies a general deconvolution goal: a reference signal that produces minimal remainder after subtraction.
Initial guess of the , was produced using center of gravity of signal spectrum :
Initial guess of the parameter was produced using half value full width criteria of Hilbert envelope of signal temporal representation:
Initial guess of the parameter was produced using:
Initial guess of the parameter was produced using:
where is the envelope bandwidth:
However, a new problem arises with these algorithms. Depending on initial conditions, the algorithm may remain on the local minimum.
Iterative Gauss Newton optimization method was applied [6] for its high convergence speed. Minimizing the sum of squares of the residual is a common problem. Taking advantage of the echo model, the Gauss Newton iteration formula for estimation of the parameter vector with an initial guess can be written as:
where denotes the Jacobian at initial solution , i.e.:
Hence, the update vector is obtained from the Eq. (27):
This problem can be solved directly. Then we obtain a new update:
and after fixed of Newton steps, the new estimate is obtained:
Performance investigation of the aforementioned algorithm is presented in next section.
5. Experimental results
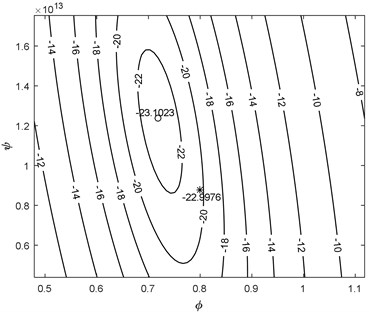
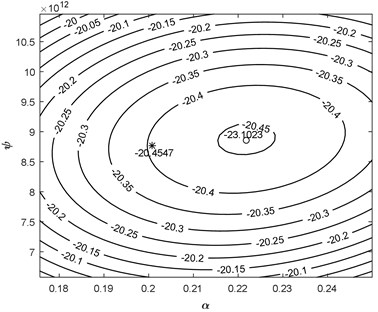
Quality of the convergence was inspected, by artificially varying the model parameters around the final optimization result in order to confirm that global minimum was reached. Refer Fig. 7 for convergence analysis of the parameters , and for focused 5 MHz transducer.
Fig. 72D representation of the remainder energy reduction versus a) φ and ψ and b) α and ψ parameters with simplex (star) and Gauss Newton (circle) optimization for focused 5 MHz transducer
a)
b)
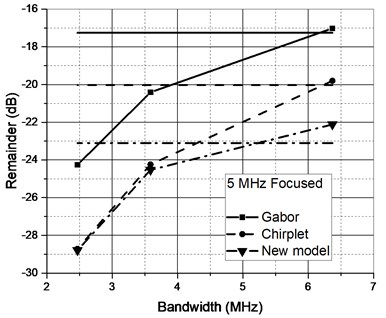
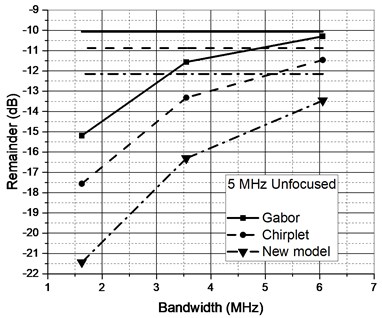
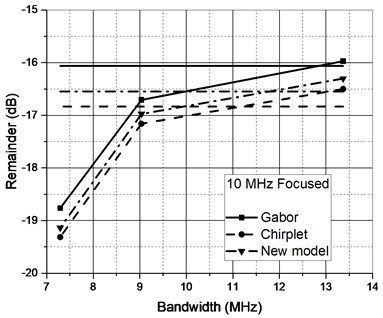
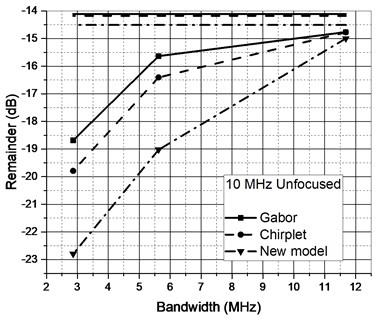
Fig. 8Approximation performance of candidate functions for ultrasonic reflections collected using different transducers when original signal was filtered (horizontal lines – unfiltered case)
a)
b)
c)
d)
Initial guess was out of presented range. Nelder-Mead simplex search produced near optimal result (star) and Gauss Newton optimization (circle) provided fine adjustment. It can be concluded that proposed optimization algorithm locates the global minimum and can be used for the comparison of the model functions.
Further investigation was aimed on deciding whether additional signal filtering is required. Approximation of all four representative signal types was analyzed for the remainder energy reduction in case of raw and filtered signals. Signal cut-off frequencies were chosen basing the –3 dB, –6 dB and –20 dB points established in Section 2. Zero-phase filtering by fourth order Butterworth IIR filter was used. Refer to Fig. 8 for the approximation performance comparison.
It could have been expected that approximation performance will not be high due to the complex nature of the reflections (refer Fig. 9 for remainders comparison of the two most differing reflections, note the new scale compared to Fig. 6). Filtering reduces the complexity of the signal and further improves the SNR. Filters used do not alter the main passband of the signal (–3 dB worst case), albeit improve the approximation performance.
Fig. 9Remainder comparison for a) complex and b) more simple reflections
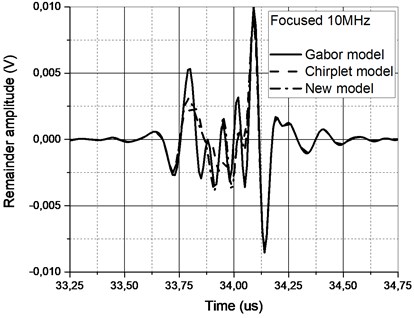
a)
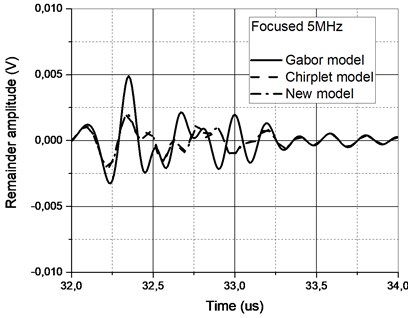
b)
It’s essential to point out that zero-phase filtering has to be used because otherwise signal spectral components are spread in both directions (due to high and low pass filer transition band). It can also be noted that new asymmetrical model function offers the best performance compared to Gabor and Gaussian Chirplet functions.
6. Conclusions
It was demonstrated that simple model functions like Gabor or Gaussian Chirplet demand for envelope asymmetry. New model function, obeying the causality of the ultrasonic signals was proposed. Function possess smooth envelope so can be easily differentiated.
Approximation parameters optimization technique was developed. Technique is based on combination of Nelder-Mead simplex search and iterative Gauss Newton optimization method. Remainder energy reduction of the model function subtraction from the original signal was used as optimization criteria. Grid plots of the remainder reduction versus optimization parameters confirm that technique locates the global maximum.
Four wideband ultrasonic signals were collected as candidates for approximation. Signals were deliberately chosen to significantly deviate from simple model function. Approximation performance investigation was carried out on Gabor, Gaussian Chirplet and newly proposed model functions. It was expected that approximation quality will be low, albeit after some filtering of the signal remainder energy reduction down to 29 dB was achieved.
References
-
Adams R. D., Cawley P. A review of defect types and nondestructive testing techniques for composites and bonded joints. NDT International, Vol. 21, Issue 4, 1988, p. 208-222.
-
Nadeau A., Martin F., Blouin A., Nadeau F., Choquet M., Lord M. Application of laser-ultrasonics to the noncontact, pulse echo measurement of the thickness of micron thin metallic coatings. Review of Progress in Quantitative Nondestructive Evaluation, Vol. 894, 2007, p. 225-230.
-
Hoche S., Hussein M. A., Becker T. Density, ultrasound velocity, acoustic impedance, reflection and absorption coefficient determination of liquids via multiple reflection method. Ultrasonics, Vol. 57, 2015, p. 65-71.
-
Pandey D. K., Pandey S. Ultrasonics: a technique of material characterization. Acoustic Waves, Sciyo, Croatia, 2010, p. 397-430.
-
Ruiz-Reyes N., Vera-Candeas P., Curpian-Alonso J., Cuevas-Martınez J. C., Blanco Claraco J. L. High-resolution pursuit for detecting flaw echoes close to the material surface in ultrasonic NDT. NDT&E International, Vol. 39, Issue 6, 2006, p. 487-492.
-
Bosmann F., Plonka G., Peter T., Nemitz O., Schmitte T. Sparse deconvolution methods for ultrasonic NDT. Journal of Nondestructive Evaluation, Vol. 31, Issue 3, 2012, p. 225-244.
-
Lu Y., Oruklu E., Saniie J. Chirplet signal and empirical mode decompositions of ultrasonic signals for echo detection and estimation. Journal of Signal and Information Processing, Vol. 4, Issue 2, 2013, p. 149-157.
-
Svilainis L., Dumbrava V., Kitov S., Aleksandrovas A., Tervydis P., Liaukonis D. Electronics for ultrasonic imaging system. Elektronika ir Elektrotechnika (Electronics and Electrical Engineering), Vol. 20, Issue 7, 2014, p. 51-56.
-
Rodríguez A., Miralles R., Bosch I., Vergara L. New analysis and extensions of split-spectrum processing algorithms. NDT&E International, Vol. 45, Issue 1, 2012, p. 141-147.
-
Barrodale I., Zala C. A., Chapman N. R. Comparison of the L1 and L2 norms applied to one-at-a-time spike extraction from seismic traces. Geophysics, Vol. 49, Issue 11, 1984, p. 2048-2052.
-
Chen S. S. B., Donoho D. L., Saunders M. A. Atomic decomposition by basis pursuit. SIAM Review, Vol. 43, Issue 1, 2001, p. 129-159.
-
Zhang G. M., Zhang C. Z., Harvey D. M. Sparse signal representation and its applications in ultrasonic NDE. Ultrasonics, Vol. 52, Issue 3, 2012, p. 351-363.
-
Wiener N. The Interpolation, Extrapolation and Smoothing of Stationary Time Series. Report of the Services 19, Research Project DIC-6037 MIT, 1942.
-
Guo J., Xin Y. Reconstructing outside pass-band data to improve time resolution in ultrasonic detection. NDT&E International, Vol. 50, 2012, p. 50-57.
-
Mallat S. G., Zhang Z. Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing, Vol. 41, Issue 12, 1993, p. 3397-3415.
-
Mu Z., Plemmons R. J., Santago P. Iterative ultrasonic signal and image deconvolution for estimation of the complex medium response. International Journal of Imaging Systems and Technology, Vol. 15, Issue 6, 2005, p. 266-277.
-
Demirli R., Saniie J. Asymmetric Gaussian Chirplet model for ultrasonic echo analysis. IEEE International Ultrasonic Symposium Proceedings, 2010, p. 124-128.
-
Kaaresen K. F., Bolviken E. Blind deconvolution of ultrasonic traces accounting for pulse variance. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, Vol. 46, Issue 3, 1999, p. 564-573.
-
Demirli R., Saniie J. Model-based estimation of ultrasonic echoes. Part I: analysis and algorithms. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, Vol. 48, Issue 3, 2001, p. 787-802.
-
Cardoso G., Saniie J. Ultrasonic data compression via parameter estimation. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, Vol. 52, Issue 2, 2005, p. 313-325.
-
Karaboga D., Gorkemli B., Ozturk C., Karaboga N. A comprehensive survey: artificial bee colony (ABC) algorithm and applications. Artificial Intelligence Review, Vol. 42, Issue 1, 2014, p. 21-57.
-
Zhou J., Zhang X., Zhang G., Chen D. Optimization and parameters estimation in ultrasonic echo problems using modified artificial bee colony algorithm. Journal of Bionic Engineering, Vol. 12, 2015, p. 160-169.
-
Lu Y., Demirli R., Cardoso G., Saniie J. A Successive parameter estimation algorithm for chirplet signal decomposition. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, Vol. 53, Issue 11, 2006, p. 2121-2131.
-
Svilainis L., Lukoseviciute K., Dumbrava V., Chaziachmetovas A. Subsample interpolation bias error in time of flight estimation by direct correlation in digital domain. Measurement, Vol. 46, Issue 10, 2013, p. 3950-3958.
-
Kelley C. T. Iterative Methods for Optimization. Society for Industrial and Applied Mathematics. North Carolina, 1999.
