Abstract
The fractional-order Belousov-Zhabotinsky (BZ) reaction with different time scales is investigated in this paper. Based on the stability theory of fractional-order differential equation, the critical condition of Hopf bifurcation with two parameters in fractional-order BZ reaction is discussed. By comparison of the fractional-order and integer-order systems, it is found that they will behave in different stabilities under some parameter intervals, and the parameter intervals may become larger with the variation of fractional order. Furthermore, slow-fast effect is firstly studied in fractional-order BZ reaction with two time scales coupled, and the Fold/Fold type slow-fast oscillation with jumping behavior is found, whose generation mechanism is explained by using the slow-fast dynamical analysis method. The influences of different fractional orders on the slow-fast oscillation behavior as well as the internal mechanism are both analyzed.
1. Introduction
One of the best-studied chemical oscillation systems is the Belousov-Zhabotinsky (BZ) reaction, which was elucidated by 20 chemical equations to explain the reaction mechanism and was simplified to three-variable differential equations [1, 2]. Subsequently, many works about physical and chemical mechanism, numerical simulation and experimental research on BZ reaction appeared abundantly [3-5]. After the 1990s, the slow-fast oscillation was found in many chemical reactions [6, 7], the reason was that the catalyst could make the reaction process involve in different time scales with large gap. One of the classical slow-fast oscillation, i.e. bursting oscillation was observed by Strizhak in the experiment of BZ reaction [8]. However, most of the researches on the slow-fast oscillation in chemical reaction were limited to numerical simulation and experimental investigation.
The better method to qualitatively reveal the bifurcation mechanism of the slow-fast phenomenon should be the slow-fast dynamical analysis method proposed by Rinzel [9]. By use of the method, multiple time-scale systems had been developed in overwhelming growth in last three decades [10-12]. For example, Izhikevich [13] provided all co-dimensional one bifurcation about slow-fast oscillation. Shilnikov [14] had summarized the qualitative methods on Hindmarsh-Rose model, and presented the different bursting oscillations under Hopf bifurcation. Chumakov [15] established a kinetic model of catalytic hydrogen oxidation, and studied the generation mechanism of slow-fast oscillation. Simpson [16] analyzed bursting behavior in a stochastic piecewise system, and discussed the influence of noise on slow-fast oscillation. The bifurcation patterns about neuron system with three time scales were studied by Lu [17]. Li and Bi [18] proposed enveloping slow-fast analysis method to reveal the bursting oscillation mechanism of the system with periodic excitation. Zhang [19] used differential inclusion theory to analyze the bifurcation mechanism of non-smooth systems with multiple time scales.
Actually slow-fast oscillation could be involved not only in the integer-order system but also in the fractional-order system. The reason lies in that fractional calculus would make the dynamical system more complicated, and those slow-fast oscillations have been found in various fields such as chemical, physical, mechanical, electrical, biological, economical and control engineering [20].
In the last three decades, fractional-order dynamical systems had been developed rapidly. Ahmad [21] analyzed the fractional-order Wien-bridge oscillator associated with the periodic oscillations. Ahmed et al. [22] proved the existence and uniqueness of solutions in fractional-order predator-prey system. Wang [23] gave the similarities and differences of the feedbacks between fractional-order and integer-order SDOF linear damped oscillator. Shen et al. [24-29] studied analytically and numerically the primary resonances of van der Pol (VDP) and Duffing oscillators with fractional-order derivative, and investigated the dynamical of linear single degree-of-freedom oscillator with fractional-order derivative. Liu and Duan [30] studied a fractional-order oscillator by Laplace transform and its complex inversion integral formula. Elouahab [31] extended the nonlinear feedback control in fractional-order financial system to eliminate the chaotic behaviors. Many works on stochastic dynamical system with fractional-order derivative had also been done [32-34]. Furthermore, the classical Brusselator with fractional-order derivative was investigated by Gafiychuk [35] and Li [36], in which the stability conditions and limit cycle were discussed.
However, to our best knowledge, the fractional-order BZ reaction is rarely studied, especially when the different time scales is involved. Here we will focus on the fractional-order BZ reaction with two time scales. The paper is organized as follow. In Section 2, the mathematical model of fractional-order BZ reaction is given and the bifurcation condition is discussed. The stabilities of integer-order and fractional-order systems are analyzed in details in Section 3. Then the slow-fast oscillation phenomenon and the corresponding generation mechanism are discussed by use of slow-fast dynamical analysis method in Section 4. At last, the main conclusions of this paper are made.
2. Mathematical model and bifurcation analysis
The photosensitive version of BZ reaction, i.e. Oregonator, was proposed by Seliguchi et al [37], and it was completed by the well-known reaction steps from the FKN mechanism [38], described as:
where is the light-excited molecule of The corresponding mathematical model was given in the form:
where , and represent the concentrations of , , and respectively, and , , and are the dimensionless constants related to the reaction rates. Because these parameters are closely related to the reaction condition such as temperature, pressure, feed rate, etc., the dynamical behaviors of reaction process caused by the parameter variation are very important.
The fractional-order version of BZ reaction could be established as:
in which is the operator of fractional derivative with the order . Obviously, Eq. (1) is a special case of Eq. (2). Here, we adopt Caputo’s definition as:
The equilibria of fractional-order BZ reaction can be obtained as:
where .
The corresponding Jacobian matrix at the equilibrium is:
The stabilities of , and can be determined by the associated characteristic equation:
where:
For convenience, some expressions are defined as follow:
Based on Shengjin’s formulas [39], a method to solve the univariate cubic equation, three real roots can exist in Eq. (3) for . While for , there are a single real root and a pair of conjugate complex roots, shown as:
in which:
The absolute values of arguments of the complex roots are expressed as:
Based on the stability theory of fractional-order differential equation [40], the stability condition for the equilibria of Eq. (2) should be:
In the range of , the stability of Eq. (2) would keep unchanged for , whereas it may be related to the fractional order for . The critical condition for losing stability of Eq. (2) can be expressed as:
where:
Because of , the critical condition Eq. (4) can be .
If we fix the parameters as , and in Eq. (2), three equilibria are calculated and denoted as follow respectively:
is not appropriate in practice and is always unstable, so that only the equilibrium point will be discussed for practical significance. The coefficients of Eq. (3) can be obtained:
and:
The double-parameter bifurcation diagram of Eq. (2) with respect to the parameters and is plotted in Fig. 1(a), where the equilibria are stable in region (I). When the parameters pass across the critical curve into region (II), the equilibria will become unstable, and a stable limit cycle will appear in the system. It is obviously that the parameter range of stable equilibria is bigger than stable limit cycles. However, if , the parameter interval of stable limit cycle is larger than stable equilibria. The phase diagram of the stable limit cycle for and is presented in Fig. 1(b).
Fig. 1The bifurcation diagram and the phase diagram of limit cycle: a) the bifurcation diagram with respect to parameters k and α; b) the phase diagram for the parameters k=0.15 and α=0.995
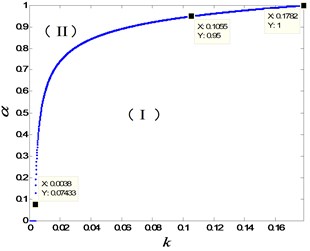
a)
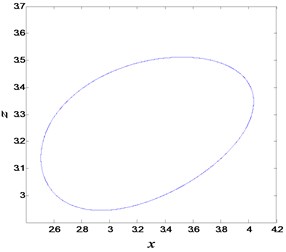
b)
3. Stability analysis of the integer-order and fractional-order system
The parameter is closely related to the stability of the system (2) although it is irrelevant to the equilibrium point of this system. Therefore, the variation of the parameter will result into the change of the dynamical behaviors. The stability of the system for and when will be analyzed in details in the following parts.
Considering , the values of other parameters are the same as those in Section 2. The real and imaginary parts of the eigenvalues of Eq. (2) are plotted in Fig. 2, denoted by the solid line and stars respectively. For , there are two positive and one negative real eigenvalues, so that is unstable. A negative real eigenvalue and two complex conjugate roots are found for . Here we would like to point that the real part of complex conjugate roots undergoes variation with the increase of the parameter . For , the real part of conjugate complex roots is larger than zero, while it is less than zero for . This means that the equilibrium is unstable for and stable for . Therefore, Hopf bifurcation happens at the critical parameter value denoted by point A in Fig. 2(a). On the other hand, the necessary condition of Hopf bifurcation is that a pair of pure imaginary roots appear in the system, which can be obtained by , and . Because there is stable limit cycle when and stable equilibrium for , the Hopf bifurcation at critical point A is subcritical. This means that stable periodic reaction could exist when the reaction rate is small enough, while large will make the stable periodic reaction disappear, and the concentrations , and will approach constants.
For , there are a negative real eigenvalue and a pair of complex conjugate roots , and all the arguments are shown in Fig. 3. The argument of real eigenvalue is always , and the arguments of the complex conjugate roots may vary with the increase of parameter . The equilibria are unstable for because of . And they are locally asymptotical stable for because the stable condition is met. The critical point of losing stability takes place at , which can also be verified by Fig. 1.
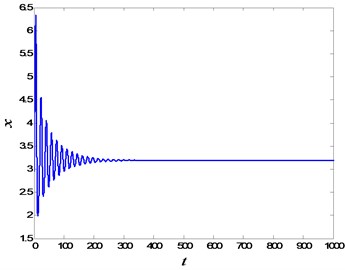
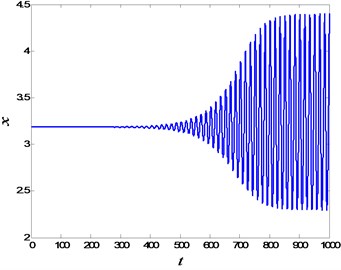
Comparing the abovementioned two situations, it could be found that the stabilities of the fractional-order and integer-order systems are uniform in the most cases. However, there is a parameter interval, (0.1049, 0.1782), in which the stabilities of the two systems are totally different. In this interval, is unstable for , while it is stable for . The numerical simulations of time history for are plotted in Fig. 4, which coincide with the abovementioned theoretical analysis. Furthermore, with the decrease of fractional order , the interval length of different stability may become larger and larger, which can be found from Fig. 1.
Fig. 2The stability of the integer-order system: a) The real and imaginary parts of the eigenvalues of Eq. (2) for α=1; b) The enlarge figure near k= 3.75×10-3
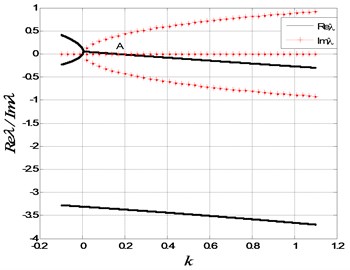
a)
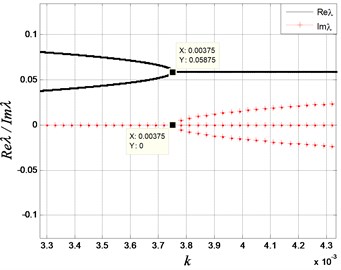
b)
Fig. 3The critical value and the absolute values of eigenvalue’s argument for α= 0.95
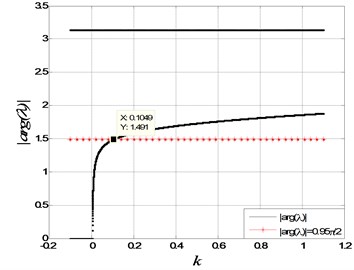
Fig. 4The stability of Eq. (2): a) the time history of the fractional-order system; b) the time history of the integer-order system
a)
b)
4. Fold/Fold slow-fast oscillation and bifurcation mechanism
Considering , Eq. (2) may involve in two time scales, so that the whole system may behave in the typical slow-fast phenomenon. For , the periodic slow-fast oscillation appears in the whole system. The corresponding phase diagram and time history are plotted in Fig. 5. In the periodic process, there are twice instantaneous jumping behaviors, denoted by the arrows in Fig. 5(a). Furthermore, the fast and slow variables present different dynamical features. For the fast variable , the instantaneous jumping behaviors form the spiking state, and the quiet state takes up the most time in the periodic oscillation, which can be found in Fig. 5(b). While the instantaneous jumping phenomenon doesn’t happen in the slow variable , and it will change uniformly, which is presented in Fig. 5(c). Here we would like to point that the periodic oscillation is stable, which is produced by subcritical Hopf bifurcation. The time histories under different initial values can illustrate the stability of the slow-fast periodic oscillation, as shown in Fig. 6.
Fig. 5The periodic slow-fast oscillation for α=0.95
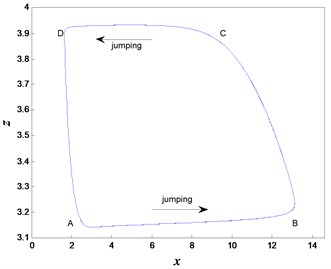
a) The phase diagram
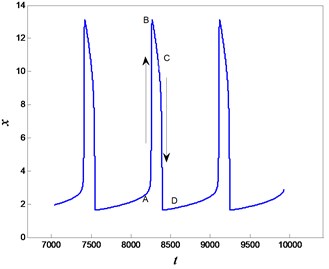
b) The time history for the fast variable
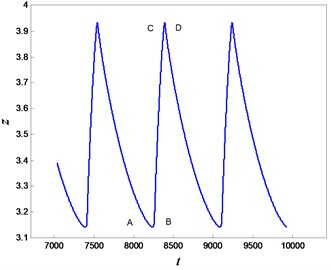
c) The time history for the slow variable
Fig. 6The limit cycle for α=0.95 with different initial values (x*,y*,z*)
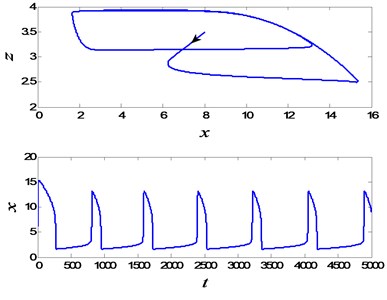
a)
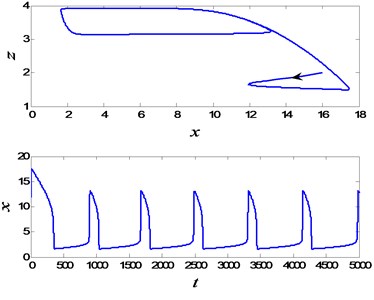
b)
In order to reveal the generation mechanism, we will analyze the system by use of the bifurcation theory. Obviously, the whole system Eq. (2) can be divided into a fast subsystem (FS) and a slow subsystem (SS). The FS is given by the fast variables and , while the SS is modeled by the slow variable . Slow variable is taken as the bifurcation parameter of the fast variables. The FS can be written as:
The equilibria of FS can be determined by:
or
Letting:
one could obtain the extreme points. The extreme points of the equilibrium line is used to analyze the bifurcation of FS. For , and , we can obtain two extreme points, denoted by LP1(2.7425, 3.1569) and LP2(8.6777, 3.8461) respectively. Then the equilibrium line of FS is divided into three branches and plotted in Fig. 7, where the points on the branch (I) and (III) are stable nodes, and the ones on the branch (II) are unstable saddle points. The details can be verified by Fig. 8, where the eigenvalues of the equilibrium curve are presented. Therefore, LP1 and LP2 are the critical points of the Fold bifurcation of FS. Here we would like to point out that the equilibria are either nodes or saddles under the taken parameter condition. The imaginary parts of eigenvalues are always zero, so that the stabilities of FS may keep unchanged with the variation of the fractional order.
Fig. 7Bifurcation diagram of FS
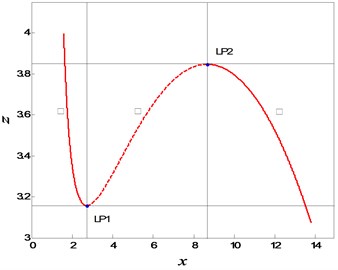
Fig. 8The eigenvalues of FS in Fig. 7
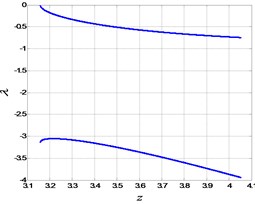
a) The eigenvalues for branch (I)
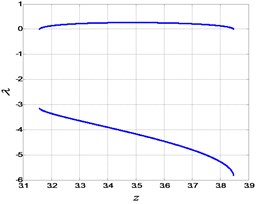
b) The eigenvalues for branch (II)
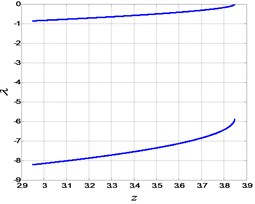
c) The eigenvalues for branch (III)
Because the system possesses fast and slow subsystems, the slow-fast dynamical analysis method is used here. By overlapping the bifurcation diagram of FS with the phase diagram of the whole system, Fig. 9 is obtained, which can be used to explain the generation mechanism of the periodic slow-fast oscillation.
Fig. 9Overlapping of phase diagram of the fractional-order system with bifurcation diagram of FS for α=0.95
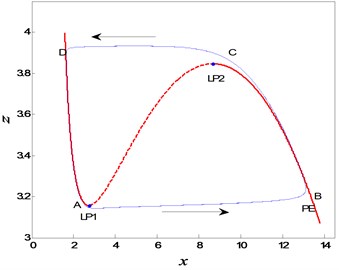
Now we describe the periodic oscillation in details. The trajectory beginning at point D may keep in quiescent state (QS), because the trajectory may move slowly along the stable equilibrium line branch (I) of FS. The QS will be interrupted at point A, where the trajectory moves to the minimal value, i.e. the critical point LP1 of Fold bifurcation of FS. At the same time, the system may be attracted by the stable attractors on branch (III), which results into the jumping phenomenon called as spiking state (SP). When the trajectory jumps to point B, the system response may enter QS again, shown as the slow movement along the stable equilibrium line branch (III). When the system response arrives at the critical point LP2 of FS, the QS terminates and is followed by the SP characterized by jumping to point D because of the attraction from the stable equilibrium line branch (I). The whole procedure forms one period of oscillation. In a word, the twice Fold bifurcations result into twice transitions between the QS and FS, so that the periodic oscillation should belong to Fold/Fold type slow-fast oscillation.
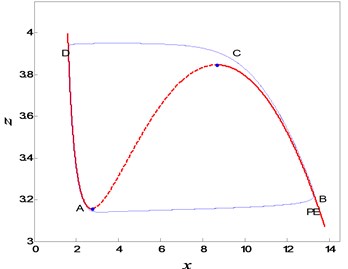
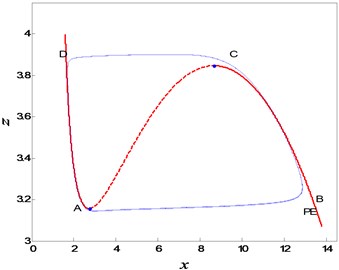
Fig. 10The generation mechanisms of periodic slow-fast oscillation for different fractional orders
a)
b)
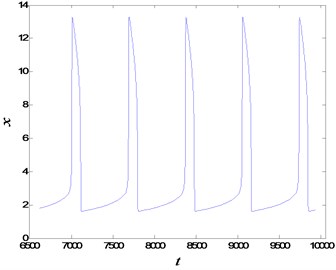
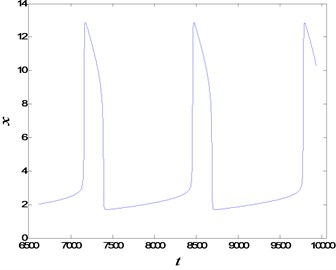
Furthermore, the effect of fractional order on the periodic slow-fast oscillation is compared here. The generation mechanisms for and are shown in Fig. 10. From the figure it could be observed that the generation mechanisms of the periodic oscillation are almost the same with the variation of the fractional order. The primary reason should be that the type of the equilibrium point of the subsystem keeps unchanged with the variation of the fractional order. However, the oscillation period may become much longer with the decrease of fractional order . The differences between the periods of integer-order and fractional-order systems lie in the fact, power law stability [41] is used to define the asymptotical stability of fractional-order system instead of traditional exponential stability. The details associated with the time histories can be found in Fig. 11.
Fig. 11The time histories of periodic slow-fast oscillation for different fractional orders
a)
b)
5. Conclusions
The fractional-order BZ reaction is investigated by use of theoretical analysis and numerical simulation. Based on the stability condition of fractional-order system, the double-parameter bifurcation diagram with respect to fractional order is firstly given, and subcritical Hopf bifurcation is found in fractional-order BZ reaction. By comparing factional-order and integer-order systems, we present the parameter interval about different stability of the two systems, and find that the different features may become more obvious with the increase of fractional order.
Furthermore, the slow-fast oscillation phenomenon is firstly discussed in fractional-order BZ reaction with two time scales coupled. Based on the slow-fast dynamical analysis method, it is found that the fast subsystem possesses twice Fold bifurcations, which leads the system to jump transiently. The switch between different stable equilibrium line branches results into the transition between QS and SP. Accordingly, the slow-fast oscillation belongs to Fold/Fold type. It is also found that the effect of fractional order on trajectory shape and generation mechanism is small, because the type of the equilibrium points of FS keeps unchanged with the variation of the fractional order. However, power law stability in fractional-order system will make the period become longer.
References
-
Field R. J., Koros E., Noyes R. M. Oscillations in chemical systems II Thorough analysis of temporal oscillation in the bromate-cerium-malonic acid system. Journal of the American Chemical Society, Vol. 94, Issue 25, 1972, p. 8649-8664.
-
Field R. J., Noyes R. M. Oscillations in chemical systems. IV. Limit cycle behavior in a model of a real chemical reaction. Journal of Chemical Physics, Vol. 60, Issue 5, 1974, p. 1877-1884.
-
Huh D. S., Choe Y. M., Park D. Y., Park S. H., Zhao Y. S., Kim Y. J., Yamaguchi T. Controlling the Ru-catalyzed Belousov-Zhabotinsky reaction by addition of hydroquinone. Chemical Physics Letters, Vol. 417, Issue 4, 2006, p. 555-560.
-
Rita T., Christopher S., Adamatzky A., Costello B. D. L., Bull L. Dynamic control and information processing in the Belousov-Zhabotinsky reaction using a coevolutionary algorithm. Journal of Chemical Physics, Vol. 129, Issue 18, 2008, p. 184708-1-9.
-
Gyorgyi L., Field R. J. A three-variable model of deterministic chaos in the Belousov-Zhabotinsky reaction. Nature, Vol. 355, Issue 6363, 1992, p. 808-810.
-
Strizhak P. E., Kawczynski A. L. Regularities in complex transient oscillations in the Belousov-Zhabotinsky reaction in batch reactor. Journal of Physical Chemistry, Vol. 99, Issue 27, 1995, p. 10830-10833.
-
Lashina E. A., Chumakova N. A., Chumakov G. A., Boronin A. I. Chaotic dynamics in the three-variable kinetic model of CO oxidation on platinum group metals. Chemical Engineering Journal, Vol. 154, Issue 1, 2009, p. 82-87.
-
Kalishin E. Y., Goncharenko M. M., Strizhak P. E. Periodic, mixed-mode and chaotic Regimes in the Belousov-Zhabotinskii reaction catalyzed by ferroin. Kinetics and Catalysis, Vol. 43, Issue 2, 2002, p. 233-244.
-
Rinzel J. Ordinary and Partial Differential Equations. Springer-Verlag, Berlin, 1985.
-
Valorani M., Goussis D. A. Explicit time-scale splitting algorithm for stiff problems: auto-ignition of gaseous-mixtures behind a steady shock. Journal of Computational Physics, Vol. 169, Issue 1, 2001, p. 44-79.
-
Raghavan R., Ananthakrishna G. Long tailed maps as a representation of mixed mode oscillatory systems. Physica D: Nonlinear Phenomena, Vol. 211, Issue 1, 2005, p. 74-87.
-
Yang S. P., Chen L. Q., Li S. H. Dynamics of Vehicle-Road Coupled System. Springer Berlin Heidelberg, 2015.
-
Izhikevich E. M. Neural excitability, spiking and bursting. International Journal of Bifurcation and Chaos, Vol. 10, Issue 6, 2012, p. 1171-1266.
-
Shilnikov A., Kolomiets M. Methods of the qualitative theory for the Hindmarsh-Rose model: a case study – a tutorial. International Journal of Bifurcation and chaos, Vol. 18, Issue 8, 2008, p. 2141-2168.
-
Chumakov G. A., Chumakova N. A. Relaxation oscillations in a kinetic model of catalytic hydrogen oxidation involving a chase on canards. Chemical Engineering Journal, Vol. 91, Issue 2, 2003, p. 151-158.
-
Simpson D. J. W., Kuske R. Mixed-mode oscillations in a stochastic, piecewise-linear system. Physica D: Nonlinear Phenomena, Vol. 240, Issue 14, 2011, p. 1189-1198.
-
Meng P., Lu Q. S., Wang Q. Y. Dynamical analysis of bursting oscillations in the Chay-Keizer model with three time scales. Science China Technological Sciences, Vol. 54, Issue 8, 2011, p. 2024-2032.
-
Li X. H., Bi Q. S. Bursting oscillation in CO oxidation with small excitation and the enveloping slow-fast analysis method. Chinese Physics B, Vol. 21, Issue 6, 2012, p. 100-106.
-
Zhang Z. D., Bi Q. S. Bifurcation in a piecewise linear circuit with switching boundaries. International Journal of Bifurcation and Chaos, Vol. 22, Issue 2, 2012, p. 240-265.
-
Zhou Y., Ionescu C., Machado J. A. T. Fractional dynamics and its applications. Nonlinear Dynamics, Vol. 80, 2015, p. 1661-1664.
-
Ahmad W., El-khazali R., Elwakill A. S. Fractional-order Wien-bridge oscillator. Electronics Letters, Vol. 37, Issue 18, 2001, p. 1110-1112.
-
Ahmed E., El-Sayed A. M. A., El-Saka H. A. A. Equilibrium points, stability and numerical solutions of fractional-order predator-prey and rabies models. Journal of Mathematical Analysis and Applications, Vol. 325, Issue 1, 2007, p. 542-553.
-
Wang Z. H., Du M. L. Asymptotical behavior of the solution of a SDOF linear fractionally damped vibration system. Shock and Vibration, Vol. 18, Issues 1-2, 2011, p. 257-268.
-
Shen Y. J., Yang S. P., Xing H. J., et al. Primary resonance of Duffing oscillator with fractional-order derivative. Communications in Nonlinear Science and Numerical Simulation, Vol. 17, Issue 7, 2012, p. 3092-3100.
-
Shen Y. J., Yang S. P., Xing H. J., et al. Primary resonance of Duffing oscillator with two kinds of fractional-order derivatives. International Journal of Non-Linear Mechanics, Vol. 47, Issue 9, 2012, p. 975-983.
-
Shen Y. J., Wei P., Yang S. P. Primary resonance of fractional-order van der Pol oscillator. Nonlinear Dynamics, Vol. 77, Issue 4, 2014, p. 1629-1642.
-
Shen Y. J., Yang S. P., Sui C. Y. Analysis on limit cycle of fractional-order van der Pol oscillator. Chaos, Solitons and Fractals, Vol. 67, 2014, p. 94-102.
-
Shen Y. J., Yang S. P., Xing H. J. Dynamical analysis of linear single degree-of-freedom oscillator with fractional-order derivative. Acta Physica Sinica, Vol. 61, Issue 11, 2012, p. 110505.
-
Shen Y. J., Wen S. F., Li X. H., Yang S. P., Xing H. J. Dynamical analysis of fractional-order nonlinear oscillator by incremental harmonic balance method. Nonlinear Dynamics, Vol. 85, Issue 3, 2016, p. 1457-1467.
-
Liu L. L., Duan J. S. A detailed analysis for the fundamental solution of fractional vibration equation. Open Mathematics, Vol. 13, 2015, p. 826-838.
-
Abd-Elouahab M. S., Hamri N. E., Wang J. Chaos control of a fractional-order financial system. Mathematical Problems in Engineering, Vol. 17, Issue 4, 2010, p. 270646-1-18.
-
Huang Z., Jin X. Response and stability of a SDOF strongly nonlinear stochastic system with light damping modeled by a fractional derivative. Journal of Sound and Vibration, Vol. 319, Issue 3, 2009, p. 1121-1135.
-
Chen L., Hu F., Zhu W. Stochastic dynamics and fractional optimal control of quasi integrable Hamiltonian systems with fractional derivative damping. Fractional Calculus and Applied Analysis, Vol. 16, Issue 1, 2013, p. 189-225.
-
Xu Y., Li Y. G., Liu D. A method to stochastic dynamical systems with strong nonlinearity and fractional damping. Nonlinear Dynamics, Vol. 83, Issue 4, 2016, p. 2311-2321.
-
Gafiychuk V., Datsko B. Stability analysis and limit cycle in fractional system with Brusselator nonlinearities. Physics Letters A, Vol. 372, Issue 29, 2008, p. 4902-4904.
-
Zhou T. S., Li C. P. Synchronization in fractional-order differential systems. Physica D: Nonlinear Phenomena, Vol. 212, Issues 1-2, 2005, p. 111-125.
-
Sekiguchi T., Mori Y., Hanazaki I. Photoresponse of the (Ru(bpy)3)2+ / BrO3- / H+ system in a continuous-flow stirred tank reactor. Chemistry Letters, Vol. 8, Issue 1993, 1993, p. 1309-1312.
-
Agladze K., Obata S., Yoshikawa K. Phase-shift as a basis of image processing in oscillating chemical medium. Physica D Nonlinear Phenomena, Vol. 84, Issues 1-2, 1995, p. 238-245.
-
Fan S. J. A new extracting formula and a new distinguishing means on the one variable cubic equation. Natural Science Journal of Hainan Normal College, Vol. 2, Issue 2, 1989, p. 91-98.
-
Tavazoei M. S., Haeri M. Chaotic attractors in incommensurate fractional order systems. Physica D: Nonlinear Phenomena, Vol. 237, Issue 20, 2008, p. 2628-2637.
-
Li Y., Chen Y. Q., Podlubny I., Cao Y. Mittag-Leffler stability of fractional order nonlinear dynamic system. Automatica, Vol. 45, Issue 8, 2009, p. 1965-1969.
Cited by
About this article
The authors are grateful to the support by National Natural Science Foundation of China (Nos. 11302136 and 11672191), Natural Science Foundation of Hebei Province (A2014210062), and the Training Program for Leading Talent in University Innovative Research Team in Hebei Province (LJRC006)
