Abstract
With the continuous development of theories, numerical computations and computational conditions, computational aero-acoustics presents huge advantages when they are used to solve the aerodynamic noise. Under low Mach number, objects with complex geometric profiles were selected as the research objects to research their aerodynamic noises at stationary and motion conditions by means of hybrid flow and sound separation algorithm for aerodynamic noise based on immersed boundary method (IBM). Firstly, the incompressible flow field was solved based on immersed boundary method, in order to obtain the flow field parameters as the input values, and solve the linearized acoustic perturbation compressible equation under non-uniform Cartesian meshes. As a result, the generation and diffusion of acoustic waves can be simulated. The circumferential flow field of two tandem circular cylinders was firstly completed and compared with the published test results to verify its reliability of the method proposed in this paper. And at different observation points, the noise distribution characteristics of two tandem circular cylinders were studied, showing that the noise in the vertical plane was distributed symmetrically and its noise intensity was greater than that in the horizontal plane. Moreover, the effect of different cylindrical diameters on radiation noise distribution was also studied, showing that the larger the cylindrical diameter was, the radiation noise close to the cylinder was smaller. Sound radiation problems of flapping wing motion were further studied by IBM, and this model was featured with obvious directivity in terms of its acoustic radiation, similar to the dipole sound source, and obvious periodicity regarding its acoustic pressure distribution. With good generality and practicability, this method can be also used for solving aerodynamic noise problems of other machines.
1. Introduction
Computational aero-acoustics have been successfully used to solve many aerodynamic noises. For instance, the direct noise algorithms can solve the problem of high-speed jet flow noises [1-4]. Airframe noises should be critically considered when commercial aircrafts were designed [4-8]. Many researchers studied problems of airframe noises with standard profiles and airfoil profiles as the research objects [9-12], commonly by means of acoustic analogy methods or hybrid methods. However, due to its low flow Mach number ( 0.3) and complex geometric profile, etc., landing gear noises [13-16] and flapping wing noises [17-19] haven’t been solved completely. They have low Mach number and complex geometric profile that cause these problems difficult to be realized accurately by the direct noise algorithms. For computational aero-acoustics (CAA), there are following several methods to deal with objects with complex geometric profiles: block-structured mesh method [20], overlapping structured mesh method [21-24], finite volume method [25-27] and immersed boundary method (IBM) [28-31]. The first two methods have limitations in solving aerodynamic noise of moving models with complex geometric profiles, and its computational accuracy is generally low. The finite volume method demands higher accuracy of the computational model, longer computing time and greater computing costs. IBM has been widely used to process problems with complex geometric profiles. With IBM, the solution of a problem with very complex geometric profile can be obtained based on non-uniform Cartesian mesh. As a result, the perfect and efficient difference technique can also be used.
In recent, aero-acoustics problem of complex geometric profiles under low Mach number is proposed to be solved by researchers by means of an algorithm with shape connecting surface and high order immersed boundary method [31]. By hybrid method with hydrodynamic force/acoustic separation [32-34], this method is used to compute aerodynamic noises with low Mach number. Through this method, the flow information can be solved by using incompressible N-S equation (INS), and the acoustic field can be predicted by linearized acoustic perturbation compressible equation (LPCE). This INS/LPCE hybrid technology is a coupling method for directly simulating flow noises. This paper plans to adopt the flow filed solver based on immersed boundary method to solve complex LPCE equations [30, 31]. Luo [35] initially put forward to expand this method to higher order using approaching multinomial. With this method, high order precise Dirichlet boundary conditions and Neumann boundary conditions can be realized on the solid wall surface. Therefore, the dispersion and dissipation which are caused by the boundary condition formula can be reduced obviously, so as to further ensure the precise of acoustic wave emission on the wall. In this paper, this method is applied to computing the aerodynamic noises of stationary objects or moving objects with complex geometric profiles. In this paper, the flow noise of two tandem circular cylinders and flapping wing motion is computed based on immersed boundary method. And the computational result is also verified by the corresponding experiment to present its reliability under the fixed and motion boundary condition.
2. Algorithms
2.1. Governing equation
In this paper, the hybrid method based on hydrodynamic force/acoustic separation [32, 33] is adopted to directly compute aerodynamic noise under low Mach number. With this method, all flow variables can be decomposed into incompressible parts and compressible perturbation parts as follows:
Governing equations for incompressible parts are incompressible N-S equation (INS), which represents flow information. Acoustic pulsation and the other compressible effects can be expressed by perturbation variable; the incompressible N-S equation is written in the following:
After obtaining the incompressible flow solution, acoustic perturbation variables can be obtained by solving linearized acoustic perturbation compressible equation (LPCE) [34]. The vector of LPCE equation set can be written as follows:
where is any additional prescribed acoustic source. The boundary conditions on the solid wall are as follows:
where is the unit wall-normal vector, and the initial conditions are normally and . Furthermore, the perturbed velocity (Eq. (5)) and pressure (Eq. (6)) fields are decoupled from the perturbed density field (Eq. (4)), and if one is not interested in a perturbed density field, this equation does not need to be solved. The left hand sides of LPCE represents the effects of acoustic wave propagation and refraction in the unsteady, inhomogeneous base flows, while the right hand side only contains the acoustic source term. For low-Mach number flows, it is interesting to note that the total change of hydrodynamic pressure is the only source term coming from the incompressible base flow and this is consistent with the analysis of Goldstein [36]. The LPCE have been well validated for fundamental dipole/quadruple flow noise problems [37] and also for the low-Mach number turbulent flow noise problems [34, 38]. Further details regarding the derivation of LPCE can be found in Reference [37].
2.2. Numerical method
Incompressible N-S Eq. (3) is solved by one and one step. The spatial derivatives are obtained by using two order central differences. And the flow items and dissipation items are subject to time integral by means of two-order Adams-Bashforth method and Crank-Nicolson method. Pressure Poisson equation is solved by means of multiple mesh method. LPCE spatial discretization is subject to six-order compact central difference, and time integral is subject to four-order Runge-Kutta. Three-order and four-order boundary schemes are adopted near the immersed solid boundary and the computing domain boundary. Because there is no dissipation error in compact central difference, implicit spatial filtering is adopted to restrain high frequency errors for the purpose of ensuring numerical stability. In this paper, ten-order filtering is adopted in the internal areas, and the filtering near the boundaries reduces to two-order from eight-order successively. Compact central difference and the filtering of implicit spatial can be solved by means of tridiagonal matrix.
2.3. Immersed boundary method
The flow problems which have complex immersed boundaries can be completed by the incompressible N-S equation [30]. Before integral for the governing equation, all the elements inside the object are marked as “body point”, and other points outside the object are marked as “fluid point”. Any “body point” adjacent to fluid point is marked as “image point”, as shown in Fig. 1(a). Wall boundary conditions are realized by setting proper values for the image point. In the method of Mittal [30], an “orthogonal” extends to the immersed boundary from the image point. The probe continues extending to the body reaching the “ghost point”, so as to locate the object point at a middle position between the image point and the ghost point. The value of the image point can be computed through linear interpolation by the values of the boundary point and the ghost point along the orthogonal probe direction. The value of the ghost point is obtained through three-dimensional three-linear interpolation by the surrounding fluid points. This provides the boundary conditions of the immersed boundary with the feature of nominal second order accuracy.
Image point value determines whether the boundary conditions at the object point (BI) is met. In particular, a general variable is used for estimating with -order polynomial near object points :
In the above equation, , , , is an unknown coefficient and is expressed as follows:
Fig. 1Diagram of image elements and boundary conditions
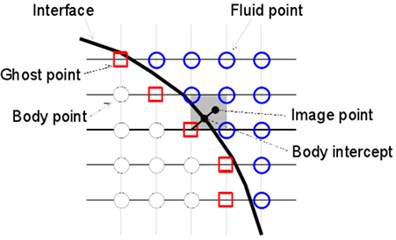
a) Diagram of image elements
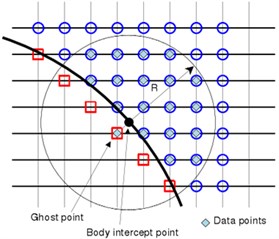
b) Diagram of boundary conditions
The size of coefficients for three-order polynomial (3) is 10 and 20 under two-dimensional and three-dimensional conditions, respectively. To determine these coefficients, the data of the flow field points around the object needs to be obtained. According to the method of Luo [35], the flow field points in the circle or ball (under three-dimensional conditions) with the object point as the center and the radius of can be selected. For data points, coefficient is determined by minimum weighted error estimation:
where is the weight function. According to the previous research experience [35], cosine weight function is used in this paper. To make the least square problem appropriate, radius should be selected in a way which can ensure that there are more data points than coefficients. To find the values of the image point and the object point, the first data point is selected as image points, other (1) data points shall be found in the fluid region (as shown in Fig. 1(b)). The accurate solution of least square problem (Eq. (10)) is as follows:
wherein, the superscript + represents generalized inverse of the matrix, vectorand include coefficient and data respectively; and indicate weight matrix and Vandermonde matrix respectively. It’s noteworthy that represents image points. After solving Eq. (11), coefficient can be written as the linear combination of . According to Eq. (9), coefficient represents the value and derivative value of :
Therefore, for the Dirichlet and Neumann boundary conditions given on object wall, the image point values can be obtained by Eq. (11) and Eq. (12).
Fig. 2Diagram of moving boundary and updated elements
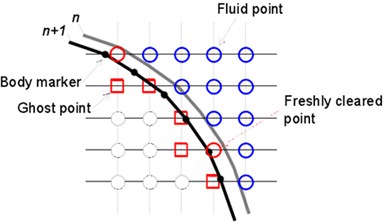
a) Diagram of moving boundary
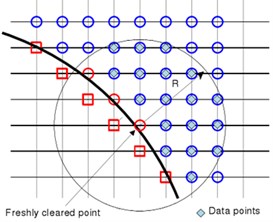
b) Diagram of updated elements
2.4. Disposal for the updated elements
Arbitrary movement of the object is realized by describing the displacement of each node (object identification point) on the triangular mesh of the surface for the immersed object. Disposing the moving object on the fixed mesh will generate “updated elements”, as shown in Fig. 2(a). As the time-dependent variable values of the updated elements don’t need to participate in integral of the governing equation, it is only obtained by the adjacent elements through interpolation [35]. During solving the incompressible flow, the variable values of the new time layer are obtained by iterations of three times of linear interpolation together with the solution of the momentum equation[30]. During solving acoustics, the values of the updated elements are obtained through high order approaching multinomial. The entire process is similar to the disposal for image elements in Section 2.3. However, for the updated element, the center of the data points is updated element , where , , , as shown in Fig. 2(b). To avoid iterations, only the non-updated elements and fluid elements are selected as the data points to minimize Least Squares Error. The coefficient of the approaching multinomial will be obtained by solving Eq. (11), and then the value of the updated element can be directly given by the first coefficient, for instance:
3. Results and discussions
The mentioned methods have successfully been applied to computing noises of flow around a circular cylinder under laminar flow conditions; the effectiveness of the methods has been verified by comparing with the direct computation result based on compressible N-S equation on body-fitted mesh[25]. Sound generation of two tandem circular cylinders is the basic model for researching airframe noises. In this paper, the method is expanded to computing the flow noise problems of two tandem circular cylinders under turbulent flow condition. Meanwhile, to show the solving ability of this method for complex profiles, the aerodynamic noise problems for moving objects with comparatively complex profiles are finally investigated with flapping wing model as the object.
3.1. Turbulent flow noises of two tandem circular cylinders and experimental verification
Two tandem circular cylinders are used as the research object in the paper. Its model is established for numerical simulation, so as to investigate the flow field and flow noise of the fluid when it passes through two tandem circular cylinders. The physical model depended by the numerical simulation can be found in Fig. 3. In the model, the origin of coordinates is located in the center of the upstream cylinder. is an important parameter, wherein is the cylinder diameter and L represents the center distance of two cylinders. The center of the upstream cylinder is at a distance of 5 from the inlet surface, three inlet boundary conditions of speed are given and one outlet boundary condition of pressure is supposed. The circumferential flow field of two circular cylinders is computed by the immersed boundary method and the acoustic field is also computed. To facilitate noise analysis, fast Fourier transform is used to transform fluctuating pressure under time domain into that under frequency domain.
Details of turbulent flow, especially the details of fluctuating turbulent flow, can be captured through finer meshes, which is very important for solving noises. To improve the computational accuracy, the structured mesh is divided to 18 computational zones, as shown in Fig. 4. The encryption was made for the vicinity of cylinder wall, the wake and other regions with relatively complex structures. Considering the computational efficiency brought forward from the fine degree of the meshes, the distance between the wall surface and the first layer of meshes was set as 0.012 mm and then increased externally in proportion. Inflow velocity is 44 m/s and corresponding Reynolds number is 1.66×105. Mach number is 0.128. The size of computation domain is , . Span-wise length is . The total number of non-uniform Cartesian meshes is 768×384×32.
Boundary conditions have to be chosen carefully in order to obtain results which are consistent with physical properties. This paper takes flow velocity as known conditions to compute the turbulent flow noise of two tandem circular cylinders. Therefore, inlet boundary chooses velocity inlet boundary conditions. In the meanwhile, velocity inlet boundary conditions are selected and used for the upper and lower parts of the computational domain. Outlet boundary is pressure outlet boundary. Other boundaries choose wall boundary conditions. The circumferential flow field of two tandem circular cylinders is extremely complex, and the details of the flow should be captured as much as possible during computing noises, so small time steps must be chosen. Meanwhile, considering the restrictions of noise frequency from time step, the interested frequency is less than 5000 Hz, and the time step is 0.0001 s finally.
Fig. 3Physical model of two tandem circular cylinders
Fig. 4Diagram of computational meshes for two tandem circular cylinders
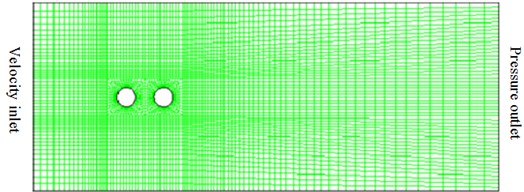
Based on the above computational model, the pressure factor of circumferential flow field for two tandem circular cylinders could be obtained, as shown in Fig. 5. In the figure, BART and QFF represent experiments made by Basic Aerodynamics Research Tunnel and Quiet Flow Facility in NASA center, respectively. As can be seen from Fig. 5(a), the pressure coefficients of upstream and downstream cylinders computed herein show a good consistency with that of the experimental results, but a large deviation between simulation and test is appeared in a few angles, which is within the acceptable range. This indicates the effectiveness of the numerical model in this paper.
The contour of vorticity distribution of two tandem circular cylinders can be found in Fig. 6. It is indicated that the flow process is very complex due to the coupling existing between two tandem circular cylinders. In addition, the separation of flow shear layer is appeared in the upper layer of the upstream cylinder, forming a vortex structure. The upstream cylinder has shown the rolling state of wake before reaching the downstream cylinder, and then its vortex shedding interacts with that of the downstream cylinder. According to Howe’s vortex shedding theory, the aerodynamic noise is caused precisely by vortex shedding.
Fig. 5Comparisons of pressure coefficient for two tandem circular cylinders
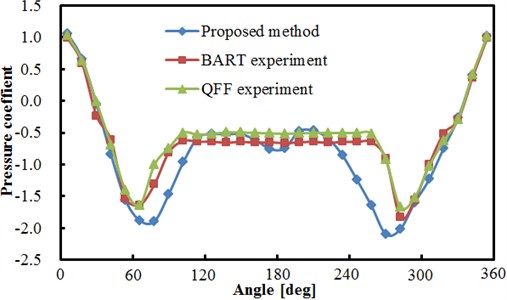
a) Comparisons between experiment and simualtion for upstream cylinder
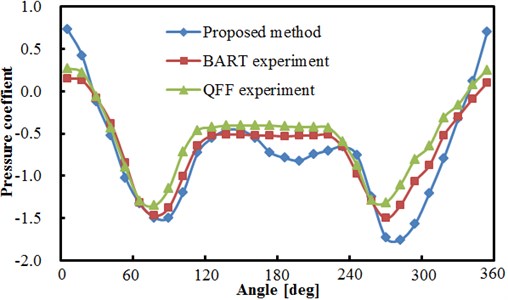
b) Comparisons between experiment and simulation for downstream cylinder
A certain direction is generally shown in noise radiation. To compare the similarities and differences in all directions of perturbation noise of two tandem circular cylinders, eight observation points were defined around the computational model to receive the sound pressure signal, as shown in Fig. 7. In the figure, observation points 1, 4 and 6 are of the same distance to the center of two tandem circular cylinders. Observation points 3, 4, 5 and 6 are in the vertical plane, while observation points 1, 2, 7 and 8 are in a horizontal plane. According to the above computation result and model, the sound field can be further computed in Fluent, whose results are shown in Fig. 8.
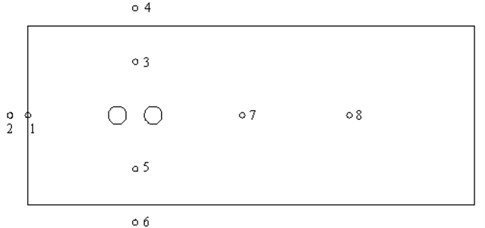
The comparison result of sound pressure levels in observation points 3 and 4 is shown in Fig. 8(a), and two observation points are in the same direction and plane. As can be seen from the figure, the sound pressure level of observation point 3 is significantly greater than that of point 4 over the entire frequency domain, with the biggest difference of nearly 50 dB. The maximum sound pressure level of observation point 3 is 117.2 dB appearing at the frequency near 352 Hz. The maximum sound pressure level of observation point 4 is 100 dB appearing at the frequency near 352 Hz. At the frequency below 2000 Hz, the sound pressure level of observation points 3 and 4 is generally decreased gradually along with the increasing frequency. At the frequency above 2000 Hz, the sound pressure level of observation points 3 and 4 tends to be stabilized generally, which only fluctuates near a certain value. Throughout the entire frequency domain, the valley points of observation point 4 are significantly greater than that of point 3.
Fig. 6Contour of vorticity distribution for two tandem circular cylinders
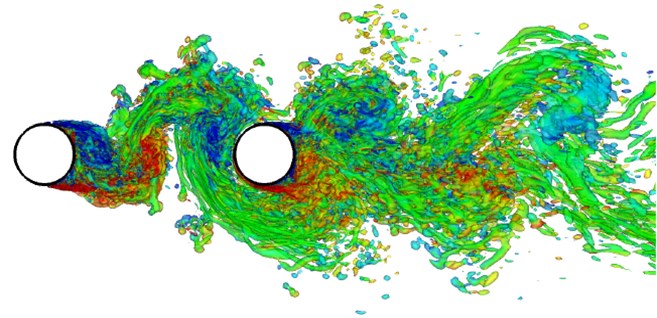
Fig. 7Observation point position of sound pressure signal
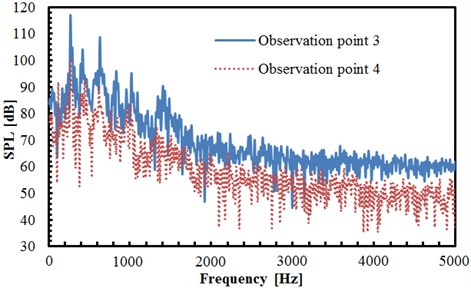
The comparison result of sound pressure levels in observation points 1 and 4 is shown in Fig. 8(b), and two observation points in different planes are of the same distance to the center of two tandem circular cylinders. As can be seen from the figure, the sound pressure level of observation point 4 is significantly greater than that of point 1, with the biggest difference of nearly 40 dB. It is indicated that the radiation noise of two tandem circular cylinders has shown obvious directivity, and the radiation noise in the vertical direction is greater than that in the horizontal direction. The maximum sound pressure levels of observation points 1 and 4 are 88.5 dB and 100 dB, respectively, both appearing at the frequency near 352 Hz. In the entire frequency domain, the valley values of observation point 1 are significantly greater than that of point 4. At the frequency below 1000 Hz, the fluctuations of sound pressure levels are relatively large with evident peaks and valleys. At the frequency below 2000 Hz, the sound pressure level is generally decreased gradually along with the increasing frequency. At the frequency above 2000 Hz, the sound pressure level of two observation points tends to be stabilized generally, which only fluctuates near a certain value. The comparison results in Fig. 8(c) are similar to Fig. 8(b). As can be seen from Fig. 8(b) and Fig. 8(c), the noise intensity in vertical plane is larger than that in horizontal plane.
Fig. 8Comparison of sound pressure levels at observation points
a) Comparison of sound pressure levels in observation points 3 and 4
b) Comparison of sound pressure levels in observation points 1 and 4
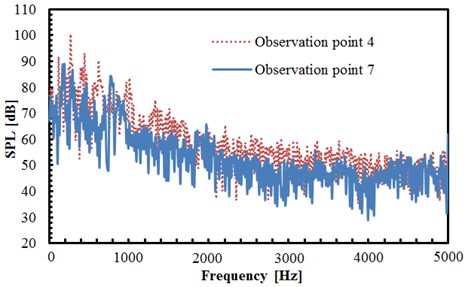
c) Comparison of sound pressure levels in observation points 4 and 7
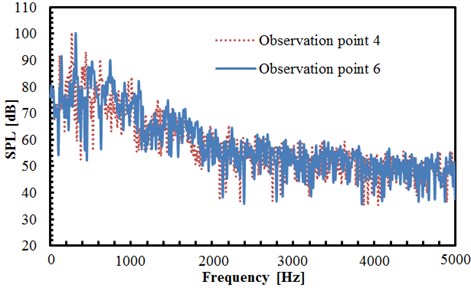
d) Comparison of sound pressure levels in observation points 4 and 6
The comparison result of sound pressure levels in observation points 4 and 6 is shown in Fig. 8(d), and two observation points in the same plane are of the same distance to the center of two tandem circular cylinders. However, the observation point 4 is above the upstream cylinder while point 6 is below the upstream cylinder. As can be seen from the figure, both trends and values of sound pressure levels of two observation points are close, but only peak frequencies of them are slightly different. However, the maximum sound pressure level of both observation points is 100 dB, both appearing at the frequency near 352 Hz. At the frequency below 1000 Hz, the fluctuations of sound pressure levels are relatively large with evident peaks and valleys. At the frequency below 2000 Hz, the sound pressure level is generally decreased gradually along with the increasing frequency. At the frequency above 2000 Hz, the sound pressure level of two observation points tends to be stabilized generally, which only fluctuates near a certain value. In addition, as seen from the analysis of Fig. 8(b) and Fig. 8(c), the acoustic field of two tandem circular cylinders in the vertical plane is distributed symmetrically, and its intensity is larger than that in the horizontal plane.
Two tandem circular cylinders analyzed have the diameter of 10 mm. In the above analysis, the ratio of the cylindrical diameter to the distance between two cylinders would have a serious impact on the flow noise. Therefore, the cylindrical diameter is changed to 20 mm, and the acoustic field distribution around the cylinder is observed. The comparison of sound pressure levels of observation points under cylindrical diameters 10 mm and 20 mm can be found in Fig. 9.
The comparison of radiation noises at the observation point 3 under cylindrical diameters 10 mm and 20 mm can be found in Fig. 9(a). As can be seen from the figure, the sound pressure levels of observation points under the cylindrical diameter of 10 mm is significantly greater than that under the diameter of 20 mm. The maximum sound pressure level under the cylindrical diameter of 10 mm is 118 dB and corresponding frequency is 352 Hz. The maximum sound pressure level under the cylindrical diameter of 20 mm is 116 dB and corresponding frequency is 346 Hz. Therefore, maximum sound pressure levels under different cylindrical diameters only have small differences in the analyzed frequency band and corresponding frequencies approximate 352 Hz. The main reason is that results in low frequencies are mainly affected by boundary conditions for acoustics, and boundary conditions analyzed by different cylindrical diameters are basically the same. Before the frequency point of the maximum sound pressure level, the sound pressure level under the cylindrical diameter of 20 mm is greater than that under the diameter of 10 mm. However, when the frequency exceeds the point of the maximum sound pressure level, the sound pressure level under the cylindrical diameter of 10 mm is greater than that under the diameter of 20 mm, which is only different in individual frequency points. It is mainly because the distance between two circular cylinders is 3.7 and the change of cylindrical diameter greatly changes the distance between two circular cylinders. Under the cylindrical diameter of 20 mm, the distance between two circular cylinders increases to 74 mm. Therefore, the noise between two circular cylinders is relatively low. Moreover, at the frequency below 2000 Hz, the sound pressure level of two cylindrical diameters is generally decreased gradually along with the increasing frequency. But at the frequency above 2000 Hz, the sound pressure level tends to be stabilized near a certain value. The acoustic pressure level under the cylindrical diameter of 20 mm has presented obviously more valley value than that under the diameter of 10 mm.
The comparison of radiation noise at the observation point 4 under cylindrical diameters 10 mm and 20 mm can be found in Fig. 9(b). As can be seen from the figure, the trend of the sound pressure level is not similar to that in Fig. 9(a). The sound pressure level corresponding to different cylindrical diameters is generally of little difference. Only at the frequency of 400 Hz, a larger difference between the two cylindrical diameters is shown. In this case, the sound pressure level under the cylindrical diameter of 20 mm is greater than that under the diameter of 10 mm. Furthermore, obviously more valley values are appeared in the sound pressure level under the cylindrical diameter of 20 mm.
Fig. 9Comparison of sound pressure levels of observation points under different cylindrical diameters
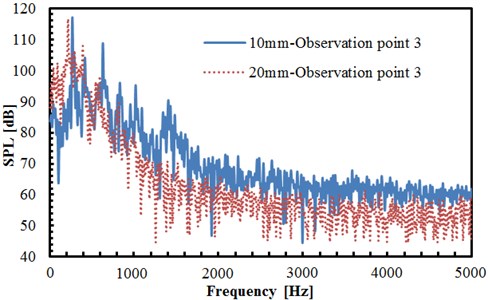
a) Comparison of sound pressure levels of observation point 3 under different cylindrical diameters
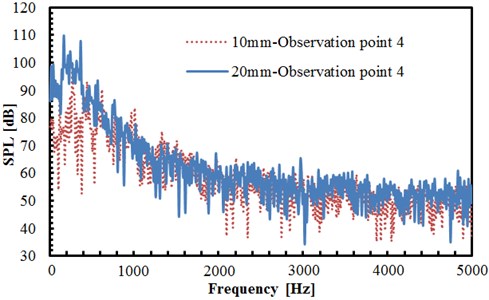
b) Comparison of sound pressure levels of observation point 4 under different cylindrical diameters
3.2. Flow noise induced by flapping wing motion
To verify whether this method is applicable to flow noise problems of moving objects with complex profiles, flapping wing sound generation is computed in this section. Flapping wing is a common structure of insects or micro unmanned aerial vehicle (MAV). Since the micro size of the flapping wing, velocity and Reynolds number are relatively small, and the aerodynamic properties at this time are different from that under the high Reynolds number. Its wing boundary layer becomes sensitive to the changes of the angle. And the separation of its wing boundary layer would be even caused by the minor changes, forming laminar separation bubbles, deteriorating aerodynamic characteristics of wing and appearing increased resistance, significantly dropping the lift to drag ratio and other adverse effects. Along with the flapping of the wing, the surrounding flow field makes unsteady flow, which is therefore difficult to give an accurate explanation by the conventional aerodynamic method. Fig. 10 is the diagram for flapping wing problem. The main body and the wing are standard geometric models, including the wing length of c, the airframe of 0.5 and the wing width of 0.4. The angular velocity of flapping wing movement is described by sine function:
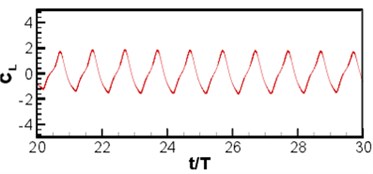
wherein, is the maximum speed at wing-tip, is the distance from the body center to the wing-tip, is the period. Wing length and the maximum speed of wing-tip are selected as the characteristic scales of length and speed. The left and right wings move symmetrically in since function manner. The Reynolds number is 200, Strouhal number is 0.25, Mach number based on wing-tip speed is 0.1. The number of Cartesian grid is 512×512, of which wing length is distinguished by 60 meshes, as shown in Fig. 11(a). See Fig. 11(b) for the contour of vorticity of instantaneous flow field. (as known from the figure, the wingtip has a relatively large speed, showing complementary and symmetrical structure, which is mainly because the wing and airframe are symmetrical and make sinusoidal movement.) Curve of lift coefficient of wing and airframe changing with time is as shown in Fig. 12. (lift coefficient is changed in the similar periodicity to flapping wing movement.) Because of symmetry, the left and right wings share the same lift coefficient. The changing of airframe lift coefficient is caused by the fluid induced by flapping wing movement, (airframe lift coefficient is about one half of the wing, which is consistent with the sizes of airframe and wing).
Fig. 10Diagram of flapping wing motion model
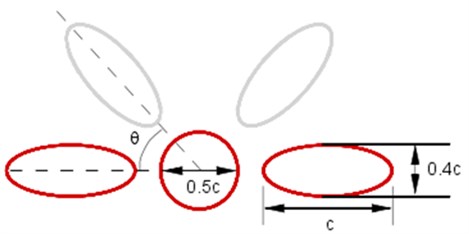
Fig. 11Computational domain of flapping wing movement and contour map of vorticity
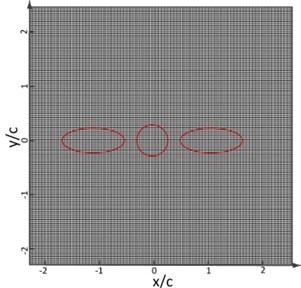
a) Diagram of flapping wing motion model
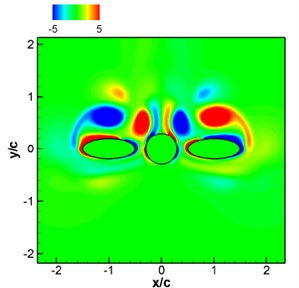
b) Contour map of the instantaneous vorticity
Fig. 12Curve of lift coefficient of flapping wing model with time
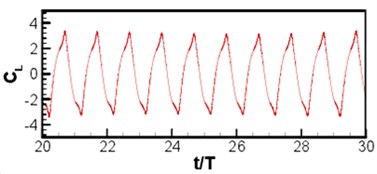
a) Wing of flapping wing model
b) Airframe of flapping wing model
The instantaneous diagram for acoustic field computed by LPCE is as shown in Fig. 13(a). (Because of symmetry, the left and right wings have the same acoustic field.) Based on Strouhal number and Mach number, the wavelength of the main wave is 40. Symmetric flapping wing movement is similar to dipole source, and the sound directivity is shown in Fig. 13(b) where a dipole source can be seen in longitudinal direction. Curves of acoustic pressure changing with time monitored at point (0, 60) and (0, –60)are as shown in Fig. 14. The signal changes periodically, the sound pressure signal presents a periodic change, and sound pressure changes of the symmetrical two observation points are not exactly consistent with a certain phase difference. Although the geometrical shape and movement of the computational model are simple, the computational results show that the algorithm can distinguish the sound generation problems of moving objects very well. To further investigate the sound pressure characteristics of aerodynamic noises, the sound pressure level spectrum of flapping wing motion at different frequencies is shown in Fig. 15. As can be seen from Fig. 15, the interval of peaks in sound pressure level curve is basically remained the same, and the sound pressure level is gradually decreased along with the increasing frequency. The maximum sound pressure level is 26 dB appearing at the frequency near 400 Hz.
Fig. 13Computational results of acoustics for flapping wing model
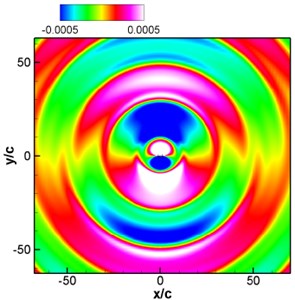
a) Contour of instantaneous sound pressure of the flapping wing model
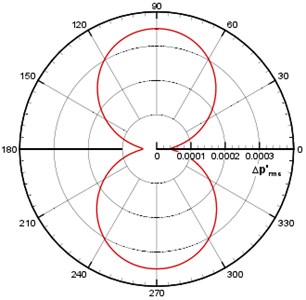
b) Sound directivity pattern ()
Fig. 14Time domain acoustic pressure at observation points of flapping wing model
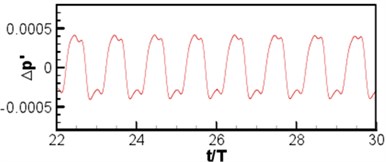
a) (0, 60)
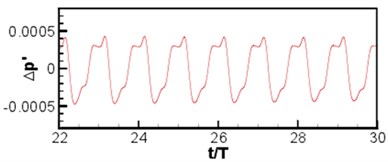
b) (0, –60)
Fig. 15SPL spectrum at different frequencies
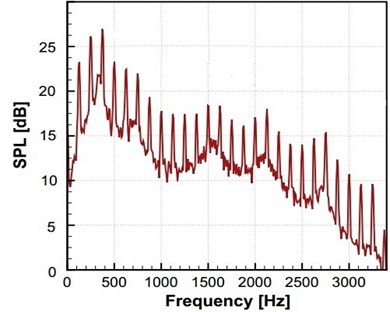
4. Conclusions
In this paper, the aerodynamic noises of objects with complex geometric profiles in stationary or moving statuses under low Mach number are computed. The flow filed and sound generation diffusion of objects with complex profiles under arbitrary motion are computed by means of the hybrid algorithm of incompressible flow field equation based on immersed boundary method and linearized acoustic perturbation compressible equation of acoustic field. The circumferential flow field of two tandem circular cylinders is firstly computed and compared with the published test results to verify its reliability of the method proposed in this paper. And at different observation points, the noise distribution characteristics of two tandem circular cylinders are studied, showing that the noise in the vertical plane was distributed symmetrically and its noise intensity is greater than that in the horizontal plane. Moreover, the effect of different cylindrical diameters on radiation noise distribution is also studied, showing that the larger the cylindrical diameter is, the radiation noise close to the cylinder area is smaller. Sound radiation problems of flapping wing motion are further studied by IBM, and this model is featured with obvious directivity in terms of its acoustic radiation, similar to the dipole sound source, and obvious periodicity regarding its acoustic pressure distribution. With good university and practicability, this method can be used for predicting the noise of low subsonic airframe, fan noise of turbine machinery and electronic equipment as well as the actual application of other aerodynamic noise problems. One of the difficulties for flow field simulation is the computation by Cartesian grid under high Reynolds number conditions, which needs huge computational costs.
References
-
Howe M. S. Contributions to the theory of aerodynamic sound, with application to excess jet noise and the theory of the flute. Journal of Fluid Mechanics, Vol. 71, 1975, p. 625-673.
-
Bechert D., Pfizenmaier E. On the amplification of broad band jet noise by a pure tone excitation, Journal of Sound and Vibration, Vol. 43, 1975, p. 581-587.
-
Tam C. K. W., Viswanathan K., Ahuja K. K. The sources of jet noise: experimental evidence, Journal of Fluid Mechanics, Vol. 615, 2008, p. 253-292.
-
Morris P. J., Farassat F. Acoustic analogy and alternative theories for jet noise prediction. AIAA Journal, Vol. 40, Issue 4, 2002, p. 671-680.
-
Stansfeld S. A., Berglund B., Clark C., et al. Aircraft and road traffic noise and children’s cognition and health: a cross-national study. The Lancet, Vol. 365, Issue 9475, 2005, p. 1942-1949.
-
Hygge S., Evans G. W., Bullinger M. A prospective study of some effects of aircraft noise on cognitive performance in schoolchildren. Psychological Science, Vol. 13, Issue 5, 2002, p. 469-474.
-
Franssen E. A. M., Van Wiechen C., Nagelkerke N. J. D., et al. Aircraft noise around a large international airport and its impact on general health and medication use. Occupational and Environmental Medicine, Vol. 61, Issue 5, 2004, p. 405-413.
-
Haines M. M., Stansfeld S. A., Job R. F. S., et al. A follow-up study of effects of chronic aircraft noise exposure on child stress responses and cognition. International Journal of Epidemiology, Vol. 30, Issue 4, 2001, p. 839-845.
-
Basner M., Samel A., Isermann U. Aircraft noise effects on sleep: Application of the results of a large polysomnographic field studya). The Journal of the Acoustical Society of America, Vol. 119, Issue 5, 2006, p. 2772-2784.
-
Haines M. M., Stansfeld S. A., Head J., et al. Multilevel modelling of aircraft noise on performance tests in schools around Heathrow Airport London. Journal of Epidemiology and Community Health, Vol. 56, Issue 2, 2002, p. 139-144.
-
Aydin Y., Kaltenbach M. Noise perception, heart rate and blood pressure in relation to aircraft noise in the vicinity of the Frankfurt airport. Clinical Research in Cardiology, Vol. 96, Issue 6, 2007, p. 347-358.
-
Lu C., Morrell P. Determination and applications of environmental costs at different sized airports-aircraft noise and engine emissions. Transportation, Vol. 33, Issue 1, 2006, p. 45-61.
-
Thomas F. O., Kozlov A., Corke T. C. Plasma actuators for landing gear noise reduction. AIAA Paper, 2005-3010, 2005.
-
Souliez F. J., Long L. N., Morris P. J., et al. Landing gear aerodynamic noise prediction using unstructured grids. International Journal of Aeroacoustics, Vol. 1, Issue 2, 2002, p. 115-135.
-
Smith M. G., Chow L. C. Validation of a prediction model for aerodynamic noise from aircraft landing gear. AIAA Paper, 2002-2581, 2002.
-
Lockard D. P., Khorrami M. R., Li F. Aeroacoustic analysis of a simplified landing gear. AIAA Paper 2003-3111, 2003.
-
Zdunich P., Bilyk D., Macmaster M., et al. Development and testing of the mentor flapping-wing micro air vehicle. Journal of Aircraft, Vol. 44, Issue 5, 2007, p. 1701-1711.
-
Poelma C., Dickson W. B., Dickinson M. H. Time-resolved reconstruction of the full velocity field around a dynamically-scaled flapping wing. Experiments in Fluids, Vol. 41, Issue 2, 2006, p. 213-225.
-
Bae Y., Moon Y. J. Aerodynamic sound generation of flapping wing. The Journal of the Acoustical Society of America, Vol. 124, Issue 1, 2008, p. 72-81.
-
Manoha E., Guenanff R., Redonnet S., Terracol M. Acoustic scattering from complex geometries. AIAA Paper 2004-2938, 2004.
-
Zahle F., Sørensen N. N., Johansen J. Wind turbine rotor-tower interaction using an incompressible overset grid method. Wind Energy, Vol. 12, Issue 6, 2009, p. 594-619.
-
Tang H. S., Jones S. C., Sotiropoulos F. An overset-grid method for 3D unsteady incompressible flows. Journal of Computational Physics, Vol. 191, Issue 2, 2003, p. 567-600.
-
Fast P., Shelley M. J. A moving overset grid method for interface dynamics applied to non-Newtonian Hele-Shaw flow. Journal of Computational Physics, Vol. 195, Issue 1, 2004, p. 117-142.
-
Chan W. M. Overset grid technology development at NASA Ames Research Center. Computers and Fluids, Vol. 38, Issue 3, 2009, p. 496-503.
-
Rivière B., Wheeler M. F. A Discontinuous Galerkin Method Applied to Nonlinear Parabolic Equations. Discontinuous Galerkin Methods. Springer, Berlin, Heidelberg, 2000, p. 231-244.
-
Schwanenberg D., Köngeter J. A Discontinuous Galerkin Method for the Shallow Water Equations with Source Terms. Discontinuous Galerkin Methods, Springer, Berlin, Heidelberg, 2000, p. 419-424.
-
Castillo P., Cockburn B., Perugia I., et al. An a priori error analysis of the local discontinuous Galerkin method for elliptic problems. SIAM Journal on Numerical Analysis, Vol. 38, Issue 5, 2000, p. 1676-1706.
-
Mittal R., Iaccarino G. Immersed boundary methods. Annual Review of Fluid Mechanics, 2005, 37: 239-261.
-
Lai M. C., Peskin C. S. An immersed boundary method with formal second-order accuracy and reduced numerical viscosity. Journal of Computational Physics, Vol. 160, Issue 2, 2000, p. 705-719.
-
Tseng Y. H., Ferziger J. H. A ghost-cell immersed boundary method for flow in complex geometry. Journal of Computational Physics, Vol. 192, Issue 2, 2003, p. 593-623.
-
Silva A. L. F. L. E., Silveira-Neto A., Damasceno J. J. R. Numerical simulation of two-dimensional flows over a circular cylinder using the immersed boundary method. Journal of Computational Physics, Vol. 189, Issue 2, 2003, p. 351-370.
-
Hardin J. C., Pope D. S. An acoustic/viscous splitting technique for computational aeroacoustics. Theoretical and Computational Fluid Dynamics, Vol. 6, 1994, p. 323-340.
-
Seo J. H., Moon Y. J. The perturbed compressible equations for aeroacoustic noise prediction at low mach numbers. AIAA Journal, Vol. 43, Issue 8, 2005, p. 1716-1724.
-
Seo J. H., Moon Y. J. Linearized perturbed compressible equations for low mach number aeroacoustics. Journal of Computational Physics, Vol. 218, 2006, p. 702-719.
-
Luo H., Mittal R., Zheng X., Bielamowicz S. A., Walsh R. J., Hahn J. K. An immersed-boundary method for flow-structure interaction in biological systems with application to phonation. Journal of Computational Physics, Vol. 227, 2008, p. 9303-9332.
-
Goldstein M. E. A generalized acoustic analogy. Journal of Fluid Mechanics, Vol. 488, 2003, p. 315-333.
-
Seo J. H., Moon Y. J. Aerodynamic noise prediction for long-span bodies. Journal of Sound and Vibration, Vol. 306, Issue 3, 2007, p. 564-579.
-
Moon Y. J., Seo J. H., Bae Y. M., et al. A hybrid prediction method for low-subsonic turbulent flow noise. Computers and Fluids, Vol. 39, Issue 7, 2010, p. 1125-1135.
-
Mittal R., Dong H., Bozkurttas M., Najjar F. M., Vargas A., von Loebbecke A. A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries. Journal of Computational Physics, Vol. 227, 2008, p. 4825-2852.
