Abstract
Dynamic compression test of cement asphalt (CA) mortar specimens, due to water immersion history of 0d, 7d, 14d and 30d, are carried out using a universal electronic test machine, with the strain rates ranging from 1×10-5 s-1 to 1×10-2 s-1. The stress-strain full curves, the compressive strength and the elastic modulus of CA mortar at different strain rates and water immersion durations are analyzed and the effects of strain rates and water immersion duration on these behaviors are studied. Experimental results demonstrate that the compressive strength and elastic modulus increase with the strain rate. In the same strain rate, the compressive strength decreases with the increase of water immersion duration, but the elastic modulus decrease first and then increase with the increase of water immersion duration. The largest reduction of average compressive strength of CA mortar is 46.5 %, and the largest reduction in the average elastic modulus of CA mortar is 47.5 %. A vertical coupling vibration model for a vehicle-railway track-subgrade system was established on the base of wheel-rail coupling dynamics theory and experimental results. The effects of elastic modulus deterioration of CA mortar on the dynamic responses of the vehicle and railway track system were studied. The results show that the reduction of CA mortar has little influence on the dynamic properties of the track and the running stability.
1. Introduction
Cement asphalt (CA) mortar layer, as a filling layer between track slab and concrete supporting layer, functions in supporting, load transfer, adjustment, reduce and isolate vibration, is a key engineering material of slab ballastless track [1-4]. CA mortar is composed of cement, emulsified asphalt, fine aggregates, water and several chemical admixtures. It is an organic-inorganic composite material formed by mechanical mixing. The long-term service performance of CA mortar is very important to the regularity and durability of track, the safety and comfort of vehicle driving. The warpage of the slab was found when the ballastless track under temperature gradient in the actual operation process [4]. If the debonding between CA mortar layer and slab or concrete supporting layer appeared, then the CA mortar layer will be immersed in rain water. Another case, the rain water is pressed into the CA mortar layer by the dynamic load of train from the interface debonding, so the CA mortar layer will be immersed in the rain for a long-term.
As the buffer, damping structure layer of slab track, the CA mortar is mainly under the vertical train load, also in the process of dynamic loading. Therefore, Xie et al. [5], Liu et al. [6] and Wang et al. [7] studied the effects of loading rate on the dynamic mechanical properties of CA mortar, and the results showed that the compressive strength, elasticity modulus and peak strain of CA mortar increases with the loading rate. However, after the CA mortar has been immersed in water for a long time, its dynamic mechanical properties and implications on the behavior of the slab track have not been reported yet. In this paper, the stress-strain full curve of CA mortar was obtained in different water immersion time and strain rates. The influence of water immersion time on the dynamic mechanical properties of CA mortar was studied, and water resistant of CA mortar and its implications on the behavior of the slab track were analyzed.
2. Experiments
2.1. Raw materials
Cement emulsified asphalt mortar special dry ingredients are mainly formed of cement, sand and other additives, and the basic mixture ratio is cement:sand:expanders = 1:2:0.1. The strength grade of Pure Portland cement is 42.5. The 24h volume expansion rate of this cement emulsified asphalt mortar special dry ingredients is 2.1 %, 7d line expansion rate is 0.1 % and the 1 day compressive strength is 6.89 MPa. The asphalt emulsion is the special emulsified asphalt of CA mortar, whose solid mass fraction is 62.1 % [8]. The main properties of emulsified asphalt are listed in Table 1.
Table 1Properties of emulsified asphalts
No. | Item | Unit | Value | |
1 | Engler viscosity (25 °C) | 8.0 | ||
2 | Ratio of screen residue (1.18 mm) | % | 0 | |
3 | Storage stability (1 d, 25 °C | % | 0.3 | |
4 | Storage stability (5 d, 25 °C) | % | 3.2 | |
5 | Residue of mixing with cement | % | 0.3 | |
6 | Evaporated residue | Needle penetration (25 °C, 100 g) | 0.1 mm | 78.5 |
7 | Solubility (trichloroe-thylene) | % | 98.0 | |
8 | Ductility (5 °C) | cm | 26.5 | |
9 | Ductility (15 °C) | cm | 61.2 | |
The J-funnel flow time of fresh CA mortar is 24 s, and the resolution is 0.2 %. The mix proportion of CA mortar is (dry ingredients): (asphalt): (water) = 1100:515:50. Mixing water is the tap water.
2.2. Sample preparation
According to the given mixture ratio of CA mortar, put the emulsified asphalt and water into the pot and stir slowly, add the dry ingredients into the spot slowly in the slowly stirring condition. After the dry ingredients were added, stir rapidly for 3 min and then stir for 1 min. The fluidity, apparent density, gas content and other properties of fresh CA mortar were measured according to the method in paper [9]. The fluidity of CA mortar was 24 s. The apparent density was 1610 kg·m-3 and the gas content was 8.2 %. Then the fresh CA mortar was poured into a cylinder-shape PVC mould with inner diameter of 50 mm and height of 50 mm on the construction site. Top surface of CA mortar block was covered by polyethylene film to prevent the specimens from corrosion and moisture. After the specimens were cured in the standard curing room for 28 days, the water immersion experiment and compression test were done.
2.3. Testing method
In order to simulate the condition of CA mortar layer immersed in water, CA mortar specimens were immersed in the tank after they cured for 28 days, which were shown in Fig. 1. The environment temperature was kept in 20 °C, and the immersion time is 0 day, 7 days, 14 days and 30 days. And then at the regulation age, the mechanical property of CA mortar specimens was tested.
The mechanical property test of CA mortar: uniaxial compressive test of CA mortar specimens in different immersion time was carried out using the WDW series universal electronic test machine according to the method in paper [8], keeping the environment temperature be 20 °C when testing. The universal electronic test machine and its loading principle were shown in Fig. 2. The universal electronic test machine could test the displacement and load value directly. Considering the loading ability of the experimental system, loading rates of 0.03 mm/min, 0.3 mm/min, 3 mm/min and 30 mm/min were set for testing the CA mortar specimens. According to the paper [8], the strain rates were 1×10-5 s-1, 1×10-4 s-1, 1×10-3 s-1 and 1×10-2 s-1, which were obtained according to the size of CA mortar specimens, taking 1×10-5 s-1 as a quasi-static strain rate. Two loading surfaces were coated with French chalk to reduce the surface restraint effect and three samples were used for each test as duplication. If test results are discrete, the number of specimens should be increased in order to ensure the validity of test data. Specimens should be preloaded for three times with loading rate of 0.5 mm/min and strength of 0.05 MPa before the formal loading in order to prevent the error because of the surface unevenness of CA mortar samples.
Fig. 1CA mortar specimens

a) Standard specimen of CA mortar

b) CA mortar immersed in water
Fig. 2The universal electronic test machine and its loading principle

a) Universal electronic test machine
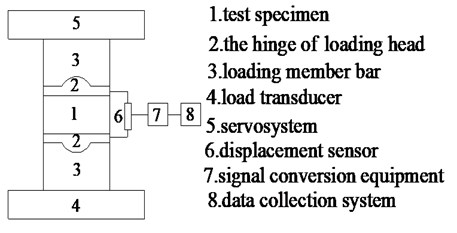
b) The loading principle of universal testing machine
3. Results and discussion
3.1. Stress-strain full curve of CA mortar
The mechanical property of CA mortar was fully reflected by the stress-strain full curve of CA mortar. The testing stress-strain full curves of CA mortar are shown in Fig. 3. Fig. 3(a) shows the stress-strain full curves of CA mortar under different strain rate, which was not immersed in water. As is shown in Fig. 1(a), the stress-strain curves of CA mortar change obviously under different strain rates, and the ultimate compressive strength of CA mortar increases with the strain rate. Fig. 3(b) shows the stress-strain full curves of CA mortar under different water immersion time when the strain rate is 1×10-4 s-1. As shown in Fig. 3(b), the ultimate compressive strength of CA mortar decreases with the increase of water immersion time. The strength of CA mortar decreases slowly when the strength of CA mortar reaches to the peak strength. The existence of asphalt improves the fracture toughness of CA mortar, and the CA mortar has enough bearing capacity even when the strain reaches to 0.1, which indicates that the CA mortar has good toughness and ductility.
Fig. 3Stress-strain full curves of CA mortar
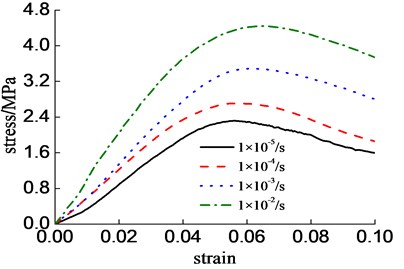
a) Different strain rates
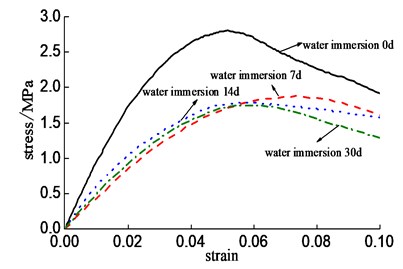
b) Strain rate is 1×10-4 s-1
3.2. Relationship between mechanical property of CA mortar and water immersion time
Compressive strength and elastic modulus are important parameters of the mechanical property of CA mortar. In this paper the compressive strength of CA mortar is the peak stress of the stress-strain full curve, and the elastic modulus use the secant modulus whose compressive strength is 0-1/3 as the elasticity modulus of CA mortar [6], which can be formulated by: . In this formula, is the elasticity modulus of CA mortar, is the 1/3 of ultimate compressive strength. is the initial stress. In this experiment, is 0. is the strain corresponding to . is the initial strain value, which is 0.
The uniaxial dynamic compressive strength and elastic modulus of CA mortar under different water immersion time and strain rates are shown in Table 2.
Table 2Dynamic compressive strengths of CA mortar under different water immersion time
Strain rates/s-1 | Test | Dynamic compressive strength / MPa | Elasticity modulus / MPa | ||||||
0d | 7d | 14d | 30d | 0d | 7d | 14d | 30d | ||
1×10-5 | 1 | 2.31 | 1.56 | 1.34 | 1.20 | 88.8 | 43.4 | 39.4 | 51.4 |
2 | 2.32 | 1.38 | 1.51 | 1.13 | 75.0 | 46.6 | 43.7 | 35.5 | |
3 | 2.20 | 1.51 | 1.44 | 1.34 | 68.5 | 40.2 | 44.9 | 46.3 | |
Average | 2.28 | 1.48 | 1.43 | 1.22 | 77.4 | 43.4 | 42.7 | 44.4 | |
1×10-4 | 1 | 2.80 | 1.88 | 1.79 | 1.76 | 94.4 | 42.8 | 60.2 | 48.7 |
2 | 2.79 | 1.85 | 1.73 | 1.69 | 82.2 | 49.9 | 48.5 | 57.9 | |
3 | 2.79 | 1.89 | 1.84 | 1.71 | 96.9 | 50.8 | 53.0 | 52.6 | |
Average | 2.79 | 1.87 | 1.78 | 1.72 | 91.1 | 47.8 | 53.9 | 53.1 | |
1×10-3 | 1 | 3.42 | 2.89 | 2.78 | 2.74 | 109.1 | 64.1 | 77.2 | 72.9 |
2 | 3.48 | 2.88 | 2.67 | 2.57 | 95.2 | 76.2 | 71.5 | 75.7 | |
3 | 3.37 | 2.90 | 2.75 | 2.77 | 85.1 | 88.6 | 76.4 | 83.8 | |
Average | 3.42 | 2.89 | 2.73 | 2.69 | 96.5 | 76.3 | 75.0 | 77.5 | |
1×10-2 | 1 | 4.45 | 3.88 | 3.83 | 3.79 | 110.9 | 86.8 | 85.6 | 110.9 |
2 | 4.49 | 3.91 | 3.76 | 3.74 | 102.2 | 85.1 | 88.7 | 116.9 | |
3 | 4.43 | 3.96 | 3.77 | 3.78 | 127.7 | 91.9 | 84.3 | 107.8 | |
Average | 4.46 | 3.91 | 3.79 | 3.77 | 113.6 | 87.9 | 86.2 | 111.9 | |
As is shown in Table 2, the ultimate compressive strength and elastic modulus of CA mortar increases with the increase of strain rate under the same water immersion time. The ultimate compressive strength of CA mortar increases with the increase of strain rate, because the damage of CA mortar didn’t develop with the original micro fracture, but with the path of dissipating energy quickly. In the same strain rate, the ultimate compressive strength of CA mortar decreases with the increase of water immersion time. The lower the strain rate is, the more reduction of strength of CA mortar immersed in water. And when the strain rate is 1×10-5 s-1, the average compressive strength of CA mortar decreases from 2.28 MPa to 1.22 MPa, which decreased by 46.5 %, when the water immersion time increase from 0 day to 30 days.
The strength of CA mortar comes from the hydration of cement and demulsification of asphalt emulsion, and the skeleton structure of CA mortar is formed by the asphalt coated hydration products of cement and sand [10]. The strength of CA mortar is provided by the connection between cement hydration products and asphalt or connection between sand and asphalt. The water will invade the phase interface between asphalt and cement or phase interface between asphalt and sand if the CA mortar was immersed in water for a long time, and the phase interface between cement and water, sand and water, asphalt and water were formed, damaging the junction state of original interface and weakening the bonding force. Finally, the strength of CA mortar reduced, and the phenomenon of “softening” of strength of CA mortar occurred.
As is shown in Table 2, the phenomenon of “softening” has effects on the elastic modulus of CA mortar too. The elastic modulus of CA mortar decreases first and then increases with the increasing of water immersion time under the same strain rate. Comparing with the CA mortar without water immersion, when the CA mortar was immersed in water for 14 days, the strain rate range from 1×10-5 s-1 to 1×10-2 s-1, and the reduction of elasticity modulus of CA mortar are 44.8 %, 47.5 %, 22.3 % and 24.1 %. The elasticity modulus of CA mortar increases with the increase of cement hydration products.
The slab track stiffness is constituted by the stiffness of fastener system, slab, CA mortar, subgrade and so on. If the water immersion appears, the mechanical property of CA mortar will be changed to have an adverse effect on the displacement and stress of the track structure. By analyzing the experiment results, the largest reduction in the elasticity modulus of CA mortar is 47.5 %. We should analyze the effects of CA mortar elastic modulus’ damage on the dynamic behavior of slab track.
4. Numerical model and influence analysis
4.1. Vertical vibration model for the coupled vehicle-track-subgrade system
The CA mortar layer under slab affects mainly on the vertical vibration of system, so this paper only considered the vertical vibration of vehicle, track and subgrade. While establishing the dynamic finite element model for the vertically coupled vehicle-slab track-subgrade system in the ANSYS/LSDYNA software, vehicle components are approximately considered as the rigid body. Each component is connected by the elastic or rigid constraints, thus the vehicle is regarded as a multi-rigid-body system. The car body, boggies and wheel sets are simplified as rigid bodies. Each component is connected by the elastic or rigid constraints, thus the vehicle is regarded as a multi-rigid-body system. The car body, bogies and wheel sets are simplified as rigid bodies and take uniform motion along the longitudinal direction of the railway line. The primary and secondary suspensions are simplified as spring-damping, in which the spring is considered as the linear spring and the damping is considered as the viscous damping [11-14].
The slab track was simulated by three-layer point-supported beam model which considered rail, slab and concrete supporting layer. The rail, slab and concrete supporting layer were simulated by Euler beam elements. The fastening systems were simulated by linear spring-damping elements. The CA mortar layer was simulated by linear spring and damping elements to connect the slab and concrete supporting layer. The subgrade was simulated by uniform linear spring and damping elements. The model of the whole system is shown in Fig. 4.
With regard to the half car model, both car body and the bogie have two-degrees-of-freedom, including vertical and pitch, respectively, while the wheel set has only one-degree-of-freedom, namely vertical. So, there are 10-degrees-of-freedom for the half vehicle system. In order to eliminate the boundary effect, 120 track slabs are established in the model (corresponding to a total 603.77 m). The established model in dynamic finite element software ANSYS/LS-DYNA is shown in Fig. 5.
According to the explicit dynamic theory, the explicit central difference method of large general explicit dynamic analysis program LS-DYNA was used to solve the dynamic response equation [15].
Fig. 4Plane model of vehicle-track-subgrade system

Fig. 5Finite element model for the vertically coupled vehicle-slab track subgrade

4.2. Calculation parameters and model validation
The main parameters for the slab track proceed as follows. The rail with the linear density 60 kg/m is applied and simulated by the discretely supported Euler beam. The beam 161 in the finite element model is adopted using dynamic software of ANSYS/LS-DYNA. The vertical stiffness of the fasteners is 50 kN/mm and the vertical damping is 70 kN·s/m. Both the track slab and the concrete underlayer are simulated by the beam 161 in ANSYS software. The size of the slab is 4.962 m×2.4 m×0.19 m, while the width and the thickness of the concrete underlayer is 3.2 m and 0.3 m respectively. In order to calculate facility, the half width of track was considered. The fastener, the CA mortar layer and the subgrade are all considered as the spring-damping element and are simulated by beam161 in ANSYS. The elastic modulus, thickness and damping of CA mortar corresponds to 300 MPa, 50 mm and 34.58 kN·s/m respectively. The vertical stiffness of the subgrade is 120 MPa/m with the vertical damping of 1.0×105 kN·s/m. Only vertical vibration is considered in the model. The parameters for the vehicle system are based on CRH2 EMU (a widely operated Chinese high-speed train). The mass of car body is 39600 kg, the mass of bogie is 3500 kg, the mass of wheel set is 2000 kg. The nod inertia of car body, side-rolling inertia of car body are 1.94×106 kg·m2 and 1.283×105 kg·m2. The nodding inertia of bogie and the side-rolling inertia bogie are 1752 kg·m2 and 2592 kg·m2. The vertical stiffness of primary suspension and secondary suspension are 1.176×106 N/m and 1.89×106 N/m. The vertical damping of primary suspension and secondary suspension are 1.96×104 N·s/m and 4.0×104 N·s/m. The fixed wheel base, central distance of bogies and wheel radius are 2.5 m, 17.5 m and 0.43 m. The high-speed train passes the subgrade section at the speed of 300 km/h.
The wheel-rail contact connects the vehicle to the track system and can be simplified as a Hertz contact. The wheel-rail contact spring is adopted to simulate the coupling between the vehicle and the track in the model. The simplification of the stiffness of the wheel-rail contact will not influence the result of the vibration analysis and nonlinear contact spring will increase the difficulty of the vibration analysis significantly. So, the stiffness of the wheel-rail contact spring is linearized in the model and can be calculated according to the paper [16]. Based on parameters of CRH2 locomotive, the wheel weight of motor car is 70 kN, and the wheel weight of trailer car is 58.5 kN. The calculated equivalent contact stiffness between wheel and rail are 1.193 GN/m of motor car and 1.131 GN/m of trailer car respectively based on the hertz contact theory.
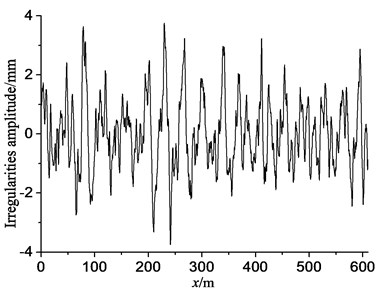
The track irregularity is Germanic low-disturbance spectrum. Fig. 6 shows the time domain random irregularity sample calculated according to Chen and Zhai [17]. ( is the distance apart from the left of model).
Fig. 6Time domain random irregularity sample of the Germanic low-disturbance spectrum
In order to verify the validity of vehicle-track-subgrade vertical vibration model in this paper, the dynamic response was calculated in the condition of CA mortar without deterioration. Fig. 7(a) shows the vertical wheel-rail forces’ time history of back wheel-set, which belongs to back bogie of the fifth motor car. Fig. 7(b) shows the time history of vertical displacement of rail in the middle of the model.
Fig. 7Time history curve of calculation results
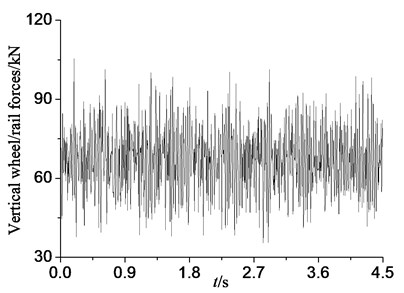
a) Vertical wheel/rail force
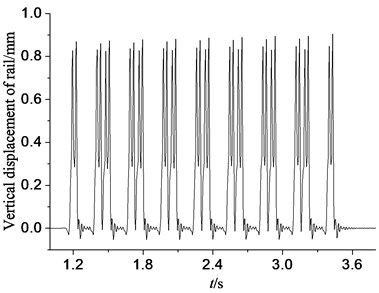
b) Vertical displacement of rail
The maximum dynamic response of simulation calculated in this paper was compared with Liu [18] and the actual measurement of Wuhan-Guangzhou intercity railway [19]. The comparison result is shown in Table 3. As shown in Table 3, the simulation results, each paper and the actual measurement have good consistency, which has verified the reliability of the calculation model.
Table 3Comparison of measured data and calculated results
Index | Vertical wheel/rail force / kN | Displacement of rail/mm | The fulcrum reaction force of rail / kN | Displacement of slab/mm | Dynamic stress of CA mortar layer / kPa |
This paper | 105.2 | 0.905 | 35.435 | 0.267 | 37.483 |
Liu [18] | 94.6 | 0.960 | 38.6 | 0.334 | 35.0 |
Paper [19] | 63.2-102 | 0.78-0.91 | 33-40.5 | 0.18-0.33 | 21.5-54.3 |
4.3. Effects of deterioration of CA mortar on the dynamic properties of track system
Using the calculation model, the dynamic responses of the track system in the conditions of CA mortar without deterioration were analyzed by changing the relevant parameters. According to the experimental results, the elastic modulus of CA mortar is 113.9 MPa, because the maximum age of CA mortar is 58 d. The elastic modulus of CA mortar is 300 MPa according to the paper [8, 9, 16, 20]. And the experiment results show that the largest reduction in the elasticity modulus of CA mortar is 47.5 %. So, assuming that elastic modulus of CA mortar decreased from 300 MPa to 150 MPa.
Changes of the wheel/rail force, vibration acceleration of the car body, vertical displacement of track, reaction force of rail, vertical dynamic compressive stress of CA mortar are small with the elastic modulus deterioration of CA mortar, because the elastic modulus of CA mortar has less effect on the stiffness of the track. Calculation results at the speed of 300 km/h are listed in Table 4.
Table 4Calculation results when the elastic modulus deterioration of CA mortar
Elastic modulus of CA mortar [MPa] | 300 | 270 | 240 | 210 | 180 | 150 | |
Wheel/rail force [kN] | 105.41 | 105.42 | 105.44 | 105.45 | 105.48 | 105.51 | |
Acceleration of car body [m/s2] | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 | 0.21 | |
Vertical displacement [mm] | Rail | 0.905 | 0.9052 | 0.9053 | 0.9054 | 0.9054 | 0.9054 |
Slab | 0.266 | 0.267 | 0.268 | 0.270 | 0.270 | 0.270 | |
Concrete underlayer | 0.263 | 0.263 | 0.263 | 0.264 | 0.264 | 0.265 | |
Reaction force of rail [kN] | 35.48 | 35.47 | 35.45 | 35.42 | 35.37 | 35.31 | |
Compressive stress of CA mortar [kPa] | 37.35 | 36.81 | 36.54 | 36.26 | 35.82 | 35.28 | |
As is shown in Table 4, with the decrease of elastic modulus of CA mortar, the wheel/rail force and vertical displacement of track are increasing. The vibration acceleration of car body keeps the same value when the elastic modulus of CA mortar changes. The reaction force of rail and the vertical dynamic compressive stress of CA mortar decreases with the decrease of elastic modulus of CA mortar. Due to the reduction of elasticity modulus of CA mortar, the stiffness of the track was improved, so the dynamic properties of the track system were improved.
When the elastic modulus of CA mortar is 100 MPa, the whole rigidity of track is 87 kN/mm. And when the elastic modulus of CA mortar increases to 10000 MPa, a growth of 100 times, the whole rigidity of track is 89 kN/mm [20]. The elastic modulus of CA mortar has little influence on the whole rigidity of track, so the deterioration of CA mortar has little influence on the dynamic properties of the vehicle system and track structure.
From the analysis above, the mechanical properties of CA mortar will deteriorate after immersed in water for a long time, but the deterioration has little effect on the dynamic properties of track system and driving stability. Water immersion has influence on the service life of CA mortar, thus the CA mortar should be maintained and repaired in time to improve its durability.
5. Conclusions
The effects of water immersion time on the compressive strength, elastic modulus and stress-strain full curve of CA mortar were studied. A vertical coupling vibration model for vehicle-track-subgrade was established according to the finite element method, the wheel/rail coupling dynamic theory and finite element method. The influence of elastic modulus deterioration of CA mortar on the dynamic properties of the vehicle and track system was researched. The following conclusions can be drawn:
1) The mechanical property of CA mortar is affected obviously by strain rates and water immersion duration.
2) Compressive strength and elastic modulus of CA mortar increase with the strain rate in the same water immersion time. Water immersion will damage the interface of asphalt and the cement hydration products, cause the “softening” of CA mortar, and reduce the strength and elastic modulus of CA mortar. The largest reduction of average compressive strength of CA mortar is 46.5 %, and the largest reduction of the average elastic modulus of CA mortar is 47.5 %.
3) The mechanical properties of CA mortar will deteriorate after immersed in water for a long time, but the deterioration has little effect on the dynamic properties of track system and driving stability.
References
-
Esveld C. Recent development in slab track. European Railway Review, Vol. 9, Issue 2, 2003, p. 81-85.
-
Katsuoshi A. Development of slab tracks for Hokuriku Shinkansen line. Quarterly Report of RTRI, Vol. 42, Issue 1, 2001, p. 35-41.
-
Zeng X. H., Xie Y. J., Deng D. H. Conductivity behavior of fresh CA mortar and its relationship with the fluidity properties. Construction and Building Materials, Vol. 36, 2012, p. 890-894.
-
Xu H., Wang P., Zeng X. H. Present research situation and prospect of CA mortar used in slab ballastless track of high-speed railway. Railway Standard Design, Vol. 11, 2013, p. 1-5, (in Chinese).
-
Xie Y. J., Zeng X. H., Deng D. H., Liu B. J., Zheng K. R. Mechanical characteristics of China railway track system (CRTS) I type slab tracks CA mortar under different strain rates. Journal of Building Materials, Vol. 13, Issue 4, 2010, p. 483-528, (in Chinese).
-
Liu Y. L., Kong X. M., Zhang Y. R., Yan P. Y. Static and dynamic mechanical properties of cement-asphalt composites. Journal of Materials in Civil Engineering, Vol. 10, 2013, p. 1489-1497.
-
Wang F. Z., Liu Z. C., Hu S. G. Influence of loading rate on compressive strength of CA mortar. Journal of Beijing University of Technology, Vol. 34, Issue 10, 2008, p. 1059-1065, (in Chinese).
-
Wang P., Xu H., Chen R., Xu Zeng J. M. X. H. Experimental research on compression properties of cement asphalt mortar due to drying and wetting cycle. Advances in Materials Science and Engineering, Vol. 2014, 2014, p. 769248.
-
Temporary Technology Criterion of Cement and Emulsified Asphalt Mortar in CRTS (China Railway Track System) I Type Slab Track of Passenger Dedicated Railway. 2008, (in Chinese).
-
Wang Q., R. H. A., Yan P. Y. Influence of m(S)/m(C) and sand gradation on compressive strength and fluidity of CA mortar. Journal of Railway Science and Engineering, Vol. 5, Issue 6, 2008, p. 1-5, (in Chinese).
-
Cai C. B., Zhai W. M., Wang K. Y. Calculation and assessment of dynamic performance for slab tracks on Sui-yu Line. China Railway Science, Vol. 27, Issue 4, 2006, p. 17-20, (in Chinese).
-
Zhai W. M. Coupling Dynamics of Vehicle-Track System. 3rd Ed. Science Press, Beijing, Vol. 217, Issue 218, 2007, p. 219-220, (in Chinese).
-
Zhai W. M., Wang K. Y., Cai C. B. Fundamentals of vehicle-track coupled dynamics. Vehicle System Dynamics, Vol. 47, Issue 11, 2009, p. 1349-1376.
-
Wang P., Xu H., Chen R. Effect of cement asphalt mortar debonding on dynamic properties of CRTS II slab ballastless track. Advances in Materials Science and Engineering, Vol. 2014, 2014, p. 193128.
-
Li P., Liu X., Fu X. Analyses of vertical dynamic properties of ballastless track based on LS-DYNA. Proceedings of the 3rd International Conference on Transportation Engineering, Chengdu, China, 2011, p. 1755-1760.
-
Ren J. J., Yang R. S., Wang P., Dai F., Yan X. B. Influence of contact loss underneath concrete underlayer on dynamic performance of prefabricated concrete slab track. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2016.
-
Chen G., Zhai W. M. Numerical simulation of random process about railway track irregularity. Journal of Southwest Jiaotong University, Vol. 2, 1999, p. 138-142, (in Chinese).
-
Liu K. F. Research on Cement Asphalt Mortar Damage and Maintenance Standards for Frame Type of Slab Track. Southwest Jiaotong University, Chengdu, China, 2014, (in Chinese).
-
General Report of the Comprehensive Test of Wuhan Comprehensive Experimental Section for Wuhan-Guangzhou Passenger Dedicated Line. China Academy of Railway Sciences, Beijing, 2009, (in Chinese).
-
Liu X. Y., Zhao P. R., Yang R. S., Wang P. The Design Theory and Method for Ballastless Track on Passenger Dedicated Line. Southwest Jiaotong University Press, 2010, (in Chinese).
Cited by
About this article
This research was supported by the National Science Foundation of China (51425804, U1234201, U1534203), the National Basic Research Program of China (2013CB036202), and the Open Research Fund of MOE Key Laboratory of High-speed Railway Engineering, Southwest Jiaotong University.
