Abstract
For the low accuracy and calculation speed of traditional fault diagnosis methods, the chaos optimization algorithm (COA), quantum particle swarm optimization (QPSO) algorithm and support vector machine (SVM) are introduced into the fault diagnosis to propose a novel fault diagnosis (CQPSMFD) method in this paper. In the proposed CQPSMFD method, the COA is used to initialize the parameters of the QPSO algorithm in order to obtain the CQPSO algorithm with the better convergence speed. Then the CQPSO algorithm is used to optimize the parameters of the SVM model to construct a high-precision SVM model (CQPSM) with the higher accuracy and stronger generalization ability. Next, the CQPSMFD method based on CQPSM method is proposed for motor. Finally, the experiment data from Case Western bearing dataset and actual motor are selected to verify the CQPSMFD method. The results show that the CQPSO algorithm can obtain the optimal parameter combination and the CQPSMFD method can effectively improve the fault diagnosis accuracy and speed.
1. Introduction
Fault is a phenomenon of losing specified function or endangering security of the equipments or systems in the working due to some reasons. It causes the equipments or systems that cannot abnormally operate and reduce their performances. Fault diagnosis is a technology for knowing and mastering the operation state of the equipments or systems, determining whether to be in the abnormal state, early detecting the fault and its reason, and forecasting the fault trend [1]. It plays a very important role to ensure the normal operation of equipments or systems. The fault diagnosis method is used to diagnose, identify and classify the faults in order to prevent emergencies and accidents. Consequently, it is very meaningful to deeply study new fault diagnosis methods for equipments or systems.
Information fusion is a typical problem that involves the integration of multi-source information technologies. A lot of information fusion methods have been developed and proposed in recent years [2]. These information fusion methods are essentially summarized as the stochastic methods and artificial intelligence methods [3-5]. The stochastic methods mainly include Kalman filtering, multi-Bayesian estimation, evidential reasoning and so on. The artificial intelligence methods mainly include fuzzy logic, neural network, rough set, cluster analysis, particle swarm optimization and so on. These information fusion methods play a huge application role in the military, aerospace, energy, metallurgy, petrochemical and other fields.
The SVM is a method based on the statistical learning theory, and it can establish the accurate system model with the good learning ability and generalization ability. Therefore, it is widely applied in the field of information fusion [6, 7]. But the parameters of the SVM play a decisive role to evaluate its learning ability and generalization ability. For the parameter optimization problems of the SVM, many researchers have deeply researched and discussed from the different angle degree in recent years. They proposed a lot of various optimization methods in order to obtain the best parameter combination, such as simulated annealing(SA), grid search, genetic algorithm(GA), differential evolution(DE), particle swarm optimization (PSO), quantum particle swarm optimization(QPSO) algorithm and so on. But these methods have their own defects in the actual application. The SA exists the slow convergence speed and long execution time, its performance is related to the initial parameter value, and the parameters of the SA are sensitive. Grid search method exits the large calculation and long search time. The GA exits the slow convergence speed and premature convergence. The DE is easy to fall into the local optimum value and low convergence accuracy. The PSO algorithm is easy to fall into the local optimum value, and the poor local search ability. The QPSO algorithm is still easy to fall into the local optimum value.
Chaos optimization algorithm(COA) is a population-based stochastic optimization algorithm by using the chaotic map. It is not sensitive to initial value, easy to jump out the local optimum value, and takes on the fast search speed and high calculation accuracy. So the COA is used to improve the QPSO algorithm in order to avoid to fall into local optimum value and premature convergence, improve convergence speed and local search ability. Then the improved QPSO(CQPSO) algorithm is used to optimize the parameters of the SVM to obtain a new information fusion(CQPSM) method, which is applied in the fault diagnosis for proposing a novel fault diagnosis(CQPSMFD) method. Finally, the experiment data from Case Western bearing dataset and actual motor are selected to test and verify the effectiveness of the proposed CQPSMFD method.
2. Related studies
Information fusion is initially known as data fusion. Many researchers proposed a lot of information fusion methods. Sun and Deng [8] proposed scalar weighting information fusion decentralized Kalman filter for discrete time-varying linear stochastic control systems. Xiao et al. [9] proposed a data fusion method based on combining the ANN with wavelet analysis for structural damage detection. Boutros et al. [10] proposed a fuzzy index fusion method to fuse the different indices derived from the same data source of a single sensor. Temko et al. [11] proposed the fusion approach of different information sources with the fuzzy integral for the problem of classifying. Li et al. [12] proposed a fusion method based on the arc sensing and vision sensing information. Jiang et al. [13] proposed a fault diagnosis methodology for rotating machinery by using multisensor information fusion. Anibou et al. [14] proposed a supervised classification algorithm based on discrete wavelet transform and information fusion for the segmentation of the textured images.
Fault diagnosis method began in the early 1970s. It has been receiving more and more attention. A lot of fault diagnosis methods are proposed in the past two decades. Dong et al. [15] proposed a framework based on information fusion by combining different diagnostic tools in a systematic way. Basir and Yuan [16] proposed a fault diagnosis method based on multi-sensor information fusion by using D-S. Peng et al. [17] proposed a vibration fault diagnosis method of hydroelectric unit by using LS-SVM and D-S. Okatan et al. [18] proposed a fault detection approach based on statistics of mathematical expectation of the spectral norm of a normalized innovation matrix for the sensor information fusion Kalman filter. Li et al. [19] proposed an effective autonomous navigation system for the integration of star sensor, infrared horizon sensor, magnetometer, radar altimeter and ultraviolet sensor. Xu et al. [20] proposed a fault diagnosis method based on information fusion method by using interval basic probability assignment in order to deal with the ambiguities in the processes of signal acquisition and fault feature extraction. Moosavian et al. [21] proposed a bearing fault diagnosis method based on vibration analysis by using fisher linear discriminant, K-nearest neighbor and SVM. Li et al. [22] proposed a faulted element identification algorithm based on multisource information fusion for wide-area protection. Dong et al. [23] proposed a modified multi-sensor information fusion method based on combining the improved JDL data fusion model with the hierarchical processing idea. Sarkar et al. [24] proposed a data-driven fault detection method in commercial aircraft gas turbine engines in the framework of multisensor information fusion and symbolic dynamic filtering. Hang et al. [25] proposed a multi-sensors information fusion technology for fault diagnosis of the wind turbine. Xu et al. [26] proposed a sensory information fusion-based diagnostic methodology and framework. Cheng et al. [27] proposed a new gear fault diagnosis method by using multi-sensor information fusion based on combining wavelet correlation feature scale entropy, self-organizing feature map neural network and D-S in strong noise. Xiong et al. [28] proposed an information fusion fault diagnosis method based on a static discounting factor, K-nearest neighbors and dimensionless indicators.
Although these proposed information fusion methods and fault diagnosis methods can better realize different fault diagnosis problems from the different degree of angle in order to obtain good diagnosis results, they exist the defects of low classification accuracy, weak generalization ability and slow convergence speed and so on. So the COA and QPSO algorithm are introduced into the SVM to obtain a new information fusion(CQPSM) method, in order to propose a novel fault diagnosis (CQPSMFD) method for realizing motor fault diagnosis.
3. Basic algorithms and methods
3.1. Quantum particle swarm optimization(QPSO) algorithm
The PSO algorithm is a population-based search algorithm. It consists of a number of individuals, which have one position and one velocity and are denoted as particles. Sun et al. [29] proposed a quantum particle swarm optimization(QPSO) by researching the convergence behavior of the particles from the perspective of quantum mechanics. The QPSO algorithm improved the evolutionary search strategy of the PSO algorithm. This algorithm only needs the velocity vector for finding the global optimal solution. The QPSO algorithm is far superior to the all developed PSO algorithms for the search ability.
In the QPSO algorithm, each particle must converge on the respective random point , , the th dimension of the th particle is described as follow:
A global point is introduced into the PSO algorithm to calculate the next iteration variable of the particle, which is defined as the mean best value of the local optimum position in all particles. The calculated expression is described as follows:
where is the intermediate position in the , is the number of the particles, is dimension value of the particle, is the best position of the particle, is the found optimal solution () of the particle, is the found optimal solution () of all particles, is the related position information. is the contraction or expansion coefficient, , and are the random number in the [0, 1].
In the QPSO algorithm, the particle state is only described by the position vector, and there is only one control parameter . The control of parameter is very important, because the parameter determines the convergence speed of the algorithm. When the QPSO algorithm is used to solve the practical problems, there are several control methods for parameter . The best simple one is that the parameter is set to be a fixed value in the running. But this method is lack of robustness. The other efficient method is linear decreasing strategy that linearly decreases the value of parameter . This method has achieved very good results in the specific practical problems [30]. So the linear decreasing strategy is used to determine the value of parameter in this paper. The expression of the linear decreasing strategy is described:
where is the current number of iterations, 0, 1, 2,…, . is the maximum number of iterations and the value of parameter is from 1 to 0.5.
3.2. Chaos optimization algorithm
Chaos optimization algorithm (COA) [31] is a population-based stochastic optimization algorithm by using the chaotic map. In the COA, it searches all points in turn within changing range of variables, and selects the better point as the current optimum point. Then the current optimum point is regarded as the center, a tiny chaotic disturbance is imposed and a careful search is performed for searching the global optimal point with the high probability. The COA with the refined search space, better search speed and higher search accuracy is selected to optimize QPSO algorithm in this paper. The COA is used to get chaotic variables. So Logistic chaotic model is used to generate the chaotic variable. The mapping equation is given:
where control variable () is the parameter of Logistic. When control variable is 4, Logistic mapping is fully mapped in [0, 1] and it is in the chaotic state. It takes on the traversal between [0, 1], and any state will not repeat. Under Logistic mapping function (the initial condition ), the generated sequences are not periodic and must converge to the specific value outside the given range.
3.3. Support vector machine (SVM)
The SVM is one of the popular tools for supervised machine learning method based on structural risk minimization [32-34]. The characteristic of SVM is to map the original nonlinear data into higher-dimensional feature space. The given training sample is , is the number of samples, the set represents the input vector, indicates the corresponding desired output vector, the input data is mapped into the high dimensional feature space by nonlinear mapping function . The optimal classification hyperplane must meet the following conditions:
where is Omega vector of super plane, is offset quantity. Then the classification decision function is described:
The SVM model is described by the optimization function :
where is slack variable, is offset, is support vector, , is classification parameter for balancing the fitting error and model complexity.
The optimization problem transforms into its dual space. Lagrange function is used to solve. The corresponding optimization problem of the SVM model with Lagrange function is:
where is the Lagrange multiplier, and (1, 2, 3,…, ).
The classification decision function is described:
4. CQPSO and information fusion method
4.1. Chaos quantum particle swarm optimization (CQPSO) algorithm
The QPSO algorithm has better global search ability than the PSO algorithm. But it still exists the premature convergence problem and is easy to fall into the local optimum value. So the determining mechanism of premature convergence is used to avoid the local optimal value:
where is the fitness value of current particle, is the best fitness value of current particle, is the worst fitness value of current particle. With the increasing of iteration, the value of the is decreasing.
The COA method takes on the refined search space, better search speed and higher search accuracy. So a new chaos quantum particle swarm optimization (CQPSO) algorithm based on combining the QPSO algorithm with the chaos method is proposed to improve the convergence speed and convergence precision. In the CQPSO algorithm, Logistic chaotic model is used to generate the chaotic variables, which perturb some particles in order to enhance the local search ability and improve the search accuracy. The flow of the CQPSO algorithm is described:
Step 1. Initialize.
The related parameters and the termination condition are initialized. The is different initial value of the number . The chaotic variables are generated according to Eq. (6).
Step 2. The parameter linearly decreases from 1 to 0.5 with the increasing of iteration.
Step 3. Map into the space domain:
Step 4. Calculate the fitness value.
According to the selected fitness function, the fitness value is calculated. The individual extremum value () and global extremum value () are searched and updated.
Step 5. For each particle, the fitness value of the particle is compared with the fitness value of extremum point, and the population is updated.
Step 6. Determine whether the operation will end. The calculation result meets the end condition, then the operation will end. And the obtained result is output. Otherwise go to step 7.
Step 7. Determine the global extremum value (). If the is not continuously updated, the COA is executed for the best particle in the population. Then go to step 8.
Step 8. The new particle is generated. Go to step 3. to continue the implementation of the CQPSO algorithm.
4.2. Information fusion method
In the SVM, the kernel function is used to map the input into the high-dimensional feature space to find the optimal superplane. So the kernel function must meet the expression:
For fault diagnosis, because the radial basis kernel function takes on better smoothness and analyticity, it is widely applied in the SVM. So the radial basis function is selected as the kernel function of the SVM. Its expression is described as follow:
where is a -dimensional input vector, is the center of the th radial basis function.
In the SVM, the kernel parameter is used to determine the corresponding relation between the mapping function and feature space. It is a very important to select the appropriate value of the for the feature space. The penalty coefficient is used to adjust the proportion of the confidence range and experience risk for obtaining the best learning ability. The penalty coefficient is smaller or larger value, it will cause the poor generalization ability. So it is very critical and difficult to determine the optimal values of the and in the SVM. The COA takes on the advantages of the refined search space, better search speed and higher search accuracy, the QPSO algorithm takes on the global optimization ability. So the COA is used to better initialize the parameters of the QPSO algorithm to propose the CQPSO algorithm. Because the proposed CQPSO algorithm takes on stronger global optimization ability in the feasible solution space, it is used to optimize the and in order to obtain the optimal value combination of the and for constructing a high-precision SVM model (called information fusion (CQPSM)method) with the higher accuracy and stronger generalization ability.
The process of optimizing parameters of the SVM is described in detail: the and of the SVM is selected as combinatorial optimization problem to establish the objective function. Then the CQPSO algorithm is used to search the optimal values of the objective function in order to find out the optimal parameter combination. Firstly, the fitness function is defined:
where is root mean squared error, is the number of training samples, is the actual value of the th sample, is the predicted value of the th sample. The parameter combination with the minimum is selected. The objective function is described:
The function is objective function. The CQPSO algorithm is used to exhaustively search in the domain of and in order to let the objective function to converge to its minimum value. At this time, the values of and are the optimal parameter combination of the SVM.
The flow chart of the CQPSM is shown in Fig. 1.
Fig. 1The flow chart of the CQPSM method
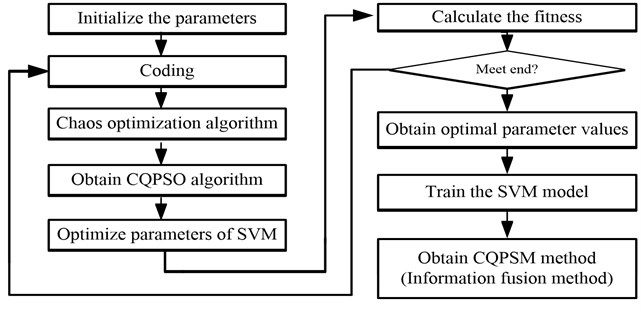
The steps of the CQPSM are described:
Step 1. Initialize.
The initial parameters include population size (), learn factors ( and ), initial control parameter , , and , the maximum iteration (), and the current iteration (). Randomly initialize the velocity and position of each particle in the given range. The position of each particle is defined in .
Step 2. Code for the parameters.
When the CQPSO algorithm is selected to optimize parameters ( and ), each particle is obliged to be replaced by a set of the potential solutions:
Step 3. The following function is selected as the fitness function:
Step 4. Update the local optimal position for each particle and other relevant variables.
Step 5. Update the global optimal position for each particle and other relevant variables.
Step 6. Calculate the value and the random point for each particle.
Step 7. Update the position according to the probability plus and minus for each particle.
Step 8. If the end condition is met, the operation is end and the current best solution is obtained. Otherwise, is executed, return to Step 3 to recalculate until the termination is melted.
Step 9. The optimal parameter combination is entered in the SVM model in order to obtain the information fusion (CQPSM) method.
5. Fault diagnosis method and experiment analysis
5.1. Fault diagnosis method
In order to effectively realize the fault diagnosis and obtain high correctness and speed, the proposed CQPSM method is introduced into fault diagnosis to propose a novel fault diagnosis (CQPSMFD) method in this paper. The process of the proposed CQPSMFD method is illustrated in Fig. 2.
Fig. 2The process of the proposed CQPSMFD method
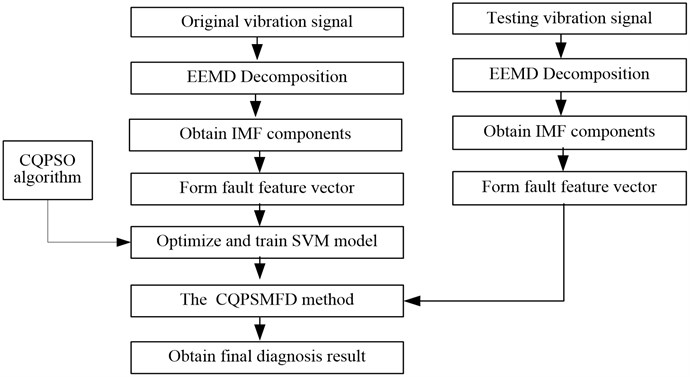
5.2. Experiment and result analysis
The standard vibration data from Case Western bearing dataset and the actual data of motor in industrial production are used to validate the effectiveness of the proposed CQPSMFD method. The experiment environments are Matlab2010b. The initial values of parameters for the CQPSMFD method could be a complicated problem itself, the change of parameters could affect the optimum value. The selected ones are those that gave the best computational results concerning both the quality of the solution and the run time needed to achieve this solution. The initial values are: population size 60, learning factor 2.0, control parameter 1. The max iteration 500.
5.2.1. The standard vibration data for fault diagnosis
The 6205-2RS JEM SKF deep groove ball bearing is employed. In this bearing, the external diameter is 52 mm, the internal diameter is 25 mm, and thickness is 15 mm. These data are acquired with the 12 kHz sampling frequency. The vibration signals are 40 samples for the inner race fault, the outer race fault, rolling element fault and normal state respectively. Firstly, the vibration signals are decomposed by ensemble empirical mode decomposition (EEMD) respectively. The instantaneous amplitude energies of eight IMFs are extracted as the input of the CQPSMFD method. The obtained feature vectors are randomly divided into 30 training samples and 10 testing samples. The feature vectors of bearing are shown in Table 1.
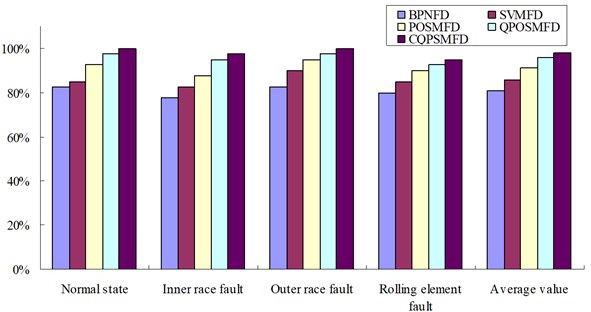
The BPNFD method based on BP neural network, SVMFD based on SVM, POSMFD method based on PSO and SVM, QPOSMFD method based on QPSO and SVM are selected to compare with the CQPSMFD method. The comparison results are shown in Table 2.
As can be seen from Table 2 and Fig. 3, the correctness rates of the proposed CQPSMFD method are 100.0 %, 97.5 %, 100.0 % and 95.0 % for normal state, inner race fault, outer race fault and rolling element fault respectively. For each standard vibration data, the average correctness rate of the proposed CQPSMFD method is 98.125 %. It is best diagnosis result than the BPNFD method, SVMFD method, POSMFD method and QPOSMFD method. The proposed CQPSMFD method can obtain the complete correctness result for the normal signal and outer race fault signal, the correctness rate is 100 %. So the comparison results show that the proposed CQPSMFD method takes on the higher fault pattern recognition accuracy for the standard vibration data in the experiment.
Table 1The feature vectors of bearing
State | Samples | The instantaneous amplitude energy of IMFs | |||||||
Normal state | 1 | 0.512 | 0.705 | 0.104 | 0.251 | 0.388 | 0.072 | 0.007 | 0.003 |
2 | 0.529 | 0.718 | 0.186 | 0.263 | 0.324 | 0.051 | 0.013 | 0.010 | |
3 | 0.536 | 0.726 | 0.241 | 0.278 | 0.285 | 0.043 | 0.024 | 0.013 | |
Inner race fault | 1 | 0.962 | 0.250 | 0.101 | 0.048 | 0.018 | 0.007 | 0.001 | 0.000 |
2 | 0.951 | 0.292 | 0.103 | 0.053 | 0.017 | 0.004 | 0.003 | 0.001 | |
3 | 0.940 | 0.310 | 0.106 | 0.058 | 0.015 | 0.002 | 0.002 | 0.001 | |
Outer race fault | 1 | 0.741 | 0.668 | 0.108 | 0.029 | 0.010 | 0.001 | 0.001 | 0.000 |
2 | 0.709 | 0.703 | 0.105 | 0.024 | 0.007 | 0.003 | 0.000 | 0.000 | |
3 | 0.688 | 0.726 | 0.102 | 0.020 | 0.003 | 0.004 | 0.003 | 0.002 | |
Rolling element fault | 1 | 0.725 | 0.633 | 0.240 | 0.157 | 0.035 | 0.006 | 0.004 | 0.003 |
2 | 0.750 | 0.587 | 0.266 | 0.119 | 0.026 | 0.003 | 0.002 | 0.001 | |
3 | 0.778 | 0.553 | 0.289 | 0.098 | 0.024 | 0.002 | 0.001 | 0.000 | |
Table 2The comparison of fault diagnosis results
State | Diagnosis correctness rate (%) | ||||
BPNFD | SVMFD | POSMFD | QPOSMFD | CQPSMFD | |
Normal state | 82.5 % | 85.0 % | 92.5 % | 97.5 % | 100.0 % |
Inner race fault | 77.5 % | 82.5 % | 87.5 % | 95.0 % | 97.5 % |
Outer race fault | 82.5 % | 90.0 % | 95.0 % | 97.5 % | 100.0 % |
Rolling element fault | 80.0 % | 85.0 % | 90.0 % | 92.5 % | 95.0 % |
Average value | 80.625 % | 85.625 % | 91.25 % | 95.625 % | 98.125 % |
Fig. 3The correct rate comparison result for standard vibration data
5.2.2. The actual data of motor for fault diagnosis
The mechanical fault of motor rotor in industrial production is selected as the actual research object. The type of motor is Y132M-4 and rated speed is 1450 r/min in this paper. The actual vibration signals on the horizontal and vertical directions are collected by using eddy-current sensor. The main faults of motor rotor include the rotor unbalance, rotor misalignment, oil whirl, rotation detachment, surge, losing bearing house and so on. Due to the limited page, the normal state, rotor unbalance and oil whirl are only considered. 0 represents the normal state, 1 represents the rotor unbalance state and 2 represents oil whirl state.
The experiment steps of CQPSMFD method for actual motor are described as follows.
Step 1. Obtain the training and testing date.
In this paper, we select 300 samples. 250 samples are randomly selected as the training samples, the rest (50) is regarded as the testing samples. The describing of these samples is shown in Table 3.
Table 3The describing of these samples
Data type | 0 | 1 | 2 |
Training samples | 50 | 108 | 92 |
Testing samples | 8 | 23 | 19 |
Total samples | 58 | 131 | 111 |
Step 2. Data preprocessing.
Firstly, the mapminmax normalized function in Matlab2010 is used to process the data to the interval of [0, 1]. Rough set is a mathematical method that can be employed to deal with the data with the imprecision, incompletion, vagueness, and uncertainty. It can discover implicit knowledge and reveal potential rules by analyzing and dealing with all kinds of imprecise, incomplete, and disaccord information. So the rough set is used to realize the reduction in order to delete the redundancy attributes and obtain the minimum rule set with the greatest degree.
Step 3. Optimize the parameters of the SVM.
The CQPSO algorithm is used to optimize the and of the SVM in order to obtain the best parameter combination. The optimal values are obtained: 0.024, 0.994.
Step 4. Obtain the CQPSM method.
The obtained parameter values are entered in the SVM model, and the training samples are used to continuously train the SVM for obtaining the optimal SVM (CQPSM).
Step 5. Obtain the CQPSMFD method.
The CQPSM method is applied in fault diagnosis to propose a novel fault diagnosis (CQPSMFD) method.
Step 6. Output diagnosis result.
The testing samples are used to test the effectiveness of the CQPSMFD method. The diagnosis results are obtained in Table 4.
Table 4The diagnosis results of CQPSMFD method
Motor state | Testing data | Testing result | Diagnosis result | Correct rate |
Normal state | 8 | 8 | 0 | 100 % |
Rotor unbalance | 23 | 22 | 1 | 95.7 % |
Oil whirl fault | 19 | 18 | 2 | 94.7 % |
Average value | 96.8 % |
As can be seen from Table 4, for 50 testing samples, the proposed CQPSMFD method can better diagnose the normal state, rotor unbalance and oil whirl fault of motor. For the normal state, the proposed CQPSMFD method can obtain 100 % correct rate. For the rotor unbalance fault and oil whirl fault, the proposed CQPSMFD method can obtain 95.7 % and 94.7 % correct rate, respectively. For the motor fault, the proposed CQPSMFD method can obtain 96.8 % mean correct rate in the testing samples. So the experiment results show that the proposed CQPSMFD method has the higher diagnosis accuracy.
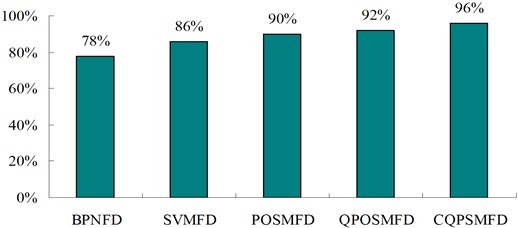
In order to further verify the effectiveness of the proposed CQPSMFD method, the BPNFD method based on BP neural network, SVMFD method based on SVM model, POSMFD method on PSO algorithm and SVM and QPOSMFD method on QPSO and SVM are used to compare with the proposed CQPSMFD method. The initial values of parameters of these methods are obtained by using the experiment. The results of fault diagnosis are shown in Table 5.
As can be seen from Table 5 and Fig. 4, for the given 50 testing samples, the fault diagnosis correct rate of the BPNFD method is lowest, its correct rate is only 78 %. The fault diagnosis correct rate of the SVMFD method is 86 %, and fault diagnosis correct rate of the POSMFD method is 90 %. The fault diagnosis correct rate of the QPOSMFD method is 92 %, and fault diagnosis correct rate of the CQPSMFD method is 96 %. Obviously, the proposed CQPSMFD method can obtain the best fault diagnosis correct rate than the BPNFD method, SVMFD method, POSMFD method and QPOSMFD method. So the experiment results show that the proposed CQPSMFD method can obtain the high fault diagnosis correct rate, and takes on strong robustness.
Table 5The comparison of diagnosis results
Diagnosis method | Testing samples | Testing result | Correct rate |
BPNFD | 50 | 39 | 78 % |
SVMFD | 50 | 43 | 86 % |
POSMFD | 50 | 45 | 90 % |
QPOSMFD | 50 | 46 | 92 % |
CQPSMFD | 50 | 48 | 96 % |
Fig. 4The correct rate comparison of several methods
6. Conclusions
Fault diagnosis is a technology for knowing and mastering the operation state of the equipment or systems, determining whether to be in the abnormal state, early detecting the fault and its reason, and forecasting the fault trend. Information fusion involves the integration of multi-source information technologies. In this paper, in order to improve the low correctness rate of traditional fault diagnosis methods, the COA and QPSO algorithm are introduced into the SVM to optimize the parameters of SVM and obtain a new information fusion (CQPSM) method. The COA with the refined search space, better search speed and higher search accuracy is used to better initialize the QPSO algorithm to obtain the CQPSO algorithm. The CQPSO algorithm with the better global optimization performance is used to optimize the parameters of the SVM in order to propose the CQPSM method with the higher accuracy generalization ability. The CQPSM method is applied in fault diagnosis in order to propose a novel fault diagnosis (CQPSMFD) method. The experiment data from Case Western bearing dataset and actual motor are used to verify the effectiveness of the proposed CQPSMFD method. The mean correctness rates of the proposed CQPSMFD method are 98.125 % for motor bearing and 96.8 % for actual motor rotor in industrial production, respectively. The experiment results show that the proposed CQPSMFD method can obtain the high correct rate and high robustness. The CQPSMFD method can better meet the requirements of the fault diagnosis.
References
-
Nandi S., Toliyat H. A., Li X. Condition monitoring and fault diagnosis of electrical motors-a review. IEEE Transactions on Energy Conversion, Vol. 20, Issue 4, 2005, p. 719-729.
-
Twycross J., Aickelin U. Information fusion in the immune system. Information Fusion, Vol. 11, Issue 1, 2010, p. 35-44.
-
Gu B., Sun X. M., Sheng V. S. Structural Minimax Probability Machine. IEEE Transactions on Neural Networks and Learning Systems, 2016
-
Bahador K., Alaa K., Fakhreddine O. K., Saiedeh N. R. Multisensor data fusion: a review of the state-of-the-art. Information Fusion, Vol. 14, Issue 1, 2013, p. 28-44.
-
Zheng Y. H., Jeon B., Xu D. H., Wu Q. M. J., Zhang H. Image segmentation by generalized hierarchical fuzzy C-means algorithm. Journal of Intelligent and Fuzzy Systems, Vol. 28, Issue 2, 2015, p. 961-973.
-
Wen X. Z., Shao L., Xue Y., Fang W. A rapid learning algorithm for vehicle classification. Information Sciences, Vol. 295, Issue 1, 2015, p. 395-406.
-
Gu B., Sheng V. S. A robust regularization path algorithm for ν-support vector classification. IEEE Transactions on Neural Networks and Learning Systems, 2016
-
Sun S. L., Deng Z. L. Multi-sensor information fusion Kalman filter weighted by scalars for systems with colored measurement noises. Journal of Dynamic Systems, Measurement and Control, Transactions of the ASME, Vol. 127, Issue 4, 2005, p. 663-667.
-
Xiao C., Qu W. L., Tan D. M. An application of data fusion technology in structural health monitoring and damage identification. Proceedings of SPIE, Smart Structures and Materials 2005: Smart Sensor Technology and Measurement Systems, 2005, p. 451-461.
-
Boutros T., Liang M. Mechanical fault detection using fuzzy index fusion. International Journal of Machine Tools and Manufacture, Vol. 47, 2007, p. 1702-1714.
-
Temko A., Macho D., Nadeu C. Fuzzy integral based information fusion for classification of highly confusable non-speech sounds. Pattern Recognition, Vol. 41, Issue 5, 2008, p. 1831-1840.
-
Li W. H., Gao K., Wu J., Hu T., Wang J. Y. SVM-based information fusion for weld deviation extraction and weld groove state identification in rotating arc narrow gap MAG welding. International Journal of Advanced Manufacturing Technology, Vol. 74, Issues 9-12, 2014, p. 1355-1364.
-
Jiang L. L., Yin H. K., Li X. J., Tang S. W. Fault diagnosis of rotating machinery based on multisensor information fusion using SVM and time-domain features. Shock and Vibration, Vol. 2014, 2014.
-
Anibou C., Saidi M. N., Aboutajdine D. Classification of textured images based on discrete wavelet transform and information fusion. Journal of Information Processing Systems, Vol. 11, Issue 3, 2015, p. 421-437.
-
Dong M., Zhang Y., Yang L., Judd M. D. Fault diagnosis model for power transformers based on information fusion. Measurement Science and Technology, Vol. 16, Issue 7, 2005, p. 1517-1524.
-
Basir O., Yuan X. H. Engine fault diagnosis based on multi-sensor information fusion using Dempster-Shafer evidence theory. Information Fusion, Vol. 8, Issue 4, 2007, p. 379-386.
-
Peng W. J., Luo X. Q., Guo P. C., Lu P. Vibration fault diagnosis of hydroelectric unit based on LS-SVM and information fusion technology. Proceedings of the Chinese Society of Electrical Engineering, Vol. 27, Issue 23, 2007, p. 86-92.
-
Okatan A., Hajiyev C., Hajiyeva U. Fault detection in sensor information fusion Kalman filter. AEU – International Journal of Electronics and Communications, Vol. 63, Issue 9, 2009, p. 762-768.
-
Li D., Liu J. Y., Qiao L., Xion Z. Fault tolerant navigation method for satellite based on information fusion and unscented Kalman filter. Journal of Systems Engineering and Electronics, Vol. 21, Issue 4, 2010, p. 682-687.
-
Xu X. B., Feng H. S., Wang Z., Wen C. L. An information fusion method of fault diagnosis based on interval basic probability assignment. Chinese Journal of Electronics, Vol. 20, Issue 2, 2011, p. 255-260.
-
Moosavian A., Ahmadi H., Tabatabaeefar A. Fault diagnosis of main engine journal bearing based on vibration analysis using Fisher linear discriminant, K-nearest neighbor and support vector machine. Journal of Vibroengineering, Vol. 14, Issue 2, 2012, p. 894-906.
-
Li Z. X., Yin X. G., Zhang Z., He Z. Q. Wide-area protection fault identification algorithm based on multi-information fusion. IEEE Transactions on Power Delivery, Vol. 28, Issue 3, 2013, p. 1348-1355.
-
Dong Z. S., Zhang X. J., Zeng J. C. Fault diagnosis for hydraulic system on a modified multi-sensor information fusion method. International Journal of Modelling, Identification and Control, Vol. 18, Issue 1, 2013, p. 34-40.
-
Sarkar S., Sarkar S., Mukherjee K., Ray A., Srivastav A. Multi-sensor information fusion for fault detection in aircraft gas turbine engines. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, Vol. 227, Issue 2, 2013, p. 1988-2001.
-
Hang J., Zhang J. H., Cheng M. Fault diagnosis of wind turbine based on multisensors information fusion technology. IET Renewable Power Generation, Vol. 8, Issue 3, 2014, p. 289-298.
-
Xu L., Xu J. P. Sensory information fusion-based fault diagnostics for complex electronic systems. Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability, Vol. 230, Issue 1, 2016, p. 109-119.
-
Cheng G., Chen X. H., Shan X. L., Liu H. G., Zhou C. F. A new method of gear fault diagnosis in strong noise based on multi-sensor information fusion. JVC/Journal of Vibration and Control, Vol. 22, Issue 6, 2016, p. 1504-1515.
-
Xiong J. B., Zhang Q. H., Sun G. X., Zhu X. T., Liu M., Li Z. L. An information fusion fault diagnosis method based on dimensionless indicators with static discounting factor and KNN. IEEE Sensors Journal, Vol. 16, Issue 7, 2016, p. 2060-2069.
-
Sun J., Feng B., Xu W. B. Particle swarm optimization with particles having quantum behavior. Proceedings of Congress on Evolution Computation, 2004, p. 325-331.
-
Jin C., Jin S. W. Parameter optimization of software reliability growth model with S-shaped testing-effort function using improved swarm intelligent optimization. Applied Soft Computing, Vol. 40, 2016, p. 283-291.
-
Blasone M., Jizba P., Kleinert H. Quantum behaviour of deterministic systems with information loss: path integral approach. Annals of Physics, Vol. 320, 2005, p. 468-486.
-
Pan Z. Q., Zhang Y., Kwong S. Efficient motion and disparity estimation optimization for low complexity multiview video coding. IEEE Transactions on Broadcasting, Vol. 61, Issue 2, 2015, p. 166-176.
-
Gu B., Sheng V. S., Tay K. Y., Romano W., Li S. Incremental support vector learning for ordinal regression. IEEE Transactions on Neural Networks and Learning Systems, Vol. 26, Issue 7, 2015, p. 1403-1416.
-
Gu B., Sheng V. S., Wang Z. J., Ho D., Osman S., Li S. Incremental learning for ν-support vector regression. Neural Networks, Vol. 67, 2015, p. 140-150.
About this article
The authors would like to thank all the reviewers for their constructive comments. This research was supported by the National Natural Science Foundation of China (51605068, 51475065, U1433124), Open Project Program of State Key Laboratory of Mechanical Transmissions (Chongqing University) (SKLMT-KFKT-201513, SKLMT-KFKT-201416), Science and technology project of Liaoning Provincial Department of Education (JDL2016030, L2014191), the Natural Science Foundation of Liaoning Province (2015020013), Doctoral Scientific Research Foundation of Liaoning Province (201601264), Open Project Program of the Traction Power State Key Laboratory of Southwest Jiaotong University (TPL1403), PAPD and CICAEET. The program for the initialization, study, training, and simulation of the proposed algorithm in this article was written with the tool-box of MATLAB 2010b produced by the Math-Works, Inc.
Huimin Zhao conceived the research subject and contributed to feature extraction, Wu Deng contributed to information fusion method, Xinhua Yang contributed to fault diagnosis method, Xiumei Li contributed to carried out the experiments and Zhengguang Li contributed to improved PSO algorithm. All authors have read and approved the final manuscript.
