Abstract
The term ‘vibroacoustics’ is nowadays a commonly used notion of interdisciplinary scientific domain which links the elements of the vibration theory and theoretical acoustics with practical (engineering) methods of solving problems in the field of vibrations and noise minimization using increasingly developing measurement methods (observations). Unanswered remains the question whether the discipline defined in such a way constitutes a separate study and therefore needs implementation of its own axiomatics which orders the domain and facilitates teaching. This paper shows that the lack of uniform fundamental assumptions might easily lead to serious mistakes.
1. Introduction
The concept of vibroacoustics was developed nearly half a century ago. It immediately aroused a great controversy, both to the justification of the used term and the areas of knowledge that are hidden under that term.
Fig. 1Basic vibroacoustic tasks according to [1]
![Basic vibroacoustic tasks according to [1]](https://static-01.extrica.com/articles/16693/16693-img1.jpg)
These controversies did not come from nothing. There had to be the reason, other than the usual “inertia” reluctance, to a new approach to the problem.
In order to answer the question if the vibroacoustics constitutes a separate scientific domain, it is important to quote the definition of this term given by the undisputed creator of this discipline professor Zbigniew Engel. He stated, inter alia, in [1, 2]: “Vibroacoustics is the branch of science which deals with every vibration and acoustic problems which are present in the nature, techniques, machines, devices, means of transport and communication, therefore in the environment”. What is more, “The utilitarian aim of vibroacoustics is decreasing vibroacoustic noises of the machines, devices, installations and the surroundings to the minimum, possible at this stage of knowledge and technology, and using the information contained in the vibroacoustic signal to assess the quality of machines, devices, constructions, etc. and implemented technological processes”. The aim defined in such a way implies basic tasks of vibroacoustics, e.g. according to the scheme presented in Fig. 1.
2. The need for axiomatization of the subject
Each separate scientific discipline has to fulfill a few basic conditions in order to be worthy of the name. These conditions are:
1. A well-defined research area.
2. Axiomatics (preliminary assumptions, basic quantities of empirical knowledge).
3. A deductive system allowing for reasoning a’priori and a’posteriori.
Vibroacoustics was created in order to realize the postulate that the noise and mechanical vibrations can be considered together as similar forms of energy propagation, predominantly parasitic [3-5] (however, it happens often that this energy is used in vibrating machines), which constitute the source of information about the object condition.
Fig. 2Area of vibroacoustics application
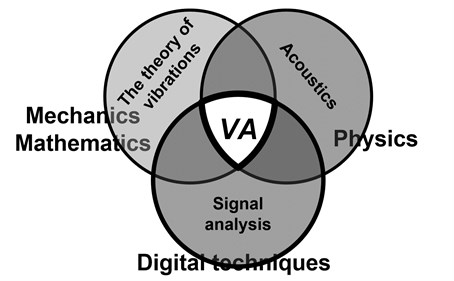
Thus, in natural way, since the beginning of its existence it constituted the combination of vibration and acoustic theory – two well-defined disciplines. However, it is still not enough to talk about the new study. The vibration theory and theoretical acoustics are separate fields of physics (mechanics) where the reasoning is based on the language of differential equations (ordinary and partial). Thus, attempts of “connecting” them do not bring any new values, except to say that the researcher willing to deal with the effect of vibrations and noises of machines on the environment should be the expert in both theories. Thus, the subject separateness of vibroacoustics demanded at least a different view on the research results (sometimes used deliberately) of both disciplines. It is worth mentioning at this point that vibroacoustics shaped its present form at a time when engineering calculations were performed on the slide rule. The vibration theory waded into a blind alley of approximate theoretical solutions of nonlinear differential equations considering issues practical realization of which was becoming increasingly difficult. The engineers were not interested in calculating “discoveries” of researchers. They expected algorithms, recipes which could answer the question what to do to minimize vibrations and machine noises or what to do in order to extract the expected diagnostic information from the observed process [11-13]. Not so long ago, the only reliable vibroacoustic diagnostic analyzer was the ear of an experienced practitioner. The gap between the science and practice opened up quite strongly, which made designers and manufacturers of technical devices performing experimental research.
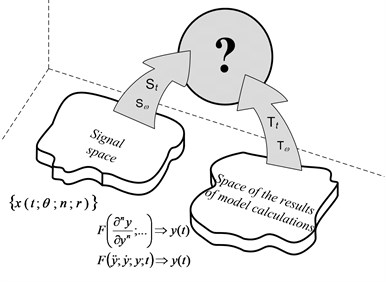
Fig. 3Schematic illustration of the common space of observation and model solutions
A good reflection of the state of the theory ↔ practice relation (from the mid 60s of the last century) is an excellent book written by Chihiro Hayashi “Nonlinear Oscillations in Physical Systems” [6]. These days, it only gives rise to reflection how much is needed in order to learn how to find a few examples illustrating the theory. The developing vibroacoustics somehow broke the deadlock in the development of both theoretical sciences (acoustics and vibration theory). Since the very beginning of vibroacoustics the experimental research accompanied their theoretical achievements. Such combination brought a different (new) point of view on the examined phenomena, and filtered out from theoretical sciences only results and methods physically realizable. It can be stated that at this point the authors of the discipline “struck home” because the information revolution provided an excellent tool which is the developed analysis of signals. Ipso facto, vibroacoustics might be classified as an interdisciplinary science which works in a common area of the vibration theory, acoustics, and measurements of dynamic values according to the scheme presented in Fig. 2 [2, 7].
However, is defining this common area the same as possessing “own axiomatics and language”? Let us look at the following problem: the vibration theory and acoustics provided (and is still providing) vibroacoustics with mathematical models. The signal analysis brought interpretation of observations into practice. Vibroacoustics must combine it somehow. It must have the language which allows for a common interpretation of model calculation results and measurement results. Thus, it is possible to define the fundamentals of the subject based on the observed signal ↔ mathematical model relationship.
However, how to write down such a relation? The results of observations are a kind of a random process which possesses inevitable errors. These errors result from an imperfection of measuring methods and – in many cases – from a lack of the possibility to realize a direct observation of the phenomenon which is interesting for us. The effect of model calculations is usually the set (space) of determined solutions of a differential equation system, often “invisible” for a researcher who uses modern simulation techniques. The main problem, thus, is to define a mapping that allows to bring the results of observations and calculations to a common space (best metric). This task is presented schematically in Fig. 3.
Assuming that this is possible, let us try to write the general relation signal ↔ model in the form:
where the left hand side is a selected part of the observed signal which, in general, is the random process dependent on time , the recording device location , device specimen , and evolutionary life time , whereas the right hand side provides the results of model calculations with the admission of the error structure of model and measurement noise . Variable denotes here the excitation, and means the impulse response function (the fact that the linear model was used here is not significant since signal ↔ model relationship for the nonlinear model look similar, which was discussed in literature [8]). This relationship can be explained schematically by a certain philosophy of vibroacoustics operations: we expect consistency of results of the selected (interesting for us) part of observations with the mathematical model with the accuracy of imperfection of our description and measurement errors . On both sides of Eq. (1), two operators have been introduced. is the selection and averaging operator in the time-domain. This operator transforms a random process into a certain determined characteristics. The second introduced operator is operator of transformation of modeling results which is necessary in the case of indirect measurements and sometimes purposeful in order to obtain an equivalent of characteristics defined with operator . on the basis of solutions. If we define the common space of observation and results of modeling research in this way, we will introduce an appropriate metrics:
so that the relation Eq. (1) will have the features of the equation which allows for transformations, and in effect leads to the solution of e.g. the diagnostic task:
where is the damage parameter, and and are the life time parameters of different states or in a similar way the task of minimization of vibrations and noise influences on the environment, etc.
Such notation allows to bring the problem to the frequency domain according to the formula:
where means the Fourier transform (or other defined transform, e.g. a wavelet transform), is the filtering operator (selection in a frequency domain) and is an equivalent operator as in frequency domain.
Denoting left hand side of the Eq. (3) by and the right hand side by we can define the basic tasks of vibroacoustics as follows:
1. Identification of the mathematical model:
where – maximal identification errors.
2. Diagnostic task:
3. Vibration and noise minimization:
4. Synthesis of vibrating system:
The properly written signal ↔ model relationship can act as the fundamental assumptions (axioms) of vibroacoustics. However, is such procedure practical? Let us analyze a simple example of the diagnostic task.
3. Example
Axiomatic systematization of vibroacoustics is useful in didactics, however, defining the problem precisely may have significant meaning and it may allow for eliminating serious mistakes. Let’s analyze a diagnostic problem as an example which is connected with searching for vibration symptom of damage (wear) of the gear of the fifth transmission gear of a car. The experiment was carried out in order to solve the problem. Fiat Punto was the object which was tested. There were registered the vibrations of gear housing at steady motion with rotational speed of engine 3000 RPM. The spectral structure was analyzed in the neighborhood of harmonic I and II of the meshing frequency. It was expected that there will appear nonlinear effects in these bands [3]. In particular, there may appear modulation with meshing frequency whose changes are known diagnostic symptom [9, 10].
The problem can be theoretically defined in the following way:
where and mean the change of state, is a model (theoretical) sequence of Fourier discreet components, and and are the variables of the state.
After appropriate defining the metric and subtracting sides of the equations, it is possible to find the difference of variables and i.e. finding the evolution of diagnostic symptom. Although the problem is apparently complicated, it seems to be relatively simple and it comes to comparing selected components of Fourier spectrum:
where is the frequency of meshing, is the rotational frequency (modulating).
The operator of selection was taken as:
where is Hanning window, is the operator of discretization.
The research, however, showed the impossibility of a simple solution of the problem because the spectrum obtained from the analysis carried out with the given parameters looks like in Fig. 4 and it is far from the model spectrum (it is difficult to extract the components we are interested in).
Using additional filtering around the anticipated theoretical frequencies is also insufficient because total level of several spectral harmonics which are close to each other is rather unrepeatable.
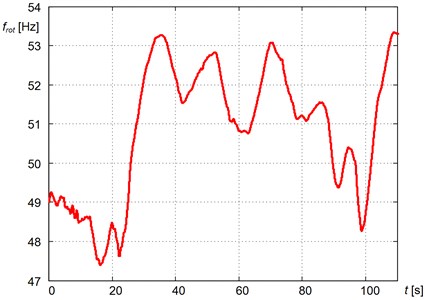
As the research showed, the reason for this are small changes of rotational speed of engine around “constant” speed (Fig. 5).
Thus, the axiom of common space of signals and model values is not fulfilled! In this case it is important to redefine the operator of selection in time domain. The signal should be sampled with a variable step in such a way so that the sampling would be for the same angle increments of crankshaft rotation . That is why, the operator of selection is used according to the following formula:
where is Dirac delta function, is a constant step of sampling the angle of rotation of crankshaft, – selected points of time corresponding to constant increment of the angle, is the frequency of sampling.
Fig. 4Spectrum of vibrations of gear housing in selected interval for a simple operator of selection
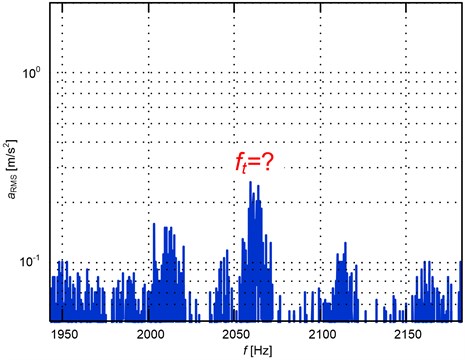
Fig. 5The change of rotational frequency of the engine during the vehicle motion with a “constant” speed
The signal obtained in this way corresponds to “ideally” steady movement. Discreet components of Fourier spectrum are the elements for the same space as the model components. The principle of operation of the operator including the variable step of sampling is presented in Fig. 6.
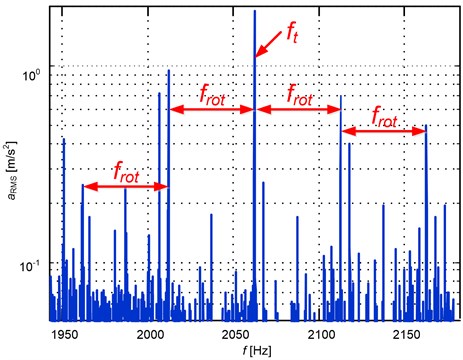
As a result of the use of such an operator there was obtained the observed spectrum of signal presented in Fig. 7 with clearly separated components corresponding to theoretical model.
Such an observation can be the basis for diagnostic concluding with the use of differently defined metrics which include the differences of amplitudes with the same meshing frequency and side modulation bands:
Since the results and the model belong to the same space, it is also possible to find relationship state ↔ symptom:
Fig. 6The principle of operation of redefined operator of selection in time domain: a) the choice of step for Δφ=const, b) signal resampling
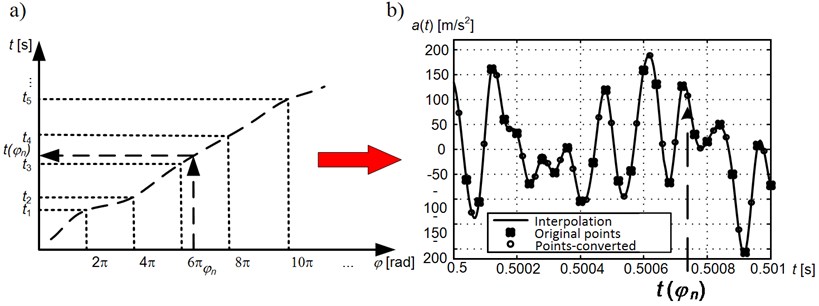
Fig. 7Spectrum of signal after resampling
4. Conclusions
The adequate definition of the selection operator St allowed to obtain the spectral characteristics useful for the diagnostics aims. Thus, this example confirms the necessity of the precise defining the initial relationship: signal ↔ model. Thereby, it should be expected that the formal putting in order the vibroacoustic axiomatics is appropriate also from purely practical reasons, not to mention the facilitation of this subject lecturing. In the authors opinion, the proposal to consider the relationship of signal ↔ model together with defining Eqs. (4)-(7), as the bases for considerations, should help in the final, comprehensive, arrangement of vibroacoustics as a separate, ‘full-fledged’ scientific discipline.
References
-
Engel Z., Piechowicz J., Stryczniewicz L. Fundamentals of Industrial Vibroacoustics. AGH, Kraków, 2003, (in Polish).
-
Crocker M. J. Handbook of Noise and Vibration Control. John Wiley and Sons, 2007.
-
Batko W., Dąbrowski Z., Kiciński J. Nonlinear Effects in Technical Diagnostics. Publishing and Printing House of the Institute for Sustainable Technologies – NRI, Warsaw, 2008.
-
Batko W., Dąbrowski Z., Engel Z., Kiciński J., Weyna S. Modern Methods for Noise and Vibration Testing Processes. Publishing and Printing House of the Institute for Sustainable Technologies – NRI, Warsaw, 2008, (in Polish).
-
Bendat J. S. Nonlinear Systems Techniques and Applications. John Wiley and Sons Inc., New York, 1998.
-
Hayashi Ch. Nonlinear Oscillations in Physical Systems, Princeton University Press 1986.
-
Bendat J. S., Piersol A. G. Random Data: Analysis and Measurement Procedures. 4th Ed., John Wiley, New York, 2010.
-
Dąbrowski Z. Diagnostic inferring on the bases of nonlinear models. Acta Physica Polonica A, Vol. 118, Issue 1, 2010, p. 45-48.
-
Klekot G. Simplified kinematic model of a spur gear with involute teeth elaborated for analysis of gear vibroactivity. Machine Vibration, Vol. 1, Issue 4, 1992, p. 261-267.
-
Dziurdź J. Modelling of the toothed gear operations with the application of the analysis of the gear sliding mesh velocity changes. Solid State Phenomena, Vol. 180, 2012, p. 200-206.
-
Folęga P., Siwiec G. Numerical analysis of selected materials for flexsplines. Archives of Metallurgy and Materials, Vol. 57, Issue 1, 2012, p. 185-191.
-
Burdzik R., Folęga P., Łazarz B., Stanik Z., Warczek J. Analysis of the impact of surface layer parameters on wear intensity of friction pairs. Archives of Metallurgy and Materials, Vol. 57, Issue 4, 2012, p. 987-993.
-
Konieczny Ł., Burdzik R., Figlus T. Possibility to Control and Adjust the Suspensions of Vehicles. Activities of Transport Telematics, The Series Communications in Computer and Information Science, Springer, Heidelberg, Vol. 395, 2013, p. 378-383.
