Abstract
Nonlinear interaction of quasiharmonic longitudinal waves, which propagate in solid porous material, was investigated theoretically. It was shown that as a result of such interaction between low-frequency waves (vibration field) and high-frequency waves (ultrasound) an ultrasound wave of summarized frequency would be generated. This newly generated wave can be in a phase-group synchronism with the vibration field. Analytical analysis qualitatively agrees with experimental data of ultrasound generation through seismic load.
1. Introduction
Nonlinear wave dynamics of solids has been studied widely in the near past [1-5]. It was shown before that nonlinear wave effects are more vivid in structurally-imperfect materials and can be described using continuum equations with microstructure. The influence of material structure on the deformation processes can be estimated through taking into account the inner degrees of freedom (rotational, oscillatory) of structure elements in unit volume.
Typical example of such a medium with oscillatory degrees of freedom is porous material. To describe dynamics of porous materials mathematical models are being used that are built on concepts close to the ones in mechanics of fluids with gas bubbles [6].
Three-dimensional model of porous material was proposed in [7].
From wave theory, it is well known that in case of quadratic nonlinearity an effective exchange of energy is possible between a set of three waves. One wave can break into two or two waves can join into one. Frequencies and wave numbers of such waves are connected of phase-group synchronism condition and comply with dispersive relations.
Quite interesting is the situation, where interacting waves have frequencies which differ greatly from each other, but phase velocity of low-frequency wave is equal to group velocity of high-frequency wave.
This situation is common for various physical problems [8-11]. In these problems high-frequency wave generates a low-frequency wave.
In seismicity, a different situation has been observed experimentally, described in [12]. Low-frequency vibration excitation on the earth beds generates ultrasound. And ultrasound generation was most effective if phase-group synchronism held true.
In this paper it is shown that the studied model of porous material allows description of generation of ultrasound as a result of low-frequency field with another ultrasonic wave.
2. Mathematical model
Preliminary assumptions are the following: the main medium is isotropic; distance between the cavities is a lot larger than radius of a cavity and at the same time is a lot smaller than the length of the wave that propagates in the material .
Suppose the propagating wave is longitudinal, i.e. pressure on the cavity is determined by longitudinal stress , where , – number of cavities in the unit volume, – volume of a cavity (), – initial volume of a cavity, а – volume of a cavity indignant by a wave.
Propagation of a plane wave in porous material can be described by the following system of two nonlinear equations:
In equations – initial density of the material, – square of the resonant frequency of a cavity volume oscillation, – square of the longitudinal wave velocity, – coefficient, caused by geometrical and physical nonlinearities, , , – Landau constants of the third order.
The first equation of Eq. (1) describes deformation wave in material with cavities that takes into account the oscillation of the cavity volume. Second equation describes the process of cavity volume oscillation under the influence of wave propagation in the main matrix.
In linear approximation of Eq. (1) dispersive properties can be studied. They are described by the following equation:
where – is angular frequency, – wave number, – wavelength (spatial analogue of a period).
Longitudinal wave that propagates in the material has dispersion, i.e. its phase velocity . In a frequency range from to:
where ; there is one dispersive branch and at dispersive branch appears.
We define as porosity and study porosity influence on wave dispersion. Expression for porosity can be obtained from the ratio of total volume of material to the volume of spherical cavities that exist in it taking condition into account. This will lead to the following expression for porosity:
where is a number of wavelengths, which defines the volume of the sample in cubic meters as .
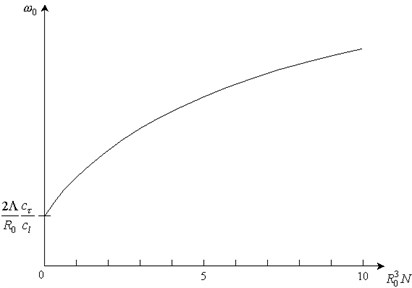
Dependence of dispersive properties on the porosity is shown characteristically in Fig. 1 and of value in Fig. 2.
3. Evolutionary equations
It is a rather complex task to investigate propagation of waves of finite amplitude in porous materials even if it is a one-dimensional process as considered in Eq. (1). It is significantly easier to deal with evolutionary equations, which are being an approximation contain the basic factors that influence wave processes. There are several physically and mathematically correct methods of transformation of original equations to evolutionary ones [14]. We use the method of coupled normal waves for which we rewrite Eq. (1) in the form:
where is a four dimensional vector of physical variables:
is linear operator matrix, – differentiation operator; – vector of nonlinear values.
Fig. 1Dependence of frequency of propagating elastic wave on wave number and porosity
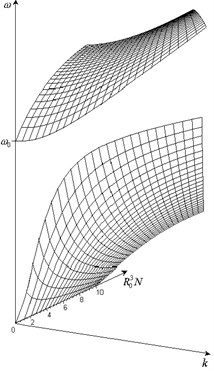
Fig. 2Dependence of ω0 on porosity
Transfer from Eq. (3) to equations of coupled normal waves is done through diagonalization of operator matrix by transforming it into proper basis using the following change of variables:
where are new variables, – right eigenvectors of the matrix ; – eigenvalues of the matrix .
Substitute Eq. (4) into Eq. (3). Multiply them by the left eigenvectors and using orthogonality condition at we arrive to the equations of coupled normal waves where defines different branches of dispersive equation of the linearized system. Freedom in choosing eigenvectors can be used to bring the right hand side to the simplest form. Using this freedom and expanding eigenvalues into Taylors series by taking into account first two components we arrive to the following evolutionary equations:
where is a complex conjugate of :
Connection between new variables with original ones is defined by:
For and system Eq. (5) is complex conjugated Schrödinger equations, and for and – KdV equations. Nonlinearity causes these four equations to be connected.
Fig. 3Dependence of frequency of the propagating elastic wave on wave number with porosity being constant
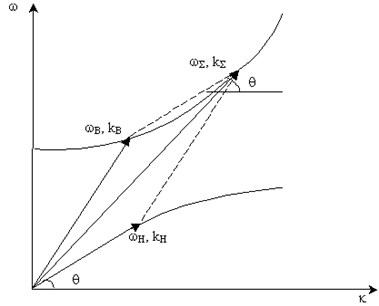
Analysis of Eq. (5) shows that in a large frequency range evolutionary equations approximate dispersive dependences of the original equations very well. Dispersive dependences for original and evolutionary equations are shown in Fig. 3. The comparison was carried out using physical parameters of two-layered boron-carbonaceous-phenol composite as an example of solid mixture and physical parameters of highly porous sandstone as an example of porous media.
Eq. (5) allows estimation of “porous” nonlinearity contribution into total nonlinearity. This can be done through analyzing dependence of nonlinearity coefficient on porosity.
With the increase of porosity and under condition of nonlinearity coefficient is defined by , i.e. linearly grows with an increase of porosity and can be in of a value of order two or three, which agrees well with experimental data [15].
4. Interaction of quasiharmonic waves analysis
Consider that in a positive direction of axis a wave propagates with a frequency and wave number and a wave propagates with a frequency and wave number . Suppose , i.e. identifies vibration field and identifies ultrasound.
As a result of their interaction on a quadratic nonlinearity of system Eq. (5) there will be generated a wave of summarized frequency, which comply with conditions of three waves resonant interaction:
Frequency and wave number of vibration field must comply with the law of dispersion for KdV equation:
and frequencies and wave numbers of the ultrasound must comply with the law of dispersion of Schrödinger equation, i.e. the following:
Ultrasound wave of summarized frequency must, according to the problem statement, comply with conditions of phase-group synchronism, i.e.:
where is group velocity of ultrasound and is phase velocity of vibration field.
To determine frequencies and wave numbers at which these processes are possible, a system of algebraic equations Eqs. (8)-(13) should be solved. This system can be solved analytically under a consideration that condition Eq. (13) will be reduced to:
since contribution of value into phase velocity of vibration field is negligibly small.
From the solution of Eqs. (8)-(12), and (14) values for wave frequencies that are in a phase-group synchronism can be found:
Solution of Eqs. (8)-(13) is shown graphically in Fig. 3. At that .
From analysis of ratio parameters of the model of porous material at which the process of phase-group synchronism is possible, can be found. At ~ 102 number of cavities in the unit volume will be of a value ~ 105 with radiuses ~ 10-2 m., and from Eq. (2) volume of the porous material for given wavelengths can be found.
5. Modulation instability
Let the ratio of characteristic wave number of vibration field over wave number of ultrasound field be rather small. We use the traditional transition into a moving coordinates system with a different time and spatial scale:
Due to the introduction of new independent variables , the derivatives and will be transformed according to the following law:
Transforming in Eq. (5) (at ) to the new variables we arrive to:
Here in addition to the new variables and time Eq. (16), functions and :
where – identifies a complex conjugate value.
In case of no resonance () the second component in the first equation of Eq. (17) becomes a lot smaller than the first component, which results in and allows bringing Eq. (17) to one nonlinear Schrödinger equation for the complex amplitude of the ultrasonic wave:
In the resonant case there is such , at which , i.e. group velocity of short ultrasound waves coincides with phase velocity of long vibration signals.
From resonant condition wavelength of the newly generated ultrasound can be obtained:
The stricter the condition is executed the more precise the approximation of long-short wave resonance is obtained. Here is wavelength of a low-frequency wave and . The last inequality follows from the dispersive equation Eq. (10) and means that the most effective resonance can be reached in the linear part of dispersive branch of KdV equation.
It is known that in a cubic-nonlinear medium a quasiharmonic wave can become instable to its fragmentation into wave packets. This phenomenon is called modulation instability or self-modulation [13].
Presence of modulation instability can be defined from Eq. (17) with a help of Lighthill criterion and occurs in the studied system, if:
Since from Eq. (6) it follows that , , , then Eq. (21) is equivalent to inequality:
Hence, spatial localization of the ultrasound wave will be observed until appearance of phase-group synchronism.
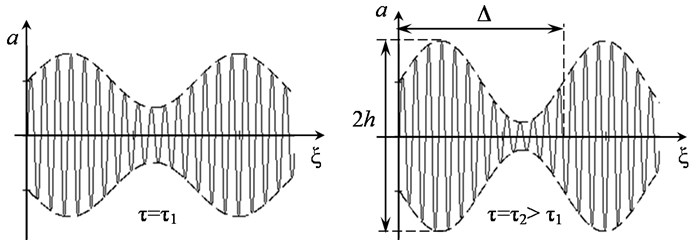
A self-modulation effect in spectral terms is characterized by increase in sideband components in modulated wave spectrum. These components will be pumped by energy from central part of spectrum of the disturbance. The self-modulation process is schematically shown in Fig. 4(a), and Fig. 4(b) illustrates evolution of its spectrum.
Fig. 4a) Self-modulation process of wave and b) evolution of its spectrum (ω* – center frequency)
a)
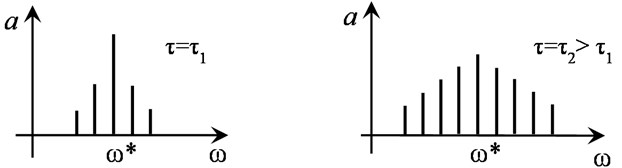
b)
We introduce real amplitude and real phase instead of a complex amplitude : . Then Schrödinger equation Eq. (19) can be rewritten as a system of equations:
Next, we should define the form of wave packets into which quasiharmonic wave is breaking as a result of modulation instability. System of equations Eq. (23) can be used to analyze stationary envelope waves.
Look for a solution of Eq. (23) that depends on one variable where is a velocity of stationary wave: , .
Then system of equations in partial derivatives Eq. (23) will transform into a system of two ordinary differential equations. After integration of the first one we arrive to the connection between phase of the wave and its amplitude:
where is an integration constant.
If we bound ourselves to considering waves with amplitude modulation only and without phase modulation then 0, and change of amplitude will be described by Duffing equation:
here ; .
In the area of modulation instability Eq. (22) this equation has periodical solution, defined by Jacobis elliptic cosine:
Here is a module of elliptic function (); is an amplitude of envelope wave; is a nonlinear analogue of wave number, connected with wavelength of envelope wave () and full elliptic integral of the first type () by the expression .
Form of the envelope wave is defined by the module of elliptic function (), which in turn depends on the value and therefore characterizes degree of nonlinear distortion of a wave packet. For small amplitudes and form of envelope wave is close to sinusoid. For large amplitudes and form of the envelope wave becomes saw-toothed.
Next we determine the connection between the height () and width () of wave packet, which forms as a result of self-modulation of quasiharmonic wave, with the basic characteristics of the medium and with correlation between phase velocity of vibration field and group velocity of ultrasound.
We identify the height of wave packet with doubled amplitude and its width with a half of wavelength of envelope wave and arrive to:
Analysis of these expressions shows that height of wave packet increases and its width decreases with an increase of velocity of envelope wave (; ) and with an increase of porosity (; ).
Thus, based on nonlinear mathematical model of solid porous material, a theoretical investigation of phase-group synchronism during elastic longitudinal wave propagation was carried out. In [1, 12] it was noted that particularly in this regime generation of ultrasound in the earth beds by low-frequency seismic excitations becomes possible.
6. Conclusions
The model of porous material considered in the paper allows description of generation ultrasound as a result of low-frequency field with another ultrasonic wave. From condition of phase-group synchronism possibility the relations to determine parameters of the model of porous material, such as number of cavities in the unit volume, cavities radiuses and volume of the porous material for given wavelengths, are obtained. Modulation instability results in quasiharmonic wave breaking into wave packets. Form of the envelope wave is defined by the module of elliptic function which characterizes degree of nonlinear distortion of a wave packet. For small amplitudes 0 and form of envelope wave is close to sinusoid, while for large amplitudes 0,5 and form of the envelope wave becomes saw-toothed. Height of wave packet increases and its width decreases with an increase of velocity of envelope wave and with an increase of porosity.
The results of the research allow developing a control method of oil production in exploited for a long time high-water-cut deposits, and is based on the vibration and acoustic exposure on the oil-bearing strata.
References
-
Nikolaevskiy V. N. Geomechanics and Fluidodynamics. With Applications to Reservior Engineering. Kluwer Academic Publisher, The Netherlands, 1996.
-
Kulikovskii A. G., Sveshnikova E. I. Nonlinear Waves in Elastic Media. CRC Press, Boca Raton, London, 1998.
-
Samsonov A. M. Strain Solids in Soids and How to Construct Them. CRC Press, Boca Raton, London, 2000.
-
Erofeyev V. I. Wave Processes in Solids with Microstructure. World Scientific, New Jersey, London, Singapore, Hong Kong, 2003.
-
Porubov A. V. Amplification of Nonlinear Strain Waves in Solids. World Scientific, New Jersey, London, Singapore, Hong Kong, 2003.
-
Nakoryakov V. E., Pokusaev B. G., Shreiber I. R. Wave Propagation in Gas-Liquid Media. CRC Press, Boca Raton, Ann Arbon, London, Tokyo, 2003.
-
Bagdoev A. G., Shekoyan A. V. Nonlinear waves in solid viscous medium with cavities. Acoustical Physics, Vol. 45, Issue 2, 1999, p. 119-126.
-
Zakharov V. E. Collapse of Langmuir waves. Journal of Experimental and Theoretical Physics, Vol. 35, Issue 5, 1972, p. 908-914.
-
Benney D. J. Significant interactions between small and large scale surface waves. Studies in Applied Mathematics, Vol. 55, Issue 2, 1976, p. 93-106.
-
Benney D. J. General theory for interactions between short and long surface waves. Studies in Applied Mathematics, Vol. 56, Issue 1, 1977, p. 81-94.
-
Zozulya O. M., Rybak S. A. One-dimensional modulation instability of wave trains in media with resonance dispersion. Acoustical Physics, Vol. 44, Issue 2, 1998, p. 232-234.
-
Nikolaevski V. N., Stepanova G. S. Nonlinear seismics and the acoustic action on the oil recovery from an oil pool. Acoustical Physics, Vol. 51, Issue 1, 2005, p. 131-139.
-
Whitham G. B. Linear and Nonlinear Waves. John Wiley and Sons, New York, 1974.
-
Engelbrecht J. K., Fridman V. E., Pelinovsky E. N. Nonlinear Evolution Equations. Pitman, London, 1988.
-
Naugolnykh K. A., Ostrovsky L. A. Nonlinear Wave Processes in Acoustics. Cambridge University Press, Cambridge, 1998.
About this article
The research is carried out according to Ministry of Education and Science of the Russian Federation State Order No. 8.2668.2014/K, and Russian Foundation for Basic Research Project No. 15-08-01836.
