Abstract
This paper presents a fault diagnosis method for gearbox based on local mean decomposition (LMD), permutation entropy (PE) and extreme learning machine (ELM). LMD, a new self-adaptive time-frequency analysis method, is applied to decompose the vibration signal into a set of product functions (PFs). Then, PE values of the first five PFs (PF-PE) are calculated to characterize the complexity of the vibration signal. Finally, for the purpose of less time-consuming and higher accuracy, ELM is used to identify and classify of gearbox in different fault types. The experimental results demonstrate that the proposed method is effective in diagnosing and classifying different states of gearbox in short time.
1. Introduction
Rotating machinery has been widely used in the fields of aeronautics, astronautics, metallurgy and construction machinery [1]. Gearbox is an important and common transmission component in rotating machinery. Under the poor working environment, the gearbox is easy to break down. An unexpected failure of a gearbox may cause the sudden breakdown of rotating machinery, bringing about enormous financial losses or even personnel casualties [2-4]. Therefore, it is of great importance to conduct the research on the fault diagnosis of gearbox.
The key processes of gearbox fault diagnosis divide into two aspects: fault feature extraction and fault pattern identification [5]. Since the vibration signals of the gearbox are nonlinear and non-stationary, several time-frequency analysis methods have been proposed, such as wavelet transform (WT), empirical mode decomposition (EMD) and Hilbert Huang transform (HHT) [3]. WT has been widely used in fault diagnosis, but the wavelet basis function need be predefined or determined. Therefore, WT is not self-adaptive [6]. Contrarily, EMD, as a self-adaptive method, can decompose the signal into a series of intrinsic mode functions (IMFs), then combined with Hilbert transform (HT) to form HHT. However, some problems of EMD cannot be avoided, such as end effect, mode mixing phenomenon and meaningless negative frequencies.
LMD, another self-adaptive method, was proposed by Smith in 2005 [7]. LMD is used to decompose the vibration signals into a series of product functions (PFs). Every product function consists of an envelope signal and a frequency modulated signal. Compared with EMD, LMD has advantages in end effect and less mixing phenomenon, which can result in better decomposition results. Hence, LMD is applied to decompose the vibration signals in this paper. However, the PFs obtained from LMD are too large and complex to be taken as the fault feature vectors. Therefore, many methods such as approximate entropy (ApEn) [8] and sample entropy (SE) [9], have been investigated for fault feature extraction methods. These methods show a better performance in field of fault diagnosis of rotation machinery, however, each of them has its own shortcomings. ApEn depends on the data length, and the estimated value is lower than the expected value, especially for a short dataset. SE is insensitive to the data length and changes the standard deviation of time series [9, 10].
Permutation entropy (PE) was proposed by Bandt and Pompe for detecting the dynamic changes of time series [11, 12]. Compared with the above methods, the advantages of PE are simple, fast and immune to noise. PE has been widely used in numerous applications, such as electroencephalography (EEG) signals [13, 14], stock market analysis [15], and chatter detection in turning processes [16]. Due to the good performance of PE method, it is applied to calculate the PFs derived from LMD to obtain the multi-scale characteristics of the vibration signal. Meanwhile, the PE values of PFs (called PF-PE) are extracted as the feature vectors for fault type identification.
After the feature extraction, a classifier is required to identify the fault type accurately and automatically. Extreme learning machine (ELM), as an intelligent technology, has been proved to have better performance and less running time than the traditional algorithms, such as Back Propagation (BP) and supper vector machine (SVM) [17]. Moreover, ELM requires less human intervention, randomly choosing the parameters [18]. In this paper, ELM is applied to complete the state classification of gearbox.
The rest of the paper is organized as follows. Section 2 describes LMD method. PE is introduced in Section 3, while ELM is presented in Section 4. Section 5 offers the proposed diagnosis method and the experimental analysis. The conclusion is drawn in section 6.
2. LMD method
The essence of local mean decomposition (LMD) is to obtain a series of product functions (PFs) and a residual signal. Given the signal , it can be decomposed by LMD in the following steps:
(1) Find the total extreme (maximum and minimum) points of given signal, then calculate the mean value and the envelope estimate value using arbitrary successive extreme points and . So and are given by:
Connect all mean values by straight lines, then form the local mean function smoothed applying moving average. Get envelope estimate function in the same way.
(2) Separate the local mean decomposition from the original signal and obtain a new signal as:
Divide by to get as:
Obtain envelope estimate function corresponding to . If equals to one, is a pure frequency modulated signal. If not, repeat the above iterative procedures times until equals to one, now is a pure frequency modulated signal. So:
Among:
(3) Obtain the first envelope function through multiplying all envelope estimate functions produced in the iterative procedures:
(4) The first product function of original signal consists of the envelope signal and the pure frequency modulated given by:
(5) Subtract from the original signal , getting a new signal regarded as a new signal. Repeat the above procedure times until residue component is monotonic:
The original signal is decomposed into and a residue :
3. Permutation entropy method
3.1. Definition of permutation entropy
Permutation entropy was firstly introduced by Bandit to estimate the complexity of time series through comparing the neighboring values [19]. The algorithm of PE can be described as follows:
Given a time series , the dimensional vector at time can be defined as:
where represents the embedding vector and represents time delay.
has a permutation if it satisfies:
where and .
Aim at a -tuple vector, there are permutations. We define the relative frequency for each permutation as:
where is the number of satisfying the type .
PE with dimension can be determined by:
It is easy to find that the maximum value of is . So the normalized permutation entropy is:
It is obvious that satisfies . A larger value of means the time series is much more irregular. When the time series is white noise, obtains the maximum value (one). On the contrary, with the smaller value is more periodic and the minimum value is zero. Therefore, PE is used to estimate the complexity and dynamic change of a signal.
3.2. The parameter selection of permutation entropy
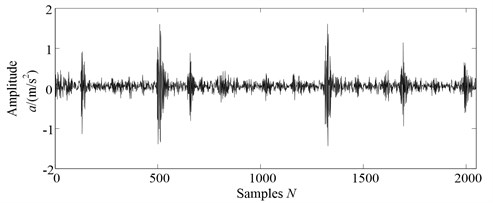
These parameters should be set before using PE, including embedding dimension , time delay and the length of the time series . In order to investigate the effect of each parameter in calculating PE value, an actual gearbox vibration signal is taken as the analyzed time series, which is shown in Fig. 1. Firstly, we conduct the research on the relationships between the PE values and length of the data . Fig. 2 illustrates the PE values calculated by using the different data length and embedding dimension , where the data lengths 128, 256, 512, 1024, 2048 are respectively computed under the embedding dimension 2-10. As can be seen from Fig. 2, when the data length is more than 512, the difference between the PE values with different data length is small. For example, when 6, the difference between PE value with 512 points and PE value with 2048 points is only 0.0420. Hence, when 6, the data length with more than 512 points is sufficient to obtain stable PE values.
Fig. 1The waveforms of vibration signal measured from gearbox experiment system
Secondly, the relationship between the PE values and time delay is investigated under the different dimension . Fig. 3 shows the PE values computed with different time delay and embedding dimension where 1-6 are selected to achieve the PE values under the dimension 2-10. The conclusion can be drawn from Fig. 3 that the time delay has little impact on the estimation of PE. For example, when 6, the difference of PE values between 1 and 6 is only 0.0085. Therefore, in this paper, we select time delay 1 in the following research.
Finally, the PE value highly depends on the selection of embedding dimension . Bandt and Pompe [19] proposed the permutation entropy method and indicated that the method works with the embedding dimension 37. In addition, Cao et al. [20] have discussed the validity of permutation entropy under different conditions of embedding dimension. Obviously, when embedding dimension is too small, the scheme will not work since there are too few distinct states. On the other hand, when embedding dimension is too large, it will lead to time consuming [21]. Embedding dimension is often selected by considering between information loss and computational complexity, is set to 6 in this paper.
Fig. 2The PE values of gearbox signals with different lengths
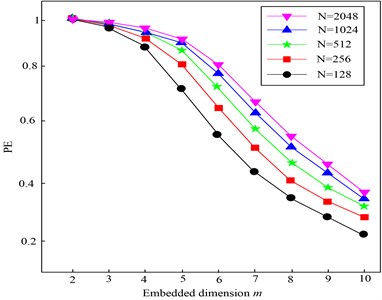
Fig. 3The PE values of gearbox signals with different time delays
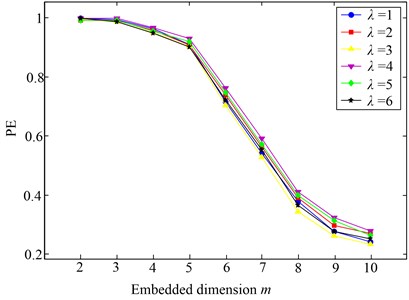
Fig. 4The MPE values of gearbox signals with different embedding dimensions
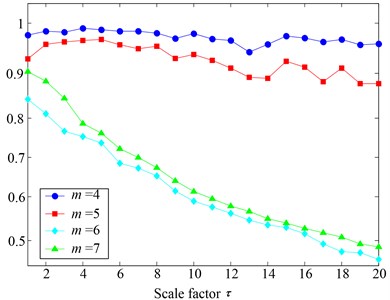
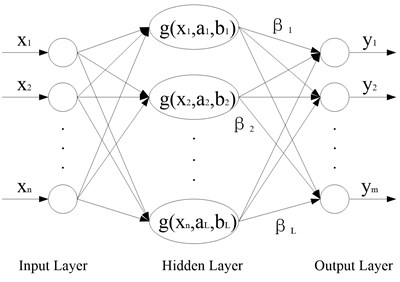
Fig. 5The structure of ELM
4. Extreme leaning machine algorithm
ELM as a new learning algorithm was proposed for single-hidden-layer feedforward neural networks (SLFNs), with good generalization and fast learning speed. The details of ELM algorithm can be seen in the literature [18, 22].
The structure of ELM is described in Fig. 5, where (1, 2,…, ) represents the input samples, represents the weights in the input layer, represents the offsets in the hidden layer, is the activation functions in the hidden layer, represents the weights in the output layer, represents the output matrix, is the number of nodes in the input layer, is the number of nodes in the hidden layer, is the number of nodes in the output layer, then the mathematical model of ELM is defined as:
It can be described as follows:
ELM tends to minimize not only the training error but also the norm of output weights. Thus, the output weights can be determined as follows:
where represents the Moore-Penrose generalized inverse of the hidden layer matrix. The details of Moore-Penrose generalized inverse matrix can be seen in the literature [23].
ELM is less sensitive selecting the activation function than SVM, so almost all nonlinear piecewise continuous functions can be regarded as activation [18].
1) Sigmoid function:
2) Hard-limit function:
3) Multiquadrics function:
4) Gaussian function:
Sigmoid function is selected as the major activation function in the feedforward neural networks and Gaussian function is applied in the radial basis function networks. Hard-limit function and multiquadrics function also show good performance in ELM algorithm. So sigmoid function is selected as the activation function in this paper and the procedure of ELM can be described as:
1) Determine the number of neurons in the hidden layer, then the activation function and arbitrarily assign , .
2) Calculate the output matrix of the hidden layer .
3) Calculate the output weight .
It should be noted that the MATLAB source code of ELM is available in the ELM portal, which can be obtained from http://www.ntu.edu.sg/home/egbhuang.
5. The proposed fault diagnosis method and experimental data analysis
5.1. The fault feature extraction based on LMD, PE and SVM
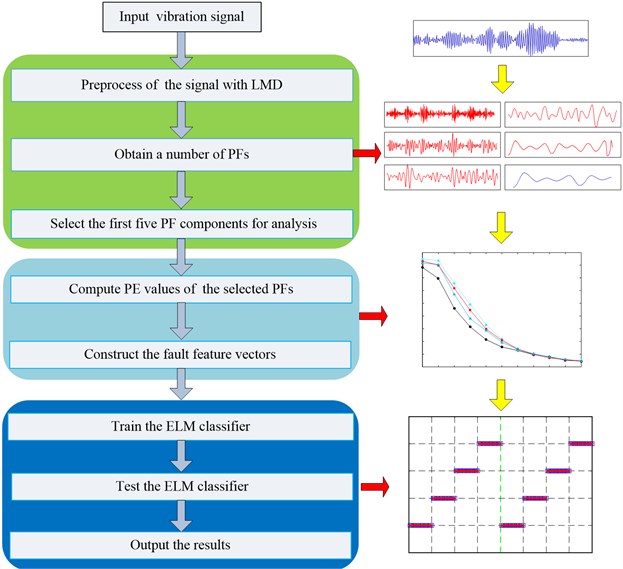
LMD has advantages in end effect and less mixing phenomenon compared with EMD, which can result in better decomposition results. The advantages of LMD has been verified by reference [26]. After a series of PFs are obtained using the LMD, the PE values of PFs (called PF-PE) are extracted as the feature vectors for fault type identification, compared with approximate entropy (ApEn) [8] and sample entropy (SE) [9], Permutation entropy (PE) are simple, fast and immune to noise. Lastly, ELM has been proved to require less human intervention and less running time than support vector machine (SVM) [18]. So in this paper, ELM is introduced for identification and classification of gear under different conditions. Based on the superiorities of LMD, PE and ELM, a novel gear fault diagnosis approach is proposed in this paper, the detailed steps can be summarized as follows:
1) When the gearbox under different working conditions, the vibration signals are acquired by acceleration sensors at a sampling frequency .
2) Partition the measured vibration signal into non-overlapping windows of suitable size .
3) Apply LMD method to analyze the measured vibration signal, and a number of PF components can be obtained. Then, the first five PF components that contain the most fault information are selected for further analysis.
4) Calculate PE values of the selected PF components using Eqs. (11)-(15) and generate the feature vector. Note that the obtained PE values of PF components are called PF-PE and the parameters of PE are set as follows: data length 2048, 6 and time delay 1.
5) The obtained fault features are fed into fault classifier ELM for training and testing to fulfill the fault diagnosis automatically. Note that the number of hidden neurons is assigned to 80 and sigmoid function is selected as the activation function in this paper.
A functional framework based on PF-PE and ELM algorithm is presented in Fig. 6.
Fig. 6Flowchart of the proposed algorithm
5.2. Experimental data analysis
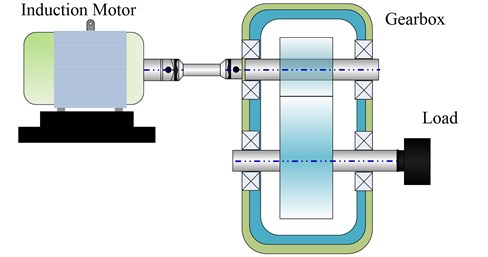
To illustrate the effectiveness of the proposed methodology in the real applications, experimental analysis on gear with slight wearing, severe wearing and missing tooth are conducted. The experiment is conducted on a test rig of the transmission gearbox, the layout and schematic sketch of the fault experiment platform are shown in Fig. 7(a) and (b), respectively. Two High Sensitivity Quartz ICP accelerometers were installed for data acquisition (one vertical, and one horizontal), the location of the accelerometer is on the base of floor stand. The speed of the motor is set to be 1500 rpm. Meanwhile, the sample frequency is 10000 Hz and the sampling time is 1 s. The fault gear is installed on the driven gear and the working parameter of the gearbox is listed in Table 1. Four working conditions are considered in this experiment: normal, slight wearing tooth, severe wearing tooth and the missing tooth. The wearing gear with different severities and gear with missing tooth are shown in Fig. 8, respectively.
Fig. 7The layout and schematic sketch of the fault experiment platform

a)
b)
Fig. 8The input fault position of gears

a) Slight wearing

b) Severe wearing

c) Missing tooth
Since the gear fault vibration is a multi-component, amplitude-modulated and frequency-modulated signal, the LMD method can decompose a complicated signal into a serial of PFs adaptively. So the LMD method is especially suitable for processing the gear fault signal. Firstly, the LMD method is applied to decompose the signal into a number of PFs, and then the PE values of the first five PFs are computed to construct the feature vectors. Finally, ELM is used to recognize the various fault types of gearbox [21].
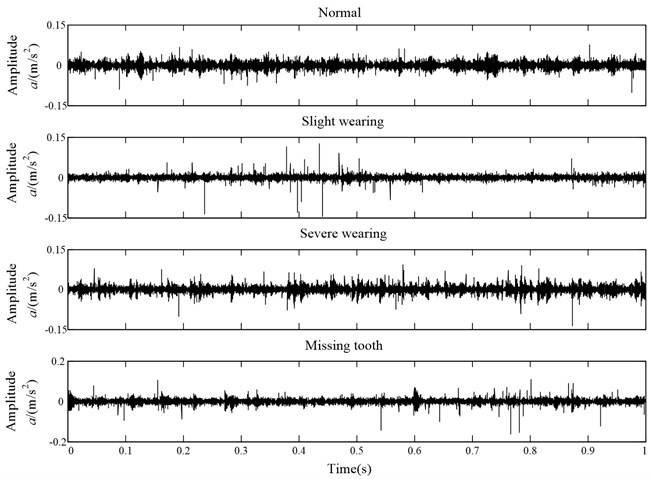
In this experiment, the collected vibration signals consist of four working conditions. Actually, the experimental analysis is a four-class recognition problem. The vibration signals are divided into several non-overlapping segments with the length 2048. Each condition has 40 samples, and there are total 160 samples, in which 80 samples will be randomly selected as the training data, while the remaining 80 samples are used to test the ELM classifier. The detailed numbers of samples description for each bearing condition are shown in Table 2. The time domain waveforms of vibration signals under four fault categories case are depicted in Fig. 9, respectively.
Table 1Working parameters of the gears
Gear | Number of teeth | Rotating frequency (Hz) | Meshing frequency (Hz) |
Driving gear | 55 | 25 | 1375 |
Driven gear | 75 | 18.33 | 1375 |
Table 2The detailed description of numbers of the experimental data sets
Fault class | Fault size (mm) | Class label | Number of training data | Number of testing data |
Normal | 0 | 1 | 20 | 20 |
Slight wearing | 0.1 | 2 | 20 | 20 |
Serve wearing | 0.5 | 3 | 20 | 20 |
Missing tooth | 0 | 4 | 20 | 20 |
Fig. 9The waveforms of gearbox vibration signal under four different conditions
Since the measured vibration signal has the characteristics of nonlinear and non-stationary, LMD is applied to decompose the vibration signal into a series of PFs. The decomposition results with four conditions (including: normal state, slight wearing fault, severe wearing fault and missing tooth fault) are illustrated in Figs. 10-13, respectively. Note that since the fault information contains mainly in the front PF components, only the first five PF components are plotted for saving space.
After completing the decomposition using LMD method, the PE method is utilized to extract the fault features according to the flowchart of the LMD and PE algorithm, which are described in Section 5. In this paper, the parameters of PE are set as follows: embedding dimension 6, time delay 1. To illustrate the advantage of the PF-PE for fault feature extraction, the PE values of the original vibration signals are also calculated for comparison. The PE values of different working conditions (including normal condition, slight wearing fault condition, severe wearing fault condition and missing tooth fault condition) are shown in Fig. 14. It should be noted that scale value 0 in the horizontal axis corresponds to the PE value of original signal and the scale values 1-10 in the horizontal axis correspond to the values of the first PF-PE value to the tenth PF-PE value [25].
Fig. 10LMD decomposition results of the vibration acceleration of gear with normal condition
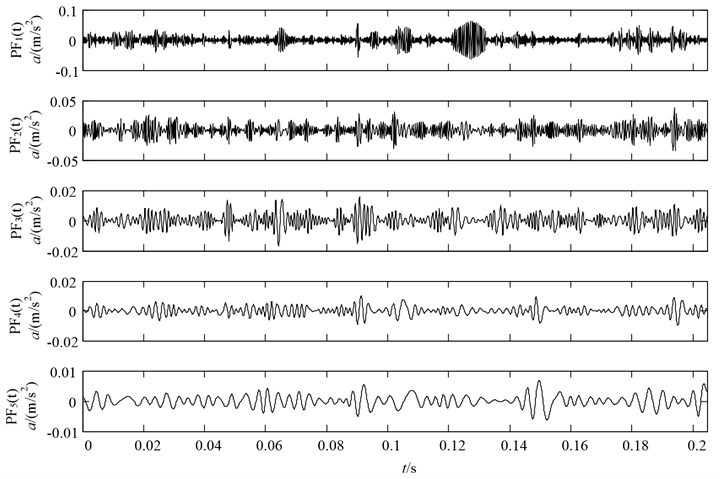
Fig. 11LMD decomposition results of the vibration acceleration of gear with slight wearing fault condition
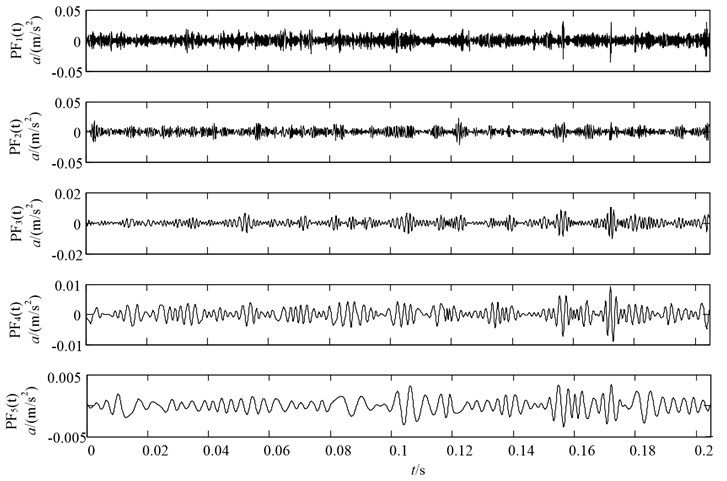
As seen from Fig. 14, the following conclusions can be got: Firstly, it can be observed from the PE of original signal (scale value 0) that PE can describe the gearbox under different working conditions. However, the PE values of fault conditions are too close to recognize them effectively.
Fig. 12LMD decomposition results of the vibration acceleration of gear with severe wearing condition
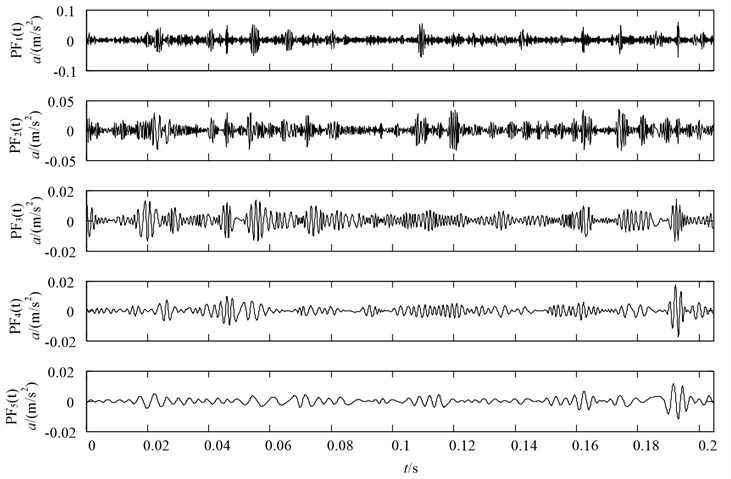
Fig. 13LMD decomposition results of the vibration acceleration of gear with missing tooth condition
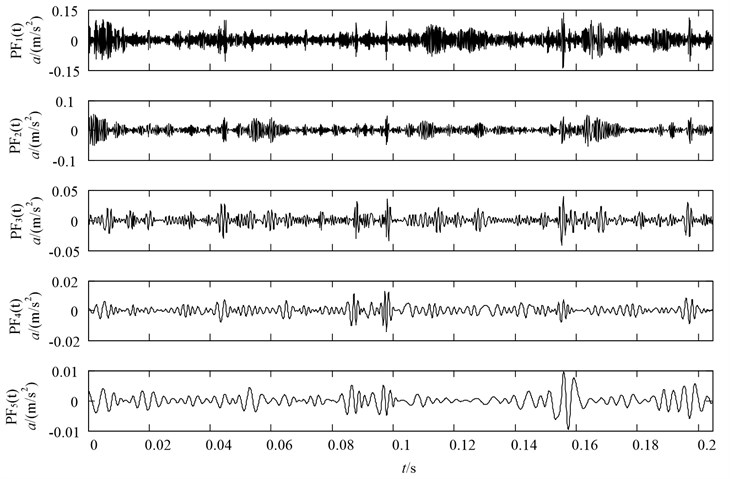
This implies the complexities of signals under the above three fault conditions are similar and the simply performing the PE of original signal cannot distinguish them effectively. Therefore, there remains a need for a denoising method to enhance the fault characteristics. Secondly, PF-PE values of fault working conditions are all higher than that of normal conditions. It is because that when the gearbox operates with local defect, it would appear periodical impulses with high frequency, hence, the complex degree of PF-PE values will increase. Thirdly, although the gearbox with different working conditions has different PF-PE values, they represent the similar trend, which consists well with real working condition of gearbox. Lastly, it can be observed from Fig. 14 that the front five PF-PE values exhibit higher distinguishability than the others, it is the reason that the front five PFs contains the main fault information.
Apparently, in this experiment, the front five features with most important information of the vibration signal are selected to form the new feature vectors. Naturally, the new feature vectors are used to train the ELM and then the test data set is applied to validate the recognition accuracy of ELM. According to the description in Table 2, 80 samples are randomly selected as training data, and the residual 80 samples are taken as testing data.
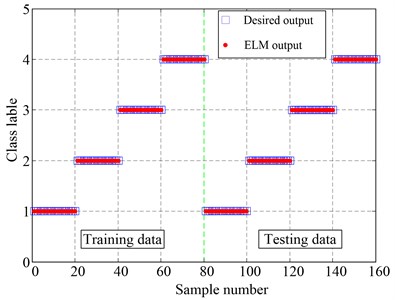
The experiment is repeated 10 times and the average classification results of the proposed method are shown in Fig. 15, which include the ELM outputs and the desired outputs about the training and testing samples. As can be seen, there are no training and testing samples misclassified and the average recognition accuracy reaches to 100 %. The comparison results demonstrate that the new proposed approach performs a good classification result, which is exactly suitable and effective in gear fault diagnosis.
Fig. 14Comparisons of PE and PF-PE of gearbox with different working conditions
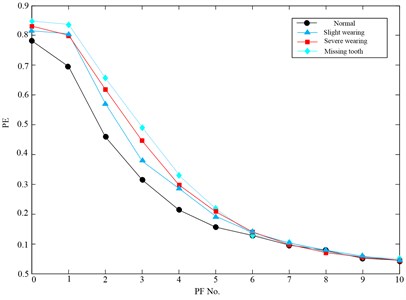
Fig. 15Classification results of the proposed method
For comparison purpose, the sample entropy (SE) method is also used to analyze the gear data [9], and the fault features obtained by PF-SE are also fed into ELM for pattern identification. Note that only the first five PFs are selected to calculate the SE values for comparison. Through the same process which includes the number of training and testing samples and the parameter selection of ELM, the classification results based on PF-SE and ELM are shown in Table 3. It can be easily found that one sample with slight wearing, one sample with severe wearing fault as well as three samples with missing tooth fault are misclassified. The total testing classification accuracy is 93.75 %, while the testing classification accuracy of PF-PE is 100 %. The comparisons demonstrate the fault features extracted using PF-PE method can better describe the characteristics of vibration signal, which has higher reparability than that of PF-SE method. Thus, PF-PE has a prominent advantage over PF-SE in terms of feature extraction under variable conditions of gearbox.
Table 3The classification results of the ELM classifier using PF-SE
Fault class | Class label | Number of training samples | The number of misclassified samples | Number of testing samples | The number of misclassified samples | Training accuracies/testing accuracies (%) |
Normal | 1 | 20 | 0 | 20 | 0 | 100/100 |
Slight wearing | 2 | 20 | 0 | 20 | 1 | 100/95 |
Severe wearing | 3 | 20 | 0 | 20 | 1 | 100/95 |
Missing tooth | 6 | 20 | 0 | 20 | 3 | 100/85 |
In total | 80 | 0 | 80 | 5 | 100/93.75 |
Back Propagation (BP) and support vector machine (SVM) are widely used in the classification, so a comparison among ELM, SVM and BP is conducted to validate the advantages of ELM. Besides, the training and testing data are the same in each algorithm. The classification accuracy and consuming time of each classifier using PF-PE as feature extractor are summarized in Table 4.
Through comparing the classification results, we can draw the conclusions that ELM has the highest accuracy and the least consuming time among three classifiers, it reinforces the superiority of the ELM in classification performance. Moreover, the comparison results show that the proposed PF-PE combined with ELM has outstanding performance in fault diagnosis of gearbox, which can be applied to recognize the different categories of gears.
Table 4Classification accuracy of each algorithm using PF-PE as feature extractor
Classifiers | Number of training samples | The number of misclassified samples | Number of testing samples | The number of misclassified samples | Training accuracies/testing accuracies (%) | Consuming time (s) |
BP | 80 | 0 | 80 | 0 | 100/100 | 4.76 |
SVM | 80 | 0 | 80 | 3 | 100/96.25 | 1.43 |
ELM | 80 | 0 | 80 | 5 | 100/9.75 | 0.69 |
In order to illustrate the potential application of proposed methodology, a comparative study between the present work and published literature presented in Table 5 [5, 26-29]. The comparing items include the machine elements used, fault severity levels, feature extraction method and classifier used, classified states, maximum classification efficiencies and denoising technique.
Table 5Comparisons between the current work and some published work
References | Machine element | Fault severity levels | Feature extraction method and classifier used | Classified states | Maximum classification efficiency | Denoising. technique |
Wu et al. (2012) [26] | Bearings | single | MPE and SVM | 4 | 100 % | NA |
Vakharia et al. (2014) [27] | Bearings | single | Different attribute filters and SVM, ANN | 4 | 97.5 % | Wavelet denoising |
Liu et al. (2014) [28] | Bearings | single | MSE and SVM | 4 | 100 % | LMD denoising |
Li et al. (2015) [5] | Bearings | single | MPE and SVM | 4 | 100 % | LMD denoising |
Yang et al. (2015) [29] | Gearbox | single | Kernel function and SVM | 3 | 94.67 % | EEMD denoising |
Wei et al. (Present work) | Gearbox | Multiple | PF-PE and ELM | 4 | 100 % | LMD denoising |
Note: MPE is multiscale permutation entropy, ANN is artificial neural network, LCD is local characteristic-scale decomposition and LMD is local mean decomposition | ||||||
6. Conclusions
A gearbox fault diagnosis method based on local mean decomposition (LMD), permutation entropy (PE) and extreme learning machine (ELM) is proposed in this paper. The fault signal is successfully preprocessed and decomposed into a number of product functions (PFs) by LMD. Then, the PE values of the first 5 PFs are calculated to generate the feature vector. Lastly, ELM is used to classify the states of gearbox, and the discussion result shows that ELM is superior to SVM and BP regarded as effective methods in the running time and classifying accuracy. The actual experimental data analysis demonstrates that the proposed LMD, PE and ELM approach is suitable and effective in gearbox diagnosis. Moreover, it is mentioned that the proposed method is promising, which is not limited to gearbox fault diagnosis but can be applied in fault diagnosis of other mechanical equipment.
References
-
Lee S. K., White P. R. Higher-order time-frequency analysis and its application to fault detection in rotating machinery. Mechanical Systems and Signal Processing, Vol. 11, Issue 4, 1997, p. 637-650.
-
Yang D., Liu Y., Li S., et al. Gear fault diagnosis based on support vector machine optimized by artificial bee colony algorithm. Mechanism and Machine Theory, Vol. 90, 2015, p. 219-229.
-
Peng Z. K., Peter W. T., Chu F. L. A comparison study of improved Hilbert-Huang transform and wavelet transform: application to fault diagnosis for rolling bearing. Mechanical systems and signal processing, Vol. 19, Issue 5, 2005, p. 974-988.
-
Wang Z., Lu C., Wang Z., et al. Health assessment of rotary machinery based on integrated feature selection and Gaussian mixed model. Journal of Vibroengineering, Vol. 16, Issue 4, 2014, p. 1753-1762.
-
Li Y., Xu M., Wei Y., et al. A new rolling bearing fault diagnosis method based on multiscale permutation entropy and improved support vector machine based binary tree. Measurement, Vol. 77, 2016, p. 80-94.
-
Sun J., Xiao Q., Wen J., et al. Natural gas leak location with K-L divergence-based adaptive selection of ensemble local mean decomposition components and high-order ambiguity function. Journal of Sound and Vibration, Vol. 347, 2015, p. 232-245.
-
Smith J. S. The local mean decomposition and its application to EEG perception data. Journal of the Royal Society Interface, Vol. 2, Issue 5, 2005, p. 443-454.
-
Yan R., Gao R. X. Approximate entropy as a diagnostic tool for machine health monitoring. Mechanical Systems and Signal Processing, Vol. 21, Issue 2, 2007, p. 824-839.
-
Zhang L., Xiong G., Liu H., et al. Bearing fault diagnosis using multi-scale entropy and adaptive neuro-fuzzy inference. Expert Systems with Applications, Vol. 37, Issue 8, 2010, p. 6077-6085.
-
Richman J. S., Moorman J. R. Physiological time-series analysis using approximate entropy and sample entropy. American Journal of Physiology-Heart and Circulatory Physiology, Vol. 278, Issue 6, 2000, p. 2039-2049.
-
Bandt C., Pompe B. Permutation entropy: a natural complexity measure for time series. Physical Review Letters, Vol. 88, Issue 17, 2002, p. 174102.
-
Bandt C., Keller G., Pompe B. Entropy of interval maps via permutations. Nonlinearity, Vol. 15, Issue 5, 2002, p. 1595-1602.
-
Bruzzo A. A., Gesierich B., Santi M., et al. Permutation entropy to detect vigilance changes and preictal states from scalp EEG in epileptic patients. A preliminary study. Neurological Sciences, Vol. 29, Issue 1, 2008, p. 3-9.
-
Li X., Ouyang G., Richards D. A. Predictability analysis of absence seizures with permutation entropy. Epilepsy Research, Vol. 77, Issue 1, 2007, p. 70-74.
-
Zunino L., Zanin M., Tabak B. M., et al. Forbidden patterns, permutation entropy and stock market inefficiency. Physica A: Statistical Mechanics and its Applications, Vol. 388, Issue 14, 2009, p. 2854-2864.
-
Nair U., Krishna B. M., Namboothiri V. N. N., et al. Permutation entropy based real-time chatter detection using audio signal in turning process. The International Journal of Advanced Manufacturing Technology, Vol. 46, Issues 1-4, 2010, p. 61-68.
-
Liu X., Gao C., Li P. A comparative analysis of support vector machines and extreme learning machines. Neural Networks, Vol. 33, 2012, p. 58-66.
-
Huang G. B., Zhou H., Ding X., et al. Extreme learning machine for regression and multiclass classification. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, Vol. 42, Issue 2, 2012, p. 513-529.
-
Bandt C., Pompe B. Permutation entropy: a natural complexity measure for time series. Physical Review Letters, Vol. 88, 2002, p. 17-174102.
-
Cao Y., Tung W., Gao J. B., et al. Detecting dynamical changes in time series using the permutation entropy. Physical Review E, Vol. 70, 2004, p. 4-46217.
-
Li Y., Xu M., Wei Y., et al. A new rolling bearing fault diagnosis method based on multiscale permutation entropy and improved support vector machine based binary tree. Measurement, Vol. 77, 2016, p. 80-94.
-
Huang G. B., Zhu Q. Y., Siew C. K. Extreme learning machine: a new learning scheme of feedforward neural networks. Proceedings of IEEE International Joint Conference on Neural Networks, Vol. 2, 2004, p. 985-990.
-
Huang G. B., Zhu Q. Y., Siew C. K. Extreme learning machine: theory and applications. Neurocomputing, Vol. 70, Issue 1, 2006, p. 489-501.
-
Li Y., Xu M., Haiyang Z. A new rotating machinery fault diagnosis method based on improved local mean decomposition. Digital Signal Processing, Vol. 46, 2015, p. 201-214.
-
Zhang X., Liang Y., Zhou J. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM. Measurement, Vol. 69, 2015, p. 164-179.
-
SWu D., Wu P. H., Wu C. W., Ding J. J., Wang C. C. Bearing fault diagnosis based on multiscale permutation entropy and support vector machine. Entropy, Vol. 14, 2012, p. 1343-1356.
-
Vakharia V., Gupta V. K., Kankar P. K. A multiscale entropy based approach to select wavelet for fault diagnosis of ball bearings. Journal of Vibration and Control, 2014, p. 1-9.
-
Liu H., Han M. A fault diagnosis method based on local mean decomposition and multi-scale entropy for roller bearings. Mechanism and Machine Theory, Vol. 75, 2014, p. 67-78.
-
Yang D., Liu Y., Li S., et al. Gear fault diagnosis based on support vector machine optimized by artificial bee colony algorithm. Mechanism and Machine Theory, Vol. 90, 2015, p. 219-229.
Cited by
About this article
The research is supported by National Natural Science Foundation of China (No. 11172078) and Important National Basic Research Program of China (973 Program-2012CB720003), and the authors are grateful to all the reviewers and the editor for their valuable comments.
