Abstract
A linear single degree-of-freedom (SDOF) oscillator with fractional-order PID controller of acceleration feedback is investigated by the averaging method, and the approximately analytical solution is obtained. Moreover, the numerical solution of the system is obtained by the step-down order method and the power series method progressively. The effects of the parameters in fractional-order PID controller on the dynamical properties are characterized by some new equivalent parameters. The proportional component of fractional-order PID controller is characterized in the form of equivalent mass. The integral component of fractional-order PID controller is denoted in the form of the equivalent linear damping and equivalent mass. The differential component of fractional-order PID controller is denoted in the form of the equivalent linear negative damping and equivalent mass. Those equivalent parameters could distinctly illustrate the effects of the parameters in fractional PID controller on the dynamical response. A comparison between the analytical solution with the numerical results is made, and their satisfactory agreement verifies the correctness of the approximately analytical results. The effects of the parameters in fractional-order PID controller on control performance are further analyzed by some performance parameters of the time response. Finally, the robustness of the fractional-order PID controller based on acceleration feedback is demonstrated through the control of a SDOF quarter vehicle suspension model.
1. Introduction
Fractional-order calculus includes the fractional-order integration and fractional-order differentiation, which is a natural generalization of traditional integer-order counterpart. The fractional-order calculus theory and numerical methods have made great progress in recent years [1-7]. Since many engineering problems can be described by fractional-order differential or integral equations, the application of fractional-order calculus in engineering is becoming more and more extensive. One of the important aspects is to add fractional-order feedback in the controlled system to improve the control performance, where the advantages of good robustness and strong anti-noise ability with fractional-order feedback are considered. For example, Chen et al. [8] studied the influence of fractional-order damping on the dynamic characteristics of van der Pol system. Song et al. [9] addressed the robust consensus problem of fractional-order linear multi-agent systems with positive real uncertainty. Wu et al. [10] studied the application of fractional-order calculus in the control of semi-active air suspension. Zeng et al. [11] applied fractional-order control to a fish processing machine and evaluated the performance through physical experiment.
PID (Proportional Integral Derivative) controllers are the most popular controllers used in industry because of their simplicity, performance robustness, and the availability of many effective and simple tuning methods based on minimum plant model knowledge. Podlubny [12] extended the traditional integer-order PID controller to the fractional-order counterpart. Compared with the traditional integer-order PID controller, the fractional-order PID controller has great advantages in stability and dynamic performance. At present, the research on fractional-order PID controller was mainly focused on the design method, stability analysis and parameters optimization of the controller [13-19].
Due to the application of acceleration feedback control is very extensive [20-24], a linear single degree-of-freedom (SDOF) oscillator with fractional-order PID controller of acceleration feedback is studied in this paper. The paper is organized as follow. Based on the averaging method, Section 2 presents the approximately analytical solution of the SDOF oscillator with fractional-order PID controller of acceleration feedback, where the equivalent linear damping, equivalent linear negative damping and three equivalent mass parameters are defined. These five equivalent parameters could completely reveal the effects of the coefficients and the orders in fractional-order PID controller on convergence speed and frequency characteristic of the approximate solution. In Section 3 the numerical solution of the system is obtained by the step-down order method and the power series method progressively. And the comparison between the analytical and numerical solution is presented. In Section 4, the effects of the coefficients and the orders in fractional-order PID controller on system control performance are further analyzed by some performance parameters of the time response. In Section 5, the parameter tuning process of fractional-order PID is demonstrated through the control of a SDOF quarter vehicle suspension model. In the vehicle suspension model, the fractional-order integral controller is arranged in the negative feedback loop, and the fractional-order PD controller is arranged in the positive feedback loop. The main conclusions are drawn at last.
2. Approximately analytical solution
The mathematical model for fractional-order PID controller in time domain is:
where and are the output and input for controller respectively. , and are the proportional constant, integration constant and differentiation constant respectively. and are the orders of fractional-order integral and differential component respectively. Fractional-order calculus is a generalization of integer-order integration and differentiation to non-integer order with fundamental operator . And the -order continuous operator is defined as:
where could be a real number, and is the upper bound of the integral operation.
Supposing that a fractional-order PID controller is arranged in the negative feedback loop, the considered SDOF oscillator with fractional-order PID controller of acceleration feedback is shown as:
where is the mass, is the linear stiffness, and is the linear damping. The initial values are generally considered as and . The fractional orders are restricted as and . The necessity, advantage, and realization methods of fractional-order PID controller could be found in [12] and other references. There are many definitions about fractional-order derivative, and the Caputo’s definition is adopted here. Then the fractional-order components of Eq. (3) are defined as:
where is Gamma function satisfying .
Eq. (3) can be transformed into:
where:
Then Eq. (6) could be solved by averaging method.
The solution for Eq. (6) could be supposed as:
where . Based on the averaging method, one could obtain the standard equations:
where:
The amplitude and the phase are the same small order variables as , and they change slower than . Accordingly, one could obtain the approximate forms of the amplitude and the phase in certain time interval. From the averaging method [25], one could select the time terminal as when 1, 2, 3) is periodic function, or when 1, 2, 3) is aperiodic one. Expanding the integrals, one could obtain another form of Eq. (8a):
where:
In order to calculate Eq. (10b) and Eq. (10c), some important results about the definite integrals in references [26-27] are presented as:
Then one could obtain:
Accordingly, one can get:
Similarly, one could get the simplified result about generalized phase as:
Furthermore, the amplitude and the phase are solved as:
Substituting the original system parameters into Eq. (15), one can get:
where the five new equivalent parameters are defined as:
where .
Accordingly, the approximately analytical solution for the SDOF oscillator with fractional-order PID controller of acceleration feedback could be established as:
From Eq. (18) it could be found that increases the damping of Eq. (3) so that is defined as the equivalent damping. decreases the damping of Eq. (3) and it could be defined as the equivalent negative damping. Moreover, , and will increase the mass of Eq. (3), and decrease the natural frequency of Eq. (3), so that , and are all defined as the equivalent masses. The effects of the fractional-order PID controller on the dynamical properties of SDOF oscillator could be summarized as follow.
1) The proportional component of fractional-order PID controller could increase the mass and reduce the natural frequency of the system.
2) The integral component of fractional-order PID controller would increase the damping and limit the amplitude of the system by , and decrease the natural frequency of the system by .
3) The differential component of fractional-order PID controller would decrease the damping and increase the amplitude of the system by , and decrease the natural frequency of the system by .
From Eq. (17), it could also be found that the function of fractional-order PID controller is not only related to the feedback of the system, but also on the coefficients , , and the orders and . That is listed here.
1) The proportional component of fractional-order PID controller regulates the mass and the natural frequency of the system by .
2) The integral component of fractional-order PID controller affects the dynamic characteristics of the system by and . When , the integral component degrades as linear mass , and decreases the natural frequency of the system by . When changes from 0 to 1, the integral component will gradually degrade into linear damping. When , the integral component degrades into linear damping .
3) The differential component of fractional-order PID controller affects the dynamic characteristics of the system by and . When , the differential component degrades into linear mass , and decreases the natural frequency of the system by . When changes from 0 to 1, the differential component gradually changes into linear negative damping. When , the differential component degrades into linear negative damping, and decreases the damping of the system by .
Supposing that the fractional-order PID controller is arranged in the positive feedback loop, the effect of fractional-order PID controller on the dynamic characteristics will be reversed, which will yield the negation of the equivalent parameters. This conclusion is easy to verify.
3. Comparisons between the approximate analytical solution and numerical solution
An illustrative example is studied herein as defined by the system parameters: –1, 5, 10, and Based on the approximately analytical solution as Eq. (18), one could analytically obtain the time history of the displacement for Eq. (3) denoted by the solid line shown in Fig. 1.
Fig. 1Comparison between the approximate analytical solution and numerical solution
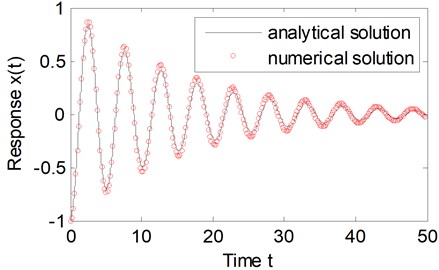
In order to verify the precision of the approximately analytical solution, we also present the numerical results. The relationship to the explicit numerical approximation of the power series method in reference [1-2] is:
where is the sample points, is the sample step, and is the binomial coefficient with the iterative relationship as:
However, we can’t directly use the power series method for Eq. (3). Because the fractional-order differentiation and integration are linear operations:
Eq. (3) can be transformed into:
by step-down order.
According to Eqs. (19), (20) and (22), the numerical scheme for Eq. (3) can be shown as:
For , one could obtain:
If , one should use:
Here we select 0.001. And the initial values for the fractional-order terms could be roughly selected as [27]:
As a comparison, the time history by numerical solution is also shown in Fig. 1 by the circles. From the observation of Fig. 1, it could be concluded that the approximately analytical solution agrees very well with the numerical results.
4. Analysis of the control performance
In this section, we will study the effects on system control performance of the coefficients , and and the orders and in fractional-order PID controller. The effects of fractional-order PID controller parameters on the rise time and peak value of system will be emphatically analyzed.
4.1. Rise time
The rise time which is the time for the system response curve to reach the steady-state amplitude. Based on Eq. (18), one could get:
In order to get the simplified form, another two equivalent parameters are defined, i.e. the equivalent negative stiffness and . The effects on system dynamics of the equivalent negative stiffness and equivalent mass are consistent, which can be proved by the following method. By using the Taylor series expansion one could obtain:
where and and is a variable.
Letting be the equivalent mass of system and , be the equivalent stiffness of system and , be the equivalent natural frequency of system and , from Eqs. (25) and (26) one could obtain:
Obviously, the rise time of system is related with the stiffness and the equivalent mass. The rise time will become longer with the increase of . The fractional-order PID controller will be changed into the traditional integer-order counterpart when and . And the rise time will remain unchanged with the change of and . Conversely, when and , the rise time will last longer with the increase of or .
In order to analyze the effect of the fractional orders more intuitively, other two parameters are fixed as 1 and 1. Henceforth we shall adopt the same initial value, except the parameter is specified as a variable. If the fractional order in integral component is changed from 0 to 1, one could obtain the equivalent natural frequency curve which is shown as Fig. 2. It could be found that the equivalent natural frequency tends to become larger with the increase of . Then the rise time will become shorter with the increase of .
Fig. 2Equivalent natural frequency curve with λ
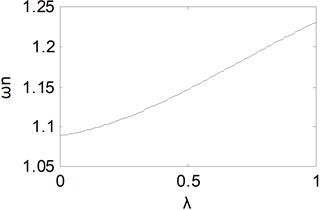
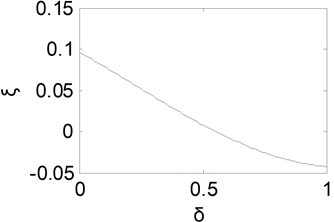
Fig. 3Equivalent natural frequency curve with δ
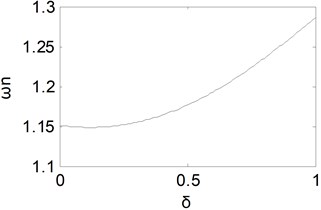
When the fractional order in differential component is changed from 0 to 1, one could obtain the equivalent natural frequency curve shown as Fig. 3. It could be found that the equivalent natural frequency remains almost unchanged for small and then tends to become larger with the increase of . Then the rise time will remain approximately invariant at first and then become shorter with the increase of .
4.2. Peak value
The time of peak value is the time for the system response curve to reach the first peak amplitude. From Eq. (18), one could get:
After expanding and simplifying Eq. (28), one could obtain:
Then, one could get:
Substituting Eq. (30) into Eq. (18), the peak value could be obtained as:
where and . Here is defined as the equivalent linear damping of system, and is defined as the equivalent damping ratio. Apparently, the peak value will become smaller with the increase of .
The peak value will become larger with the increase of . When the integral component coefficient is changed from 0 to 8, one could obtain the equivalent damping ratio curve of the fractional-order PID controller, which is shown in Fig. 4 by solid line. At the same time, the equivalent damping ratio curve of the traditional integer-order PID counterpart is shown by dotted line. From Fig. 4, it could be found that the equivalent damping ratio becomes larger with the increase of . The peak values of the two kinds of controllers will be almost the same at the beginning stage, and then the peak value of the fractional-order PID controller will be smaller than the traditional integer-order counterpart.
If the differential component coefficient is changed from 0 to 5, one could obtain the equivalent damping ratio curve of the fractional-order PID controller, which is shown in Fig. 5 by solid line. Meanwhile, the equivalent damping ratio curve of the traditional integer-order PID counterpart is shown by dotted line. From Fig. 5, it could be found that the equivalent damping ratios become progressively smaller with the increase of The peak values of the fractional-order PID controller will be smaller than the traditional integer-order counterpart at the beginning stage, and then it will be larger than the traditional integer-order counterpart. Obviously, when , the system will be unstable.
If the fractional order in integral component is changed from 0 to 1, one could obtain the equivalent damping ratio curve, which is shown in Fig. 6. From Fig. 6, it can be observed that the equivalent damping ratio will increase to the maximum and then decrease slightly. Therefore, the peak value will decrease to the minimum and then increase slightly.
When the fractional order in differential component is changed from 0 to 1, one could obtain the equivalent damping ratio curve, which is shown in Fig. 7. From Fig. 7, it could be found that the equivalent damping ratio become smaller progressively with the increase of . Accordingly, the peak value will become larger with the increase of .
Fig. 4Equivalent damping ratio curves with Ki
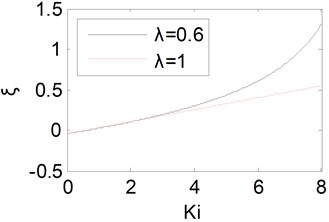
Fig. 5Equivalent damping ratio curves with Kd
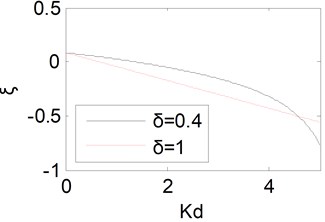
Fig. 6Equivalent damping ratio curve with λ
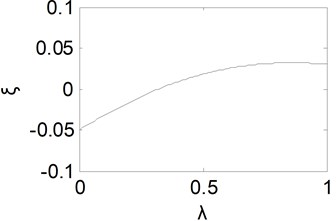
Fig. 7Equivalent damping ratio curve with δ
5. Control example
When designing a closed-loop control system, one should determine the type of feedback and then select the components of controller and tune parameters according to the control objectives, so as to improve the control performance. The vehicle suspension could be simplified to a SDOF control system under some assumptions. Next, we will study the active control of a SDOF quarter vehicle suspension model by fractional-order PID controller with acceleration feedback.
The selected basic system parameters are , , , , and one can get the damping ratio and the natural frequency . A well-designed vehicle suspension should provide isolation by reducing forces transmitted from vehicle axle to vehicle body [28]. In order to improve the ride comfort and guarantee a certain rapidity of the dynamic response, the control objectives are designed for that, the damping ratio , and the rise time remain unchanged, when the sprung mass is changed to .
Through the analysis of Section 4, one should arrange the fractional-order integral controller in the negative feedback loop, and arrange the fractional-order PD controller in the positive feedback loop.
According to the control objectives of system, one could get:
Solving Eq. (32), one can obtain infinite sets of solutions. For convenience of calculations, one could let , , and , then obtain a set of solutions, which is , and . The time histories of the vibration displacements before and after control are shown in Fig. 8. Obviously, the rise time of the system response is guaranteed, and the peak value is reduced, when the system is under the fractional-order PID control. The results show that, the fractional-order PID controller can achieve the control demands.
Fig. 8Comparison of before and after control
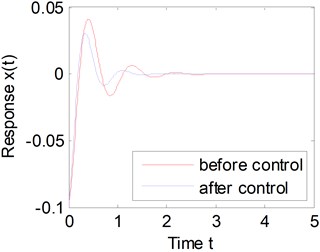
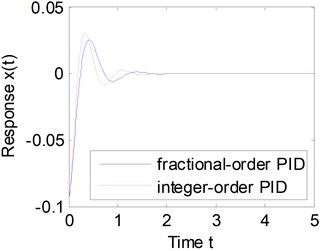
Fig. 9Comparison between fractional-order and integer-order PID controllers
Letting , , and , one could obtain another set of solutions, which is , , . The traditional integer-order PID controller can achieve the same control demands.
Next, the control performances are compared between the fractional-order PID and the traditional integer-order PID controller. When the stiffness of vehicle suspension is changed as , one could obtain the time histories of the vibration displacements with the PID controller of the above parameters, which are shown in Fig. 9. Apparently, the fractional-order PID controller has better robustness for the change of the stiffness.
6. Conclusions
A linear single degree-of-freedom oscillator with fractional-order PID controller of acceleration feedback is studied in this paper. The approximately analytical solution is obtained by the averaging method. The numerical solution is obtained by the step-down order method and the power series method. The accuracy of the method and the analytical results are demonstrated by comparison with the numerical solution. The effects of the parameters in fractional PID controller on the dynamical properties are characterized by equivalent linear damping, equivalent linear negative damping and three equivalent mass parameters. The effects of the parameters in fractional-order PID controller on system control performance are analyzed in detail by some performance parameters. Finally, the robustness of the fractional-order PID controller based on acceleration feedback is demonstrated through a control example. The research method and results may be helpful to the design of fractional-order PID controller of acceleration feedback, and provide a foundation for the control of free vibration with fractional-order PID controller.
References
-
Petras I. Fractional-Order Nonlinear Systems. Higher Education Press, Beijing, 2011.
-
Podlubny I. Fractional Differential Equations, Mathematics in Science and Engineering. Academic Press, New York, 1999.
-
Shen Y. J., Yang S. P., Xing H. J., et al. Primary resonance of Duffing oscillator with fractional- order derivative. Communication in Nonlinear Science and Numerical Simulation, Vol. 17, Issue 7, 2012, p. 3092-3100.
-
Rossikhin Y. A., Shitikova M. V. Application of fractional derivatives to the analysis of damped vibrations of viscoelastic single mass systems. Acta Mechanica, Vol. 120, Issues 1-4, 1997, p. 109-125.
-
Yang S. P., Shen Y. J. Recent advances in dynamics and control of hysteretic nonlinear systems. Chaos Solitons and Fractals, Vol. 40, Issue 4, 2009, p. 1808-1822.
-
Li C. P., Deng W. H. Remarks on fractional derivatives. Applied Mathematics and Computation, Vol. 187, Issue 1, 2007, p. 777-784.
-
Cao J. X., Ding H. F., Li C. P. Implicit difference schemes for fractional diffusion equations. Communication on Applied Mathematics and Computation, Vol. 40, Issue 4, 2013, p. 61-74.
-
Chen J. H., Chen W. C. Chaotic dynamics of the fractionally damped van der Pol equation. Chaos, Solitons and Fractals, Vol. 35, Issue 1, 2008, p. 188-198.
-
Song C., Cao J. D., Liu Y. Z. Robust consensus of fractional-order multi-agent systems with positive real uncertainty via second-order neighbors information. Neurocomputing, Vol. 165, 2015, p. 293-299.
-
Wu G. Q., Huang H. J., Ye G. H. Semi-active control of automotive air suspension based on fractional calculus. Transactions of the Chinese Society for Agricultural Machinery, Vol. 45, Issue 7, 2014, p. 19-24.
-
Zeng Q. S., De Silva L. W. The application of fractional order control in an industrial fish processing machine. Control and Intelligent Systems, Vol. 40, Issue 3, 2012, p. 177-185.
-
Podlubny I. Fractional-order systems and PID – controllers. IEEE Transactions on Automatic Control, Vol. 44, Issue 1, 1999, p. 208-214.
-
Zeng G. Q., Chen J., Dai Y. X., et al. Design of fractional order PID controller for automatic regulator voltage system based on multi-objective extremal optimization. Neurocomputing, Vol. 160, 2015, p. 173-184.
-
Zhong J. P., Li L. C. Tuning fractional-order (PID mu)-D-lambda controllers for a solid-core magnetic bearing system. IEEE Transactions on Control Systems Technology, Vol. 23, Issue 4, 2015, p. 1648-1656.
-
Chen Y. Q., Petras I., Xue D. Y. Fractional order control – a tutorial. American Control Conference Hyatt Regency Riverfront, St. Louis, MO, USA, 2009.
-
Saidi B., Amairi M., Najar S., et al. Bode shaping-based design methods of a fractional order PID controller for uncertain systems. Nonlinear Dynamics, Vol. 80, Issue 4, 2015, p. 1817-1838.
-
Chen L. C., Zhao L., Li W., et al. Bifurcation control of bounded noise excited Duffing oscillator by a weakly fractional-order PID feedback controller. Nonlinear Dynamics, Vol. 83, Issue 1, 2016, p. 529-539.
-
Chen L. C., Zhu W. Q. Stochastic jump and bifurcation of Duffing oscillator with fractional derivative damping under combined harmonic and white noise excitations. International Journal of Non-Linear Mechanics, Vol. 46, Issue 10, 2011, p. 1324-1329.
-
Chen L. C., Li Z. S., Zhuang Q. J., et al. First-passage failure of single-degree-of-freedom nonlinear oscillators with fractional derivative. Journal of Vibration and Control, Vol. 19, Issue 14, 2013, p. 2154-2163.
-
Wang Z. H., Zheng Y. G. The optimal form of the fractional-order difference feedbacks in enhancing the stability of a sDOF vibration system. Journal of Sound and Vibration, Vol. 326, Issues 3-5, 2009, p. 476-488.
-
Zhang T. M., Li G. T., Liang L. Switch variable structure control of a flexible manipulator with acceleration feedback. Chinese Journal of Mechanical Engineering, Vol. 38, Issue 3, 2002, p. 39-42.
-
Dumetz E., Dieulot J. Y., Barre P. J., et al. Control of an industrial robot using acceleration feedback. Journal of Intelligent and Robotic Systems: Theory and Applications, Vol. 46, Issue 2, 2006, p. 111-128.
-
Wang H. P., Li J., Zhang K. Sup-resonant response of a nonautonomous maglev system with delayed acceleration feedback control. IEEE Transactions on Magnetics, Vol. 44, Issue 10, 2008, p. 2338-2350.
-
An F., Chen W. D., Shao M. Q. Dynamic behavior of time-delayed acceleration feedback controller for active vibration control of flexible structures. Journal of Sound and Vibration, Vol. 333, Issue 20, 2014, p. 4789-4809.
-
Sanders J. A., Verhulst F., Murdock J. Averaging Methods in Nonlinear Dynamical Systems. Springer, New York, 2007.
-
Shen Y. J., Yang S. P., Xing H. J. Dynamical analysis of linear single degree-of-freedom oscillator with fractional-order derivative. Acta Phsysica Sinica, Vol. 61, Issue 11, 2012, p. 110505.
-
Shen Y. J., Yang S. P., Sui C. Y. Analysis on limit cycle of fractional-order van der Pol oscillator. Chaos, Solitons and Fractals, Vol. 67, 2014, p. 94-102.
-
Rajamani R. Vehicle Dynamics and Control. Springer, NewYork, 2012.
About this article
This work was financially supported by the National Natural Science Foundation of China (No. 11372198), the Cultivation Plan for Innovation Team and Leading Talent in Colleges and Universities of Hebei Province (No. LJRC018), the Higher Level Talents Scientific Research of Hebei Province (No. GCC2014053), and the High Level Talent of Hebei Province (No. A201401001).
