Abstract
In the paper a procedure for enhancement of noisy vibration signal for local damage detection is presented. The developed method is based on α-stable distribution approach. This distribution belongs to the rich class of heavy tailed family and was used in different applications. The proposed methodology covers decomposition of the signal via time-frequency spectrogram into set of narrowband sub-signals and estimation of stability parameter under the assumption that sub-signals constitute samples from α-stable distribution. As a result of sub-signals modelling, we obtain distribution of α parameter vs. frequencies that is analogy to spectral kurtosis approach well known in the literature. Such characteristic is basis for filter design used for raw signal enhancement. To evaluate efficiency of our method we compare raw and filtered signal in time, time-frequency and frequency (envelope spectrum) domains. The presented methodology we applied to real vibration signal from two stage heavy duty gearbox used in mining industry.
1. Introduction
Local damage detection in heavy-duty mechanical systems is currently one of the most explored and investigated field of the modern condition monitoring [1, 2]. Some of the methods in this field are based on the analysis of the signal in the time domain [3-8]. Most of them use impulsive character of the signal [9-11] or specific structure of envelope spectrum [12]. One of the approach exploits cyclostationarity behaviour of the vibration signal [13-15]. However, signal from machine with local damage is very non-stationary and have complex structure therefore here is need to apply more advanced techniques and analyse the signal in time-frequency domain [16-25].
In the literature for many proposed methods of local damage detection first the signal is decomposed [2-3] and then the further analysis is provided in order to extract its informative part. Most of the methods are based on the specific behaviour of the decomposed signal, like impulsiveness or its cyclic (or periodic) character observable especially in the sub-signals corresponding to the frequency bands of underlying signal after division of its frequency spectrum. In that cases the measures of impulsiveness (or periodicity) are applied to appropriate sub-signals and then the informative frequency bands are selected [10, 12, 26-28]. We only mention here methods based on the local maxima [29], sparsity [30-32] or statistical measures based on moments, quantiles, or cumulative distribution functions [28] and stochastic modelling techniques [33-39].
In this paper we propose a method of local damage detection that is based on the enhancement of noisy vibration signal. In the developed technique we use the α-stable distribution approach [37]. More precisely, we estimate the stability index for each sub-signal from time-frequency representation taking the assumption that it can be modelled by using α-stable distribution which is an extension of the classical Gaussian one [40]. In our approach we obtain distribution of the stability index versus frequency, that provides similar picture as spectral kurtosis well known in the literature. On the basis of the obtained characteristic we can design the filter in order to enhance of the raw signal. To evaluate efficiency of our method we compare raw filtered signal. This comparison we present in time, time-frequency and frequency (envelope spectrum) domains. The presented methodology we apply to real vibration signal from two stage heavy duty gearbox used in mining industry.
The paper is organized as follows. In Section 2 we present in details methodology related to -stable distribution modelling and procedure of filter design based on this approach. In Section 3 we analyse the real vibration signal in the context of the presented methodology. The last section contains conclusions.
2. Theoretical background
In this section we present the procedure of extraction of informative part of vibration signal. We provide here necessary definitions related to applied statistical methods and introduce novel technique that allows us to enhance informative frequency band in order to detect the local damage. We extend the classical methodology based on the spectral kurtosis [11] and propose to model the sub-signals corresponding to frequency bands in time-frequency representation (spectrogram) by using -stable (stable) distribution. This distribution is very often treated as a natural extension of the classical Gaussian one. Moreover it is worth mentioning, the stable distribution is especially important in the context of modelling of data with visible jumps however for specific values of stable distribution parameters it reduces to Gaussian one. As a result of sub-signals modelling, we obtain distribution of stability index with respect to frequencies. Such characteristic is basis for filter design used for raw signal enhancement.
In the first step of the introduced method the raw signal is transformed into the time-frequency map through the short-time Fourier transform (STFT) [41]:
where is the shifted window and is the input signal. Each sub-signal corresponding to appropriate frequencies can be treated as a time series. Since the STFT matrix is complex, absolute value needs to be taken in order to obtain the spectrogram. In the proposed procedure we assume the sub-signals corresponding to appropriate frequencies from the spectrogram constitute samples from -stable distribution. This is related to the fact that for sub-signals with impulsive behavior the stability parameter tends to be lower than for sub-signals without impulses and hence the parameter can be treated as a selector for informative frequency band selection. We mention, a random variable is an -stable distributed if its characteristic function takes the following form [42]:
where is stability parameter, is asymmetry parameter, is scale parameter and is location parameter. In our procedure by the assumption that the sub-signals are described by the -stable distribution, in the next step for each time series corresponding to appropriate frequencies we estimate the parameter [43]. In this paper we apply the regression method which is based on the characteristic function of the considered distribution (see Eq. (2)). After modelling of appropriate sub-signals by using stable distribution we obtain a set of parameters corresponding to frequencies. The next step of the procedure is to design the filter. The filter (-filter) is defined as follows:
where is the estimated parameter for sub-signal corresponding to frequency . At the end the signal is filtered and its main characteristics are analyzed.
3. Real data analysis
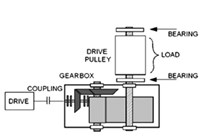
To prove efficiency of the proposed method we apply it to the real vibration signal from complex machine operating in the harsh environment in mining industry. Measurements have been performed using Bruel-Kjaer Pulse system with parameters of data acquisition as follows: length of the signal 2.5 s, sampling frequency equal to 8192 Hz and expected fault frequency equal to 4.1 Hz. The signals were acquired using an accelerometer located on the bearing’s housing in horizontal direction. The machine was normally loaded and the rotational speed was approximately constant during the data acquisition (Fig. 1).
Fig. 1a) – Scheme of the investigated machinery, b) – sensor location in gearbox case, c) – coupling between gearbox and pulley, d) – sensor location in pulley case
a)

b)

c)

d)
Fig. 2Waveform of acquired signal (top panel) with its envelope spectra (bottom panel)
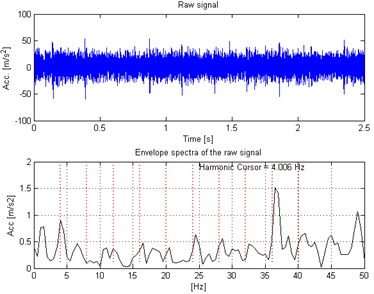
Fig. 3Spectrogram of the acquired signal
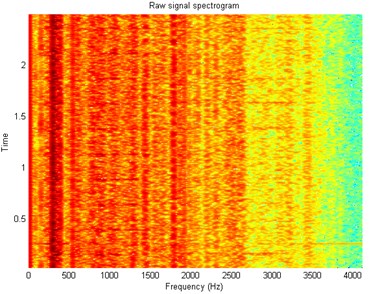
Fig. 4Filter characteristic based on the spectrogram frequency sub-signals
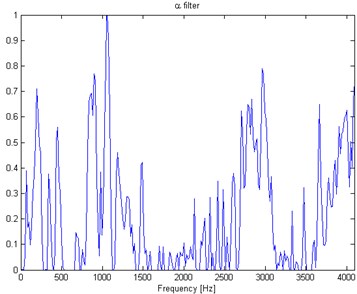
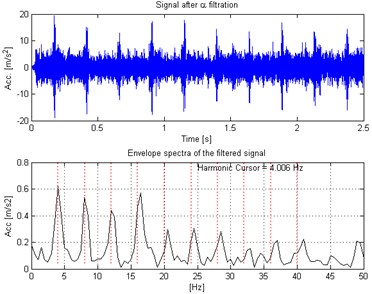
In Fig. 2 top panel the acquired vibration signal from the two-stage gearbox is presented in time domain. One can notice some impulses, but it cannot be concluded that they come from the damage. Furthermore, in the Fig. 2 bottom panel we present the envelope spectra of the signal. After performing visual inspection of the examined gearbox, it was found that damage is localized on the tooth in gear-wheel mounted on second (middle) shaft in the gearbox. Damage frequency is calculated with the machine kinematics and localized at 4.1 Hz. As one can see, it is hard to find harmonics of the fundamental frequency at envelope spectra of raw signal. This is the main reason to apply methodology for the enhancement of the impulses related to the fault. In Fig. 3 spectrogram of the raw signal is presented. We cannot easily select the informative frequency band. In Fig. 4, there is presented the -filter characteristics. While in Fig. 5 we show a time-frequency map of the signal after performing filtration. One can easily notice significant increase in energy for the impulses related to the fault. Furthermore, Fig. 6 contains the filtered signal (top panel) in time domain and envelope spectra (bottom panel). It can be denoted that the damage can be observable in time domain (visible cyclic impulses) as well as in envelope spectra. The fundamental frequency with transparent location of its harmonics we observe in both panels of Fig. 6.
Fig. 5Spectrogram of the α-filtered signal
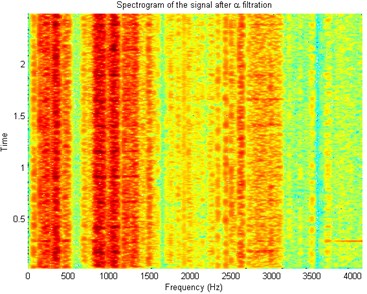
Fig. 6Waveform of the α-filtered signal (top panel) with its envelope spectra (bottom panel)
4. Conclusions
In the paper a novel method for filtering vibration signals is proposed. The filtering procedure was developed in order to enhance the raw vibration signal, i.e. improve its signal to noise ratio.
The approach is based on the fundamental property, meaning impulsivity in a certain frequency band indicating presence of the fault in the machine. The key problem is to identify these frequency band and create appropriate filter characteristic. For purpose of measuring impulsivity we adapted -stable distribution and its stability parameter . In the literature the -stable distribution is especially important in modeling of processes with impulsive character.
In the case of machine in the healthy condition, distribution of signal (and consequently each sub-signal for given frequency band) is close to the Gaussian which is particular case of the -stable distribution with parameter close to 2. For machines in the bad condition, impulsivity in the signal will affect many frequency bands (energy flow in that bands will reveal impulsive character, too). In consequence, stability parameter will become significantly smaller than 2.
Distribution of alpha parameter vs. frequency allows to indicate so called informative frequency band and might be used as filter characteristic. Application of the method for real vibration signals proved that both in time domain as well as in envelope spectrum signal reveals much clearly presence of damage. After filtering, in time domain cyclic impulses are more visible. Also in envelope spectrum one might notice fundamental frequency together with family of harmonics that is clear signature of local damage in gearbox.
References
-
Zimroz R. Role of signal preprocessing in local damage detection in mining machines. Diagnostyka, Vol. 2, Issue 46, 2008, p. 33-36.
-
Obuchowski J., Wylomańska A., Zimroz R. Recent developments in vibration based diagnostics of gear and bearings used in belt conveyors. Applied Mechanics and Materials, Vol. 683, 2014, p. 171-176.
-
Braun S. The synchronous (time domain) average revisited. Mechanical Systems and Signal Processing, Vol. 25, Issue 4, 2011, p. 1087-1102.
-
Chaturvedi G. K., Thomas D. W. Adaptive noise cancelling and condition monitoring. Journal of Sound and Vibration, Vol. 76, Issue 3, 1981, p. 391-405.
-
Lee S. K., White P. R. The enhancement of impulsive noise and vibration signals for fault detection in rotating and reciprocating machinery. Journal of Sound and Vibration, Vol. 217, Issue 3, 1998, p. 485-505.
-
Khemili I., Chuchane M. Detection of rolling element bearing defects by adaptive filtering. European Journal of Mechanics A/Solids, Vol. 24, 2005, p. 293-303.
-
Barszcz T. Decomposition of vibration signals into deterministic and nondeterministic components and its capabilities of fault detection and identification. International Journal of Applied Mathematics and Computer Science, Vol. 19, Issue 2, 2009, p. 327-335.
-
Zimroz R., Bartelmus W. Application of adaptive filtering for weak impulsive signal recovery for bearings local damage detection in complex mining mechanical systems working under condition of varying load. Solid State Phenomena, Vol. 180, 2012, p. 250-257.
-
Samuel P. D., Pines D. J. A review of vibration-based techniques for helicopter transmission diagnostics. Journal of Sound and Vibration, Vol. 282, Issues 1-2, 2005, p. 475-508.
-
Antoni J. Fast computation of the kurtogram for the detection of transient faults. Mechanical Systems and Signal Processing, Vol. 21, Issue 1, 2007, p. 108-124.
-
Randall R. B., Antoni J. Rolling element bearing diagnostics – a tutorial. Mechanical Systems and Signal Processing, Vol. 25, Issue 2, 2011, p. 485-520.
-
BarszczT.,JabłońskiA. A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kurtogram. Mechanical Systems and Signal Processing, Vol. 25, Issue 1, 2011, p. 431-451.
-
Raad A., Antoni J., Sidahmed M. Indicators of cyclostationarity: theory and application to gear fault monitoring. Mechanical Systems and Signal Processing, Vol. 22, Issue 3, 2008, p. 574-587.
-
Antoni J. Cyclostationarity by examples. Mechanical Systems and Signal Processing, Vol. 23, Issue 4, 2009, p. 987-1036.
-
Urbanek J., Antoni J., Barszcz T. Detection of signal component modulations using modulation intensity distribution. Mechanical Systems and Signal Processing, Vol. 28, 2012, p. 399-413.
-
Lei Y., Lin J., He Z., Zuo M. J. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mechanical Systems and Signal Processing, Vol. 35, Issues 1-2, 2013, p. 108-126.
-
Dybała J., Zimroz R. Rolling bearing diagnosing method based on empirical mode decomposition of machine vibration signal. Applied Acoustics, Vol. 77, 2014, p. 195-203.
-
Peng Z. K., Chu F. L. Application of the wavelet transform in machine condition monitoring and fault diagnostics: a review with bibliography. Mechanical Systems and Signal Processing, Vol. 18, Issue 2, 2004, p. 199-221.
-
Yan R., Gao R. X., Chen X. Wavelets for fault diagnosis of rotary machines: a review with applications. Signal Processing, Vol. 96A, 2014, p. 1-15.
-
Feng Z., Liang M., Chu F. Recent advances in time-frequency analysis methods for machinery fault diagnosis: a review with application examples. Mechanical Systems and Signal Processing, Vol. 38, Issue 1, 2013, p. 165-205.
-
Lin J., Zuo M. J. Gearbox fault diagnosis using adaptive wavelet filter. Mechanical Systems and Signal Processing, Vol. 17, Issue 6, 2003, p. 1259-1269.
-
Obuchowski J.,WyłomańskaA.,ZimrozR. The local maxima method for enhancement of time-frequency map and its application to local damage detection in rotating machines. Mechanical Systems and Signal Processing, Vol. 46, Issue 2, 2014, p. 389-405.
-
Urbanek J., Barszcz T., Antoni J. Time–frequency approach to extraction of selected second-order cyclostationary vibration components for varying operational conditions. Measurement, Vol. 46, Issue 4, 2013, p. 1454-1463.
-
Makowski R., Zimroz R. Parametric time-frequency map and its processing for local damage detection in rotating machinery. Key Engineering Materials, Vol. 588, 2014, p. 214-222.
-
Żak G., Obuchowski J., Wyłomańska A., Zimroz R. Novel 2D representation of vibration for local damage detection. Mining Science, Vol. 21, 2014, p. 105-113.
-
Li C., et al. Criterion fusion for spectral segmentation and its application to optimal demodulation of bearing vibration signals. Mechanical Systems and Signal Processing, 2015.
-
Antoni J., Randall R. B. The spectral kurtosis: Application to the vibratory surveillance and diagnostics of rotating machines. Mechanical Systems and Signal Processing, Vol. 20, Issue 2, 2006, p. 308-331.
-
Obuchowski J., Wyłomańska A., Zimroz R. Selection of informative frequency band in local damage detection in rotating machinery. Mechanical Systems and Signal Processing, Vol. 48, Issues 1-2, 2014, p. 138-152.
-
Obuchowski J.,WyłomańskaA.,ZimrozR. The local maxima method for enhancement of time-frequency map and its application to local damage detection in rotating machines. Mechanical Systems and Signal Processing, Vol. 46, Issue 2, 2014, p. 389-405.
-
Tse P. W., Wang D. The sparsogram: A new and effective method for extracting bearing fault features. Prognostics and System Health Management Conference, PHM-Shenzhen, 2011, p. 5939587.
-
Tse P. W., Wang D. The design of a new sparsogram for fast bearing fault diagnosis: Part 1 of the two related manuscripts that have a joint title as “two automatic vibration-based fault diagnostic methods using the novel sparsity measurement – Parts 1 and 2”. Mechanical Systems and Signal Processing, Vol. 40, Issue 2, 2013, p. 499-519.
-
Tse P. W., Wang D. The automatic selection of an optimal wavelet filter and its enhancement by the new sparsogram for bearing fault detection: Part 2 of the two related manuscripts that have a joint title as “two automatic vibration-based fault diagnostic methods using the novel sparsity measurement – Parts 1 and 2”. Mechanical Systems and Signal Processing, Vol. 40, Issue 2, 2013, p. 520-544.
-
Obuchowski J., Wyłomańska A., Zimroz R. Stochastic modeling of time series with application to local damage detection in rotating machinery. Key Engineering Materials, Vol. 569, 2013, p. 441-449.
-
Yu G., Li C., Zhang J. A new statistical modeling and detection method for rolling element bearing faults based on alpha-stable distribution. Mechanical Systems and Signal Processing, Vol. 41, Issues 1-2, 2013, p. 155-175.
-
Makowski R. A., Zimroz R. Adaptive bearings vibration modelling for diagnosis. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 6943 LNAI, 2011, p. 248-259.
-
Makowski R., Zimroz R. New techniques of local damage detection in machinery based on stochastic modelling using adaptive Schur filter. Applied Acoustics, Vol. 77, 2014, p. 130-137.
-
Żak G., Obuchowski J., Wylomańska A., Zimroz R. Application of ARMA modelling and alpha-stable distribution for local damage detection in bearings. Diagnostyka, Vol. 15, Issue 3, 2014, p. 3-10.
-
Obuchowski J., Wylomanska A., Zimroz R. Two-stage data driven filtering for local damage detection in presence of time varying signal to noise ratio. Mechanisms and Machine Science, Vol. 23, 2015, p. 401-410.
-
Wylomanska A., Zimroz R., Janczura J. Identification and stochastic modelling of sources in copper ore crusher vibrations. Journal of Physics: Conference Series Vol. 628, 2015, p. 012125.
-
Wyłomańska A., Chechkin A., Sokolov I. M., Gajda J. Codifference as a practical tool to measure interdependence. Physica A, Vol. 421, 2015, p. 412-429.
-
Allen J. B. Short term spectral analysis, synthesis, and modification by discrete Fourier transform. IEEE Transactions on Acoustics, Speech and Signal Processing, Vol. 25, Issue 3, 1977, p. 235-238.
-
Samorodnitsky G., Taqqu M. S. Stable Non-Gaussian Random Processes. Chapman and Hall, New York, 1994.
-
Burnecki K., Wyłomańska A., Beletskii A., Gonchar V., Chechkin A. Recognition of stable distribution with Levy index alpha close to 2. Physical Review E, Vol. 85, 2012, p. 056711.
About this article
This work is partially supported by the Statutory Grant S50112 (Radosław Zimroz), S50112 (Grzegorz Żak).
