Abstract
The current paper investigates the effect of Variable Friction System (VFS) on the response of Triple Friction Pendulum Bearing (TFPB) under normal and parallel components of near-fault ground motions. The Triple Variable Friction Pendulum Bearing (TVFPB), a developed TFPB, is proposed in this study. The variation of the frictional force on sliding surfaces of TVFPB is such that up to a certain value of displacement, the friction coefficient increases and then decreases with further increase in displacement. In order to verify the effectiveness of VFS, the analytical seismic responses are compared with the response of the same system supported on conventional TFPB. Based on the results, it can be concluded that the usage of VFS is quiet effective in reducing the displacement of isolation system. Moreover, by comparing the superstructure demands, it is observed that for stiff bearings with smaller displacement capacity, the incorporation of VFS will result in lower superstructure demands, whereas for flexible bearings with larger displacement capacity, superstructure demands are increased.
1. Introduction
Seismic Isolation is an effective solution for decoupling structures from potential earthquake damages by increasing the flexibility of the system and providing an appropriate damping ratio together with energy dissipation. This technology has been used with high efficiency in the design and retrofitting of important buildings, bridges, storage tanks and infrastructures [1, 2]. However, previous studies have shown that isolated structures are vulnerable to near-fault ground motions, especially the pulse-like motions. These excitations can impose significant demands, especially large isolator displacement, on the seismic responses of isolated structures, which can affect the feasibility of project [3].
The most practical way to overcome this problem is to add supplementary dampers across the isolation system to increase the damping ratio of system. The utilization of viscous supplementary dampers is effective for eliminating the displacement of the isolator, especially for mid-rise to high-rise buildings [4, 5]. However, analytical studies have shown that by using these dampers, the flexibility of seismic isolation is reduced and the demands in the superstructure are increased significantly, especially if the structure encounters a lower level motion [6, 7].
Another way to limit the effect of near-fault motions on isolated structures is based on optimizing the mechanical design parameters of isolation system, in order to produce the minimum levels of superstructure force and isolator displacement. There are many studies that by applying sensitive analysis optimum properties of lead rubber bearing (LRB) and friction pendulum system (FPS) or parametric equations to find the best properties, are provided for buildings and bridges under near-fault ground motions [8-10].
Recently, authors applied sensitive analysis on the properties of Triple Friction Pendulum Bearing (TFPB) by using 26 near-fault pulse-like (NF-Pulse) excitations and 23 non-pulse near-fault (NF-No Pulse) ground motions to find optimum values. Based on the results, the best performance of the isolation system is found when the TFPB works in its third stage of motion. Moreover, the optimum ranges for coefficient of friction and effective radius of curvature of all sliding surfaces are provided [3].
Besides optimizing conventional isolation systems, there are some studies on the response of isolator with varying parameters under near-fault motions. One of these systems is Variable Friction Pendulum System (VFPS), which the variation of the frictional force in this system is such that up to a certain value of displacement the coefficient of friction on sliding surface increases and then it decreases with further increase in displacement. By using such variable friction coefficient, the isolator displacement and base shear of structure decrease, yet the superstructure acceleration increases under near-fault ground motions [11, 12].
This study proposes a new type of TFPB named “Triple Variable Friction Pendulum Bearing” (TVFPB) in order to use the adaptive behavior of TFPB in achieving multiple performance objectives under multiple levels of hazard with the benefit of Variable Friction System (VFS) in eliminating isolator displacement under near-fault excitations. Herein, the response of stiff single story building isolated by the TVFPB is investigated under normal and parallel components of near-fault ground motions. The specific objectives of this research are (1) to study the performance of isolated structure with TVFPB by incorporating the bi-directional interaction effect of normal and parallel components of near-fault ground motions, (2) to compare the seismic response of isolated structure with TVFPB and conventional TFPB to measure the effectiveness of TVFPB, (3) to investigate the influence of important parameters, such as effective period, damping ratio and initial stiffness of isolation system, on the response of the isolated structure.
2. Triple variable friction pendulum bearing (TVFPB)
The conventional TFPB which was proposed by Fenz and Constantinou consists of four concave surfaces and three independent pendulum mechanisms. A section through a conventional TFPB is shown in Fig. 1. Referring to Fig. 1, the outer concave plates have effective radius and , and the friction coefficients of these interfaces are and . The articulated slider assembly consists of two concave slide plates separated by a rigid slider. The inner surfaces of the two slide plates have effective radius of and . The surfaces of both of these plates are coated with a non-metallic sliding material characterized by coefficients of friction and . The standard configuration of TFPB has large and equal effective radius for the outer concave plates and small and equal effective radius for the inner slide plates, i.e. . The coefficients of friction of sliding surfaces are selected so that the isolator exhibits high stiffness and low friction initially and subsequently decreases in stiffness and increases in effective friction as the amplitude of displacement increases, i.e. [13].
Fig. 1Section through a conventional TFPB
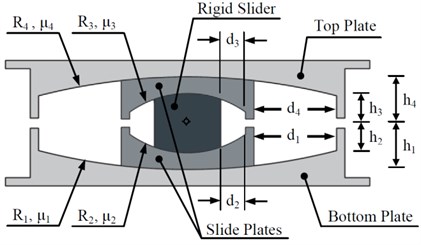
The new proposed bearing, TVFPB, is similar to the conventional TFPB. The difference between TVFPB and TFPB is that the friction coefficient of the sliding surfaces of TFPB are considered to be constant whereas the friction coefficient of the sliding surfaces of TVFPB are varied based on Eq. (1) which proposed by Panchal and Jangid [11] and its variation is illustrated in Fig. 2:
where is the initial value of friction coefficient on the th sliding surface, and are the parameters that describe the variation of friction coefficient on the th sliding surface, is the radial relative displacement on the th sliding surface, and are the relative displacements on the th sliding surface of the TVFPB in the - and -directions, respectively.
Fig. 2Comparison between friction coefficient of the sliding surfaces of TVFPB and TFPB
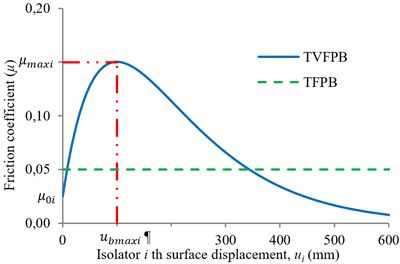
The curve is chosen such that up to a certain value of displacement the frictional force increases and then it decreases with further displacement. Such variation of friction coefficient can be achieved by varying the level of lubrication and roughness of spherical surface.
The value of index displacement, , of each sliding surface, which represent the initial stiffness of slider, is found out by maximizing the friction coefficient of each slider, and it is given by:
The parameters, and can be evaluated by using Eqs. (1) and (2) and selecting the initial value of the friction coefficient on th sliding surface and the index displacement of it.
3. Equations of motion
The hysteretic behavior of the TFPBs can be simulated by a series model of three independent single friction pendulum bearings (SFPB) which are connected by two slider masses (Fig. 3).
Fig. 3Idealized three SFPBs in series for modeling the TFPB
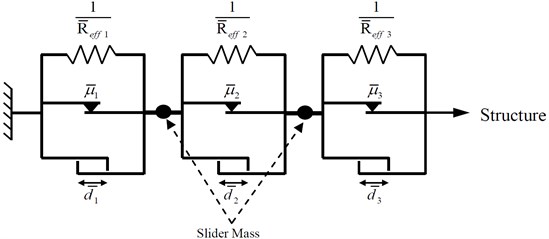
Each element in the series model is composed of a parallel arrangement of: (a) a linear spring with stiffness equal to , (b) a velocity-dependent perfectly plastic friction element represented by the modified Bouc-Wen model with the coefficient of friction equal to , and (c) a gap element with displacement capacity of . Therefore, the force produced by the th isolator element in the - and -direction are given by:
where is the mass supported by each isolator, and are the relative displacements of SFPB element in the - and -directions, is the radial relative displacement of SFPB element , is the stiffness after gap closing, which should be assigned a large value, and denotes the Heaviside function. and denote two dimensionless variables of th element along the - and -directions, respectivley. In the case of biaxial interaction they are governed by the following differential equations [1]:
where is the yield displacement; and , and are dimensionless quantities that control the shape of the hysteresis response, for which the recommended values are: 0.25 mm, 1, 0.9, and 1 [1].
The coefficient of friction at each sliding interface, , are based on the type of bearing. For conventional TFPB, the value of friction coefficient is constant, and for TVFPB the value of friction coefficient is calculated based on Eq. (1).
Since the variables change quite slowly when the bearing is sliding and very rapidly in the regions where the motion reverses the direction or when sticking occurs, the governing equations are systems of stiff differential equations. Therefore, to solve the system equations two operations should be conducted: first, the time step in the solution algorithm should have a very small value (5×10-3 sec has been found suitable), and second, a special algorithm for solving these types of equation should be used.
4. Numerical results
The effectiveness of VFS on the response of TFPB is evaluated by comparison of the results of nonlinear time history analysis (NLTHA) under selected near-field excitations. Six pairs of near-fault ground motions are used to evaluate the dynamic behavior of TVFPB under bi-directional excitation. These near-fault ground motions are the same as the records which were used to study the behavior of sing VFPS [11, 12]. This set of ground motions, which were downloaded from the PEER Strong Motion Database [14], covers the magnitude range of 6.5-7.3 and site-to-source distance lower than 16 km (Table 1). According to ASCE 7-10, site class for recording stations is classified as C (very dense soil and soft rock) or D (stiff soil).
For the present study, the response of a symmetric three-dimensional single-story building supported by four TFPB or TVFPB is investigated (Fig. 4, Table 2). This system is same as the one adopted in previous studies about modeling of the TFPB for response-history analysis [1, 15]. The period of the structure with fixed base is 0.2 sec and the superstructure damping ratio is assumed to be 0.25 %.
Table 1Properties of near-fault ground motions used in NLTHA
NGA seq. No. | Event | Year | Station | (km) | Site class | PGA (g) | ||
Normal | Parallel | |||||||
180 | Imperial Valley-06 | 1979 | El Centro Array #5 | 6.5 | 4 | D | 0.375 | 0.527 |
182 | Imperial Valley-06 | 1979 | El Centro Array #7 | 6.5 | 0.6 | D | 0.462 | 0.335 |
879 | Landers | 1992 | Lucerne | 7.3 | 2.2 | C | 0.717 | 0.797 |
1004 | Northridge-01 | 1994 | LA - Sepulveda VA | 6.7 | 8.4 | C | 0.731 | 0.707 |
1063 | Northridge-01 | 1994 | Rinaldi Receiving Station | 6.7 | 6.5 | D | 0.870 | 0.424 |
1085 | Northridge-01 | 1994 | Sylmar, Converter Sta. East | 6.7 | 5.2 | C | 0.839 | 0.495 |
Table 2Properties of stiff single-story building supported on TFPB [1, 15]
Section property | Area (mm2) | Moment of inertia (mm4) | Torsion constant (mm4) | Shear Area (mm2) | Mass (kg) | Weight (kN) |
Column (C) | 5.0 × 106 | 6.851 × 107 | 1.0 × 108 | 5.0 × 106 | 0 | 0 |
Beam (B) | 5.0 × 106 | 1.0 × 1011 | 1.0 × 108 | 5.0 × 106 | 0 | 0 |
Fig. 4Properties of stiff single-story building supported on TFPB [1, 15]
![Properties of stiff single-story building supported on TFPB [1, 15]](https://static-01.extrica.com/articles/16280/16280-img4.jpg)
To consider the effect of bearing flexibility, the responses for three different geometrical configurations (effective radius and displacement capacity) are investigated (Table 3). Based on this, GC3 exhibits a comparatively stiff isolator with small displacement capacity, GC5 exhibits a comparatively soft isolator with large displacement capacity and specification of GC4 is somewhat placed between the GC3 and GC5. In all NLTHA to eliminate the effect of impact to final restrainer, the displacement capacity of inner sliding surfaces assumed to be infinite.
Table 3Geometry configuration of bearings used
Designation | Displacement capacities (mm) | Effective radius (mm) | |||
GC3 | 90 | 300 | 780 NL | 450 | 2250 |
GC4 | 120 | 400 | 1040 NL | 600 | 3000 |
GC5 | 150 | 500 | 1300 NL | 750 | 3750 |
Also, the effect of isolator damping ratio is studied by considering four different sets of friction coefficients used for each geometrical configuration, which in the case of TFPB is shown in Table 4. In the case of TVFPB, the initial value of friction coefficient, , is considered as the maximum value of 0.01 and , and the maximum value of friction coefficient, , is considered as tree times the friction coefficient of TFPB, i.e. .
Moreover, to evaluate the effect of initial stiffness of TVFPB, the value of index displacement, , of each sliding surface is considered to be equal to 25 %, 75 % and 100 % of displacement capacity of the surface in each case of analysis.
The equations of motion of system is derived based on Section 4, and these 22 first order ordinary differential equations are solved simultaneously by using the ode15s solver in MATLAB. The ode15s solver is a variable order, multi-step algorithm which is quite effective for solving the systems of stiff differential equations [16].
Table 4Friction coefficient values of surfaces in the case of TFPB
Designation | ||||
LF1 | 0.01 | 0.02 | 0.03 | 1:2:3 |
LF2 | 0.01 | 0.03 | 0.06 | 1:3:6 |
HF1 | 0.02 | 0.04 | 0.06 | 1:2:3 |
HF2 | 0.02 | 0.04 | 0.08 | 1:2:4 |
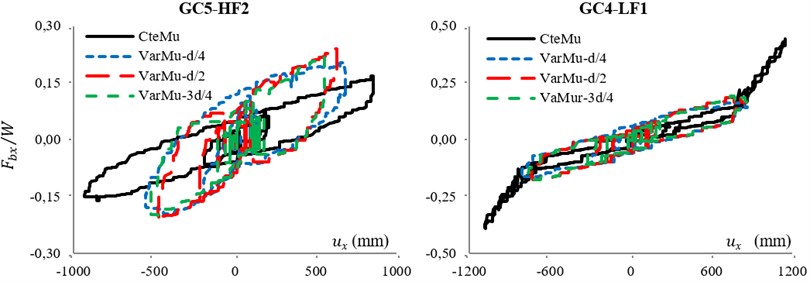
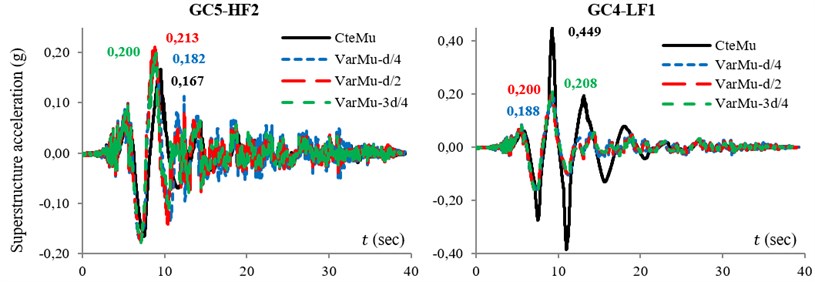
The responses of GC4-LF1 and GC5-HF2 for 1979 Imperial Valley-06 (El Centro Array #5) are shown in Fig. 5. The hysteresis loop of conventional TFPB (with constant friction coefficient: CteMu) with the response of TVFPB (with variable friction coefficient: VarMu) in three cases of index displacement, , and time histories of superstructure acceleration for -direction of structure under normal component of near-fault excitations are shown in this figure.
Fig. 5Response of system under IVA5: a) hysteresis loop of isolators, b) variation of superstructure acceleration
a)
b)
The figure depicts that because of the type of friction coefficient of TVFPB, the area of hysteresis loop of TVFPB in smaller displacement is equal to the area of hysteresis loop of conventional TFPB. Also the maximum bearing displacement in the case of TVFPB is about 30 % smaller than TFPB displacement.
Moreover, it is concluded that when bearings are working at their final stage, e.g. GC4-LF1, the utilization of VFS is effective in reducing superstructure demand. However, when bearings are working at their soft or semi-stiff stage, e.g. GC5-HF2, by using VFS the demand of structure will increase slightly.
To study the overall response of the TVFPB and TFPB, the average of peak seismic demands are evaluated. The seismic demands considered in this study are: (a) peak orthogonal isolator displacement, (b) base shear of structure, (c) maximum inter-story drift of the superstructure, and (d) superstructure acceleration. To illustrate the variation of superstructure demands, a Superstructure Demand Function (SDF) based on the Eq. (6) is defined.
Fig. 6Variation of bearing displacement and SDF against index displacement under near-fault motions
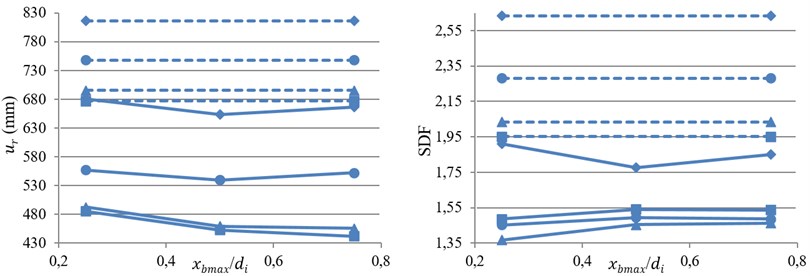
a) GC3
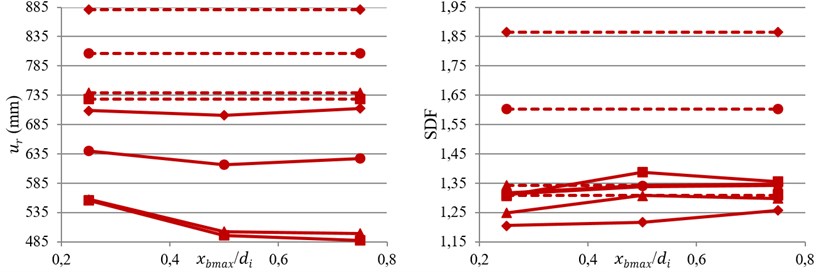
b) GC4
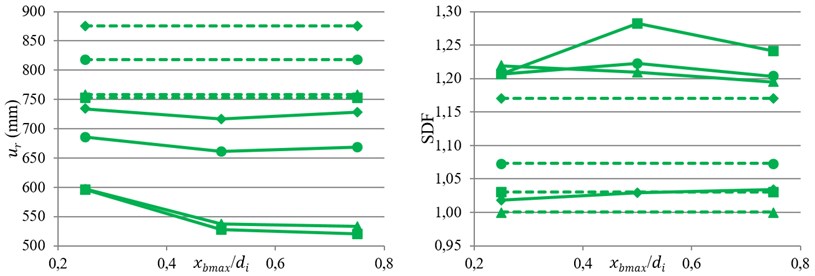
c) GC5

According to this Eq. (6), the lower the value of SDF, the better performance of the bearing on the structural response:
where is the top floor absolute acceleration of the structure, is the maximum inter-story drift of the superstructure, is the base shear of structure, min() is the minimum value of variable from the analyses, is an index to indentify the th TFPB configuration, and denotes the weight of each single objective function that indicates the importance factor of each single function; the summation of values should be equal to unity (). The importance factor of each single objective function is considered equal, thus .
The averages of the bearing displacement and SDF from near-fault records against index displacement, , are shown in Fig. 6. According to bearing displacement results, by increasing the flexibility of bearing, the effect of VFS on eliminating bearing displacement is reduced. Based on the results it can be conclude that the average of bearing displacement for GC3, GC4 and GC5 in the case of TVFPB is about 0.72, 0.75 and 0.78 of TFPB, respectively.
Moreover, for bearings with small friction coefficient, LF1 and LF2, by increasing the value of , bearing displacement first decreases and then increases with further increase of . On the contrary, for bearings with larger friction coefficient, HF1 and HF2, decreasing the initial stiffness of isolator (increasing ) up to a certain value will reduce bearing displacement, and after that it does not affect it anymore.
Based on SDF results it can be concluded that for stiff isolators with relative small displacement capacity, e.g. GC3, the value of SDF is reduced by using VFS. However, by increasing the flexibility and displacement capacity of bearing, GC5, the value of SDF is increased with utilization of VFS.
Also, for TVFPB increasing the value of friction coefficient will increase the SDF, which is not observed in conventional TFPB. Moreover, by increasing the value of , the value of SDF first increased and then a little decreased with further increase of .
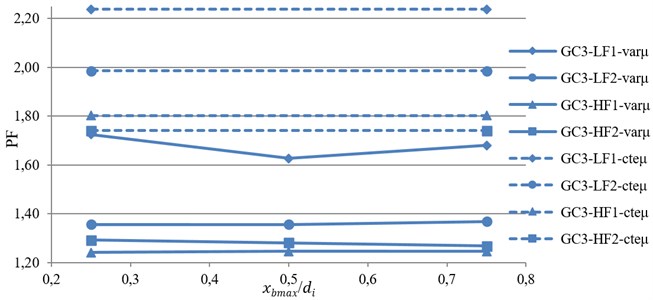
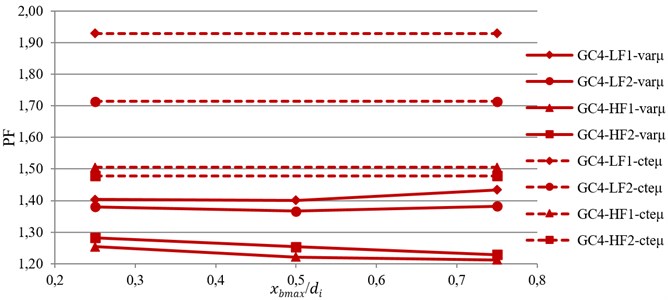
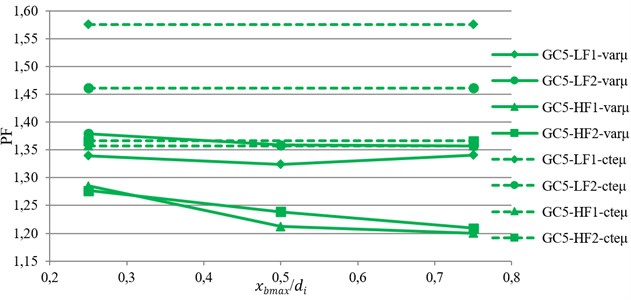
Finally, to compare the overall response of the TVFPB and TFPB, a Performance Function (PF) that considers all the seismic responses simultaneously, are evaluated based on Eq. (7):
where is the performance function, , , , have been defined previously, is the isolator displacement. Because of the importance of under near-fault motions and the aim of using base isolation in eliminating superstructure demands, the importance factor of SDF is considered to be equal to that of the isolator displacement and so .
The variation of average value of the PF against index displacement, , is shown in Fig. 7. From this figure, it can be concluded that by using VFS the value of PF is reduced and so the performance of bearing is improved. This improvement is reduced by decreasing the stiffness and increasing the displacement capacity of bearing.
Moreover, for isolators with low friction coefficient, e.g. LF1 and LF2, by increasing the value of , the value of PF first decreased and then increased with further increase of . However, for isolators with high friction coefficient, e.g. HF1 and HF2, decreasing the initial stiffness of isolator (increasing ) will reduce PF and so the performance of TVFPB is improved. Therefore, the optimum value of , is equal to the half of the displacement capacity of sliding surfaces.
Based on the results, it can be concluded that the usage of VFS is quiet effective in reducing the displacement of TFPB isolation system. Moreover, by comparing the superstructure demands, it is observed that for stiff bearings with smaller displacement capacity, the incorporation of VFS will result in lower superstructure demands, whereas for flexible bearings with larger displacement capacity, superstructure demands are increased. Therefore, the VFS is quite effective for improving the seismic performance of isolated structures supported on TFPB under near-fault ground motions.
Fig. 7Variation of performance function against index displacement under near-fault motions
5. Conclusions
The analytical seismic response of Triple Variable Friction Pendulum Bearing (TVFPB) is investigated under normal and parallel components of near-fault ground motions. The variation of the frictional force on sliding surfaces of TVFPB is such that up to a certain value of displacement, the friction coefficient increases and then decreases with further increase in displacement.
In order to verify the effectiveness of Variable Friction System (VFS), the analytical seismic responses are compared with the response of the same system supported on conventional Triple Friction Pendulum Bearing (TFPB). The criterion selected for verifying the effectiveness is based on minimizing both the bearing displacement and Superstructure Demand Function (SDF) simultaneously, which is defined as Performance Function (PF). The results of the study can be summarized as follows:
1) With supporting building by TVFPB, the demands of superstructure and isolator displacement during near-fault ground motions can be controlled within a desirable range without much alteration to top floor absolute acceleration.
2) By using VFS the displacement TFPB can be reduced up to 30 %, which is quite effective in reducing the cost of project.
3) For stiff TFPB with small displacement capacity, the usage of VFS will decrease SDF, however SDF is increased for flexible TFPB with larger displacement capacity.
4) By using VFS the value of PF is reduced which results in improvement of the performance of bearing. This improvement is reduced by decreasing the stiffness and increasing the displacement capacity of bearing.
5) The optimum value of index displacement, the displacement which the value of friction coefficient is maximized, to optimize the total performance of TVFPB is equal to the half displacement capacity of sliding surfaces.
6) With the usage of VFS, the lateral seismic force required to fully activate the isolation system is reduced so the design codes’ limit on minimum design shear force of building is reduced which results in a more cost effective building.
References
-
Ghodrati Amiri G., Namiranian P. Evaluation of capacity spectrum method in estimating seismic demands of triple pendulum bearings under near-field ground motions. International Journal of Structural Stability and Dynamics, Vol. 14, Issue 2, 2014, p. 20.
-
Han Qiang, Wen Jianian, Du Xiuli Nonlinear response of continuous girder bridges with isolation bearings under bi‑directional ground motions. Journal of Vibroengineering, Vol. 17, Issue 2, 2015, p. 816-826.
-
Ghodrati Amiri G., Namiranian P., Shamekhi Amiri M. Seismic response of triple friction pendulum bearing under near-fault ground motions. International Journal of Structural Stability and Dynamics, Vol. 16, 2016, p. 32.
-
Calugaru V., Panagiotou M. Seismic response of 20-story base-isolated and fixed-base reinforced concrete structural wall buildings at a near-fault site. Earthquake Engineering and Structural Dynamics, Vol. 43, Issue 6, 2014, p. 927-948.
-
Wolff E. D., Ipek C., Constantinou M. C., Tapan M. Effect of viscous damping devices on the response of seismically isolated structures. Earthquake Engineering and Structural Dynamics, Vol. 44, Issue 2, 2015, p. 185-198.
-
Kelly J. M. The role of damping in seismic isolation. Earthquake Engineering and Structural Dynamics, Vol. 28, Issue 1, 199, p. 3-20.
-
Providakis C. P. Effect of supplemental damping on LRB and FPS seismic isolators under near-fault ground motions. Soil Dynamics and Earthquake Engineering, Vol. 29, Issue 1, 2009, p. 80-90.
-
Jangid R. S. Optimum friction pendulum system for near-fault motions. Engineering Structures, Vol. 27, Issue 3, 2005, p. 349-359.
-
Jangid R. S. Optimum lead–rubber isolation bearings for near-fault motions. Engineering Structures, Vol. 29, Issue 10, 2007, p. 2503-2513.
-
Karalar M., Padgett J. E., Dicleli M. Parametric analysis of optimum isolator properties for bridges susceptible to near-fault ground motions. Engineering Structures, Vol. 40, 2012, p. 276-287.
-
Panchal V. R., Jangid R. S. Variable friction pendulum system for near-fault ground motions. Structural Control and Health Monitoring, Vol. 15, 2008, p. 568-584.
-
Panchal V. R., Jangid R. S. Seismic response of structures with variable friction pendulum system. Journal of Earthquake Engineering, Vol. 13, 2009, p. 193-216.
-
Fenz D. M., Constantinou M. C. Development, Implementation and Verification of Dynamic Analysis Models for Multi-Spherical Sliding Bearings. Technical Report MCEER-08-0018, Multidisciplinary Center for Earthquake Engineering Research, University at Buffalo, State University of New York, Buffalo, NY, 2008.
-
Pacific Earthquake Engineering Research Strong Ground Motion Database. http://peer.berkeley.edu/ngawest2/, 2010.
-
Fenz D. M., Constantinou M. C. Modeling triple friction pendulum bearings for response-history analysis. Earthquake Spectra, Vol. 24, Issue 4, 2008, p. 1011-1028.
-
MATLAB Reference Guide. Math Works Inc., 2009.
