Abstract
This work presents a method for predicting vibration at any location along the span of a pipeline using a model constructed from experimental data. The hybrid approach involves the construction of an initial model using system identification techniques of experimental data, and a modified model using Linear Quadratic Estimator (LQE) and Linear Quadratic Regulator (LQR) approach. The combination of the two approaches resulted in a system that is capable of predicting vibration at random locations along the span of the pipe section using minimal feedback from physical system. Change in vibration signature at any location on the pipeline can be used as an early warning against damage at that location. The proposed method can be utilized as a practical damage detection technique of underground pipelines and buried structures. The validity of the propose approach has been examined experimentally and the results are presented.
1. Introduction
Research on vibration-based damage detection is increasingly gaining momentum due to factors like economic and technical advantages. The basic principle is that modal parameters such as natural frequencies, mode shapes and modal damping are functions of the system’s physical properties namely, mass, damping, and stiffness. Hence, changes in physical properties manifest itself as changes in modal properties which depend on the nature, location and severity of the damage [1]. Therefore, damages can be quantified from changes in modal frequencies and mode shapes.
At the initial stage, an accurate dynamic model of the system under study is needed to predict its dynamic response over time. However, in some situations, structures to be tested or diagnosed are not accessible for measurements, and/or modeling conditions are not properly identified or too complex to model. Examples of such models are, underground pipelines, subsea tunnels and pipelines and underground foundations. These and similar situations, present a modelling challenge where obtaining a working model can be tedious and time consuming. Therefore, system identification is an effective and practical approach to build a dynamic model. System identification is a black box method which is based on experimental data only. In this approach, there are no prior requirements and assumptions related to structural parameters, properties and boundary conditions [2]. Generically, system identification techniques use the method of least square fit to identify system parameters. They can be classified into two categories: deterministic and statistical, where both can be used to identify system parameters, such as a damping and modal frequencies of the system [3].
Chang, Baek [4] obtained a baseline structure first using FEM and then modified it using SI to get the related perturbations. Mastorocostas and Theocharis [5] introduced a kind of fuzzy neural model for dynamic system identification. The recurrent models are similar as closed loop systems whose feedback paths introduce dynamics to the model. This model can learn the system dynamics without any basic knowledge about the structure of the system. Chen, Kurt [6] performed a method about nonlinear system identification which is used for structural health monitoring and damage detection based on measured acceleration signals. The method used in this research is presented in the following sections.
2. System modelling
2.1. System identification methodology and procedures
System identification of vibrating system is to develop a parametrized model based on measured excitation and/or response signals. In this work, an instrumented hammer is used to provide the input impulse force while accelerometers measure the response at different locations on the pipe span. System identification toolbox in MATLAB is utilized to obtain and initial model from raw experimental data. General identification procedure is outlined in Fig. 1.
Fig. 1General identification procedure

In this work, many types of models were test and validated against experimental data and the Box-Jenkins model which belongs to polynomial model class is found to have the best performance. The principle formula of Box-Jenkins model class is shown below:
where represents the output; represents the input and represents the error predicted. Models with various best fits can be obtained when the parameters , , , are adjusted [7-9]. The polynomial model generated is converted to discrete state-space format such that the dynamic system of the pipeline is:
where quadruple represents the state-space model obtained using system identification toolbox.
2.2. Construction of the hybrid model
The hybrid model presented in this work uses the initial state-space model from system identification shown in Eq. (2) and the LQE and LQR techniques to generate optimal estimates of the system’s states such that the associated cost functions are minimized. The generic form of the cost function is for LQR is:
where and represent the states and control inputs, respectively. The choice of and depends on the transient response and measurement qualities [7-10]. The hybrid model is shown in Fig. 3.
3. Experimental and simulation results
The experimental setup is shown Fig. 2 in which Accelerometers (a) is located at the right side of the pipe section, (b) is at the middle and (c) is at the left. An instrumented hammer applies the excitation force at the right end of the pipe. DSpace and its data acquisition system measures hammer force as well as the accelerometers’ responses and utilize them in a hardware-in-the-loop format in as shown in Fig. 3, to produce an optimal estimate of pipe vibration at any desired location. It is worth mentioning that, in this experimental work, only one accelerometer measurement is used to update the model (i.e., feedback signal), the remaining accelerometers are used for comparison with estimates at corresponding locations.
Fig. 2Experimental setup

Fig. 3Schematic of the hybrid model
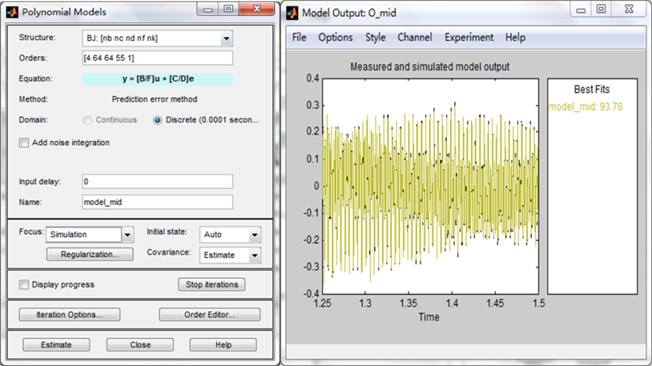
Fig. 4 show the system identification (SysID) main window, and the model match to experimental results. It is also worth mentioning that 70 % of the data points are used to construct the model while the remaining 30 % are used for SysID model verification.
Fig. 4Constructing model based on Box-Jenkins model
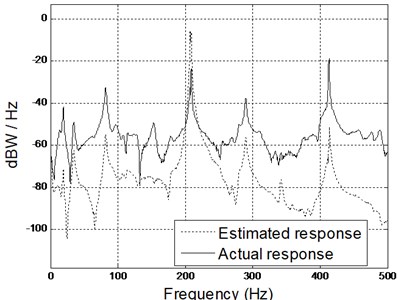
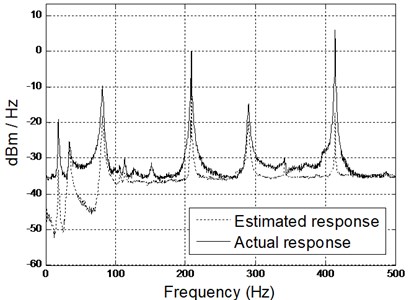
Comparison between estimated response and actual response using only SysID model, in frequency domain, are showed in Fig. 5 (solid line is actual response and dashed line is estimated). It is clear that the SysID model poorly predicts the actual vibration of the pipeline at the corresponding locations.
Fig. 5Comparison of spectrogram between estimated and actual results (middle and right accelerometers) using SysID model
a)
b)
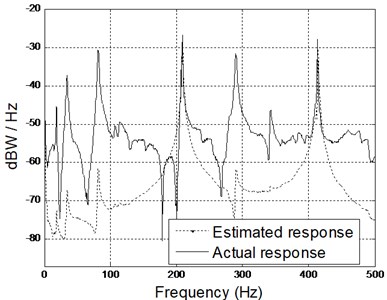
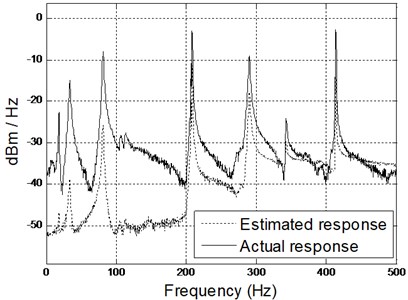
However, implementing the hybrid model approach shows that the model is capable of predicting the vibration fairly accurately with minimal discrepancies and exact resonant frequencies match as shown in Fig. 6. The amplitude scaling is related to hardware bias.
Fig. 6Comparison of spectrogram between estimated and actual results (middle and right accelerometers) using hybrid model
4. Conclusions
In this work, a novel approach for predicting vibration of a buried pipeline or structures is presented. An initial system identification model is constructed from impulse response data of the structure. The initial model is then improved in a hybrid approach format such that, an optimal estimator is constructed and actual measurement are used to improve estimates of the structural vibration at desired location. The number of actual measurements needed to update the initial model is kept at minimal to mimic real-life applications where few measurements of the structural vibration can be afforded. The hybrid approach improved the model significantly and the integrity of the model is verified experimentally. The model succeeded in predicting the vibration at any location of choice with good accuracy.
References
-
Doebling S. W., Farrar C. R., Prime M. B. A summary review of vibration-based damage identification methods. Shock and Vibration Digest, Vol. 30, Issue 2, 1998, p. 91-105.
-
Le Ber L., et al. IDENT 1D – a novel software tool for an easy identification of material constitutive parameters. Nuclear Engineering and Design, Vol. 186, Issue 3, 1998, p. 343-352.
-
Jovanović O. Identification of dynamic system using neural network. The Scientific Journal Facta Universitatis Series: Architecture and Civil Engineering, Vol. 31, 1997, p. 525-532.
-
Chang S., et al. Structural system identification using degree of freedom-based reduction and hierarchical clustering algorithm. Journal of Sound and Vibration, 2015.
-
Mastorocostas P., Theocharis J. B. A recurrent fuzzy-neural model for dynamic system identification. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, Vol. 32, Issue 2, 2002, p. 176-190.
-
Chen H., et al. Experimental system identification of the dynamics of a vibro-impact beam with a view towards structural health monitoring and damage detection. Mechanical Systems and Signal Processing, Vol. 46, Issue 1, 2014, p. 91-113.
-
Ljung L. System Identification Toolbox for Use with MATLAB. 2007.
-
Fassois S. Identification, Model Based Methods. Academic Press, 2001, p. 673-686.
-
Ljung L. System Identification Toolbox: User’s Guide. Citeseer, 1995.
-
Lewis F. L., D. L. Vrabie, V. L. Syrmos Optimal Control of Discrete – Time Systems. Optimal Control, Third Edition, 1986, p. 19-109.
About this article
Authors acknowledge the support of the Petroleum Institute.
