Abstract
The analytical solutions of hygrothermal effects in heterogeneous piezoelectric solid and hollow cylinders are obtained. The interaction of electric displacement, electric potentials, and elastic deformations is discussed. The present cylinder is subjected to a mechanical load at its lateral surfaces as well as an electric potential. The displacement, stresses and electric potentials in the heterogeneous piezoelectric cylinders are determined. The material properties coefficients of the present cylinder are assumed to be changed in the radial direction. The hygrothermoelastic responses of piezoelectric heterogeneous hollow and solid circular cylinders are presented. Numerical application examples for both cylinders are displayed. The significant of influence of material inhomogeneity, initial temperature, final moisture, and the pressure load and electric potential ratios are investigated. Suitable discussions and conclusions are presented.
1. Introduction
Recently, the hygrothermal analysis of different composite structures has been the subject of research interest. The changes in the temperature and moisture concentration may be appeared according the change of the environmental (heat and wet) conditions. The thermal effect is due to the effect of temperature while the hygroscopic effect is due to the moisture absorption from the atmosphere. However, a combination of both effects may be occurs and it is known as the hygrothermal effect. This effect may induce a dimensional change in the structure and as a result, the deformation conditions will be induced to get what so called the residual stresses.
Several works that restricted for the hygrothermal responses of cylindrical structures have been published in the literature. Some of them are concerned with the thermoelastic analysis [1-6] while the other is concerned with the different responses of cylindrical structures in hygrothermal environments [7-9]. It is to be noted, from now, that the piezoelectric materials have been widely used in many industrial applications due to the special electromechanical coupling effects. Many theoretical investigations have been reported in the analysis for thermo-piezoelectric solid and hollow cylinders. Wang [10] has obtained the transient thermal fracture of a piezoelectric cylinder. Dai et al. [11] have studied the thermo-electro-elastic behaviors in piezoelectric hollow cylinders subjected to thermal shock and electric excitation. Dai and Wang [12] have investigated the magneto-thermo-electro-elastic transient analysis in piezoelectric hollow cylinders. Arani et al. [13] have presented the semi-analytical solution of electro-thermo-mechanical creep for radially polarized piezoelectric cylinder.
The effects due to inhomogeneity as well as the hygrothermal parameters on the piezoelectric cylinders are rarely investigated. Dai et al. [14] have presented the electro-magneto-elastic behaviors for the functionally graded piezoelectric solid cylinder and sphere. Fesharaki et al. [15] have developed the general theoretical analysis for a functionally graded piezoelectric hollow cylinder subjected to 2-D electromechanical load. Zenkour [16] has presented the piezoelectric analysis of thermally-gradient inhomogeneous hollow cylinders. Arefi [17] has investigated the effects of thermal, mechanical, and electrical loads on the nonlinear behavior of a functionally graded piezoelectric cylinder. Dai and Jiang [18] have studied the electro-magneto-thermo-elastic analysis of a FG piezoelectric solid cylinder. Allam et al. [19] have studied the effects of different parameters on FG piezoelectric cylinders in hygrothermal environment conditions. Recently, Zenkour [20, 21] has presented the hygrothermoelastic responses of piezoelectric hollow cylinders.
In this investigation, both ambient temperature and moisture concentration are assumed to have variable distributions through the radial direction of the present cylinders. The material properties like elastic coefficients, piezoelectric parameters, dielectric parameter, and pyroelectric coefficients are all assumed functions of the radial direction of the cylinder. The hygrothermoelastic responses of the inhomogeneous piezoelectric hollow and solid circular cylinders are presented. Numerical results of the field quantities are presented and the effects of various parameters are investigated.
2. Basic equations of hygrothermoelastic piezoelectric cylinders
Consider a long inhomogeneous circular cylinder having perfect conductivity. The present cylinder may be solid of radius or hollow of inner radius and outer radius . The hollow circular cylinder is subjected to internal and external pressures and , respectively. However, the solid circular cylinder is subjected to an external pressure . Let the cylindrical coordinates of any representative point be and assume that the cylinder is subjected to radically changing of temperature and moisture concentration . For the axisymmetric plane strain assumption, the components of radial displacement; radial, hoop, and axial stresses; and radial electric displacement and electric potential may be expressed as , , and , respectively.
2.1. Constitutive equations
The constitutive relations are:
where are the elastic coefficients, are the piezoelectric parameters, is the dielectric parameter, and and are the pyroelectric coefficients. Also, and are the stress-temperature moduli and humidity expansion coefficients of the present inhomogeneous cylinder. That is:
where and are the thermal and moisture expansion coefficients.
2.2. Heat equation
The temperature distribution through the radial direction of the cylinder is governed by the heat conduction equation [11]:
where is the heat generation function and represents the thermal conductivity.
2.3. Moisture equation
In modeling, the transient moisture diffusion equation is analogous to the transient heat conduction equation. It can be described by the following equation [11]:
where the moisture diffusivity coefficient.
2.4. Equilibrium equation
The equilibrium equation for the inhomogeneous piezoelectric hollow or circular cylinder, in the absence of body forces, is expressed as:
2.5. Charge equation of electrostatics
In the absence of free charge density, the charge equation of electrostatics for both cylinders is expressed as:
2.6. Boundary conditions for a hollow cylinder
The boundary conditions for temperature are:
where is the reference initial temperature.
The boundary conditions for the moisture concentration are:
where is the reference final moisture concentration.
In addition, the mechanical and electric boundary conditions are expressed as:
where and are the internal and external pressures, respectively while and are the internal and external electric potentials, respectively.
2.7. Boundary conditions for a solid cylinder
The temperature, moisture concentration, mechanical and electric boundary conditions of the solid cylinder are given, respectively, by:
where and are the reference initial temperature and final moisture concentration. However, and denote the external pressure and the external electric potential.
3. Closed-form solutions
The closed-form exact solutions for the inhomogeneous piezoelectric hollow and solid circular cylinders are given by solving all of the temperature, moisture, and equilibrium equations. The solutions are completed by application of the mechanical, electric, temperature, and moisture boundary conditions.
3.1. Closed-form solution for a hollow circular cylinder
Let the coefficients , , , , , , and are changed through the radial direction of the present hollow circular cylinder according to the relations:
where is an inhomogeneity geometric parameter and , , , , , , and represent the corresponding properties of the homogeneous hollow circular cylinder. The value equals zero represents a fully homogeneous cylinder. The above power-law assumption reflects a simple rule of mixtures applied only to the radial direction. The inhomogeneity parameter may be varied to obtain different distributions of the components materials through the radial direction of the cylinder.
According to Eq. (15), the stress-temperature moduli and humidity expansion coefficients of the present inhomogeneous hollow cylinder are given by:
where and are the corresponding stress-temperature moduli and humidity expansion coefficients of the homogeneous cylinder.
The temperature is generated at a position-dependent rate within the inner surface and it transfers to the outer one, while the outer surface is insulated. The internal energy generation within the inner and outer surface is described by the heat generating function:
where represents the constant rate of internal energy generation. However, the internal energy generation of the solid circular cylinder is described by the heat generating function:
To simplify the analytic solutions and calculations, the following dimensionless forms are used:
Now, the general solution of the heat conduction equation for the hollow circular cylinder, given in Eq. (3), is:
where and are arbitrary integration constants that determined from the boundary conditions given in Eq. (7) in the form:
So, the final form for the heat conduction of the hollow circular cylinder is given by:
Also the general solution of the moisture equation for the hollow cylinder, in Eq. (4) with the aid of the conditions in Eq. (8) is given by:
In addition, the solution of the charge equation of electrostatics is given by:
where is an unknown constant. Thus, the last part of Eq. (1) and the above equation with the aid of the inhomogeneous relation given in Eq. (15), gives:
Substituting the above equation into Eq. (1), the radial, hoop and axial stresses become:
Therefore, the equilibrium Eq. (5) with the aid of the above equation in the dimensionless form, yields:
where:
in which:
The general solution of Eq. (27) can be written as:
where and are arbitrary integration constants. These constants can be obtained from the mechanical boundary conditions given in Eq. (9). So, the complete general solution to the radial displacement as well as the temperature and moisture concentration may be used to obtain the electric potential. It is interesting here to get the function for the hollow cylinder. It reads:
Integrating Eq. (25) gives the electric potential in terms of additional arbitrary integration constant . Finally, the two constants and can be obtained by using the electric boundary conditions given in Eq. (10). Therefore, the final forms of stresses in the piezoelectric hollow circular cylinder can be fully obtained.
3.2. Closed-form solution for a solid circular cylinder
For the present solid cylinder ), the coefficients , , , , , and are changed through the radial direction according to the relations:
It is to be noted that the elastic coefficients, stress-temperature moduli and humidity expansion coefficients still constants for the solid cylinder, that is , and .
For the solid cylinder, the internal energy generation is described by the heat generating function:
So, one can solve Eq. (3) with the aid of the conditions given in Eq. (11) and the above heat generating function as:
Also the general solution of the moisture equation given in Eq. (4), in this case, is:
Here, the solution of the charge equation of electrostatics is the same as in the hollow cylinder. However, the last part of Eq. (1) gives:
and the corresponding radial, hoop and axial stresses will be:
The substitution of the above equation into Eq. (5) gives:
where:
in which:
Eq. (39) may be given for the present solid cylinder in details as:
Finally, the general solution of Eq. (38) is given by:
where and are arbitrary integration constants. Also, these constants can be obtained from the mechanical boundary conditions given in Eq. (13). The condition of tends to zero should be satisfied when . So, the complete general solution to the radial displacement as well as the temperature and moisture concentration may be used to obtain the stresses. Also, the electric potential may be obtained by integrating Eq. (36). In this case we will get an additional arbitrary integration constant . Finally, the two constants and can be obtained by using the electric boundary conditions given in Eq. (14).
4. Numerical examples and discussions
The proposed closed-form solution may be used for future comparisons with other investigators. Results for moisture, temperature, radial displacement, radial stress, hoop stress, axial stress, as well as the electrical potential are displayed graphically. The material constants are selected for the piezoelectric cylinder as follows [12]: 111 GPa, 220 GPa, 115 GPa, 15.1 V m N-1, –5.2 V m N-1, 0.0001 K-1, 0.00001 K-1, 0, 0.44 (wt% H2O)-1, 5.62×10-9 C2 (m2∙K)-1, 0.23 W (m K)-1, –2.5×10-5 C (m2 K)-1, –1.2×10-9 C (m2 K)-1, 1.2×102 Wm-1.
It is to be noted that the initial temperature and the final moisture are assumed to be 23 °C (room temperature) and 5 wt% H2O, respectively. The temperature and moisture concentration are independent of the pressures and the electric potentials. The numerical results for both cylinders are presented in dimensionless graphical forms. It should be noted that the following dimensionless forms are added:
4.1. Numerical results for a hollow circular cylinder
For the present hollow circular cylinder, the inner pressure used is 103 GPa and the outer one is given in terms of it, i.e., where is said to be the pressure load ratio. Similarly, the inner electric potential is 102 (W/A) while the external electric potential is where denotes the electric potential ratio. It is assumed that the inner-to-outer radii ratio is fixed as 0.2 m.
Fig. 1(a) demonstrates the plots of temperature across the thickness of the hollow cylinder. As the inhomogeneity parameter increases the temperature decreases. The maximum temperature occurs at the outer surface of the hollow cylinder . The temperature is constant at the inner surface of the hollow cylinder as set out originally in the boundary conditions for temperature. Fig. 1(b) (a plot of against ), shows that throughout the cylinder thickness, the moisture increases as the inhomogeneity parameter decreases. The moistures are constant at the inner and outer surfaces of the hollow cylinder, satisfying the constant boundary conditions for the moisture concentration. It is starting with and ending with . As can be seen in Fig. 1(b), the maximum change in occurs in the mid-range of cylinder .
Fig. 2 demonstrates the plots of the radial displacement throughout thickness of the hollow cylinder for different values of the inhomogeneity parameter , the pressure load ratio and the electric potential ratios . For , the value of has no effect on the radial displacement only when 32 (Fig. 2(a)). As increases, the radial displacement increases when and decreases when . However, for , Fig. 2(b) shows that the radial displacement increases as decreases when . The radial displacement increases as increases and gets its local maximum at the outer surface of the hollow cylinder. Fig. 2(c) shows the plots of versus for different values of the pressure load ratio . The displacement increases as increases only when . The variation of has no effect on when . The displacement increases as increases for . Fig. 2(d) shows the plots of versus for different values of the electric potential ratio . The displacement increases as increases only when . The variation of has no effect on when . The displacement increases as decreases for .
Fig. 1Distributions of T* and C* along the radial direction of the piezoelectric hollow cylinder for different values of n
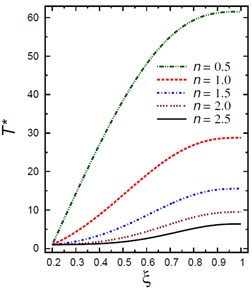
a) vs
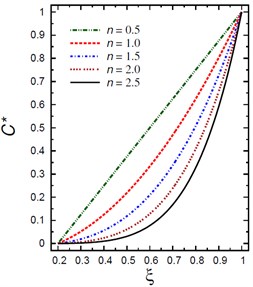
b) vs
Fig. 2Distribution of u- through the radial direction of the piezoelectric hollow cylinder for different parameters
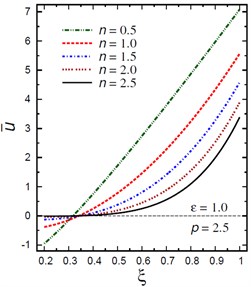
a) vs for different (1.0, 2.5)
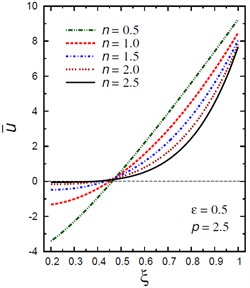
b) vs for different (0.5, 2.5)
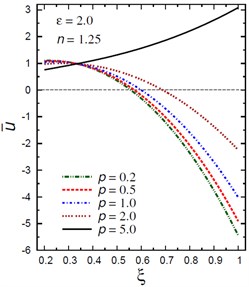
c) vs for different (2.0, 1.25)
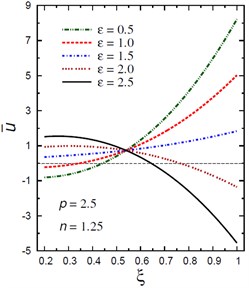
d) vs for different (2.5, 1.25)
Fig. 3Distribution of σ1 through the radial direction of the piezoelectric hollow cylinder for different parameters
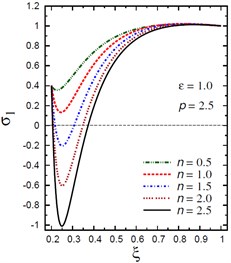
a) vs for different (1.0, 2.5)
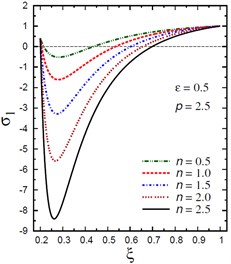
b) vs for different (0.5, 2.5)
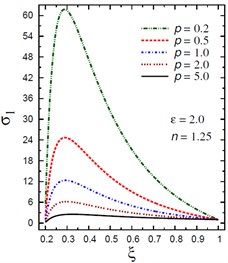
c) vs for different (2.0, 1.25)
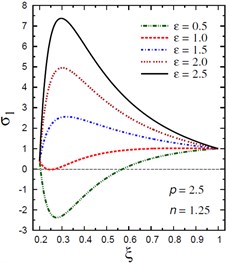
d) vs for different (2.5, 1.25)
Fig. 4Distribution of σ2 through the radial direction of the piezoelectric hollow cylinder for different parameters
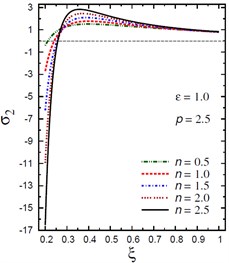
a) vs for different (1.0, 2.5)
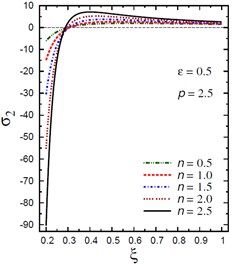
b) vs for different (0.5, 2.5)
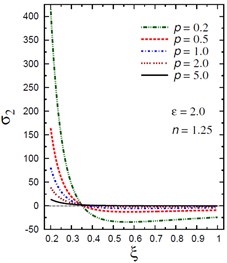
c) vs for different (2.0, 1.25)
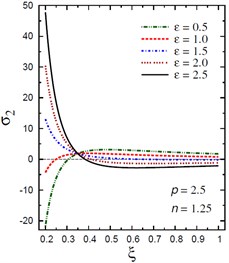
d) vs for different (2.5, 1.25)
The plots of the radial stress are showing in Fig. 3 through the radial direction of the hollow cylinder for different values of the inhomogeneity parameter , the pressure load ratio , and the electric potential ratio . As can be seen in Fig. 3(a), most radial stresses are compressive, i.e. they remain negative, in some interval through the radial direction of the cylinder for . However, all radial stresses are compressive in some interval through the radial direction of the cylinder for (Fig. 3(b)). The minimum radial stress occurs at while the maximum occurs at the outer surface of the cylinder. In addition, all radial stresses for are tensile, i.e. they remain positive as shown in Fig. 3(c). The maximum values of occur at the same interval of the cylinder. Fig. 3(d) shows that all stresses are tensile through the radial direction of the cylinder for . Once again, the minimum and maximum values of occur at the same interval of the cylinder. The radial stresses have fixed values at the boundaries of the hollow cylinder.
The plots of the hoop stress are showing in Fig. 4 through the radial direction of the hollow cylinder for different values of the inhomogeneity parameter , the pressure load ratio , and the electric potential ratio . As can be seen in Figs. 4(a), (b), the variation of has no effect on in some positions . The hoop stresses are no longer increasing and have their maximum values at . The absolute minimum value of occurs at the inner surface of the cylinder. Figs. 4(c), (d) show that the variations of and have no effects on at . The hoop stress decreases through the thickness of the cylinder for all values of the pressure load ratio (Fig. 4(c)) and for (Fig. 4(d)).
Fig. 5Distribution of σ3 through the radial direction of the piezoelectric hollow cylinder for different parameters
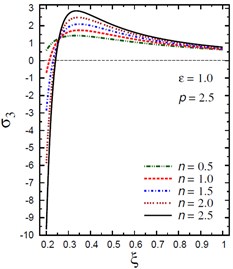
a) vs for different (1.0, 2.5)
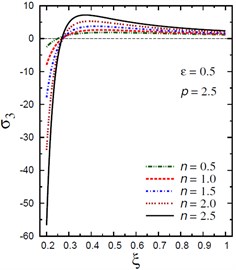
b) vs for different (0.5, 2.5)
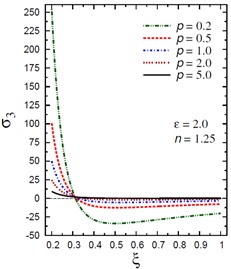
c) vs for different (2.0, 1.25)
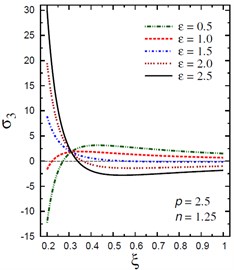
d) vs for different (2.5, 1.25)
The plots of the axial stress are showing in Fig. 5 through the radial direction of the hollow cylinder for different values of the inhomogeneity parameter , the pressure load ratio , and the electric potential ratio . Figs. 5(a), (b) show that the variation of has no effect on in some positions . The axial stresses are no longer increasing and have their maximum values at . The absolute minimum value of occurs at the inner surface of the cylinder. Figs. 5(c), (d) show that the variations of and have no effects on at . The axial stress decreases through the thickness of the cylinder for all values of the pressure load ratio (Fig. 5(c)) and for (Fig. 5(d)).
Fig. 6Distribution of Φ through the radial direction of the piezoelectric hollow cylinder for different parameters
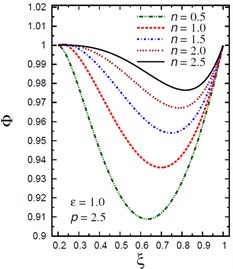
a) vs for different (1.0, 2.5)
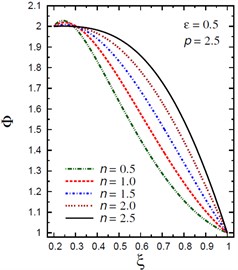
b) vs for different (0.5, 2.5)
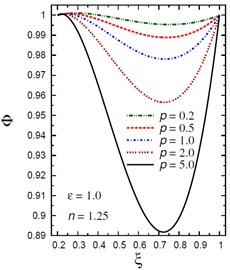
c) vs for different (2.0, 1.25)
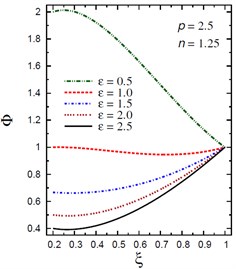
d) vs for different (2.5, 1.25)
Fig. 6 demonstrates the plots of the electric potential throughout the thickness of the hollow cylinder for different values of the inhomogeneity parameter , the pressure load ratio , and the electric potential ratio . As increases the electric potential increases for and for with . Fig. 6(a) shows that the electric potential is no longer decreasing and has its minimum values in some positions according to the value of . However, the absolute maximum values of occur at the inner and outer surfaces of the cylinder. Fig. 6(b) shows that the electric potential is no longer increasing and has its maximum values near the inner surface of the cylinder while the minimum value occurs at the outer surface of the cylinder. Fig. 6(c) shows that the electric potential decreases as increases. The absolute minimum values of occur at . Fig. 6(d) shows that the electric potential decreases as increases.
4.2. Numerical results for a solid circular cylinder
For the present solid circular cylinder, the outer pressure is 103 GPa where is said to be the pressure load ratio and the external electric potential is 102 (W/A) where denotes the electric potential ratio. Fig. 7(a) demonstrates the plots of temperature across the solid cylinder thickness. As the inhomogeneity parameter increases the temperature decreases. The maximum temperature occurs at . The temperature is constant at the outer surface of the cylinder as set out originally in the boundary conditions for temperature. Fig. 7(b) (a plot of against ), shows that throughout the cylinder thickness, the moisture increases as the inhomogeneity parameter decreases. The moisture is starting with at and ending with at .
Fig. 7Distributions of T* and C* along the radial direction of the piezoelectric solid cylinder for different values of n
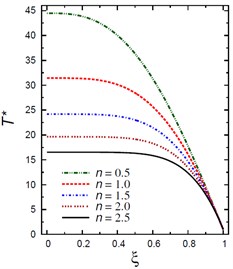
a) vs
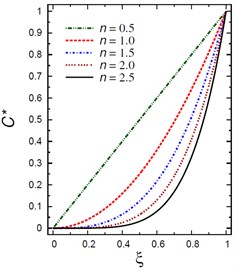
b) vs
Fig. 8Distribution of u- through the radial direction of the piezoelectric solid cylinder for different parameters
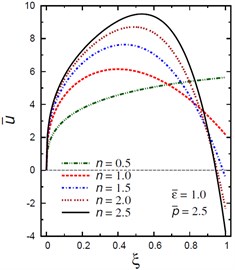
a) vs for different (1.0, 2.5)
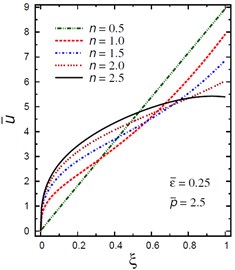
b) vs for different (0.5, 2.5)
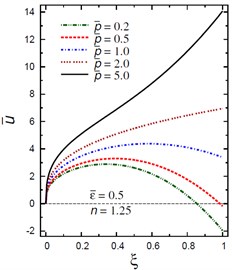
c) vs for different (2.0, 1.25)
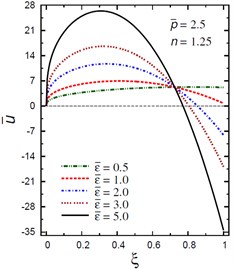
d) vs for different (2.5, 1.25)
Fig. 8 demonstrates the plots of the radial displacement throughout thickness of the solid cylinder for different values of the inhomogeneity parameter , the pressure load ratio and the electric potential ratios . Fig. 8(a) shows that increases as increases and its maximum occurs at the outer surface for . However, for is no longer increasing and has its maximum values at , 0.435, 0.485, and 0.53 for , 1.5, 2, and 2.5, respectively. Fig. 8(b) shows that the radial displacement increases as increases and the maximum values of occur at the outer surface of the cylinder. Fig. 8(c) shows that increases as increases and its maximum occurs at the outer surface for , only. However, for is no longer increasing and has its maximum values at , 0.39, and 0.58 for , 0.5 and 1, respectively. Fig. 8(d) shows that the variation of has no effect on at . Otherwise, has its maximum values: at for , at for 3, at for 2, at for 2, and at for .
Fig. 9Distribution of σ1 through the radial direction of the piezoelectric solid cylinder for different parameters
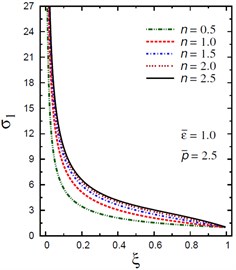
a) vs for different (1.0, 2.5)
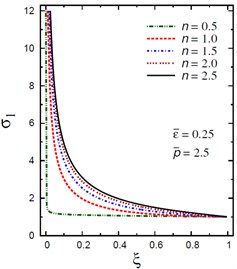
b) vs for different (0.5, 2.5)
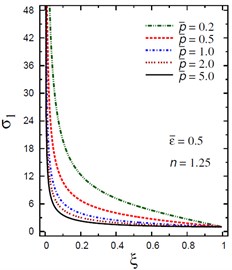
c) vs for different (2.0, 1.25)
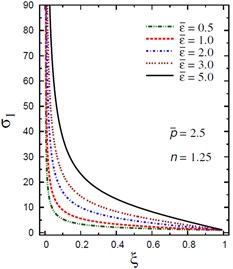
d) vs for different (2.5, 1.25)
The plots of the radial stress , hoop stress and axial stress are showing in Figs. 9-11 through the radial direction of the solid cylinder for different values of the inhomogeneity parameter , the pressure load ratio and the electric potential ratios . All radial stresses are compressive and the maximum values occur at the center of the cylinder while the minimum values are fixed at the outer surface of the cylinder. Most hoop stresses are compressive and the maximum values occur at the center of the cylinder while the minimum values are fixed at the outer surface of the cylinder. The variations of and have no effects on at . For , the hoop stress decreases through the thickness of the cylinder as decreases (Fig. 10(c)) and as increases (Fig. 10(d)). The maximum values of the axial stress occur at the center of the cylinder while the minimum values occur at the outer surface of the cylinder (Figs. 11(a), (d)). The variations of and have no effects on at . For , the axial stress decreases through the thickness of the cylinder as decreases (Fig. 11(c)) and as increases (Fig. 11(d)). The minimum axial stress occurs at for (Fig. 11(c)). Fig. 11(b) presents two minimum axial stresses: occurs at for and occurs at for .
Fig. 10Distribution of σ2 through the radial direction of the piezoelectric solid cylinder for different parameters
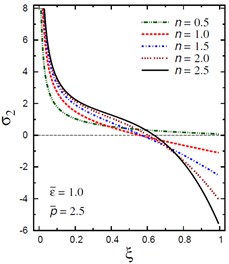
a) vs for different (1.0, 2.5)
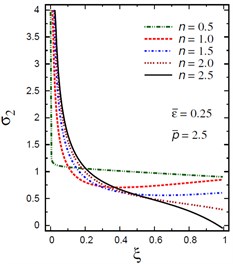
b) vs for different (0.5, 2.5)
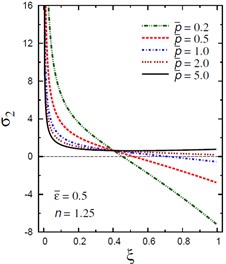
c) vs for different (2.0, 1.25)
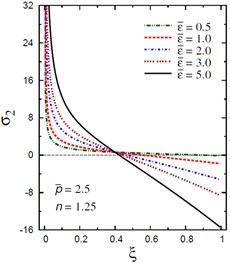
d) vs for different (2.5, 1.25)
Fig. 11Distribution of σ3 through the radial direction of the piezoelectric solid cylinder for different parameters
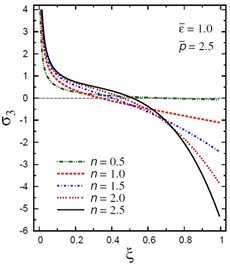
a) vs for different (1.0, 2.5)
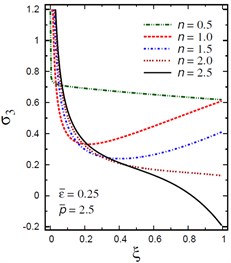
b) vs for different (0.5, 2.5)
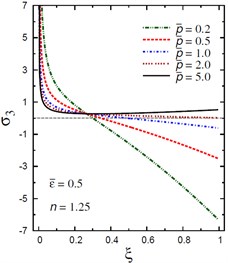
c) vs for different (2.0, 1.25)
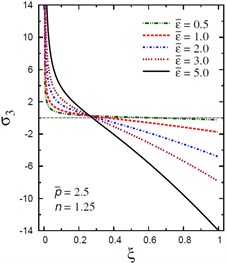
d) vs for different (2.5, 1.25)
Finally, Fig. 12 demonstrates the plots of the electric potential throughout the thickness of the hollow cylinder for different values of the inhomogeneity parameter , the pressure load ratio and the electric potential ratios . The electric potential is fixed at the center and outer surface of the solid cylinder. As increases the electric potential decreases for (Fig. 12(a)) and for (Fig. 12(b)). However, with the increase of and the electric potential increases (Fig. 12(c), (d)). For and , the electric potential has its absolute minimum value, –0.0725287 at as shown in Fig. 12(d).
Fig. 12Distribution of Φ through the radial direction of the piezoelectric solid cylinder for different parameters
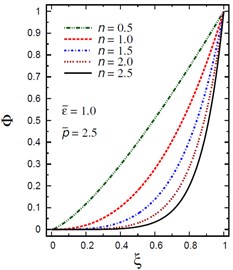
a) vs for different (1.0, 2.5)
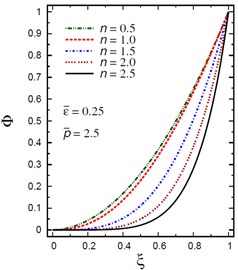
b) vs for different (0.5, 2.5)
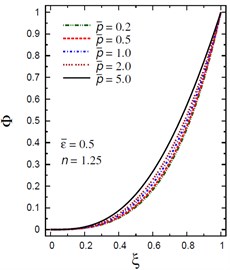
c) vs for different (2.0, 1.25)
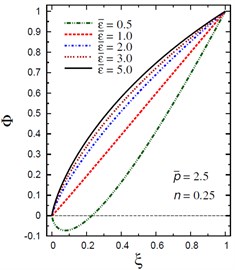
d) vs for different (2.5, 1.25)
5. Conclusions
The bending analysis of piezoelectric hollow and solid cylinder subjected to combined loading of external pressure and electric potential is developed to assess the effects of temperature and moisture concentration. The material properties are considered to be dependent on the radial direction of the cylinder. The exact closed-form solutions are given for inhomogeneous piezoelectric cylinders and applicable to different types of mechanical and electric boundary conditions. Numerical examples presented relate to the performance of inhomogeneous piezoelectric cylinders under different sets of environmental conditions. The results presented herein show that the inhomogeneity parameter, the pressure load ratio, the electric potential ratio, the initial temperature, and the final concentration have significant effects on the temperature, moisture, displacement, stresses, and electric potential.
References
-
Petroski H. J. On the finite torsion and radial heating of thermoelastic cylinders. International Journal of Solids and Structures, Vol. 11, Issue 6, 1975, p. 741-749.
-
Reddy J. N., Chin C. D. Thermomechanical analysis of functionally graded cylinders and plates. Journal of Thermal Stresses, Vol. 21, Issue 6, 1998, p. 593-626.
-
Ponnusamy P. Wave propagation in a generalized thermoelastic solid cylinder of arbitrary cross-section. International Journal of Solids and Structures, Vol. 44, Issue 16, 2007, p. 5336-5348.
-
Zenkour A. M. Thermoelastic analysis of an annular sandwich disk with metal/ceramic faces and functionally graded core. Journal of Thermoplastic Composite Materials, Vol. 22, Issue 2, 2009, p. 163-181.
-
Chitikireddy R., Datta S. K., Shah A. H., Bai H. Transient thermoelastic waves in an anisotropic hollow cylinder due to localized heating. International Journal of Solids and Structures, Vol. 48, Issue 21, 2011, p. 3063-3074.
-
Sharma J. N., Sharma P. K., Mishra K. C. Analysis of free vibrations in axisymmetric functionally graded thermoelastic cylinders. Acta Mechanica, Vol. 225, Issue 6, 2014, p. 1581-1594.
-
Kollár L. P., Patterson J. M., Springer G. S. Composite cylinders subjected to hygrothermal and mechanical loads. International Journal of Solids and Structures, Vol. 29, Issue 12, 1992, p. 1519-1534.
-
Kollár L. P. Three-dimensional analysis of composite cylinders under axially varying hygrothermal and mechanical loads. Computers and Structures, Vol. 50, Issue 4, 1994, p. 525-540.
-
Yang Yu-C., Chu S-S.,Lee H.-L., Lin S.-L. Hybrid numerical method applied to transient hygrothermal analysis in an annular cylinder. International Communications in Heat and Mass Transfer, Vol. 33, Issue 1, 2006, p. 102-111.
-
Wang B. L. Transient thermal fracture of a piezoelectric cylinder. Journal of Thermal Stresses, Vol. 28, Issue 2, 2005, p. 197-212.
-
Dai H.-L., Wang X., Dai Q. H. Thermoelectroelastic responses in orthotropic piezoelectric hollow cylinders subjected to thermal shock and electric excitation. Journal of Reinforced Plastics and Composites, Vol. 24, Issue 10, 2005, p. 1085-1103.
-
Dai H. L., Wang X. Magneto-thermo-electro-elastic transient response in a piezoelectric hollow cylinder subjected to complex loadings. International Journal of Solids and Structures, Vol. 43, Issues 18-19, 2006, p. 5628-5646.
-
Arani A. G., Barzoki A. A. M., Kolahchi R., Mozdianfard M. R., Loghman A. Semi-analytical solution of time-dependent electro-thermo-mechanical creep for radially polarized piezoelectric cylinder. Computers and Structures, Vol. 89, Issues 15-16, 2011, p. 1494-1502.
-
Dai H. L., Fu Y. M., Yang J. H. Electromagnetoelastic behaviors of functionally graded piezoelectric solid cylinder and sphere. Acta Mechanica Sinica, Vol. 23, Issue 1, 2007, p. 55-63.
-
Fesharaki J. J., Fesharaki V. J., Yazdipoor M., Razavian B. Two-dimensional solution for electro-mechanical behavior of functionally graded piezoelectric hollow cylinder. Applied Mathematical Modelling, Vol. 36, Issue 11, 2012, p. 5521-5533.
-
Zenkour A. M. Piezoelectric behavior of an inhomogeneous hollow cylinder with thermal gradient, International Journal of Thermophysics, Vol. 33, Issue 7, 2012, p. 1288-1301.
-
Arefi M. Nonlinear thermoelastic analysis of thick-walled functionally graded piezoelectric cylinder. Acta Mechanica, Vol. 224, Issue 11, 2013, p. 2771-2783.
-
Dai H.-L., Jiang H.-J. Analytical study for electromagnetothermoelastic behavior of a functionally graded piezoelectric solid cylinder. Mechanics of Advanced Materials and Structures, Vol. 20, Issue 10, 2013, p. 811-818.
-
Allam M. N. M., Zenkour A. M., Tantawy R. Analysis of functionally graded piezoelectric cylinders in a hygrothermal environment. The Advances in Applied Mathematics and Mechanics, Vol. 6, Issue 2, 2014, p. 233-246.
-
Zenkour A. M. Hygrothermoelastic responses of inhomogeneous piezoelectric and exponentially graded cylinders. International Journal of Pressure Vessels and Piping, Vol. 119, 2014, p. 8-18.
-
Zenkour A. M. Exact solution of thermal stress problem of an inhomogeneous hygrothermal piezoelectric hollow cylinder. Applied Mathematical Modelling, Vol. 38, Issue 24, 2014, p. 6133-6143.
About this article
The author is grateful for the supports for this work provided by The King Abdulaziz City for Science and Technology, Kingdom of Saudi Arabia and through King Abdulaziz University with Grand No. MS-34-61.
