Abstract
This paper deals with the investigation of the particular gearbox parameters’ effect on the noise of transmission. First, a single stage gearbox is designed and manufactured in order to validate input and results of the whole methodology. Second, the dynamic model is built for the single stage gearbox and each step is validated by an experiment. After well corresponding to the measurement, an additional simulation is performed to verify the influence. The impact of torque amount, imbalance position, backlash size, and torsion stiffness of each part is mainly investigated. The used method is able to determine the impact of each modification, thus it can be useful at the design phase and also during measurement or investigation of a real problem.
1. Introduction
Automotive industry is facing extensive demands on the on-road performance and mostly the acoustic comfort is gaining a key role for marketing issues. Global decrease of the engine’s overall emitted noise leads to higher perception of the other components’ influence. This noise was previously masked but nowadays can be crucial for customer’s decision. Therefore, it is necessary to investigate each component contribution and focus on the design which can influence noise, vibration and harshness (NVH) characteristics. One of these important components is a transmission unit.
From the noise reduction’s point of view it is beneficial to carry out the design optimization which cannot be utilized without an appropriate knowledge of the vibration cause principle and following spreading into the surroundings together with the noise creation.
1.1. Literature review
The noise emitted by the transmission housing stands for more than 90 % of the whole transmission system noise and the common basic approach, which is widely used for optimization, is the modal analysis [1, 2]. The main excitation of the transmission housing originates in the gear meshing impact. The helical tooth gear pair is dominantly used in the automotive industry, therefore it still belongs to one of the contemporary research topics in this area [3]. The helical tooth is more complicated than spur gear, because of oblique line of contact in case of the helical gears, but the large vibration amplitudes with strongly nonlinear behavior is presented at the spur gears, which is undesirable [4]. Some simplified models exist – which use sinusoidal stiffness variation to represent a helical gear contact and rectangular stiffness in case of spur gear. According to [5] the finite element method is commonly used for contact stiffness determination. A distinct approach to get high level complex model is developed as well in [6]. Subsequently, these inputs can be used for calculating vibrations and noise emitted by the transmission housing, or to investigate the special effects, e.g. rattle noise [7, 8].
The presented paper deals with the first variant, where the vibrations of the housing are studied. To create the multibody dynamics model, some additional inputs are necessary. Bearings or shafts stiffness can significantly influence model behavior and also the noise results [9].
Based on the dynamics simulations the additional effect of transmission parameters can be investigated [10-12]. The simulation methodology should be validated to verify the correct inputs and outputs, this approach is used in wide spectrum of studies [4, 8, 13].
2. The experimental gearbox concept
For the gearbox dynamics solution the concept of the single-stage gearbox unit is chosen, see Fig. 1. It is due to a relative simplicity of a shape but still complex behavior, as in the case of the common transmission. First step of such study should always be to provide reliable experimental validations. Comparison with real measurements is necessary for the computational dynamics characteristic evaluation in case of putting together the methodology. Once the procedure on this simplified gearbox unit is complete, it can be extended and applied to any transmission.
The gearbox mechanism includes helical gears with 31 and 27 teeth, input and output shaft, which have identical dimensions and tapered roller bearings. The gearbox is constructed as a simple body with two pairs of bearing housings, which can be randomly substituted. It enables universal usage of the gearbox for the testing purposes. The parameters of the whole gearbox were aimed to correspond with the heavy duty truck gearbox. Material used for input and output shaft is steel class S235JR. Both gears are made of 20CrMo4, and the gearbox housing of S235JR.
Fig. 1Single stage gearbox

2.1. Multi body simulation model
The choice of the multi body simulation (MBS) approach is beneficial since it can initially incorporate most of the transient regimes, because of the time domain solution. The summarized vibrational behavior consists of superposition of each function part motion as the result of the gear meshing excitation. To set up this model depends on the precise input data, as well as on their experimental validation.
The fundamental part of the MBS model is gear mesh contact connected to the flexible shafts which are assembled in the gearbox housing. Stiffness and damping characteristics of the situated joints (bearings, gear mesh) are also included. The complex evaluation process of the described model is very wide and mostly consists of the experimental and computational modal analysis for the flexible parts behavior correlation. Also computational and experimental harmonic analysis is performed for further damping specification and critical locations identification.
Numerical simulations of the experimental gearbox are attained from the parametrical studies of the several input parameters’ influence prediction. Results of this work are described in the following chapters.
3. Results of the gear parameters geometry change
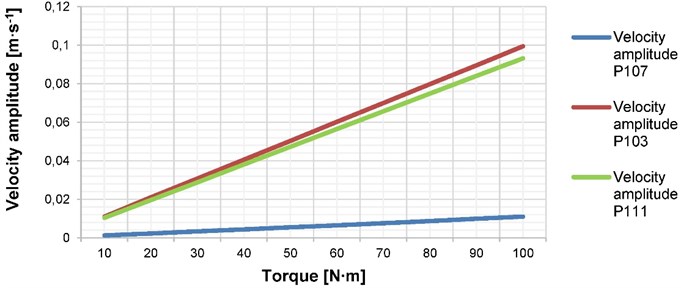
The effect of each parameter is investigated at the constant value of the remaining ones. First, the effect of the output torque is investigated. The torque is changed from 0 Nm up to 100 Nm. The dependence is linear, see Fig. 2. The surface normal velocity is observed at three locations.
Fig. 2The dependence of the normal surface velocity on the constant output torque
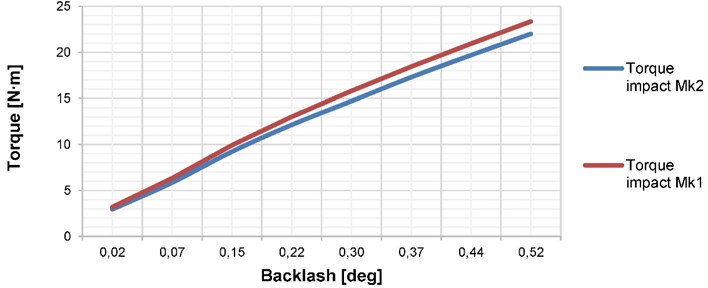
As the next parameter the backlash is investigated. The change of the backlash did not have significant impact on the surface normal velocity, thus the torque is compared, see Fig. 3. The output torque is set to zero value to emphasize the effect. Even slight change in the backlash leads to significant torque impact. This influence becomes stronger in case of the variable rotational speed input.
Fig. 3The dependence of the torque on the backlash value
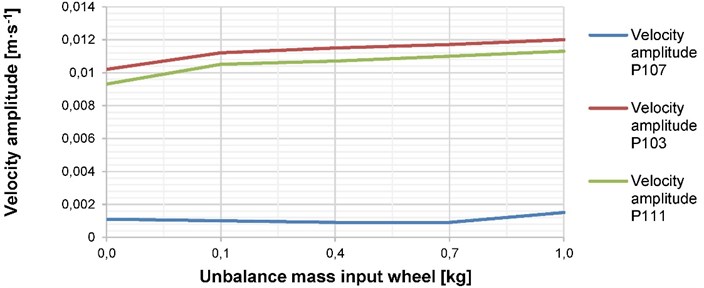
The unbalance is modeled by the mass point, which is placed at the radial direction on the driver wheel. Afterwards, the second mass point is moved to driven wheel location. The influence on the normal surface velocity is shown in the Figs. 4, 5.
Fig. 4The dependence of the normal surface velocity on the unbalance mass located on the input wheel
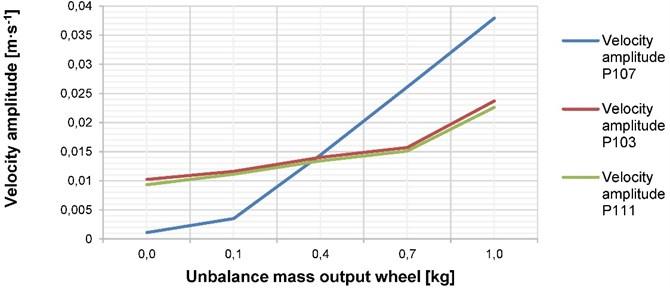
It is evident that the unbalance mass on the output gear produces approximately two times higher amplitudes of the surface normal velocity. The cause is in the unsymmetrical gearbox geometry arrangement which prefers response paths close to the output shaft.
Fig. 5The dependence of the normal surface velocity on the unbalance mass located on the output wheel
Nevertheless, the transmission is exposed to the patchy load from the propellant machine, thus the angular speed is simulated as sinusoidal. The overall results in form of 3D waterfall diagrams are shown in Figs. 6, 7.
Plotted graphs are for the same point and similar working conditions. It means same applied torque as well as the variable rotational speed. The only difference is in adding relatively high unbalance mass on the both gears.
Fig. 6Waterfall diagram with the unbalanced gear for the point 103
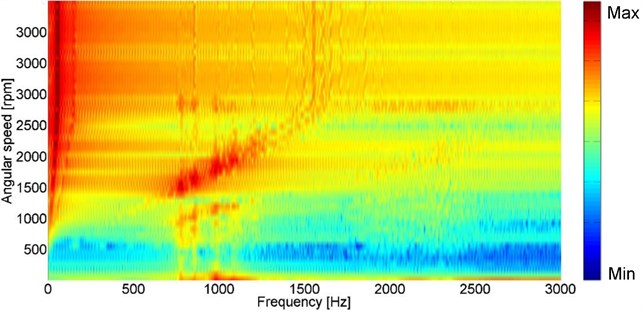
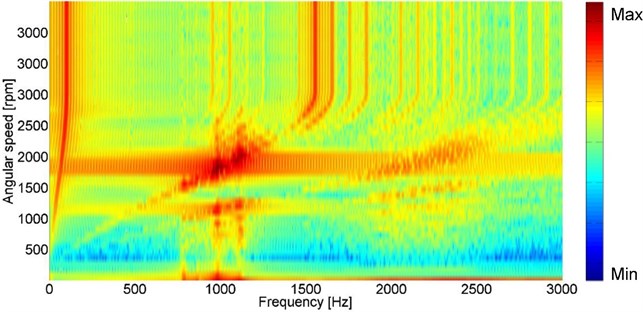
Fig. 7Waterfall diagram without the unbalanced gear for the point 103
4. Conclusions
The presented paper deals with investigation of the effect of parameters on the gearbox vibration which has direct impact on the emitted noise. MBS model of the experimental single stage gearbox used in this parametrical study is firstly developed and validated by wide spectrum of measurement, but this process is not a part of the paper presented. The main focus is on the investigation of the torque, backlash and unbalance effect.
The influence of the rising braking torque applied on the output shaft has strictly linear function, on the other hand, the increasing gear mesh clearance leads to a quadratic dependence of the beginning torque stroke. In this case the output torque condition is set to zero, and therefore, the initial load originates in the collision when the gears touch each other.
The difference between balanced and unbalanced model is presented in the last part and shows two interesting phenomena. The second gear mesh order amplitudes are higher in frequency range from 2000 to 2500 Hz in the variant without unbalance. Also maximum resonance amplitudes located in the first gear mesh order are higher. Obviously presence of the unbalance in the model significantly changes the gearbox dynamic behavior in a way that signs of the meshing frequency are attenuated. On the other hand its presence stimulates wide frequency excitation.
Explanation from the energy balance point of view seems logical. In the both variants there is the same amount of the input energy provided. Without unbalance most of the energy is brought into the gear mesh contact from which the excitation is radiated further more. Dominantly when reaching the resonances allocated in isolated singular frequencies, characteristic for the gearbox housing. When the unbalance is included, some part from the energy sum is consumed for this part motion. Also frequency of the unbalance motion corresponding with the rotational speed is relatively low, therefore its higher orders excitation can be in the waterfall diagram noticed much more in the chosen range up to 3 kHz.
References
-
Yongxiang L., Lihong J., Wenquan S., Liwen N., Youjia Z. An efficient optimal design methodology for abnormal noise control of automobile transmission in the neutral idle condition. Journal of Vibroengineering, Vol. 16, Issue 1, 2014, p. 351-359.
-
Ashwani K., Himanshu J., Faraz A., Pravin P. P. Dynamic vibration characteristics analysis of truck transmission gearbox casing with fixed constraint of vehicle frame based on FEA. Procedia Engineering, Vol. 97, 2014, p. 1107-1115.
-
Andersson A., Vedmar L. A dynamic model to determine vibrations in involute helical gears. Journal of Sound and Vibration, Vol. 260, 2003, p. 195-212.
-
Kang M. R., Kahraman A. An experimental and theoretical study of the dynamic behavior of doublehelical gear sets. Journal of Sound and Vibration, Vol. 350, 2015, p. 11-29.
-
Lin T., Ou H., Li R. A finite element method for 3D static and dynamic contact/impact analysis of gear drives. Computer Methods in Applied Mechanics and Engineering, Vol. 196, 2007, p. 1716-1728.
-
Liu L. A multibody system model for meshing gears. Applied Mechanics and Materials, Vol. 4447, 2011, p. 1273-1278.
-
Bozca M., Fietkau P. Empirical model based optimization of gearbox geometric design parameters to reduce rattle noise in an automotive transmission. Mechanism and Machine Theory, Vol. 45, 2010, p. 1599-1612.
-
Huijun Y., Yanfang L., Xiangyang X., Junbin L. Study on vibration characteristics and tooth profile modification of a plus planetary gear set. Journal of Vibroengineering, Vol. 16, Issue 2, 2014, p. 954-964.
-
Sawalhi N., Randall R. B. Simulation of the vibrations produced by extended bearing faults in gearboxes. Proceedings of First Australasian Acoustical Societies’ Conference, Christchurch, New Zealand, 2006, p. 541-548.
-
Wijianto Vibration analysis of dynamic modelling of gear pair in mesh due to torque and load on the system. Journal Teknik Gealgar, Vol. 18, 2007, p. 141-148.
-
Mazeika P., Didziokas R., Barzdaitis V., Bogdevicius M. Dynamics and reliability of gear driver with antifriction bearings. Journal of Vibroengineering Vol. 10, Issue 2, 2008, p. 217-221.
-
Fernandey A., Iglesias M., de-Juan A., Garcia P., Sancibrian R., Viadero F. Gear transmission dynamic: effect of tooth profile deviations and support flexibility. Applied Acoustics, Vol. 77, 2014, p. 138-149.
-
Guo Z., Eritenel T., Ericson T. M., Parker R. G. Vibro-acoustic propagation of gear dynamics in a gear-bearing-housing system. Journal of Sound and Vibration, Vol. 333, 2014, p. 5762-5785.
About this article
The research leading to these results has received funding from the Ministry of Education, Youth and Sports under the National Sustainability Programme I (Project LO1202) and University Specific Research project Research of Progressive Methods for Drivetrain Dynamics, Reg. No. FSI-S-14-2334. This support is gratefully acknowledged.
