Thermodynamic performance analysis and improvement for cross-saddle type slide of electric discharge machine

Li, Fuping; Li, Ying; Liu, Zhifeng; Hu, Qiushi; Liu, Jianyong; Li, Yan

Vibroengineering Procedia

Browse Procedia

Published: 18 September 2015

Check for updates

Thermodynamic performance analysis and improvement for cross-saddle type slide of electric discharge machine

Fuping Li¹

Ying Li²

Zhifeng Liu³

Qiushi Hu⁴

Jianyong Liu⁵

Yan Li⁶

^{1, 2, 3, 4}College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, Beijing, China

^{5, 6}Beijing Institute of Electro-Machining, Beijin, China

Corresponding Author:

Ying Li

Cite the article Download PDF

Downloads 1304

Abstract

As the key connecting part of the electrical discharge machine (EDM), the slide of cross-saddle type directly impacts the machine tool’s machining accuracy. In this paper, the friction heats of the bearing and ball screw pair are the main heat source, considering the thermal contact resistance (TCR), making the coupled thermos-mechanical deformation analysis for the slide applied the finite element analysis (FEA) software. According to the analysis result, the temperature field and thermal deformation considering the TCR are closer to the actual working condition; in addition, proposed two kinds of optimization design structures. Using the same conditions to analyze these structures, finding that a drop in temperature and the thermal deformation, especially the cellular form of stiffened plate structure. The analysis results not only provide a basis that the further optimization of the slide structure, but also highlight the advantages of the honeycomb structure.

1. Introduction

With the rapid development of aerospace enterprise, higher and higher demands were provided for the material and precision of the key components, the traditional processing equipment is difficult to meet these requirements. In order to solve this problem, machinery industry at home and abroad developed a variety of special processing equipments. The EDM was widely used, because it has these feature: to overcome the strong by applying soft methods, precision with subtle, shape lifelike, and high degree of automation [1]. Machine tool influenced of internal and external heat source in the working process, and result in uneven temperature distribution, the machine parts occurred different extent of thermal deformation, which destroy the relative motion between the machine tool parts, reduce the machining accuracy of machine tools. According to statistics found that: In the precision machining, machine tool thermal deformation caused error occupied the total error’s 40 %-70 % [2].

In this paper, the friction heat of the bearing and ball screw pair are the main heat source, in the process of heat transfer, due to the contact surface is not completely, so the thermal contact resistance (TCR) was introduced. In addition, the screw rotation will drive the surrounding gas movement, resulting in a forced convection phenomena, based on the above analysis, established the initial and boundary conditions of the slide thermal modal. Using Solidworks and ANSYS Workbench software established finite element model (FEM) of slide, on this basis, the coupled thermo-mechanical deformation analysis was carried out, according to the result of analysis, put forward two kinds of structure improvement plan.

2. The coupled thermo-mechanical deformation analysis of the slide

In order to get the any position temperature field and thermal deformation of the slide, under the condition of the temperature unknown, adopt the coupled thermo-mechanical deformation simulation analysis of the indirect method for the slide, the analysis flow chart is shown in Fig. 1.

In order to ensure the strength and stiffness of the slide meet the requirements, selected the gray cast iron and bearing steel material, main parameters are shown in Table 1.

Fig. 1The thermal coupling deformation analysis flow chart of the slide

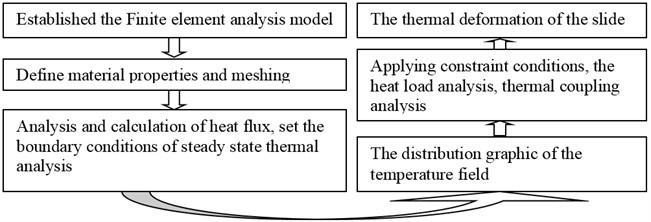
Table 1The material parameters of the slide

Part	Material	Density Kg/m³	Modulus of elasticity GPa	Poisson‘s ratio	Specific heat capacity J/(Kg·°C)	Expansion thermal coefficient °C^-1	Thermal conductivity W/(m·°C)
Slide	Gray cast iron	7200	110	0.28	447	1.1×10^-5	52
Bearing and nut	Bearing steel	7810	207	0.3	460	1.2×10^-5	45

2.1. The establishment of the finite element model

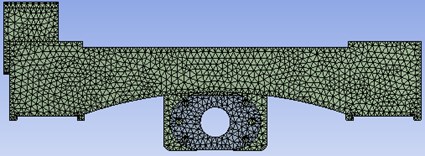
The stand or fall of the FEM directly related to the accuracy of the analysis and the computational cost. There are two kinds of methods to establish the slide’s FEM: the firstly, adopted the 3D-CAD software to establish the entity model of the slide, and then through the initial graphics exchange specification (IGES) imported into the FEA software; the second is the modeling function of ANSYS Workbench software itself, on the basis of ignoring details, obtaining a geometric approximate solution of the model. Because the latter's modeling function is weak, adopted the Solidworks software build the 3D entity model of the slide, and then imported to ANSYS Workbench software, adopted the combining method of the automatic and manual mesh grid to mesh for the entity model, the FEM is shown in Fig. 2.

Fig. 2The finite element model of the slide

2.2. Analysis and calculation of the heat source

The main heat source that impacted the thermal characteristics of machine tool are heat cutting, electrical heat, friction heat transmission and radiation [3]. Because the heat shield is equipped between the slide and motor, at the same time, EDM electrodes’ discharge process in the working liquid, there is less heat conducts to the slide, the temperature rise is small, less radiant heat, therefore, above the heat source can be negligible. For EDM work in motor and ball screw is a continuous movement, so the slide’s heat source mainly comes from the friction of the bearing and ball screw pair.

2.2.1. Bearing friction heat

The bearing, as the main supporting parts, will produce a lot of friction heat when the motor drives the ball screw rotation, the heat is mainly caused by the friction between the rolling body and the bearing of inner and outer ring, its size is directly related to the friction torque. Calculating formula is [4]:

1

Q_{b} = 1.047 \times 10^{- 4} n M,

2

M = M_{0} + M_{1},

where $n$ is bearing rotating speed; $M$ is bearing friction torque, mainly including load friction torque $M_{1}$ and the lubricant viscosity friction torque $M_{0}$ .

Because of rolling bearing friction torque is nonlinear relationship, the friction torque will be different with the change of time for the same type or even the same set of bearing. Due to the low speed of the EDM, therefore, the current apply the approximation algorithm of bearing friction torque is put forward by Palmgren. Calculation formula is:

3

v n > 2000 c S t, M_{0} = 10^{- 7} f_{0} {(ν n)}^{2 / 3} d_{m},

4

v n < 2000 c S t, M_{0} = 160 \times 10^{- 7} f_{0} d_{m}^{3},

5

M_{1} = f_{1} P_{1} d_{m},

where $f_{0}$ is a empirical constant related to the bearing type; $d_{m}$ is bearing pitch diameter; $ν$ is kinematic viscosity of lubricant about the working temperatures; $f_{1}$ is a coefficient related to the bearing types and load; $P_{1}$ is a calculation load to determine the bearing friction torque.

2.2.2. The friction heat of the ball screw pair

The friction heat of the ball screw pair is mainly caused by the complexity of raceway surface structure, the heat cannot spread out in time, has a certain lag, make uneven temperature distribution of the raceway surface. Its size is associated with the friction torque of ball screw pair, expression is[5, 6]:

6

Q = 0.12 π n M,

where $n$ is speed of the screw; $M$ is friction moment of the ball screw pair, mainly including sliding friction torque $M_{h}$ and rolling friction moment $M_{g}$ between the ball and raceway work, friction torque between the ball $M_{b}$ , friction torque betweem ball bearing and reverser $M_{f}$ , and viscous friction torque of lubricant $M_{ν}$ . Computation formula is:

7

M = M_{h} + M_{g} + M_{b} + M_{f} + M_{ν},

where $M_{h}$ , $M_{g}$ , $M_{b}$ , $M_{f}$ , $M_{ν}$ can be detected from the literature [6].

2.3. The initial and boundary conditions

The above calculated friction heat in the form of heat generation rate applied to the FEM of slide. Heat generation rate is the flow of heat of the per unit volume, use the formula is expressed is:

8

q = Q / V,

where $V$ is the volume of the bearing or screw nut.

In the study of the past, many people assume: two solid contact surface is completely contact, namely the TCR is 0. In fact, the contact area occurs a small number of micro convex peak, is a very small proportion account for the nominal contact area.

2.3.1. The calculation of the TCR

Convenient to measure and calculation, by using the Monte Carlo Model for numerical calculation of TCR, its expression is:

9

\{\begin{array}{l} 1 / R_{c} = \sum_{i = 1}^{N_{c}} 1 / R_{c i}, \\ R_{c i} = f (a / b) / 2 a K_{s}, \\ f (a / b) = 1 - 1.40918 (a / b) + 0.3381 {(a / b)}^{3} + 0.06792 {(a / b)}^{5}, \\ 1 / K_{s} = 1 / K_{1} + 1 / K_{2}, \end{array}

where $R_{c}$ is TCR; $K_{1}$ , $K_{2}$ are thermal conductivity of the contact materials respectively; $a$ , $b$ are contact zone radius of disk and hot flow channel radius respectively.

2.3.2. The calculation of convection heat transfer coefficient

There are three kinds of way of heat transfer: conduction, convection and radiation. Due to the temperature rise of the sliding seat is small when the machine tool is working, so mainly take into consideration the conduction and convection for the analysis of slide, thermal conductivity is given in Table 1, the size of the convective heat transfer can accord the Newton cooling formula obtained:

10

Q = h A (t_{f} - t_{w}),

11

h = N_{u} λ / L,

where $h$ is convective heat transfer coefficient; $N_{u}$ is Nusselt number; $λ$ is thermal conductivity; $L$ is feature sizes.

The convective heat transfer between slide and surrounding gas includes natural convection heat transfer, and the forced convective heat transfer is caused by lead screw drive the surrounding gas movement. The calculating formula of the Nusselt number [7, 8] respectively:

Natural convection:

12

N_{u} = C {(G_{r} \times P_{r})}^{n},

13

G_{r} = g β ∆ t L^{3} / ν^{2},

where $C$ , $n$ are constant; $G_{r}$ is Grashof numeral; $P_{r}$ is Prandtl number; $g$ is acceleration of gravity; $β$ is expansion coefficient; $ν$ is kinematic viscosity.

Forced convection:

14

N_{u} = 0.133 R_{e}^{2 / 3} P_{r}^{1 / 3}, (R_{e} < 4.3 \times 10^{5}, 0.7 < P_{r} < 670),

where $R_{e}$ is Renault coefficient of air.

Assuming that the air flow is laminar, the up and down surface of the slide are large flat, Planck number, expansion coefficient is constant, the speed of the ball screw pair for 600 r/min, $g =$ 9.81 N/K_g, other parameters can be detected from the literature [9], using the Eqs. (10)-(14) can obtain that forced convection heat transfer is the natural convection heat transfer of about seven times.

2.4. Results analysis

Through the above calculation, the heat flux and boundary conditions have been divided in the FEM, there are two kinds of circumstances that applying and without TCR, the Fig. 3 and 5’s temperature field cloud picture are obtained by steady state thermal analysis; and then the temperature field distribution as the load, applying power load and fixed constraint to the statics analysis, its total deformation nephogram as shown in Fig. 4 and Fig. 6.

We can see from the diagram that the highest temperature appears in bearing and nut, the highest temperature is 42.036 °C when without the TCR, the highest temperature of 42.541 °C when with the TCR, the proportion of the highest temperature on the slide is decreases, and showed the TCR impact the heat transfer. Through the analysis of the thermal deformation find the maximum thermal deformation occurred in the connected to the bearing parts, the greatest thermal deformation is 57.216 μm without the TCR, applying the TCR is 57.774 μm.

Fig. 3The temperature field without TCR

Fig. 4The thermal deformation without TCR

Fig. 5The temperature field with TCR

Fig. 6The thermal deformation with TCR

Fig. 7Structure 1

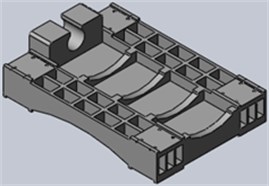
Fig. 8Structure 2

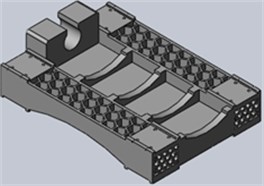
Table 2The biggest change of the highest temperature and thermal deformation of the two kinds of structure

	The highest temperature drop °C	The biggest thermal deformation μm	The thermal deformation of relative value
Structure 1	0.41	0.693	4.29 %
Structure 2	2.25	6.635	41.08 %

3. Measures of reducing thermal deformation

Reduce machine tool thermal deformation can consider from such aspects: decrease the TCR or increase the TCR, and optimize the structure of the slide. Among them, reduce the TCR can make heat concentrated in bearing and nuts, make the deformation of ball screw pair serious; increasing the TCR, the decrease of the thermal deformation volume is small, so consider slide the optimization of the structure.

According to the original structure set different forms of stiffened plates. Through the Solidworks software to establish 3D model of the structure of the two, as shown in Figs. 7 and 8.

Using the same heat source and boundary conditions to make the coupled thermo-mechanical deformation analysis on the two structures, the highest temperature and thermal deformation’s position constant, the change amount shown in Table 2.

4. Conclusions

The cross saddle type slide is the key parts of the EDM, its thermal deformation has much effect on the machining accuracy. This article is based on Solidworks and ANSYS Workbench software established finite element model of the slide by applying the initial and boundary conditions, the deformation of thermal coupling analysis was carried out on the slide, found that the TCR had a great influence on the distribution of temperature field, and according to the analysis results on the basis of the original structure set up different forms of stiffened plate, two kinds of structure optimization design are obtained. Compared with the original structure, two kinds of schemes of intensity and rigidity were increased. In addition, in terms of the thermal deformation, structure a temperature drop of 0.41 °C, thermal deformation decreased by 4.29 %; structure of temperature drop of 2.25 °C, thermal deformation decreased by 41.08 %. Results show that through the reasonable arrangement of stiffened plates slide in the form and position, can reduce the thermal deformation, slide not only highlight the advantages of the honeycomb structure, and to provide the basis for the further optimization of slide structure.

References

Cao Fengguo Special Processing Manual. China Machine Press, Beijing, 2010.

Search CrossRef
Ramesh R. E1t or Compensation in machine tools-a review part l: thermal errors. International Journal of Machine Tools and Manufacture, Vol. 40, 2000, p. 1257-1284.

Search CrossRef
Cheng Bo, Yin Guofu, Liu Lixin, et al. Thermal analysis and improvement for cross slide of gantry machining center. Machinery Design and Manufacture, Issue 11, 2011, p. 210-212.

Search CrossRef
Wang Yun, Wu Meiping, Zuo Xiaofang Thermodynamic performance analysis and experiment research on TK69 floor-type milling boring ram. Modular Machine Tool and Automatic Manufacturing Technique, Issue 1, 2015, p. 34-41.

Search CrossRef
Tianri Heren Solution for Heating of Ball Screw and Environmental Engineering. World Manufacturing Engineering and Market, Vol. 6, Issue 3, 2004, p. 65-67.

Search CrossRef
Han Xinjian High-speed Ball Screw Performance Analysis and Experiment Study of Friction. Lanzhou University of Technology, Lanzhou, 2011.

Search CrossRef
Guo Xuexiang, Hu Youmin, Xia Junyong, et al. Study on thermal deformation of machine tools’ slide guide based on FEA. Modular Machine Tool and Automatic Manufacturing Technique, Issue 3, 2007, p. 8-11.

Search CrossRef
Guan Lingbo Thermodynamic Analysis of High-speed Overloaded Ball Screw. Zhejing University, Zhejing, 2014.

Search CrossRef
Yang Shiming, Tao Wenquan Heat Transfer (Fourth Edition). Higher Education Press, Beijing, 2006.

Search CrossRef

About this article

Received

Accepted

17 July 2015

Published

18 September 2015

SUBJECTS

Mechanical vibrations and applications

Keywords

EDM

slide

TCR

thermo-mechanical deformation analysis

FEA

Acknowledgements

National Science and Technology Major Project of the Ministry of Science and Technology of China (2013ZX04011-013) and Jing-Hua Talents Project of Beijing University of Technology.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.