Abstract
Based on the Rayleigh beam theory, the forced transverse vibrations of an elastically connected simply supported double-beam system with a Pasternak middle layer subjected to compressive axial load are investigated. It is assumed that the two beams of the system are continuously joined by a Pasternak layer. The dynamic responses of the system caused by arbitrarily distributed continuous loads are obtained. The effect of Pasternak layer on the forced vibrations of the Rayleigh double-beam system are discussed for one particular case of excitation loading. The properties of the forced transverse vibrations of the system are found to be significantly dependent on the compressive axial load and shear foundation modulus of Pasternak layer. Vibrations caused by the harmonic exciting forces are discussed, and conditions of resonance and dynamic vibration absorption are formulated. The important result on which this paper puts emphasis is that the magnitudes of the steady-state vibration amplitudes become smaller when the shear Pasternak modulus increases and Pasternak layer can reduce the magnitudes of the steady-state vibration amplitudes more than a Winkler elastic layer. Thus the Rayleigh beam-type dynamic absorber with a Pasternak layer can be used to suppress the excessive vibrations of corresponding beam systems instead of those with a Winkler elastic layer
1. Introduction
A great number of mechanical systems are complex structures composed of two or more basic mechanical systems whose dynamic behaviors are conditioned by their interactions. The systems connected by an elastic layer constitute one group of such mechanical structures which are commonly encountered in mechanical systems, construction and aeronautical industry. Such mechanical systems are exposed to an increased possibility of creating resonance conditions which can cause breakage and damage. These models are important as they give the initial approximation of the solution and a general insight into a dynamic behavior of the system at slight motion. The problem concerning the vibrations of beams joined by a Winkler elastic layer has attracted the interest of a large group of scientists. The problem of two elastically connected beams jointed by the Winkler elastic layer has been investigated in order to determine the conditions for the behavior of the system acting as a dynamic absorber in technical practice.
A mathematical model was developed by Seelig and Hoppman [1]. They investigated the problem of an impulse load effect on a beam and generated a system of partial differential equations describing its vibration. The obtained theoretical and experimental results which confirmed a sound approximation of an analytical solution obtained for slender beams at small transverse motions using the Euler-Bernoulli theory.
Oniszczuk [2, 3] analyzed the problem of free and forced vibration of two elastically connected Euler-Bernoulli beams. He determined analytical solutions for amplitudes functions and vibration modes. He discussed the effect of the stiffness of the elastic inter-layer on the frequencies and amplitudes of the system. He determined the conditions for the occurrence of resonance and the behavior of the system as a dynamic absorber.
The analysis of the system composed of two connected beams was carried on by Zhang et al. [4, 5]. They presented analytical solutions for natural frequencies of the system as a function of axial compression force impact and their effect on the vibration amplitude. They determined the co-dependency between the system’s critical force and the Euler critical load as a function of an axial force of the other beam.
The behavior of foundation materials in engineering practice cannot be represented by foundation model which consists of independent linear elastic springs. In order to find a physically close and mathematically simple foundation model, Pasternak proposed a so-called two-parameter foundation model with shear interactions. In an attempt to find a physically close and mathematically simple representation of an elastic foundation for these materials, Pasternak [6] proposed a foundation model consisting of a Winkler foundation with shear interactions. This may be accomplished by connecting the ends of the vertical springs to a beam consisting of incompressible vertical elements, which deforms only by transverse shear.
In Wang and Stephens [7] and De Rosa [8], the natural vibration of a Timoshenko beam on a Pasternak-type foundation is studied. Frequency equations are derived for beams with different end restraints. A specific example is given to show the effects of rotary inertia, shear deformation, and foundation constants on the natural frequencies of the beam.
Stojanovic et al. [9] analyzed free vibration and static stability of two elastically connected beams with the Winkler elastic layer in-between considering the effects of rotary inertia and transverse shear, which leads to the rotation of the cross-section. They used an example to show the analytical solutions for natural frequencies and determined the critical force for the coupled beam system. Stojanovic et al. [10] discussed the case of forced vibration of two elastically connected beams with a Winkler elastic layer in-between and the effect of an axial compression force on the amplitude ratio of system vibration for three types of external forcing (arbitrarily continuous harmonic excitation, uniformly continuous harmonic excitation and concentrated harmonic excitation). They determined general conditions of resonance and dynamic vibration absorption. Stojanovic et al. [11] discussed the analytical analysis of static stability of a system consisting of three elastically connected Timoshenko beams on an elastic foundation. They provided expressions for the critical force of the system under the influence of elastic Winkler layers. Stojanovic et al. [12] using the example of multiple elastically connected Timoshenko and Reddy-Bickford beams, determined the analytical forms of natural frequencies, their change under the effect of axial compression forces and the conditions for static stability for a different number of connected beams.
Li and Hua [13], using the spectral finite element method arrived at numerical solutions for natural frequencies of the two elastically connected Timoshenko beams with different supports. They determined vibration modes and amplitude-frequency dependence for forced vibration of the system. Also, Li et al. [14] addressed the problem of three elastically connected Timoshenko beams in their paper. They numerically determined natural frequencies for different types of support, mode shapes and the effect the stiffness of elastic inter-layers had on vibration of the system.
Ariaei et al. [15] studied the problem of a movable body according to the system of multiple elastically connected Timoshenko beams on an elastic foundation using the Transfer-matrix method. They concluded that the maximum deflection of the beam system decreases in case of a body moving on the beams closer to the surface.
Mao [16] determined mode shapes for the first ten system modes of multiple elastically connected Euler beams on an elastic foundation using the Adomian decomposition method.
Kozic et al. investigated the Lyapunov exponent and moment Lyapunov exponents of two degrees-of-freedom linear systems subjected to white noise parametric excitation [17]. The method of regular perturbation used to determine the explicit asymptotic expressions for these exponents in the presence of small intensity noises. The Lyapunov exponent and moment Lyapunov exponents are important characteristics for determining the almost-sure and moment stability of a stochastic dynamical system. As an example, they study the almost-sure and moment stability of the double-beam system under stochastic compressive axial loading. The validity of the approximate results for moment Lyapunov exponents checked by the numerical Monte Carlo simulation method for this stochastic system.
Stojanovic et al. studied the stochastic stability of the three elastically connected Euler beams on elastic foundation [18]. Stochastic stability conditions expressed by the Lyapunov exponent and moment Lyapunov exponents. The method of regular perturbation used to determine the asymptotic expressions for these exponents in the presence of small intensity noises. Analytical results presented for the almost sure and moment stability of a stochastic dynamical system. The results applied to study the moment stability of the complex structure with influence of the white noise excitation due to the axial compressive stochastic load. Also, Stojanovic et al. suggested a new -version finite element to deal with geometrically non-linear vibrations of damaged Timoshenko beams [19]. The novelty of the -element comes from the use of new displacement shape functions, which are function of the damage location and, therefore, provide for more efficient models, where accuracy improved at lower computational cost. In numerical tests in the linear regime, coupling between cross sectional rotation and longitudinal vibrations discovered, with longitudinal displacements suddenly changing direction at the damage location and with a peculiar change in the cross section rotation at the same place. Geometrically non-linear, forced vibrations then investigated in the time domain using Newmark’s method and further couplings between displacement components found.
Forced transverse vibration of a Rayleigh double-beam system with effect of compressive axial load with a Pasternak layer in-between are studied in the present paper.
2. Mathematical model
The following assumptions are considered: (a) the behavior of the beam material is linear elastic; (b) the cross-section is rigid and constant throughout the length of the beam and has one plane of symmetry; (c) shear deformations of the cross-section of the beam are considered while elastic axial deformations are ignored; (d) the equations are derived considering the geometric axial deformations; (e) the axial forces acting on the ends of the beam are not changed with time; (f) the two beams have the same effective material constants.
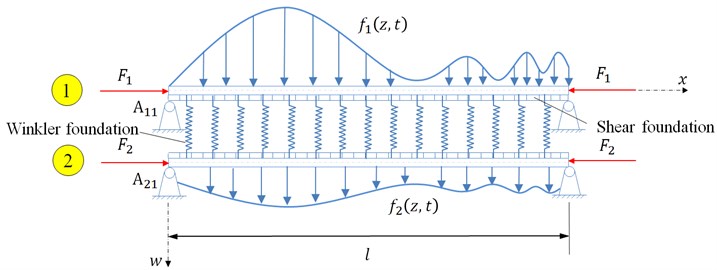
Fig. 1 shows double-beam system with Pasternak layer in-between with length of subjected to axial compressions and which are positive in compression, and arbitrarily distributed transverse continuous loads and that are positive when they act downward.
Fig. 1Double-beam complex system with a Pasternak middle layer
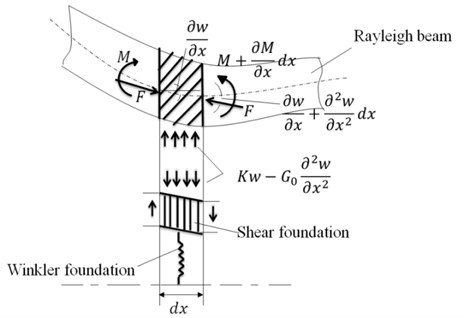
An element of deflected differential layered-beam of length with Pasternak layer between two cross-sections taken normal to the deflected axis to the beam is shown in Fig. 2.
Fig. 2Deflected differential layered-beam element with a Pasternak middle layer
The equations of forced transverse vibration of a Rayleigh double-beam system with the effect of compressive axial load with a Pasternak layer in-between have the following form:
The Eqs. (1) and (2) can be reduced to fourth-order partial differential equations for forced vibration of the Rayleigh double-beam model:
where:
The initial conditions in general form and boundary conditions for simply supported beams of the same length are assumed as follows:
3. Solution of equations
The Eqs. (3) and (4) representing forced vibrations of a Rayleigh double-beam system with Pasternak layer in-between. The natural frequencies and the corresponding mode shapes of the system should be obtained by solving the undamped free vibration with appropriate boundary conditions. Assuming time harmonic motion and using separation of variables, the solutions to Eqs. (3) and (4) with the governing boundary conditions Eq. (5) can be written in the form:
where,
Substitution of Eq. (6) into Eqs. (3), (4) yields ordinary differential equations for the Rayleigh double-beam system. Therefore:
where:
4. Forced vibration of a Rayleigh double-beam system
First we should solve the undamped free vibration of the double-beam system. Therefore:
The solutions of Eqs. (9) and (10) can be assumed to have the following forms:
Substituting Eq. (11) into Eqs. (9), (10) results in the following system of homogeneous algebraic equations for the unknown constants:
When the determinant of the coefficients in Eqs. (12), (13) vanishes, non-trivial solutions for the constants and can be obtained, which yields the following frequency (characteristic) equation:
The roots of Eq. (14) are:
where:
For each of the natural frequencies, the associated amplitude ratio of vibration modes of the two beams is given by:
Applying the classical modal expansion method, the forced vibrations of beams subjected to arbitrarily distributed continuous loads can be determined. Particular solutions of non-homogeneous differential Eqs. (3) and (4) representing forced vibrations of a Rayleigh double model can be assumed in the following:
Introduction of Eqs. (18), (19) into Eqs. (3), (4) results in:
By multiplying the Eqs. (20), (21) by the eigen-function , then integrating them with respect to from to and using orthogonality condition, we have:
where:
Now we have:
From Eqs. (17), (23), (24) after some algebraic manipulation we obtain:
From Eqs. (25), (26), we obtain:
where:
Also, and . By combining Eqs. (18), (19) and (27), the forced vibrations of an elastically connected Rayleigh double-beam system with Pasternak layer in-between can be described by:
Now these general solutions Eqs. (30) and (31) are used to find the vibrations of the two coupled Rayleigh beams.
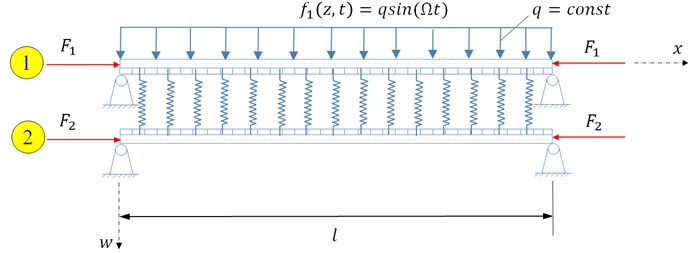
In the following, we conduct an analysis of forced vibrations for the case of uniformly distributed continuous harmonic load. For simplicity of further analysis, it is assumed that only one of the two beams is subjected to the exciting load. Without loss of generality, we suppose (see Fig. 3):
Fig. 3Double-beam complex system with the Pasternak layer in-between subjected to harmonic uniform distributed continuous load
Substituting Eq. (32) into Eqs. (28), (29), we obtain:
where:
Substituting Eqs. (33), (34) into Eqs. (30), (31) gives:
where:
Neglecting the free response, the forced vibrations of the Rayleigh double-beam system can be obtained by:
The following fundamental conditions of resonance and dynamic vibration absorption have practical significance:
1 – Resonance:
2 – Dynamic vibration absorption:
5. Numerical analysis
For simplicity, it is assumed that both beams are geometrically and physically identical:
Table 1The values of the parameters characterizing properties of the system
(m) | (N/m2) | (m2) | (N/m2) | (kg/m3) | (m4) |
10 | 1×1010 | 5×10-2 | 2×105 | 2×103 | 4×10-4 |
If the axial compressions vanish, for the Rayleigh double-beam we have:
where:
Also:
To determine the effect of compressive axial load and shear foundation modulus of Pasternak layer on the steady-state vibration amplitudes and of the system, the results under compressive axial load and those without axial load are compared. Introducing the relation:
Using non-dimensional ratio:
where, is known as the Euler load for Euler and Rayleigh beam, which is the smallest load at which the single beam ceases to be in stable equilibrium under axial compression. For the case of uniformly distributed harmonic load, the steady-state vibration amplitudes for the Rayleigh beams , , , can be determined. We accounted the results for three cases of shear foundation modulus of Pasternak layer 0, 100, 1000. If we introduce in the whole equations of this paper, we can obtain the vibration equations of the double-beam system on a Winkler elastic layer that the results are verified by comparing with those available in [12]. With the vibration mode number 3 and the exciting frequency , the effects of Pasternak layer on the steady-state vibration amplitudes and of the Rayleigh beam represented by the ratios and , shown in Figs. 4-7, respectively.
Fig. 4Relationship between ratio φ1 and parameter s for different axial compression ratio ζ and G0= 100
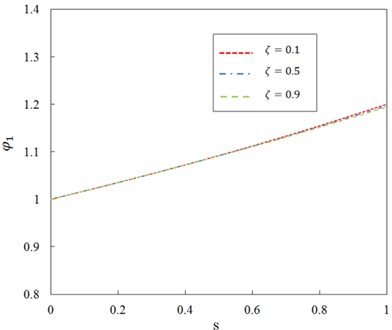
Fig. 5Relationship between ratio φ2 and parameter s for different axial compression ratio ζ and G0= 100
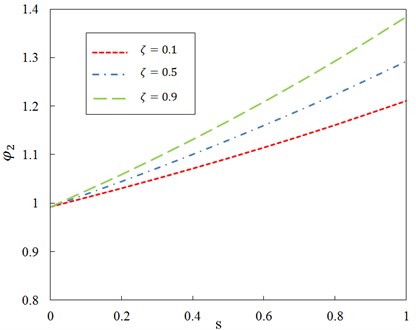
As can be seen, the ratio decreases with the increase of the axial compression, which implies that the magnitude of the steady-state vibration amplitude becomes smaller when the axial compression increases and the ratio increases with the increase of the axial compression, which implies that the magnitude of the steady-state vibration amplitude becomes larger when the axial compression increases. It can be observed that the effect of compressive axial load on the magnitude of is almost independent of the axial compression ratio of the two beams whereas it is significantly dependent on the magnitude of .
Fig. 6Relationship between ratio φ1 and dimensionless parameter s for different shear foundation modulus of Pasternak layer and ζ= 0.5
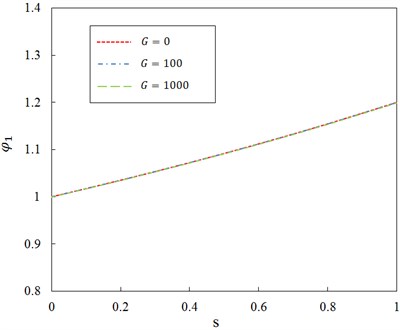
Fig. 7Relationship between ratio φ2 and dimensionless parameter s for different shear foundation modulus of Pasternak layer and ζ= 0.5
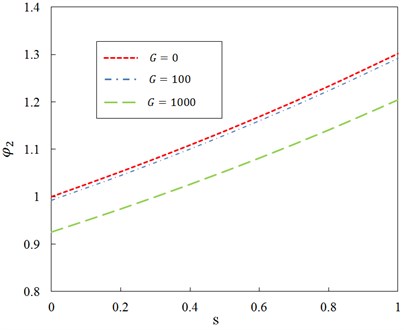
Table 2Effects of shear foundation modulus of Pasternak layer on the steady-state vibration amplitudes ratios φ1 and φ2 for different compressive axial ratio ζ
1 | 0.8 | 0.6 | 0.4 | 0.2 | 0 | |
1.1999 | 1.1544 | 1.112 | 1.0723 | 1.0351 | 1 | |
1.1998 | 1.1543 | 1.1119 | 1.0723 | 1.035 | 0.9999 | |
1.1987 | 1.1533 | 1.111 | 1.0715 | 1.0343 | 0.9993 | |
1.1965 | 1.1526 | 1.1112 | 1.0722 | 1.0351 | 1 | |
1.1963 | 1.1525 | 1.1111 | 1.0721 | 1.0351 | 0.9999 | |
1.1952 | 1.1515 | 1.1102 | 1.0713 | 1.0343 | 0.9993 | |
1.194 | 1.1513 | 1.1107 | 1.072 | 1.0352 | 1 | |
1.1938 | 1.1512 | 1.1106 | 1.072 | 1.0351 | 0.9999 | |
1.1927 | 1.1501 | 1.1097 | 1.0711 | 1.0344 | 0.9993 | |
1.22 | 1.1699 | 1.1232 | 1.0796 | 1.0386 | 1 | |
1.2108 | 1.1611 | 1.1147 | 1.0714 | 1.0308 | 0.9925 | |
1.1287 | 1.0824 | 1.0393 | 0.999 | 0.9611 | 0.9255 | |
1.302 | 1.2332 | 1.169 | 1.109 | 1.0528 | 1 | |
1.2921 | 1.2238 | 1.1602 | 1.1006 | 1.0448 | 0.9925 | |
1.2044 | 1.1408 | 1.0816 | 1.0261 | 0.9742 | 0.9255 | |
1.3944 | 1.3028 | 1.2181 | 1.1398 | 1.0673 | 1 | |
1.3839 | 1.2929 | 1.2089 | 1.1312 | 1.0592 | 0.9925 | |
1.2897 | 1.2051 | 1.1269 | 1.0546 | 0.9876 | 0.9255 | |
As we said before in this paper the effects of Pasternak layer on forced transverse vibration of a Rayleigh double-beam system with effect of compressive axial load is analyzed. Effects of Pasternak layer cannot be observed in Figs. 4-7. Numerical values of the ratios and for different shear foundation modulus of Pasternak layer with different axial compression ratio of the two beams is shown in Table 2. Numerical results of the ratios and show that the difference with ratios and decrease with the increase of shear modulus of the Pasternak layer for different axial compression ratio , but It can be observed that the effect of shear foundation modulus of Pasternak layer on the magnitude of is almost independent of the axial compression ratio of the two beams whereas it is significantly dependent on the magnitude of .
Fig. 8Relationship between ratio φ1 and dimensionless parameter s for different mode number n and G0= 100
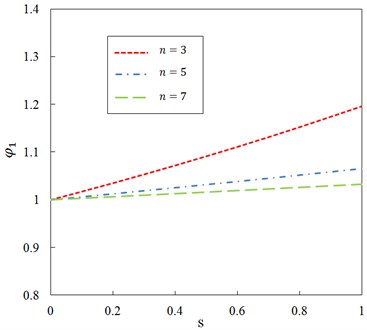
Fig. 9Relationship between ratio φ2 and dimensionless parameter s for different mode number n and G0= 100
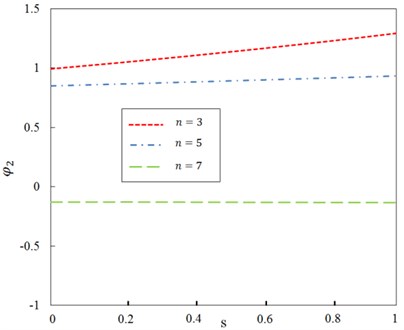
Fig. 10Relationship between ratio φ1 and dimensionless parameter s for different shear modulus of Pasternak (n= 5)
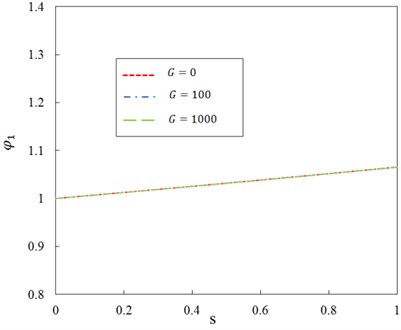
Fig. 11Relationship between ratio φ2 and dimensionless parameter s for different shear modulus of Pasternak (n=5)
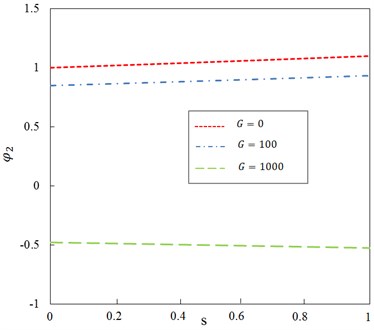
On the other hand, with the axial compression ratio and the exciting frequency , the effects of Pasternak layer on the steady-state vibration amplitudes and are shown in Figs. 8-11 for different mode shape number , respectively. It can be seen that, with the same axial compression, the ratios and diminish with the increasing vibration mode number , which implies that the magnitudes of the steady-state vibration amplitudes and get smaller when the vibration mode number becomes larger.
Table 3 shows the effects of compressive axial load and shear modulus of Pasternak layer on difference between the steady-state vibration amplitudes ratios and of the Rayleigh beam for different mode number . It can be observed that the differences between ratios and of the Rayleigh beam increase with increasing the dimensionless parameter . Also we can see that the ratios and decrease with increasing of the shear foundation modulus of Pasternak layer for different mode shape numbers.
Table 3Effects of shear foundation modulus of Pasternak layer on the steady-state vibration amplitudes ratios φ1 and φ2 for different mode shape number n
1 | 0.8 | 0.6 | 0.4 | 0.2 | 0 | |
1.1965 | 1.1526 | 1.1112 | 1.0722 | 1.0351 | 1 | |
1.1963 | 1.1525 | 1.1111 | 1.0721 | 1.0351 | 0.9999 | |
1.1952 | 1.1515 | 1.1102 | 1.0713 | 1.0343 | 0.9993 | |
1.0654 | 1.0518 | 1.0385 | 1.0254 | 1.0126 | 1 | |
1.0654 | 1.0518 | 1.0384 | 1.0254 | 1.0125 | 1 | |
1.065 | 1.0514 | 1.038 | 1.0250 | 1.0123 | 0.9998 | |
1.0327 | 1.026 | 1.0194 | 1.0129 | 1.0064 | 1 | |
1.0327 | 1.026 | 1.0194 | 1.0128 | 1.0064 | 1 | |
1.0324 | 1.0258 | 1.0192 | 1.0127 | 1.0063 | 0.9999 | |
1.302 | 1.2332 | 1.169 | 1.109 | 1.0528 | 1 | |
1.2921 | 1.2238 | 1.1602 | 1.1006 | 1.0448 | 0.9925 | |
1.2044 | 1.1408 | 1.0816 | 1.0261 | 0.9742 | 0.9255 | |
1.0992 | 1.0784 | 1.0581 | 1.0382 | 1.0189 | 1 | |
0.9331 | 0.9154 | 0.8982 | 0.8814 | 0.8649 | 0.8489 | |
–0.5249 | –0.515 | –0.5053 | –0.4959 | –0.4867 | –0.4777 | |
1.0493 | 1.0392 | 1.0292 | 1.0193 | 1.0096 | 1 | |
–0.1343 | –0.133 | –0.1318 | –0.1305 | –0.1292 | –0.1280 | |
–10.2863 | –10.1877 | –10.0903 | –9.9940 | –9.8988 | –9.8047 | |
6. Conclusions
In vibration analysis, a dynamic vibration absorber, such as Rayleigh double beam system, reduces or eliminates the vibration of a harmonically excited system. Rotating machines such as engines, motors, and pumps often incite vibration due to rotational imbalances. A dynamic absorber can be affixed to the rotating machine and tuned to oscillate in such a way that exactly counteracts the force from the rotating imbalance. This reduces the possibility that a resonance condition will occur, which can cause rapid catastrophic failure. Properly implemented, a dynamic absorber will neutralize the undesirable vibration, which would otherwise reduce service life or cause mechanical damage. Based on the Rayleigh beam theory, the forced transverse vibration of an elastically connected simply supported Rayleigh double-beam, with a Pasternak interlayer under compressive axial loading for one case of particular excitation loading are studied. The dynamic response of the system caused by arbitrarily distributed continuous loads is obtained. The magnitudes of the steady-state vibration amplitudes of the beam are dependent on the axial compression and shear foundation modulus of Pasternak layer. Also we concluded that the ratios and decrease with increasing of the shear foundation modulus of Pasternak layer . Founded analytical forms can be used in the optimal design of a new type of a dynamic vibration absorber. Thus the Rayleigh beam-type dynamic absorber with Pasternak layer in-between can be applied to suppress the excessive vibrations of corresponding beam systems and be more effective than the double-beam system with a Winkler elastic layer. The beam-type dynamic damper is an accepted concept for a Continuous Dynamic Vibration Absorber (CDVA).
References
-
Seelig J. M., Hoppmann W. H. Impact on an elastically connected double-beam system. Transactions of the American Society of Mechanical Engineers, Journal of Applied Mechanics, Vol. 31, 1964, p. 621-626.
-
Oniszczuk Z. Free transverse vibrations of elastically connected simply supported double-beam complex system. Journal of Sound and Vibration, Vol. 232, Issue 2, 2000, p. 387-403.
-
Oniszczuk Z. Forced transverse vibrations of an elastically connected complex simply supported double-beam system. Journal of Sound and Vibration, Vol. 264, Issue 2, 2003, p. 273-286.
-
Zhang Y. Q., Lu Y., Wang S. L., Liu X. Vibration and buckling of a double-beam system under compressive axial loading. Journal of Sound and Vibration, Vol. 318, Issue 1, 2008, p. 341-352.
-
Zhang Y. Q., Lu Y., Ma G. W. Effect of compressive axial load on forced transverse vibrations of a double-beam system. International Journal of Mechanical Sciences, Vol. 50, Issue 2, 2008, p. 299-305.
-
Pasternak P. L. On a New Method of Analysis of an Elastic Foundation by Means of Two Foundation Constants. Moscow, 1954.
-
Wang T. W., Stephens J. E. Natural frequencies of Timoshenko beams on Pasternak foundations. Journal of Sound and Vibration, Vol. 51, Issue 2, 1977, p. 149-155.
-
De Rosa M. A. Free vibrations of Timoshenko beams on two-parameter elastic foundation. Computers and Structures, Vol. 57, Issue 1, 1995, p. 151-156.
-
Stojanovic V., Kozic P., Pavlovic R., Janevski G. Effect of rotary inertia shear on vibration and buckling of a double beam system under compressive axial loading. Archive of Applied Mechanics, Vol. 81, Issue 12, 2011, p. 1993-2005.
-
Stojanovic V., Kozic P., Janevski G. Buckling instabilities of elastically connected Timoshenko beams on an elastic layer subjected to axial forces. Journal of Mechanics of Materials and Structures, Vol. 7, Issue 4, 2012, p. 363-374.
-
Stojanovic V., Kozic P. Forced transverse vibration of Rayleigh and Timoshenko double-beam system with effect of compressive axial load. International Journal of Mechanical Sciences, Vol. 60, Issue 1, 2012, p. 59-71.
-
Stojanovic V., Kozic P., Janevski G. Exact closed-form solutions for the natural frequencies and stability of elastically connected multiple beam system using Timoshenko and high-order shear deformation theory. Journal of Sound and Vibration, Vol. 332, Issue 3, 2013, p. 563-576.
-
Li J., Hua H. Spectral finite element analysis of elastically connected double-beam systems. Finite Elements in Analysis and Design, Vol. 43, Issue 15, 2007, p. 1155-1168.
-
Li J., Chen Y., Hua H. Exact dynamic stiffness matrix of a Timoshenko three-beam system. International Journal of Mechanical Sciences, Vol. 50, Issue 6, 2008, p. 1023-1034.
-
Ariaei A., Ziaei-Rad S., Ghayour M. Transverse vibration of a multiple-Timoshenko beam system with intermediate elastic connections due to a moving load. Archive of Applied Mechanics, Vol. 81, Issue 3, 2011, p. 263-281.
-
Mao Q. Free vibration analysis of elastically connected multiple-beams by using the Adomian modified decomposition method. Journal of Sound and Vibration, Vol. 331, Issue 11, 2012, p. 2532-2542.
-
Kozic P., Janevski G., Pavlovic R. Moment Lyapunov exponents and stochastic stability of a double-beam system under compressive axial loading. International Journal of Solids and Structures, Vol. 47, Issue 10, 2010, p. 1435-1442.
-
Stojanovic V., Petkovic M. Moment Lyapunov exponents and stochastic stability of a three dimensional system on elastic foundation using a perturbation approach. Journal of Applied Mechanics, Vol. 80, Issue 5, 2013, p. 051009.
-
Stojanovic V., Ribeiro P., Stoykov S. Non-linear vibration of Timoshenko damaged beams by a new ρ-version finite element method. Computers and Structurers, Vol. 120, 2013, p. 107-119.
