Uncertainty of measurement of eigenfrequency using a dynamically directed vibroexciter

Sudintas, A.; Paškevičius, P.; Patašienė, L.; Ragulskis, L.

Journal of Measurements in Engineering

Browse Journal

Submit article

Published: 30 June 2015

Check for updates

Uncertainty of measurement of eigenfrequency using a dynamically directed vibroexciter

A. Sudintas¹

P. Paškevičius²

L. Patašienė³

L. Ragulskis⁴

^{1, 2, 3}Kaunas University of Technology, Kaunas, Lithuania

⁴Vytautas Magnus University, Kaunas, Lithuania

Corresponding Author:

A. Sudintas

Cite the article Download PDF

Downloads 1066

Abstract

Measurement of eigenfrequency using a dynamically directed vibroexciter is investigated. Lyapunov indicators are calculated for various values of parameters of the system. It is shown that when the frequency of excitation coincides with the eigenfrequency there is a positive Lyapunov indicator. Thus chaotic motion takes place and causes uncertainty in the measurement of eigenfrequency.

1. Introduction

Measurement of eigenfrequency using a dynamically directed vibroexciter is investigated. Lyapunov indicators are calculated for various values of parameters of the system. Calculation of Lyapunov indicators is based on the material presented in [1, 2].

It is shown that when the frequency of excitation coincides with the eigenfrequency there is a positive Lyapunov indicator. Thus chaotic motion takes place and causes uncertainty in the measurement of eigenfrequency. Related problems of chaotic motion are investigated in [3-5].

2. Model of the system

The system is described by the following equation:

1

[M] \{\ddot{δ}\} + [C] \{\dot{δ}\} + [K] \{δ\} = \{F\},

where the upper dot denotes differentiation with respect to time and:

2

[M] = [\begin{matrix} 1 + μ & μ z c o s α \\ μ z c o s α & μ z^{2} \end{matrix}],

3

[C] = [\begin{matrix} h_{y} & 2 μ \dot{z} c o s α - μ z \dot{α} s i n α \\ 0 & h_{α} + 2 μ z \dot{z} \end{matrix}],

4

[K] = [\begin{array}{l} p_{y}^{2} & 0 \\ 0 & 0 \end{array}],

5

\{F\} = \{\begin{matrix} - μ \ddot{z} s i n α \\ - μ z g c o s α \end{matrix}\},

6

z = A c o s ω t,

7

\{δ\} = \{\begin{array}{l} y \\ α \end{array}\},

where $y$ and $α$ are the generalized coordinates, $A$ is the amplitude of excitation, $ω$ is the frequency of excitation, $μ$ is the inertial parameter of the system, $h_{y}$ and $h_{α}$ are the damping parameters of the system, $p_{y}$ is the stiffness parameter of the system, g is the acceleration of gravity, $t$ is time.

The following initial conditions are assumed:

8

\{δ (0)\} = \{\begin{array}{l} 0 \\ \frac{π}{4} \end{array}\},

9

\{\dot{δ} (0)\} = \{\begin{array}{l} 0 \\ 0 \end{array}\} .

3. Procedure of calculation of Lyapunov indicators

The linearized system is described by the following equation:

10

[\bar{M}] \{\ddot{\bar{δ}}\} + [\bar{C}] \{\dot{\bar{δ}}\} + [\bar{K}] \{\bar{δ}\} = \{\bar{F}\},

where:

11

[\bar{M}] = [\begin{matrix} 1 + μ & μ z c o s α \\ μ z c o s α & μ z^{2} \end{matrix}],

12

[\bar{C}] = [\begin{matrix} h_{y} & 2 μ \dot{z} c o s α - 2 μ z \dot{α} s i n α \\ 0 & h_{α} + 2 μ z \dot{z} \end{matrix}],

13

[\bar{K}] = [\begin{matrix} p_{y}^{2} & - μ z \ddot{α} s i n α - 2 μ \dot{z} \dot{α} s i n α - μ z {\dot{α}}^{2} c o s α + μ \ddot{z} c o s α \\ 0 & - μ z \ddot{y} s i n α - μ z g s i n α \end{matrix}],

14

\{\bar{F}\} = \{\begin{array}{l} 0 \\ 0 \end{array}\},

15

\{\bar{δ}\} = \{\begin{array}{l} d y \\ d α \end{array}\},

where $d$ denotes differential.

The following four initial conditions are assumed:

16

[\begin{array}{l} \{{\bar{δ}}^{(1)} (0)\} & \{{\bar{δ}}^{(2)} (0)\} & \{{\bar{δ}}^{(3)} (0)\} & \{{\bar{δ}}^{(4)} (0)\} \end{array}] = [\begin{array}{l} \{\begin{array}{l} 1 \\ 0 \end{array}\} & \{\begin{array}{l} 0 \\ 1 \end{array}\} & \{\begin{array}{l} 0 \\ 0 \end{array}\} & \{\begin{array}{l} 0 \\ 0 \end{array}\} \end{array}],

17

[\begin{array}{l} \{{\dot{\bar{δ}}}^{(1)} (0)\} & \{{\dot{\bar{δ}}}^{(2)} (0)\} & \{{\dot{\bar{δ}}}^{(3)} (0)\} & \{{\dot{\bar{δ}}}^{(4)} (0)\} \end{array}] = [\begin{array}{l} \{\begin{array}{l} 0 \\ 0 \end{array}\} & \{\begin{array}{l} 0 \\ 0 \end{array}\} & \{\begin{array}{l} 1 \\ 0 \end{array}\} & \{\begin{array}{l} 0 \\ 1 \end{array}\} \end{array}],

where number in the superscript denotes which initial condition is represented.

In the step $i$ for Lyapunov indicator $j =$ 1, 2, 3, 4 the following calculations are performed:

18

s_{k} = {\{{\bar{δ}}^{(j)}\}}^{T} \{{\bar{δ}}^{(k)}\} + {\{{\dot{\bar{δ}}}^{(j)}\}}^{T} \{{\dot{\bar{δ}}}^{(k)}\}, k = 1, \dots, j - 1,

19

\{\begin{array}{l} \{{\bar{δ}}^{(j)}\} : = \{{\bar{δ}}^{(j)}\} - \sum_{k = 1}^{j - 1} s_{k} \{{\bar{δ}}^{(k)}\}, \\ \{{\dot{\bar{δ}}}^{(j)}\} : = \{{\dot{\bar{δ}}}^{(j)}\} - \sum_{k = 1}^{j - 1} s_{k} \{{\dot{\bar{δ}}}^{(k)}\}, \end{array}

20

d_{i}^{(j)} = \sqrt{{\{{\bar{δ}}^{(j)}\}}^{T} \{{\bar{δ}}^{(j)}\} + {\{{\dot{\bar{δ}}}^{(j)}\}}^{T} \{{\dot{\bar{δ}}}^{(j)}\}},

21

\{\begin{array}{l} \{{\bar{δ}}^{(j)}\} : = \frac{1}{d_{i}^{(j)}} \{{\bar{δ}}^{(j)}\}, \\ \{{\dot{\bar{δ}}}^{(j)}\} : = \frac{1}{d_{i}^{(j)}} \{{\dot{\bar{δ}}}^{(j)}\}, \end{array}

where $: =$ denotes the assignment operator.

Lyapunov indicator is determined from:

22

λ_{j} T = \sum_{i = 1}^{m} l n d_{i}^{(j)},

where $λ_{j}$ is the Lyapunov indicator, $T$ is time of integration, $m$ is the number of time steps.

4. Numerical results of investigations

The following parameters of the investigated system are assumed: $A =$ 0.01, $μ =$ 0.3, $h_{y} =$ 0.2, $p_{y} =$ 20π, $h_{α} =$ 0.2, $g =$ 9.81.

Fig. 1λ1, λ2, λ3, λ4 as functions of time when ω= 10π

Fig. 2λ1, λ2, λ3, λ4 as functions of time when ω= 15π

4.1. Low frequency excitation

Lyapunov indicators as functions of time when $ω =$ 10 $π$ are presented in Fig. 1 and when $ω =$ 15 $π$ are presented in Fig. 2.

From the presented results it is seen that all Lyapunov indicators are negative. Thus there is no chaotic motion and measurements can be performed.

4.2. High frequency excitation

Lyapunov indicators as functions of time when $ω =$ 25 $π$ are presented in Fig. 3, when $ω =$ 30 $π$ are presented in Fig. 4 and when $ω =$ 40 $π$ are presented in Fig. 5.

Fig. 3λ1, λ2, λ3, λ4 as functions of time when ω= 25π

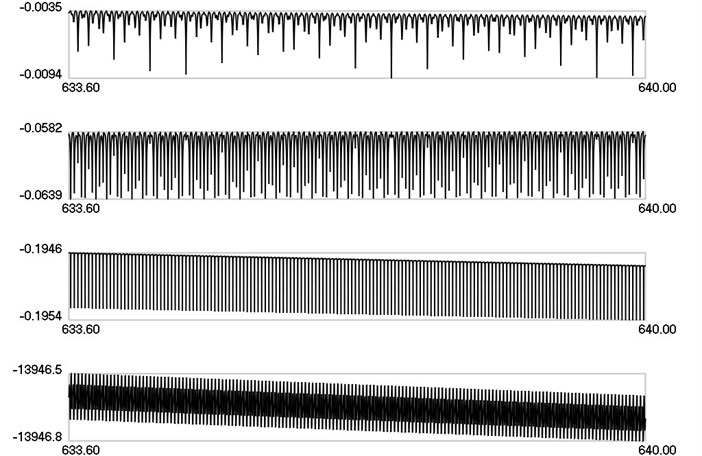
Fig. 4λ1, λ2, λ3, λ4 as functions of time when ω= 30π

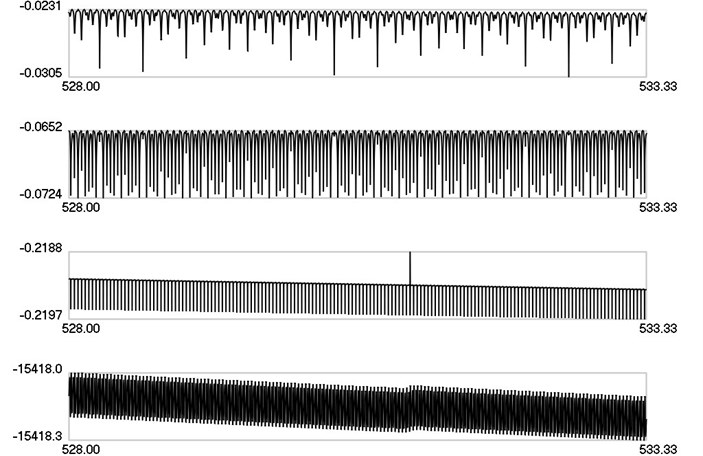
Fig. 5λ1, λ2, λ3, λ4 as functions of time when ω= 40π

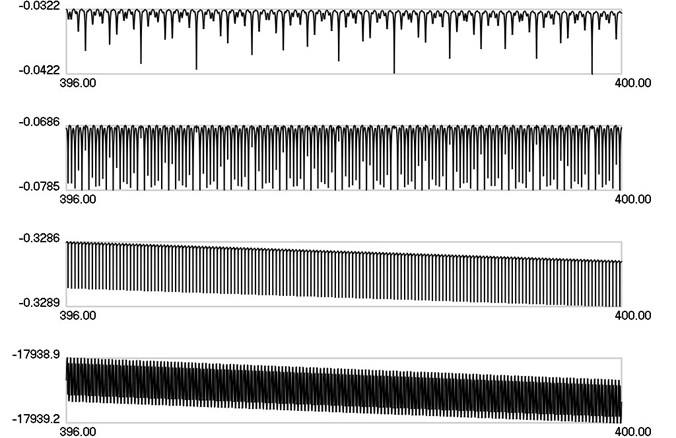
From the presented results it is seen that all Lyapunov indicators are negative. Thus there is no chaotic motion and measurements can be performed.

4.3. Chaotic excitation

Lyapunov indicators as functions of time when $ω =$ 20 $π$ are presented in Fig. 6.

Fig. 6λ1, λ2, λ3, λ4 as functions of time when ω= 20π

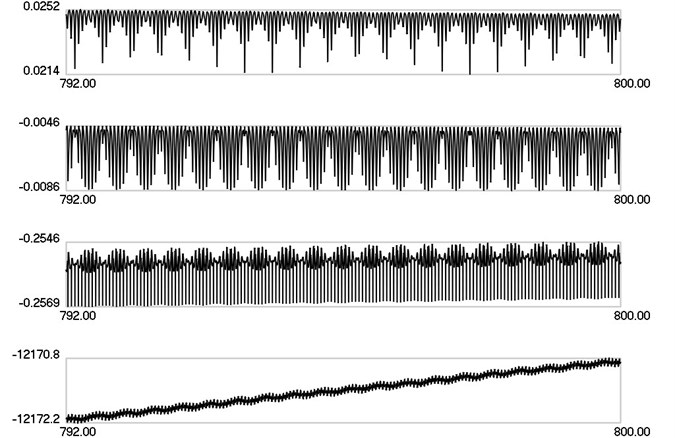
From the presented results it is seen that the first Lyapunov indicator is positive. Thus there is chaotic motion and it causes uncertainty in the measurements.

5. Uncertainty of measurement of eigenfrequency

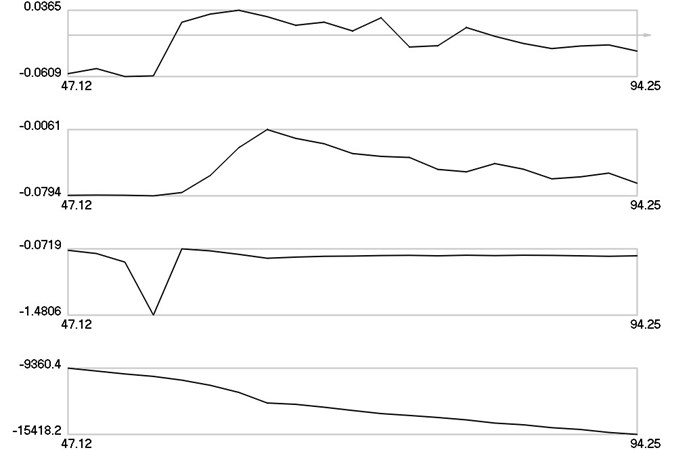
Lyapunov indicators as functions of frequency of excitation in the interval from $ω =$ 15 $π$ to $ω =$ 30 $π$ are presented in Fig. 7.

From the presented results the interval where the first Lyapunov indicator is positive is approximately seen. In this interval there is chaotic motion and it causes uncertainty in the measurements.

Fig. 7λ1, λ2, λ3, λ4 as functions of frequency of excitation

6. Conclusions

Measurement of eigenfrequency using a dynamically directed vibroexciter is investigated. Lyapunov indicators are calculated for various values of parameters of the system. Low frequency excitations and high frequency excitations are investigated. From the presented results it is seen that all Lyapunov indicators in both cases are negative. Thus there is no chaotic motion and measurements can be performed.

It is shown that when the frequency of excitation coincides with the eigenfrequency there is a positive Lyapunov indicator. Thus chaotic motion takes place and it causes uncertainty in the measurement of eigenfrequency. This fact reduces the precision of the measurement procedure.

Lyapunov indicators as functions of frequency of excitation are obtained. From the presented results the frequency interval where the first Lyapunov indicator is positive is approximately seen. In this interval there is chaotic motion and it causes uncertainty in the measurements of eigenfrequency.

References

Neymark Yu. I., Landa P. S. Stochastic and Chaotic Vibrations. Nauka, Moscow, 1987, (in Russian).

Search CrossRef
Dmitriev A. S., Kislov V. Ya. Chaotic Oscillations in Radiophysics and Electronics. Nauka, Moscow, 1989, (in Russian).

Search CrossRef
Zaslavsky G. M., Sagdeev R. Z., Usikov D. A., Chernikov A. A. Weak Chaos and Quasi – Regular Patterns. Nauka, Moscow, 1991, (in Russian).

Search CrossRef
Awrejcewicz J., Krysko V. A. Chaos in Structural Mechanics. Springer, Berlin, 2008.

Search CrossRef
Ueda Y. The Road to Chaos – II. Aerial Press, Santa Cruz, 2001.

Search CrossRef

About this article

Received

20 March 2015

Accepted

23 June 2015

Published

30 June 2015

Keywords

uncertainty of measurement

vibroexciter

dynamical directivity

eigenfrequency

Lyapunov indicator

chaos

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.