Abstract
A novel method combining max-min approach (MMA) with energy method is proposed for the derivation of the approximate analytical solution for shock response of the strong nonlinear system. MMA is used to evaluate the governing differential equation with nonlinearity terms and to obtain the approximate solution. The maximum shock response displacement of the system is obtained by energy method, and then the approximation solution by MMA is corrected. Three examples are given to illustrate the validity of the method. It is shown that the corrected MMA method always lead to a better approximate solution for different kinds of nonlinear problems. The results provides a new simple but effective method for the analysis of shock response of strong nonlinear problems.
1. Introduction
There are various kinds of nonlinear problems in the engineering field. In most cases, the constitutive relations of systems are strong nonlinear, which are usually difficult to be solved analytically. Various analytical approaches for solving nonlinear differential equations are proposed and applied in the analysis of some engineering problems, such as the homotopy analysis method [1-3], variational iteration method (VIM) [4-6], the method of harmonic balance [7-9], Adomian’s decomposition method [10-12], parameter expansion method [13-15] and max-min approach (MMA) [16-18]. Among these analytical methods, as suggested by S. S. Ganji [19] and Zeng [20], MMA is very effective for solving nonlinear oscillators.
The shock response is very different from free vibration for nonlinear systems. By combining the L-P Perturbation Method with the energy method (EM) and combining the VIM with the EM, Xiang [21] and Chen [22] get good analytical expressions of dropping shock response of nonlinear packaging systems separately. In this study, the shock response of strongly nonlinear systems is considered, and the correction method combining the approximate solution of system applying the MMA with the EM is developed.
2. MMA and EM
2.1. Basic idea of the MMA [17]
Considering the following equation:
where is a nonnegative function. A trial-function is chosen in the following form:
where is the frequency to be determined.
Observing that the square of frequency , has:
Hence, it follows that:
According to He Chengtian’s interpolation [23, 24], one can have:
where, and are weighting factors, and .
So the frequency can be approximated as:
Then, one can get the approximate solution for Eq. (1) as:
where, can be easily obtained.
2.2. Basic idea of the EM
For nonlinear system without damping, the kinetic energy of the system transforms into completely elastic potential energy when the deformation of the material achieves the maximum value, . Assuming the critical impact velocity of the system is , the critical kinetic energy of the system can be written as:
For a nonlinear system, denotes the corresponding restoring force, where is a nonlinear function of , depending upon only the function of x. By using the energy method (EM), one can have:
The maximum deformation can be obtained by solving Eq. (9).
3. Correction method of MMA
3.1. Example 1
Considering the duffing system, the governing equation can be written as:
where the dot denotes the differentiation with respect to the time , is the mass of product, is the displacement of the system, and denote the constant coefficient, respectively, and is the critical impact velocity. The restoring force of the system can be represented as:
By introducing parameters , , and setting and , one can obtain the dimensionless equation as:
where the prime denotes the differentiation with respect to the . To apply MMA for solving Eq. (12), Eq. (12) is firstly re-written in the following form:
One can choose a trial-function in the form:
where is the frequency to be determined.
Observing that the square of frequency, , one can have:
Hence, it follows that:
According to He Chengtian’s interpolation [21, 22], one can have:
where and are weighting factors, .
So the frequency can be approximated as:
Then, we get the approximate solution of Eq. (12) as:
Combination of Eq. (12) and Eq. (19) leads to:
If, by chance, Eq. (19) is the exact solution, then the right hand side of Eq. (20) is vanishing completely. Since our approach is only an approximation to the exact solution, we set:
where . Substituting Eq. (19) into Eq. (21), one can obtain:
Finally the frequency can be obtained as:
And the approximate solution of the dimensionless equation by MMA can be written as:
It is easy for one to get the approximate solution of the original Eq. (10) in the form:
where is the frequency of the original system. The exact frequency reads:
The velocity response of the system can be expressed as:
From Eq. (28), one can obtain:
Combining Eq. (10) and Eq. (29), the parameter is obtained. Substituting it into Eq. (26), one can get the value of frequency .
When:
substituting it into Eq. (24), one can obtain:
A new method, namely, the corrected MMA (CMMA) is suggested here to obtain a better solution to nonlinear equation, which integrates the MMA with the EM. According to the EM, one have:
The exact maximum displacement is obtained as:
Combining Eq. (25), Eq. (30) and Eq. (32), the corrected solution is obtained as:
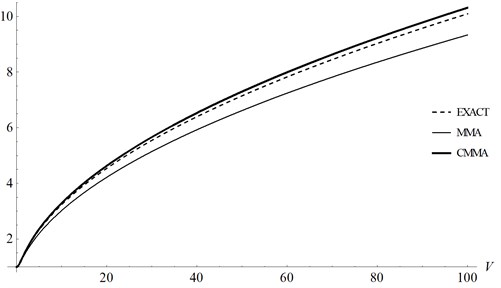
To illustrate the validity of CMMA for this example, the comparison of results obtained by MMA and CMMA is given in Table 1 and Fig. 1. It is shown that the CMMA tends to give a more precise result than MMA for nonlinear equation.
Table 1Comparison of frequency corresponding to various parameters of system for Example 1
0.01 | 0.1 | 1.0 | 10.0 | 100.0 | |
1.0000019 | 1.0037230 | 1.2413297 | 3.2403053 | 10.0914601 | |
1.0000375 | 1.0037153 | 1.2247449 | 3.0289727 | 9.3329515 | |
1.0000375 | 1.0037245 | 1.2446036 | 3.2989521 | 10.3110945 | |
0.0000356 | 0.0000077 | 0.0133605 | 0.0652200 | 0.0751634 | |
0.0000356 | 0.0000015 | 0.0026374 | 0.0180992 | 0.0217644 | |
3.2. Example 2
The dynamic equation of this example is shown in Eq. (35):
Similarly, here the dot denotes the differentiation with respect to the time , is the mass of product, is the displacement of the system, and denote the constant coefficient, respectively, and is the critical impact velocity. The restoring force of the system can be represented as:
Fig. 1Comparison of MMA and CMMA with the exact solution for Example 1
By introducing parameters , , and setting and , one can obtain the dimensionless equation and initial conditions of system as following:
where the prime denotes the differentiation with respect to the .
Eq. (37) can be rewritten in the following form:
By using as a trial function, the maximal and minimal values of are, respectively, 1 and , so one can immediately obtain:
According to MMA, one can have:
where and are weighting factors, .
So the frequency can be approximated as:
Now re-write Eq. (37) in the form:
Setting:
one can obtain:
The approximate frequency can be obtained as:
And the approximate solution of the dimensionless equation by MMA can be written as:
Similarly, it is easy for one to get the approximate solution of the original Eq. (35) in the form:
where is the frequency of the original system. Its exact frequency reads:
The velocity response of the system can be expressed as:
From Eq. (50), one can obtain:
Combining Eq. (35) and Eq. (51), the parameter is obtained. Substituting it into Eq. (48), one can get the value of frequency .
When:
substituting it into Eq. (47), one can obtain:
By using the EM, we have:
Then, the exact maximum displacement is obtained as:
Combining Eq. (47), Eq. (52) and Eq. (54), the corrected solution is obtained as:
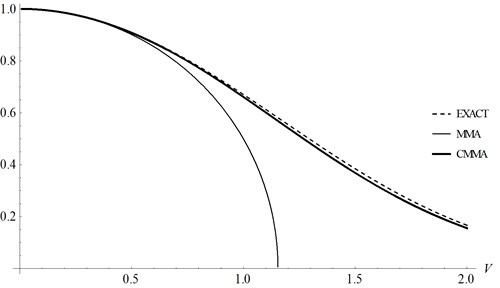
To illustrate the validity of CMMA for this example, comparison of results is given in Table 2 and Fig. 2. It is shown that CMMA is still effective when MMA fails.
Table 2Comparison of frequency corresponding to various parameters of system for Example 2
0.01 | 0.1 | 0.5 | 1.0 | 2.0 | |
0.9999626 | 0.9962557 | 0.9089836 | 0.6702093 | 0.1667291 | |
0.9999625 | 0.9962429 | 0.9013878 | 0.50 | – | |
0.9999625 | 0.9962524 | 0.9079589 | 0.6610046 | 0.1557969 | |
0.0000001 | 0.0000128 | 0.0083564 | 0.2539644 | – | |
0.0000001 | 0.0000033 | 0.0011273 | 0.0137341 | 0.0655686 | |
Fig. 2Comparison of MMA and CMMA with the exact solution for Example 2
3.3. Example 3
Considering the following example:
where the dot denotes the differentiation with respect to the time , is the mass of product, is the displacement of the system, and denote the constant coefficient, respectively, and is the critical impact velocity. The restoring force of the system can be represented as:
By introducing parameters , , and setting and , one can obtain the dimensionless equation and initial conditions of system as following forms:
where the prime denotes the differentiation with respect to the .
By using as a trial function, one can write:
According to the MMA, one can have:
where and are weighting factors, .
The frequency can be approximated as:
Now re-write Eq. (59) in the following form:
Setting:
one can obtain:
The approximate frequency can be obtained as:
And the approximate solution of the dimensionless equation by MMA can be written as:
The approximate solution of the original Eq. (56) can be obtained in the form:
where is the frequency of the original system.
The velocity response of the system can be expressed as:
From Eq. (70), one can obtain:
Combining Eq. (56) and Eq. (70), the parameter is obtained. Substituting it into Eq. (68), one can get the value of frequency .
When:
substituting it into Eq. (68), one can obtain:
By using the EM, we have:
Note that the maximum displacement, , is approximated by EM in this case.
The approximate maximum displacement by EM is obtained as:
Combining Eq. (48), Eq. (72) and Eq. (74), the corrected solution is obtained as:
The exact frequency cannot be obtained for this example. We showed comparison of in Figs. 3(a)-(d). These figures are related to parameters 1, 0.01, 1, , 1, and 1, , respectively. It is shown that the CMMA can give a more precise result than MMA for the nonlinear problem although the exact maximum displacement response cannot be obtained by the EM.
Fig. 3Comparison of x(t) in case of m=e=f=1 for Example 3 (Solid line: CMMA; Dash-dotted line: MMA; Symbols: Runge-Kutta)
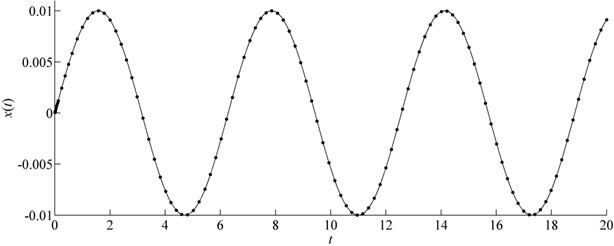
a)
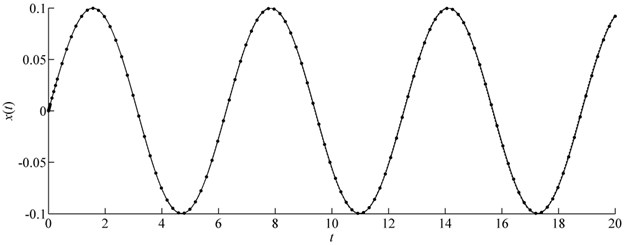
b)
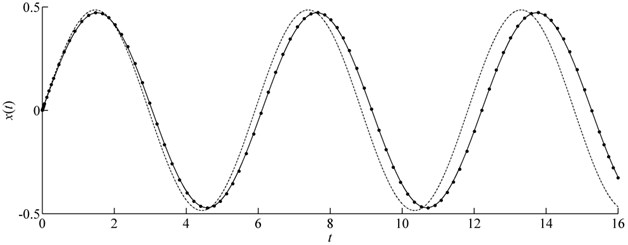
c)
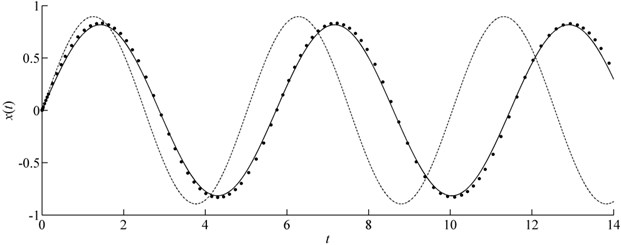
d)
4. Conclusion
In this paper, the max-min approach (MMA) which is widely applied for various kinds of nonlinear equations is combined with energy method (EM), a new technique called CMMA is proposed and applied to analysis the shock response of strongly nonlinear system.
Three examples were given to illustrate the validity of the method. The first one shows CMMA is better than MMA for strongly nonlinear system. And it can be seen that CMMA is still effective when the MMA fails from the second example. Although sometimes the exact maximum displacement response cannot be obtained by the EM, the approximate solution is better by CMMA and closed to the numerical solution.
Overall, it can be concluded that CMMA has a great application respect in strong nonlinear problems.
References
-
Liao Shijun On the homotopy analysis method for nonlinear problems. Applied Mathematics and Computation, Vol. 147, Issue 2, 2004, p. 499-513.
-
Zou Li, Zong Zhi, Wang L, et al. Solving the discrete KdV equation with homotopy analysis method. Physics Letters A, Vol. 370, Issue 3, 2007, p. 287-294.
-
Liao Shi-jun Homotopy Analysis Method in Nonlinear Differential Equations. Springer, London, 2012, p. 26-38.
-
He Ji-huan, Wu Xu-hong Variational iteration method: new development and applications. Computers and Mathematics with Applications, Vol. 54, 2007, p. 881-894.
-
Guo-cheng Wu, Dumitru Baleanu Variational iteration method for the Burgers’ flow with fractional derivatives-new Lagrange multipliers. Applied Mathematical Modelling, Vol. 37, Issue 9, 2013, p. 6183-6190.
-
Khader M. M. Numerical and theoretical treatment for solving linear and nonlinear delay differential equations using variational iteration method. Arab Journal of Mathematical Sciences, Vol. 19, Issue 2, 2013, p. 243-256.
-
Hu H., Tang J. H. Solution of a Duffing-harmonic oscillator by the method of harmonic balance. Journal of Sound and Vibration, Vol. 294, Issue 3, 2006, p. 637-639.
-
Al-Shyyab A., Kahraman A. Non-linear dynamic analysis of a multi-mesh gear train using multi-term harmonic balance method: sub-harmonic motions. Journal of Sound and Vibration, Vol. 279, Issue 1, 2005, p. 417-451.
-
Ghadimi M., Kaliji H. D. Application of the harmonic balance method on nonlinear equations. World Applied Sciences Journal, Vol. 22, Issue 4, 2013, p. 532-537.
-
Abbasbandy S. A numerical solution of Blasius equation by Adomian’s decomposition method and comparison with homotopy perturbation method. Chaos, Solitons and Fractals, Vol. 31, Issue 1, 2007, p. 257-260.
-
Rèpaci A. Nonlinear dynamical systems: on the accuracy of Adomian’s decomposition method. Applied Mathematics Letters, Vol. 3, Issue 4, 1990, p. 35-39.
-
Jiao Y. C., Yamamoto Y., Dang C., et al. An after treatment technique for improving the accuracy of Adomian’s decomposition method. Computers and Mathematics with Applications, Vol. 43, Issue 6, 2002, p. 783-798.
-
Shou Da-hua, He Ji-huan Application of parameter-expanding method to strongly nonlinear oscillators. International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 8, Issue 1, 2007, p. 121-124.
-
Sedighi H. M., Shirazi K. H. Vibrations of micro-beams actuated by an electric field via parameter expansion method. Acta Astronautica, Vol. 85, 2013, p. 19-24.
-
Molaei H., Kheybari S. A Numerical solution of classical van der Pol-Duffing oscillator by He’s parameter-expansion method. International Journal of Contemporary Mathematical Sciences, Vol. 8, Issue 15, 2013, p. 709-714.
-
Kaliji H. D., Ghadimi M., Barari A. Analytical solutions to non-linear mechanical oscillation problems. Journal of Vibroengineering, Vol. 13, Issue 2, 2011, p. 133-143.
-
He Ji-huan Max-min approach to nonlinear oscillators. International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 9, Issue 2, 2008, p. 207-210.
-
Ganji S. S., Ganji D. D., Davodi A. G., et al. Analytical solution to nonlinear oscillation system of the motion of a rigid rod rocking back using max-min approach. Applied Mathematical Modelling, Vol. 34, Issue 9, 2010, p. 2676-2684.
-
Zeng D. Q., Lee Y. Y. Analysis of strongly nonlinear oscillator using the max-min approach. International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 10, Issue 10, 2009, p. 1361-1368.
-
Zeng De-qiang Nonlinear oscillator with discontinuity by the max-min approach. Chaos, Solitons and Fractals, Vol. 42, Issue 5, 2009, p. 2885-2889.
-
Xiang Hong, Tang Bo-sen Application of L-P perturbation method in dropping shock problem. Journal of Vibration and Shock, Vol. 21, Issue 1, 2002, p. 39-42.
-
Chen An-jun Application of variational iteration method with energy method for nonlinear equation arisen from packaging system. Mathematical Problems in Engineering, 2013.
-
He Ji-huan He Chengtian’s inequality and its applications. Applied Mathematics and Computation, Vol. 151, Issue 3, 2004, p. 887.
-
He Ji-huan, Tang Jie Rebuild of King Fang 40 BC musical scales by He’s inequality. Applied Mathematics and Computation, Vol. 165, Issue 2, 2005, p. 909-914.
