Abstract
The explicit solutions for the natural frequencies and mode shapes of the orthotropic rectangular plate with four clamped edges are presented by the double finite cosine integral transform method. In the analysis procedure, the classical orthotropic rectangular thin plate is considered. Because only are the basic dynamic elasticity equations of the orthotropic thin plate adopted, it is not need prior to select the deformation function arbitrarily. Therefore, the solution developed by this paper is reasonable and theoretical. Finally, an illustrative example is given and the results are compared with those reported earlier. This method is found to be easier and effective. The results show reasonable agreement with other available results, but with a simpler and practical approach.
1. Introduction
The use of orthotropic plates is common in all the fields of structural engineering: civil, mechanical and aerospace. The wide use of such structures requires investigating the dynamic behavior of orthotropic plates in order to develop accurate and reliable design. From an engineering point of view, a complete solution to the problem of evaluating the modes and the dynamic response of an orthotropic plate can be given by the Finite Element Method when the material properties and the boundary conditions are known. However, in the preliminary design stage, when the dimensions and the properties of the materials must be selected, as well as in applying quality controls to the accuracy of the design by means of finite element calculations, it is very useful to have an analytical method to compute all the modal frequencies of orthotropic rectangular plates. The related publications can be counted in thousands [1]. In addition, a literature survey reveals that most previous investigations have mostly dealt with a scheme or technique that is only suitable for a particular type of boundary conditions. Due to the mathematical complexity of the situation, it is well known that the analytical solutions are generally available only for plates that are simply supported along at least one pair of opposite edges. Leissa gave a survey of research on rectangular plate problems up to 1970 [2-3]. The a further overview up to the beginning of this century is presented in Refs [4-5]. One of the most commonly used methods in free vibration analysis of plates is the Rayleigh-Ritz energy technique, where appropriate functions associated with various boundary conditions are chosen to describe the lateral deflection of the deformed plates. The chosen functions almost always do not satisfy the governing differential equation. Gorman used the superposition technique to solve approximately free vibration problems of plates for various geometries and boundary conditions [6, 7]. A set of static beam functions was used to determine the natural frequencies of elastically restrained plates [8, 9]. S. Hurlebaus et al. [10] have extended the Fourier series solution to other, more complicated, boundary conditions than the simply supported. The other numerical approaches, such as finite element method [13] and boundary element method [14] were usually adopted by many researchers to analyze the plate on elastic foundation.
Integral transform is one of the best approaches to obtain the explicit solutions of some partial differential equations used in elasticity [11]. This method has been often utilized to analyze some structural engineering problems [12]. Unfortunately, based on the author’s knowledge there are no reports about using finite integral transform to analyze the rectangular orthotropic plate with four clamped edges. In the paper the double finite cosine integral transform method is adopted to acquire the theoretical solutions of eigenfrequncies and vibration modes for the rectangular orthotropic thin plate with four clamped edges. In the analysis procedure, it is only to use the basic dynamic elasticity equations of the thin orthotropic and it is not need prior to select the deformation function arbitrarily. Therefore, the solution developed by present paper is reasonable and theoretical. In order to proof the correction of formulations, the numerical results are also presented to comparing with that of the other references.
2. Vibration of orthotropic thin plate and integral transform
According to the theory the classical orthotropic thin plate, the governing equation of motion for an unloaded plate is:
where and are the flexural rigidity of plate. In which and are Young’s moduli in the and directions respectively. is the shear modulus. Also and are Poisson’s ratios in the and directions respectively. and are the thickness and the density of plate. is the out-of-plane displacement. Assuming a harmonic vibration, one way write:
where is the shape function describing the modes of the vibration and is the natural circular frequency of the plate. Substitution of Eq. (2) into Eq. (1) gives:
where .
In order to solve the partial differential Eq. (3), the double finite cosine integral transform approach [11] is exploited.
If is a function of the two independent variables and , defined on the square , , the definition of double finite cosine integral transform is presented by the equation:
The inversion formula can be derived as :
where and and are the length and the width of the plate respectively.
The double integral transform of the first partial derivative term appeared in Eq. (3) may readily be written as:
and the third tern can be written as:
The second term is split into two parts. The first part considers the partial derivative with respect to first:
while the second part considers the partial derivative with respect to first:
Substitution of Eqs. (6)-(9) into Eq. (3) leads to:
The boundary conditions of a free plate are [15]:
Substituting the boundary conditions that described by Eq. (11) and Eq. (14) into Eq. (10), one can obtain:
Because the right of the Eq. (15) is definite integral, it is the constant. Let:
Therefore, Eq. (15) can be written as:
Substitution of Eq. (16) into Eq. (5) gives:
where:
It is clear that the Eq. (17) can meet the boundary conditions described by Eqs. (12) and (14). From the remaining boundary conditions presented by Eqs. (11) and (13), one can obtain:
Eq. (18) adding to Eq. (19) makes:
Similar, Eq. (23) adding to Eq. (21) makes:
where , .
Each coefficient of the and has to be vanish. What follows is a system of homogeneous algebraic equations:
Non-trivial solution of Eq. (24) requires the coefficient matrix to vanish. From this determinant the eigenfrequencies of the plate are calculated. The associated vibration modes are given by Eq. (17) after inserting the eigenfrequencies.
3. Numerical results
The previously derived expressions are applied to a rectangular thin plate on the foundation with four clamped edges. The geometrical and material properties are given as 4.0 m, 0.15, 0.12, 3.0×104 MPa, 2.0×104 MPa, 1.5×104 MPa, 0.2 m, 1750 kg/m3.
Table 1The nature frequencies of a plate
Frequencies | Order | ||||
1 | 2 | 3 | 4 | 5 | |
Superposition [7] | 5.855 | 6.345 | 6.548 | 6.598 | 6.614 |
Present paper | 5.855 | 6.344 | 6.549 | 6.599 | 6.615 |
In order to make the comparison with other method, the eigenfrequencies and the vibration modes are computed by the superposition method [7] and by the present approach. The calculation results are shown in Table 1. It is obvious that the results by two difference methods are excellent agreements. That also explains the present approach is correct. Fig. 1 to Fig. 4 illuminate the corresponding vibration modes respectively.
Fig. 1The 11 order vibration mode
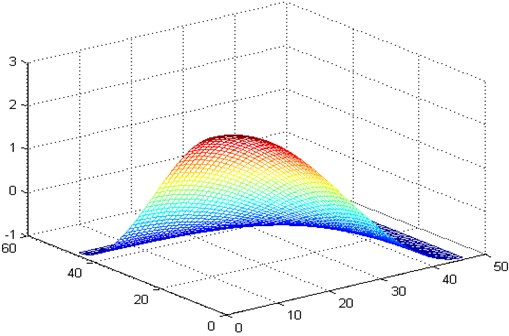
Fig. 2The 12 order vibration mode
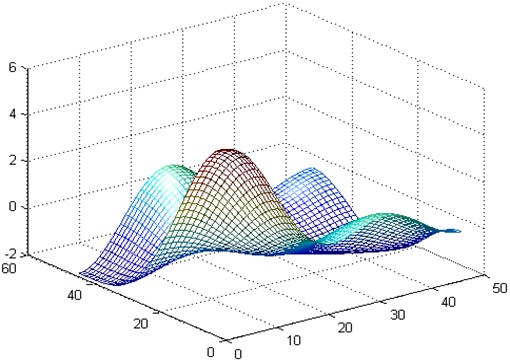
Fig. 3The 22 order vibration mode
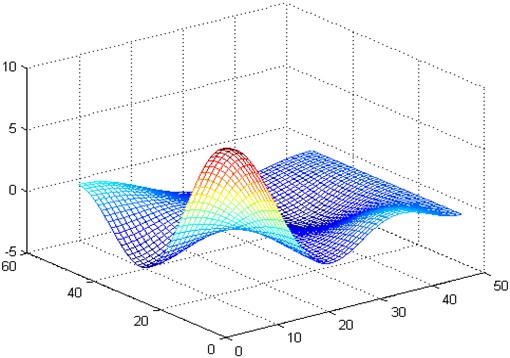
Fig. 4The 44 order vibration mode
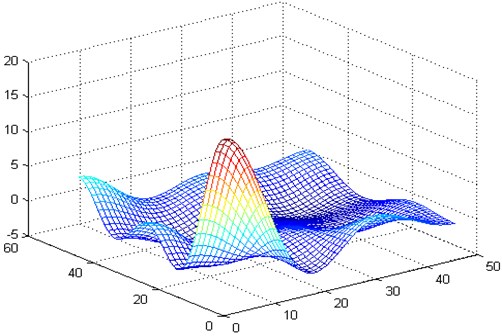
4. Conclusions
The present paper shows that the eigenfrequencies and the vibration modes of a classical orthotropic rectangular thin plate with four clamped edges can be calculated by integral transform method. The approach is based on the double finite cosine integral transform for the classical thin plate equation. One of the advantages of the method is that the results converge quickly and can be calculated with desired accuracy. The other is that after finishing the analytical derivation for the frequency determinant the calculation of eigenfrequencies and the vibration modes for given material data and geometry becomes straightforward. The present approach of analysis provides an efficient procedure for accurate results which should be of academic and practical importance.
References
-
Leissa A. W. Vibration of Plates. Acoustical Society of America, Massachusetts, USA, 1993.
-
Warburton G. B. The vibrations of rectangular plates. Proceeding of the Institute of Mechanical Engineers, Series A, Vol. 168, 1954, p. 371-384.
-
Leissa A. W. The free vibrations of rectangular plates. Journal of Sound and Vibration, Vol. 31, 1973, p. 257-293.
-
Warburton G. B. Response using the Rayleigh-Ritz method. Journal of Earthquake Engineering and Structural Dynamics, Vol. 7, 1979, p. 327-334.
-
Warburton G. B., Edney S. L. Vibrations of rectangular plates with elastically restrained edges. Journal of Sound and Vibration, Vol. 95, 1984, p. 537-552.
-
Gorman D. J. A comprehensive study of the free vibration of rectangular plates resting on symmetrically distributed uniform elastic edge supports. Journal of Applied Mechanics, Vol. 56, 1980, p. 893-899.
-
Gorman D. J. Free Vibration Analysis of Rectangular Plates. Elsevier North Holland, Inc., 1982.
-
Bapat A. V. Simulation of classical edge conditions by finite elastic restraints in the vibration analysis of plates. Journal of Sound and Vibration, Vol. 120, 1988, p. 127-140.
-
Zhou D. Natural frequencies of rectangular plates using a set of static beam functions in the Rayleigh-Ritz method. Journal of Sound and Vibration, Vol. 189, 1996, p. 81-88.
-
Hurlebaus S. An exact series solution for calculating the natural frequencies of orthotropic plates with completely free boundary. Journal of Sound and Vibration, Vol. 244, 2001, p. 747-759.
-
Sneddon Ian. H. The Use of Integral Transforms. McGraw-Hill, Inc., London, England, 1972.
-
Sneddon Ian. H. The Application of Integral Transform in Elasticity. McGraw-Hill, Inc., London, England, 1981.
-
Yang T. Y. A finite element analysis of plate on two parameters foundation model. Computer and Structure, Vol. 2, 1972, p. 573-616.
-
Zafrang A. E. A new fundamental solution for boundary element analysis of thick plate on Winkler foundation. International Journal Numerical Engineering, Vol. 38, 1995, p. 887-903.
