Abstract
Face gear dynamics is one of important studies of face gear drives. However, differences of dynamic behaviors of face gear drives between time varying and average mesh stiffness are not to be discussed. Thus, in this study, a mesh stiffness calculation solution of face gear drives is constructed, which is based on the proposed equivalent face gear teeth, and a four DOF dynamic model of face gear drives is formulated. Furthermore, differences of dynamic behaviors of face gear drives between time varying and average mesh stiffness are investigated. The result indicates instantaneous impacts are existed at start engagement points of face gear drives.
1. Introduction
Face gear drives, due to insensitive manufacture and alignment errors versus spiral bevel gear drives [1-5], are addressed by many scholars, and some research achievements of face gear dynamics are obtained by scholars [6-11]. However, according to the limited published issues, differences between the impact of time varying mesh stiffness on dynamic mesh forces of face gear drives and that of average mesh stiffness on dynamic mesh forces are not to be discussed. Thus, in this study, a mesh stiffness calculation solution of face gear drives, based on the proposed equivalent face gear teeth, is constructed, and a four DOF dynamic model of face gear drives is established. The differences of dynamic behaviors of face gear drives between time varying and average mesh stiffness are investigated. The result indicates an instantaneous impact is existed at start engagement points of face gear drives.
2. Constructed mesh stiffness calculation solution and four DOF dynamic model
2.1. Constructed mesh stiffness calculation solution
A face gear tooth is a kind of gear tooth associated with variable tooth thicknesses, and tooth pointing is produced at extreme outer radii of face gears, and undercut is observed at extreme inner radii of face gears. Thus, a face gear tooth can be assumed as a sequence in which modification involute gears are superimposed along its face width according to geometric characteristics of face gear teeth. Meanwhile, In order to avoid offset load phenomenon of face gear drives, tooth numbers of a pinion, which meshes with a face gear, are always less one to three teeth than a generation gear, which is employed to generate face gears. Therefore, according to the above assumption proposed and the working characteristics, face gear drives can be equivalent to involute modification gear drives based on mesh viewpoints, and an evolutionary procession of equivalent face gear teeth can be expressed as shown in Fig. 1.
As given in Fig. 1, according to the proposed equivalent face gear drives, a mesh stiffness calculation solution of face gear drives can be constructed by traditional Ishikawa model [12, 13].
2.2. Four DOF dynamic model
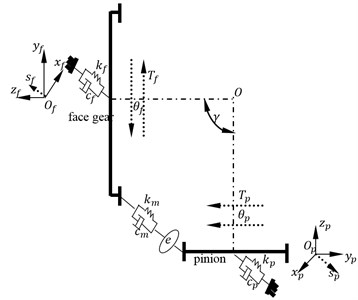
A four DOF dynamic model of face gear drives, as given in Fig. 2, is established for evaluating differences of face gear dynamic behaviors between time varying and average mesh stiffness.
Fig. 1An evolution diagram of equivalent face gear teeth
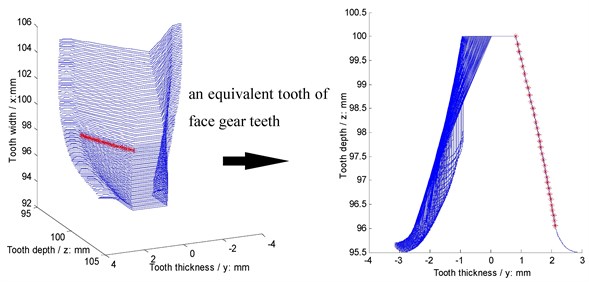
Fig. 2A four-DOF dynamic model of face gear drives
As shown in Fig. 2, mathematic equations of the dynamic model can be derived by:
where can be expressed as:
where is a torsion degree of freedom, is a bending degree of freedom, is a torsion, is a bending stiffness, is a bending damping, is a quality, is a moment of inertia, () is first derivative, () is second derivative, subscript and express a face gear and a pinion respectively. In addition, is mesh stiffness, is mesh damping, and is a comprehensive meshing error.
3. Simulations
In order to assess differences between the impact of time varying mesh stiffness on dynamic mesh forces and that of average mesh stiffness on dynamic mesh forces, geometric parameters, operating conditions and material characteristics of an example case of face gear drives are given in Table 1.
Table 1Parameters of an example case
Names | Values | Units | |
Geometric parameters | Modulus | 4 | mm |
Pressure angle | 20 | ° | |
Tooth number of pinions | 21 | – | |
Drive ratio | 2 | – | |
Shaft angle | 90 | ° | |
Tooth number difference between pinions and generation gears | 1 | – | |
Addendum coefficient | 1 | – | |
Clearance coefficient | 0.25 | – | |
Operating conditions | Power | 50 | kW |
Input rotation speed | 3000 | r/min | |
Material characteristics | Modulus of elasticity | 210000 | MPa |
Poisson ratio | 0.3 | – |
According to the proposed mesh stiffness calculation solution, and the parameters listed in Table 1, the time varying mesh stiffness and average mesh stiffness of the example case are simulated, as shown in Fig. 3. Moreover, the differences of dynamic mesh forces of face gear drives of the example case between time varying and average mesh stiffness, as shown in Fig. 4, are discussed.
Fig. 3Mesh stiffness simulated
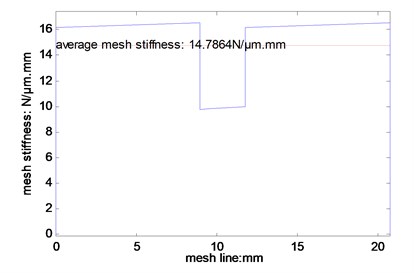
Fig. 4A diagram of the simulated differences
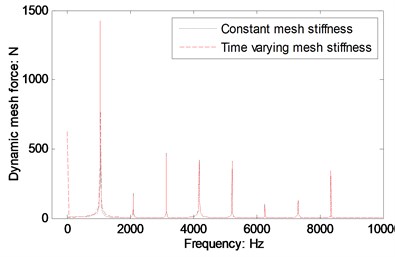
In the case of Fig. 4, a zero frequency incentive of dynamic mesh forces, which is the most important difference of dynamic behaviors between time varying and average mesh stiffness, is obtained. The result indicates a transitory shock at start engagement points of face gear drives is existed. Except the above phenomenon, the other differences almost can be neglected according to the simulation.
4. Conclusions
In this study, two important works can be extracted as follows:
1) A mesh stiffness calculation solution of face gear drives is constructed, which is based on the proposed equivalent face gear teeth.
2) Differences of dynamic behaviors of face gear drives between time varying and average mesh stiffness are obtained, and the result indicates an instantaneous impact is existed at start engagement points of face gear drives.
These contributions would be helpful to improve engineering applications of face gear drives.
References
-
Litvin F. L., Egelja A., Tan J., Chen D., Heath G. Handbook on Face Gear Drives with a Spur Involute Pinion. DTIC Document, 2000.
-
Litvin F. L., Fuentes A., Zanzi C., Pontiggia M. Design, generation, and stress analysis of two versions of geometry of face-gear drives. Mechanism and Machine Theory, Vol. 37, Issue 10, 2002, p. 1179-1211.
-
Litvin F. L., Gonzalez-Perez I., Fuentes A., Vecchiato D., Hansen B. D., Binney D. Design, generation and stress analysis of face-gear drive with helical pinion. Computer Methods in Applied Mechanics and Engineering, Vol. 194, Issue 36, 2005, p. 3870-3901.
-
Barone S., Borgianni L., Forte P. Evaluation of the effect of misalignment and profile modification in face gear drive by a finite element meshing simulation. Journal of Mechanical Design, Vol. 126, Issue 5, 2004, p. 916-924.
-
Litvin F., Bossler R., Chen Y.-J., Lewicki D., Heath G., Wang J.-C. Application of face-gear drives in helicopter transmissions. Journal of Mechanical Design, Vol. 116, Issue 3, 1994, p. 672-676.
-
Xiaozhen L., Rupeng Z., Zhengminqing L., Guanghu J. Analysis of coupled vibration of face gear drive with non-orthogonal intersection. Journal of Central South University (Science and Technology), Vol. 44, Issue 6, 2013, p. 2274-2279, (in Chinese).
-
Xiaozhen Li, Rupeng Zhu, Zhengminqing Li, Guanghu Jin Influences of frictional coefficent on vibration characteristc of face gear transimission system. Journal of Vibration Engnieering, Vol. 27, Issue 4, 2014, p. 584-588, (in Chinese).
-
Yang Z., Wang S.-M., Fan Y.-S., Liu H.-X. Bifurcation charactristics of face-gear transmission system. Journal of Harbin Institute of Technology, Vol. 3, Issue 43, 2011, p. 107-110, (in Chinese).
-
Yang Z., Wang S.-M., Fan Y.-S., Liu H.-X. Vibration characteristics of face-gear transmission system with parametric excitation. Journal of Chongqing University, Vol. 35, Issue 1, 2011, p. 26-35.
-
Hu Z. H., Tang J. Y., Chen S. Y., Lei D. C. Effect of mesh stiffness on the dynamic response of face gear transmission system. Journal of Mechanical Design, Vol. 135, Issue 7, 2013, p. 071005.
-
Wang R., Zhao N., Tao L., Jia Q., Guo H. Floating shaft load sharing method for face gear split torque transmission system. Research Journal of Applied Sciences, Engineering and Technology, Vol. 5, Issue 12, 2013, p. 3386-3392.
-
Shi J. L., Ma X. G., Xu C. L., Zang S. J. Meshing stiffness analysis of gear using the Ishikawa method. Applied Mechanics and Materials, Vol. 401, 2013, p. 203-206.
-
Zhu X., E Z. Analysis of Load Capacity of Gears. Higher Education Press, Beijing, 1992, (in Chinese).
About this article
The authors are grateful for the financial support provided by the National Natural Science Foundation of China under No. 51105194 and No. 51375226, and the Fundamental Research Funds for the Central Universities under No. NS2015049.
The authors declare that there is no conflict of interests regarding the publication of this article.
