Abstract
An optimal cuckoo search wavelet-based linear quadratic controller (ACSWBC) was introduced for seismic control of benchmark 76-story building with an active tuned mass damper (ATMD). A novel meta-heuristic cuckoo search (CS) algorithm was used to find the optimum gain matrix time to eliminate the trial and error. Furthermore, wavelet time-frequency analysis of excitation was used to adaptively design the controller by updating the weighting matrices to be applied to the control force of ATMD. The main advantage of the suggested control algorithm was adaptively calculating the optimum values of gain matrix components using the weights resolved on the response characteristics of the structure online. Furthermore, the robustness of the structural system was investigated to uncertainties in the stiffness matrix in the form of geometrical nonlinearities and multiplicative inclination. Results demonstrated that ACSWBC has preferable performance in attenuating the responses of structural system under several far and near fault seismic excitations.
1. Introduction
Intensive uncertain environmental phenomena such as high intensity winds, ocean waves and vigorous seismic ground motions may cause undesirable damages, during the tall buildings lifetime. To enhance safety and serviceability of structures, the theory of active structural control has been quickly expanded [1-3]. Between several passive and active control schemes considered, the tuned mass damper (TMD) has been comprehensively researched and employed in practice [4]. Simplicity and low maintenance cost are the main advantages of TMD. However, the physical parameters of TMD such as mass, stiffness and damping are not simply adoptable after installation of the control system. To gain the optimal performance, ATMs are designed and tuned on a specific frequency and frequently on first structural mode. Therefore, performance of TMD is very sensitive to mistuning, and its optimal performance is confined to a specific frequency band. Moreover, input excitation must be known as a prior knowledge which is not apllicable for earthquake or wind loads to find the parameter optimal values of a TMD system. This problem may be more critical in high-rise buildings where higher modes may have significant contribution to the structural response [5]. To improve the efficiency of TMD, an active actuator was added to the control system. The structural responses were adjusted continuously by means of the action of a closed-loop control scheme through some external energy supply. Therefore, an active tuned mass damper (ATMD) can be effective over a much wider frequency bands [6]. The Kyobashi-seiwa building was the first full-scale implementation of active control technology [7]. Several studies have been performed to determine the optimal actuator force for the active vibration control in structural systems. Most of the studies have focused on the application of classical linear control theories such as pole placement method [8], linear quadratic regulator (LQR) feedback control algorithm, linear quadratic Gaussian (LQG) control algorithm [9] and so on. The linear quadratic regulator (LQR) is commonly appropriate for vibration control of civil engineering. One of the major deficiencies of the classical LQR is its incapability to precisely account for the earthquakes or wind excitations. Most control methods are based on the optimization technique to enhance the performance using less control energy under certain constraint. However, difficulty in solving the optimal control problem lies in numerically solving matrix equations backward in each time interval, which requires the excitation to be known and the structural system characteristics such as mass, stiffness and damping matrices remain constant during the building lifetime. Furthermore, this is not applicable commonly for a tall structural system subjected to unknown excitations, uncertainties in stiffness matrix such as ignoring the geometrical nonlinearities and so on.
In recent years, several studies have been accomplished to improve the performance of the classical LQR. The modified LQR controller was introduced based on updating weighting matrices from a database of earthquakes [10]. Furthermore, the effect of specific earthquakes has been accounted for optimal controller design in a few recent researches [11]. However, the formulation in these studies lacks universality, as it may not ensure optimal performance for other earthquakes and offline databases were still needed. This paper introduces a cuckoo search wavelet-based linear quadratic controller (ACSWBC) formulation for the optimal seismic motion control of tall buildings with considering geometrical nonlinearities and suppressing uncertainties in stiffness matrix. The assessment of energy and frequency content of excitation and implementation of time-frequency analysis results to LQR formulations is pursued to assign the optimal time-varying gain matrices by updating the weighting matrices online. Wavelet analysis has been extensively used for time frequency analysis of the input excitation in structural control problems [12-14]. Further researches have been performed to enhance the performance of the wavelet analysis application in optimal structural control problems [15-17]. However, none of these studies evaluate the frequency and energy content of excitations to implement in classic LQR controller to design an adaptive LQR controller for seismic motion control of tall buildings considering uncertainties in the stiffness matrix in the form of geometrical nonlinearities and multiplicative inclination. Geometrical nonlinearities were considered in the structural control problems only in few studies [18]. The ACSWBC uses the multi-resolution wavelet analysis to obtain the time-varying energy in different frequency bands. Based on the energy in the different frequency bands over each time interval, the weighting matrices were modified online by using a scalar multiplier and the controller gains were optimized over each time window during the excitation. The LQR weighting matrices were tuned by an optimum factor related to the magnitude of the excitation energy on specific frequencies, which resonant could be happened. Hence, ACSWBC indirectly considers the effect of the external excitation. Moreover, the optimal updated weighting matrices are not impressed by the uncertainties in the system.
Cuckoo search (CS) is a meta-heuristic optimization algorithm which is introduced based on inspiration from the obligate brood parasitism of some cuckoo species [19]. CS is inspired by some species of a bird family called cuckoo because of their special lifestyle and aggressive breeding strategy. CS has been demonstrated the particular efficiency to quickly converge in global optimization problems. CS has been utilized newly as a formidable optimization algorithm in engineering problems [20-21] but not in the field of structural control. Recent studies have proven that CS algorithm is reliable and quick tool for optimization, which is outperforming other evolutionary algorithms. The update of the gain matrix is accomplished in interval of every time window by using CS. Whereupon, the control effort has low-frequency switching requirements as compared to a classic LQR controller. Employment of discrete wavelet transform (DWT) utilizing the multi-resolution analysis (MRA) algorithm develops the suggested controller fast and minimizes the effects of time delay problems [15].
In this study, authors propose an optimal controller to find optimal control force of ATMD by utilizing CS algorithm, classic LQR controller, DWT and MRA with considering uncertainties in system specifications. The exploit of DWT as a time-frequency tool assists to acquire time-varying energy in different frequency bands of seismic excitation. By means of CS, the ACSWBC weighting matrices are updated online according to the energy in each frequency band over a time window. The efficiency of the suggested approach to a number of pulse-like near-fault ground motions in a benchmark 76-story building is investigated. A 76-story benchmark building was determined to investigate the response control of structural system [22]. The benchmark building is used in this study, is a 306-m tall office tower suggested for the city of Melbourne, Australia. Furthermore, robustness of the mentioned structural system to uncertainties in the stiffness matrix in the form of geometrical nonlinearities and multiplicative inclination is examined. The ability of ACSWBC to tolerate the above circumstances is compared with LQR controller comprehensively. Results demonstrate that ACSWBC has superior performance in mitigating structural system responses induced by various near field and far field seismic excitations. From authors’ point of view, ACSWBC is beneficial over classical feedback controllers for active or hybrid control of structures for following reasons. First, ACSWBC can endure the imprecision in the structural system specifications. Second, it necessitates less prior knowledge of the structural system to be controlled. Third, it could be utilized to handle non-linearity in control problems such as uncertainties and geometrical nonlinearities in structural systems. At the end, it mostly converges quickly and are applicative for online active control of tall or complex buildings.
2. State-space equations of motion and classical LQR formulation
A state-space formulation of a -DOF linear structural system with m, number of active tuned mass dampers (ATMD) exposed to a based acceleration and active control force of ATMDs are investigated. The following matrix equations can be formulated as follows:
where , and are acceleration, velocity and displacement -dimensional vectors. , and are the mass, damping and stiffness matrices of the structural system, respectively. is the control effort -dimensional vector. and are location matrices with ×1 and × dimensional vectors, respectively which is the length of ground seismic motion time history of acceleration. is a state vector of order 2:
The system matrix is of order ×, active control matrix is of the order ×, the excitation matrix is of the order × and the gain matrix in a closed-loop control is of order × and assumed to be constant during seismic excitation. The classical linear quadratic regulator (LQR) algorithm can determine the optimal active control forces for the linear structural system with purpose of minimizing the cost function. To formulate an optimal control problem, a suitable cost functional merging two components (i) the states to be controlled and (ii) the ATMD control force has to be assembled with weightings on the two parts. The cost function can be formulated as follows:
The and matrices are entitled the control energy and response weighting matrices, respectively. The weighting matrices and are chosen in classical LQR at the first step based on prior information acquired by seismic excitation and structural system specifications. The control force is given by Eq. (4) where the gain matrix is acquired from the algebraic Riccati equation Eq. (8). In the classic LQR controller, the closed-loop gain matrix is assigned offline and it is constant during the motion control of structural systems. The idea of using the predetermined gain matrix operates well when there is no necessity of updating the systems specification. In real time, to determine the optimum weighting matrices or changing the assignment of relative importance of the responses of structural system and the control effort, the assessment of energy and frequency content of excitation and implementation of this information to LQR controller during the strong motion should be investigated.
3. Wavelet analysis
Intensive uncertain environmental phenomena such as seismic ground motions, ocean waves and strong winds are non-stationary in frequency and magnitude. Hence, the time-frequency analysis of theses excitations should be performed to illustrate the local frequency content and frequency bandwidth of the signal. The multi-resolution wavelet analysis as a time frequency tool has been used to resolve the time-varying energy in different frequency bands locally in time. The continuous wavelet transform (CWT) of a excitation signal , is described by the following equation:
where and is the wavelet basic function and the complex conjugate of , respectively. The ‘’ is a translation parameter indicating the locality and the ‘’ is a scale or dilation parameter representing the frequency content of the wavelet. To assure the integral energy determined by wavelet is independent of the dilation ‘’, factor is used for each value of wavelet transform. The discrete wavelet transform (DWT) is an implementation of the wavelet transform using a discrete set of the wavelet scales and translations maintaining some specified rules. By means of dyadic scale, the scale parameter ‘’ and translation parameter ‘’ are expressed as follows:
where is the set of positive integers. Pseudo-frequencies of each scale are determined by Eq. (11) (MATLAB, 2008):
where “” is a scale, “” is the sampling period, is the frequency maximizing the Fourier amplitude of the wavelet modulus (center frequency in Hz), and is the pseudo-frequency corresponding to the scale “” in Hz. By exploiting a dyadic wavelet filter into a particular frequency band, the excitation is analyzed along the time axis. To decrease the vanishing moment effect on excitation analysis, the suitable level of decomposition for the structural system should be exerted. The seismic excitation signal is subdivided into two parts when passing through one set of dyadic wavelet filters. The low-pass filter is the original signal minus some details. Decomposing process is continued to reach the final level of decomposition. The excitation can be decomposed to wavelet approximations and wavelet details at various levels, by the following equation:
where indicates the wavelet detail and represents the wavelet approximation, respectively. DWT can used as a powerful tool for real-time control of structures, because it can identify the time of earthquake frequency changes efficiently. The frequency range of is indicated by following equation:
Frequency range of level:
where and are denoted as follows:
where is the time step of . In addition, a wavelet low-pass filter is utilized to remove higher frequency components of the external excitation that prevent the stabilization of coefficients. It could be effective because the response of most civil structures is not influenced by high-frequency contents of the external excitations by any considerable level (special cases can be very rigid structures) [13]. By means of multi-resolution wavelet analysis with discrete wavelet transform (DWT), the information of the response of structural system in different frequency and signal energy could be determined. In each time window, the frequency content of the seismic excitation implements into the active control algorithm to decide the optimal control effort. Furthermore, by using DWT in multi-resolution analysis, the processing time is decreased and time delay problems is minimized significantly [15].
4. Cuckoo search optimization algorithm (CS)
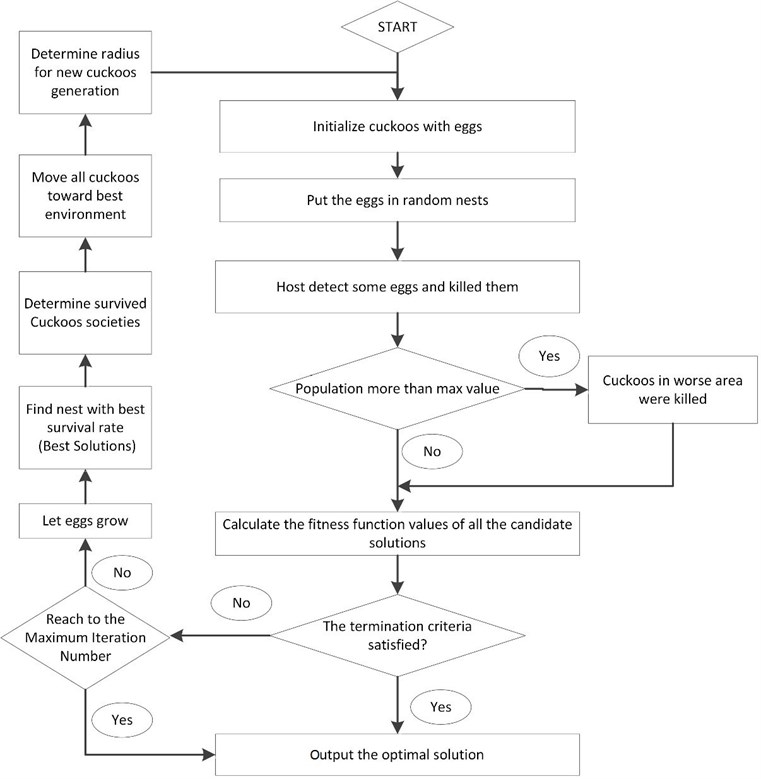
Yang and Deb developed a novel meta-heuristic optimization algorithm, which was named cuckoo search (CS) algorithm. CS is inspired by some species of a bird family called cuckoo because of their special lifestyle and aggressive breeding strategy. These birds set their eggs in the nests of other host with astonishing abilities to increase survival probability of their eggs. On the other side, some of host birds can distinguish the eggs of cuckoos and throw out the discovered eggs or build their new nests in new locations. Therefore, CS algorithm consists of a population of nests or eggs to simulate this strategy. The main simple rules of utilized CS are expressed as follows: (I) each cuckoo sets only one egg at a time and dumps it in a randomly chosen host nest; (II) the best nests with high quality of eggs are utilized in the next generations; and (III) the number of available host nests is constant and assumed before algorithm start; (IV) the probability of discovering of the guest egg which is laid by a cuckoo, is expressed by in the range of [0, 1]. This assumption can be estimated by the fraction pa of the n nests are replaced by new ones (with new random solutions). Each egg in a nest indicates a solution and a cuckoo egg indicates a new one. If the cuckoo egg is very familiar to the host eggs, the probability of discovering the cuckoo egg is reduced. The fitness function should be related to the quality or fitness of a solution which can simply be proportional to the objective function. The aim is to employ the new and potentially better solutions (cuckoos) to replace a not-so-good solution in the nests [19]. The structure of CS can be summarized as shown in Fig. 1.
Fig. 1The structure of CS algorithm
5. An optimal cuckoo search wavelet based linear quadratic controller (ACSWBC) formulation
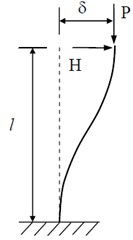
In a classic LQR feedback controller with the quadratic performance index that is represented in Eq. (8), the selection of the optimum components in penalty matrices and is crucial for the performance of structural system under seismic excitations. These weighing matrices express the importance to be assigned to structure responses to decide the control effort. Larger ‘’ components would impose major control efforts to attenuate the structural responses. Therefore, optimal gain matrix cannot be specified for the specific structure under various excitations. Furthermore, excitation such as earthquakes and hurricane could be non-stationary in frequency and energy content. In the presented ACSWBC, by using DWT and MRA the frequency and energy contents of excitation are computed. This data is sent to LQR controller to acquire weighting matrices during the strong motion. The capability of the wavelet to perform time-frequency analysis has been used to recognize the frequency contents of the excitation locally in time. Gain matrix can be updated during the strong seismic motion by means of MRA, which determines the frequency and energy contents of the seismic excitation in each time window. If the domain frequency of last time interval is adjacent to the natural frequency of the structural system, the resonance can be feasible. To mitigate the resonance probability in this time window, major control effort should be exerted without increasing the gain matrix components over all frequency bands. The ACSWBC adjusts the components of control energy weighting matrix in these bands whenever needed to optimally control the structural system. This adjustment can be accomplished by a factor that corresponds to magnitude of the local energy or system resonant probability. Moreover, the performance of classic LQR controller is crucially dependent on the precision of the mass and stiffness matrices. To enhance the privileges of the proposed ACSWBC, geometrical nonlinearity effects also considered. Geometrical nonlinearity significantly affects the structural behavior of a tall building structure under a vigorous earthquake excitation. Another advantage of the proposed ACSWBC is accounting for the uncertainties in the stiffness matrix in the form of geometrical nonlinearities and multiplicative inclination. Fig. 2 represents the P- geometrical nonlinearity of a column subjected to a horizontal load, and a vertical axial load, . The secondary bending moment induced by the horizontal displacement can be supposed to be generated by an additional horizontal load at the top of the column equal to , where is the height of the column element in each story. The equilibrium equation for the column in the horizontal direction can be described by the following equation:
where is the lateral stiffness of the column.
Fig. 2Geometrical nonlinearity effect on structural column
a)

b)
Eq. (16) is reproduced as follows:
where is the effective lateral stiffness of the column element in each story. Thus, the P- geometrical nonlinearity effect for tall buildings with rigid floors can modeled approximately by decreasing the lateral stiffness of the column based on Eq. (16). By utilizing effective lateral stiffness and regenerating the gain matrix in each time interval, any changes or uncertainties in structural system parameters are reflected on the updated gain matrix and more robustness can be implemented into the controlled tall building. To calculate the local energy distribution over the frequency band in the last second, the DWT controller is performed at each time window. The last one-second duration on the strong motion time history of acceleration under consideration is subdivided into 0.02-second time windows. The -th time window is . MRA computes the local energy content in the different frequency band over the last one-second time interval. The value of has been assumed to be less than one when the resonance occurs. This makes it possible to modify the weighting matrices for different frequency bands. The optimal control effort is computed for each window with an updated weighting matrix of the control force [] through the algebraic Ricatti equation, which leading to modified gain matrix. The updated weighting matrix and optimal control gain matrix are calculated for each 0.02-second time window, independent of the previous time-windows. Therefore, the computation of does not require to evaluate the transition conditions between the current and last time-windows. Total duration of the external excitation is divided into a number of time windows. For each window, ACSWBC modifies the weight matrices online to minimize the cost function by respecting the constraint in Eq. (1). The values of control energy weighting matrix components are decreased when the structural system has a crucially high value of response in the stories. So a high control force is generated, which is needed to mitigate the displacement responses of the structural system. Instead of assuming the fixed weighting matrix in traditional LQR controller, which creates its choices offline, the ACSWBC calculates the optimal values of the gain matrix, , adaptively by utilizing the time-varying values of the control energy weighting matrix, , relying on response specifications online. The main superiority of acquiring the optimal values of the control energy-weighting matrix [] in real time is that it has more ability to distinguish the proper gain matrix on special crucial frequencies in comparison with the traditional LQR controller which is a global optimal solution. To achieve the optimum response of the tall building with consuming a reasonable energy, the weighting matrices [] are computed by means of cuckoo search (CS) on the resonant band of frequency. To achieve this, the cost function integral is defined with the weighting matrices of ACSWBC in each time-window, and . The cost function is developed by the following formation:
In addition, the control effort formulation is described as follows:
where is the gain matrix of the th time-window. By solving the Ricatti equation, gain matrix is determined. The 2()×2() state weight matrix is described to be diagonal matrix with the following equation:
The diagonal matrix components and include the weights, which depend on the relative displacements and velocities, respectively:
The weighting matrix for the response states assumed to be constant for the tall building lifetime.
The control energy-weighting matrix is computed online for each time-window by a scalar multiplier and can be developed as:
where is a scalar parameter utilized to adjust the weighting matrix and is acquired based on the time-frequency analysis of a response state. Hence, the scalar parameter of a gain matrix can be stated as: 1 if the frequency of excitation is close to the natural frequency of system, 1 otherwise.
The values of the should be chosen between zero to one when the resonance probability increases. The optimal values of the are computed by means of CS algorithm to specify the optimum response of the structural system with expending a sensible amount of energy. The CS parameters are set in the first step. The dimension of search space is confined to be between [0, 1] for value. The random candidate value for is utilized to compute the control energy-weighting matrix [] of the -th window to accomplish the appropriate control of the structural responses. These parameters are number of nests (), step size parameter (), probability of discovering the eggs () and maximum number of iteration as the stopping criterion. The first locations of the nests are determined by the set of values assigned to each decision variable randomly is expressed by the following equation:
where determines the initial value of the th components of the th nest; and are the minimum and maximum allowable values for the th component; and rand is a random number in the interval [0, 1]. For next step, all of the nests except for the best location so far are replaced in order of quality by new cuckoo eggs produced with Lévy flights from their positions as:
where is the th component of ith nest in 1 iteration, a is the step size parameter, which is considered to be 0.1 in this paper, is the Lévy flights vector as in Mantegna’s algorithm, is a random number from a standard normal distribution between [0, 1] and is the position of best nest so far. The alien eggs discovery procedure is accomplished for all of the eggs except the best location by utilizing the probability matrix for each component of each solution. By considering the quality by fitness function, existing eggs are replaced by newly generated ones from their current position by random walks with step size such as [23]:
where is random number, is matrix which contains candidate solutions along with their parameters, and are different rows permutation functions applied on matrix. The generation of new cuckoos and the discovering of the alien eggs steps are performed alternately until a termination criterion is satisfied. The maximum number of frame analyses is considered as the algorithm’s termination criterion. The stopping criterion is assumed as a maximum number of iterations, which is limited to be 50 iterations. Finally the population size, , is specified to be 70. The selection of these values are based on trial and error to reach the most suitable convergence speed and required accuracy in the CS optimization algorithm. The fitness function for each time-window is expressed as follows:
where and are the controlled responses and control forces of structure computed by utilizing ACSWBC. Moreover, is the iteration index, and are the controlled responses and control forces of structural system computed by classic LQR. Furthermore, the TMD is turned off if the response of the structural system is less than the allowable displacement. Total duration of the seismic excitation is subdivided into 0.02-second time-windows. For each time-window, the fitness function is minimized by respecting the constraint in Eq. (1). The optimal control force is computed for each time-window with updated weighting matrix of the control effort [] by utilizing the algebraic Riccatti equation. Robust and low sensitivity LQR solver should be employed to prevent any instability in ACSWBC, according to utilizing the random values for by the CS algorithm. Fig. 3 shows the structure of suggested ACSWBC.
Fig. 3Flowchart of ACSWBC structure
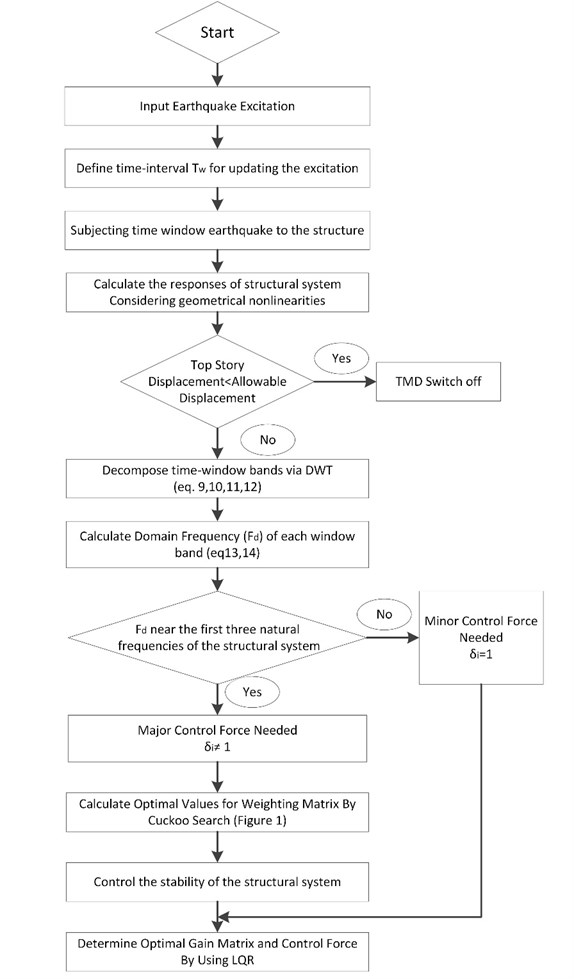
Suggested control effort stability and concluded gain matrix are observed in each time-window by calculating the and in the Eq. (25):
To attenuate the total energy demand, the ATMD is turned off until the displacements of structural system increases from the maximum allowable magnitudes that is determined to be one thousandth of the height of the each story level. The ACSWBC employed Daubechies wavelet and MRA to ensure that seismic excitation decomposition can be carried out fast and accurate. The Daubechies wavelets had wisely good localization in time and frequency to determine the effects of local frequency content in seismic excitation. In ACSWBC, Daubechies wavelet of order 4 (db4) was used. Therefore, the suggested ACSWBC relies on the online response characteristics, instead of a priori (offline) choice in contrast with the classical feedback controllers such as pole assignment method, LQR and so on. This modification allows the ACSWBC to compute the gain matrix online based of response feedback and the excitation frequency content.
6. An optimal cuckoo search wavelet based linear quadratic controller (ACSWBC) formulation
To illustrate the potential utilization of ACSWBC more preciously, the responses of dynamic time history analysis of a 76-story building with one ATMD under several far and near fault seismic excitations over the classical LQR were examined. In addition, the robustness of the structural system was compared in case of uncertainties in the form of multiplicative inclination and geometrical nonlinearities in the stiffness matrix. Both near-fault and far-fault seismic ground motions that have been identified to inflict extreme demands on structural systems, were employed. Near-fault seismic time history of accelerations were particularly chosen to represent the ACSWBC performance in relation to the characteristics of the excitation in both forward directivity and fling step cases. Moreover, a set of seismic ground motion records at the same site was chosen to investigate ACSWBC in case of far-field ground motion simultaneously. The basic specification of the seismic ground motion records is represented in Table 1. Fig. 4 exhibits ground motions for the far-fault and near-fault time histories of acceleration.
Table 1Specification of the seismic time history of acceleration
Type | Mechanism | Location | Station name | Distance (km) | PGA (g) | PGV (cm/s) | PGD (cm) |
Near field | Forward Directivity Pulse (FDP) | Imperia-Valley | H-E-ST0230 | 0.6 | 0.439 | 109.8 | 44.74 |
Northridge | SCS-ST052 | 6.2 | 0.612 | 117.4 | 52.47 | ||
Fling Step Pulse (FSP) | Chi-Chi | TCU-ST068NS | 3.01 | 0.462 | 292.2 | 867.7 | |
Chi-Chi | TCU-ST068EW | 3.01 | 0.565 | 176.7 | 324 | ||
Far field | Without Pulse (WP) | Northridge | WST-ST270 | 29 | 0.361 | 20.9 | 4.27 |
Northridge | CEN-ST155 | 30.9 | 0.465 | 19.3 | 3.48 |
The benchmark building of 76 stories, 306-m tall office tower suggested for the city of Melbourne, Australia is utilized to demonstrate the ACSWBC privileges. The total mass of the tall building is 153,000 ton, including heavy machinery in the plant rooms. The benchmark tall building is simulated like a vertical cantilever beam [22] as demonstrated in Fig. 5. The first five natural frequencies are 0.16, 0.765, 1.992, 3.790, and 6.395 Hz, respectively. The damping ratios of the first five modes are assumed to be 1 % of critical for the proportional damping matrix. On the top floor, ATMD is employed with an inertial mass of 2000 ton. By using CS algorithm, optimal mass value for tuned mass damper was computed between 1 % to 3 % of the total mass of the building. The ATMD damping ratio is set at 20 % of critical damping ratio and its natural frequency is tuned to be closed to the first natural frequency of the building.
Both the classic LQR controller and ACSWBC are utilized separately to control the ATMD on the benchmark building. The response of structure, control force and the total energy demand for both methods are compared. In addition, to illustrate the efficiency of the suggested ACSWBC, the case with one passive tuned mass damper (TMD), which is tuned to the first natural frequency of structure, is also compared. The last one second of the seismic ground motion record decomposes in each time-window. Based on the practical consideration in implementation of the updating, the time-window has been chosen, as well as (i) expected range of local frequency content which is dependent on the excitations and (ii) the possible range of the structural natural period [15] and eliminating the higher frequency components of the external seismic excitation [13]. The value of is updated by considering MRA, response feedback and excitation frequencies. The ACSWBC decided to turn off the ATMD until the displacement of the structures exceeds from the maximum allowable displacement. Otherwise, ACSWBC decide to implement control effort to mitigate the induced responses of structural system. The fifty number of solution candidates for values were created between zero and one. Each of candidate solution indicates value to compute the optimal LQR weighting matrices. By means of the structure defined in Fig. 1, the CS algorithm reiterates to determine the optimal LQR weighting matrix. ACSWBC modifies the weight matrices online to minimize the cost function by respecting the constraint in Eq. (1). Therefore, the optimal values of the updated weighting matrix of the control effort [] can be acquired adaptively based on frequency contents of the excitation in each time-window. The appropriate gain matrix can be obtained by using the CS algorithm in each time windows. All of computations have been carried out by MATLAB. In the case of CS and/or MRA failure and/or controller instability check, the controller weighting matrices do not modify in the mentioned time-window and assume to be equal to enhanced LQR updated weighting matrix, which is using geometrical nonlinearity. The application of discrete wavelet transform (DWT) which is utilizing the multi-resolution analysis (MRA) in LQR controller creates the suggested controller fast and omits the time delay related problems [15]. Suggested controller results demonstrate that the computational delay in comparison with updating time of time-windows is insignificant. The response of tall building, maximum ATMD control force and energy consumption of suggested controller were compared with classic LQR to verify the potential application of the ACSWBC.
Fig. 4Seismic ground motions for the far-fault and near-fault time histories of acceleration
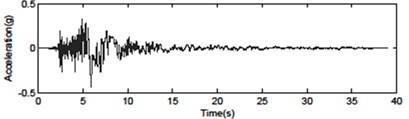
a) Imperial Valley H-E0230 – forward directive pulse (0.439 g)
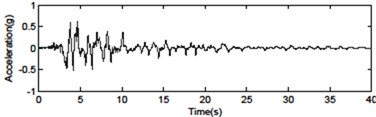
b) Northridge SCS052 – forward directive pulse (0.612 g)
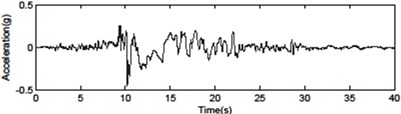
c) Chi-Chi TCU068NS – fling step pulse (0.462 g)
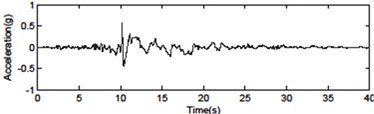
d) Chi-Chi TCU068EW – fling step pulse (0.565 g)
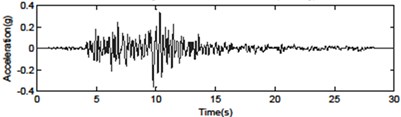
e) Northridge WST270 – without pulse (0.612 g)
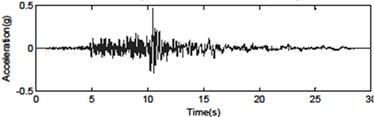
f) Northridge CEN155 – without pulse (0.465 g)
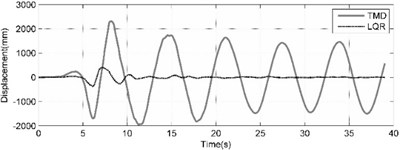
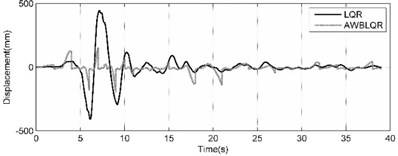
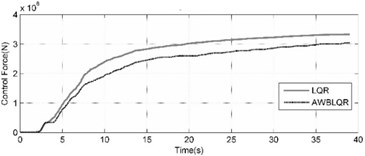
The top story displacement of benchmark building is comprehensively compared in the cases of uncontrolled (UN), TMD tuned to the first natural frequency, Classic LQR and ACSWBC under Imperia-Valley (H-EW-Station230) earthquake with considering the effects of geometrical nonlinearities in Fig. 6 and Table 2. Fig. 6(a) compares the TMD case and uncontrolled top story responses of benchmark building, Fig. 6(b) exhibits the TMD and LQR top story responses of benchmark building, Fig. 6(c) demonstrates the LQR and ACSWBC top story responses of benchmark building and Figure 5d illustrates the LQR and ACSWBC the cumulative control force under Imperia-Valley (H-EW-Station230) seismic excitation.
Fig. 5a) A Plan section, b) elevation view of 76 stories benchmark building
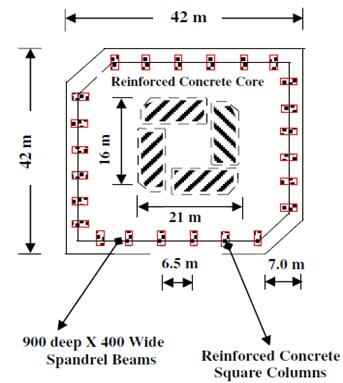
a)
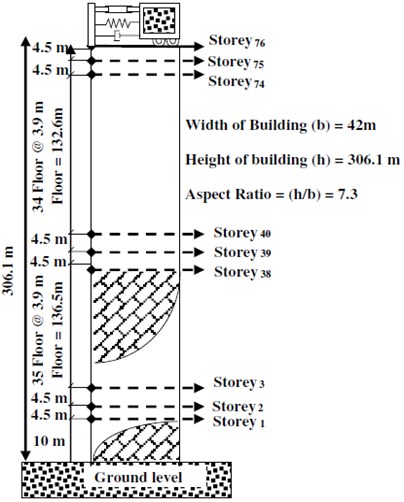
b)
Fig. 6Comparison of benchmark building responses under Imperia-Valley (H-EW-Station230) seismic excitation
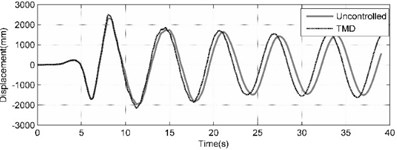
a) Top story displacement calculated by uncontrolled (UN) and controlled with TMD
b) Top story displacement calculated in cases of LQR and TMD controller
c) Top story displacement calculated in cases of ACSWBC and LQR
d) Cumulative control forces calculated in cases of LQR and ACSWBC
In Fig. 6 and the Table 2, it can be seen that the displacement reduction is not significant in passive TMD case. For Imperia-Valley, maximum displacement of the 76th floor of benchmark building is attenuated from 2492 mm in uncontrolled case to 2311, 405 and 198 mm in the cases of TMD, LQR and ACSWBC, respectively. In comparison with LQR, ACSWBC attenuates the 76th floor displacement about 51.1 % simultaneously the applied control force during the seismic excitation is even less than in LQR case. Furthermore, it can be concluded more reduction in structural member size of the benchmark building can be obtained during design procedure, which turns ACSWBC to a significantly efficient controller from an economic point of view. Moreover, to represent the efficiency of ACSWBC in reducing the response of the building more precisely, the 76-story benchmark building is subjected to five other earthquakes with different seismic mechanism. The effectiveness of ACSWBC is also illustrated for comparison in Table 3.
Table 2Effectiveness of controller systems in benchmark building for Imperia-Valley (H-EW-STATION230) seismic excitation
Building floor | Maximum uncontrolled response (mm) | Maximum controlled responses (mm) | Comparison of reduction percentages | |||
TMD | ATMD (LQR) | ATMD (ACSWBC) | ||||
1 | 2 | 3 | 4 | 5 | LQR vs. TMD | WPA vs. LQR |
[3]-[4]/[3] | [5]-[6]/[5] | |||||
10 | 77 | 75 | 59 | 38 | 21 | 35.6 |
20 | 234 | 226 | 160 | 100 | 29 | 37.5 |
30 | 464 | 438 | 262 | 171 | 40 | 34.7 |
40 | 750 | 711 | 339 | 236 | 52 | 30.4 |
50 | 1156 | 1092 | 353 | 273 | 68 | 22.7 |
60 | 1632 | 1535 | 341 | 268 | 78 | 21.4 |
70 | 2143 | 2007 | 378 | 209 | 81 | 44.7 |
76 | 2492 | 2311 | 405 | 198 | 82 | 51.1 |
Table 3Effectiveness of controller systems in benchmark building for seismic excitation for different seismic motions
Earthquake excitation | Maximum uncontrolled response (mm) | Max controlled response (mm) | Reduction percentages | |||
Mechanism | Name | Location | LQR | ACSWBC | ACSWBC vs. LQR | |
1 | 2 | 3 | 4 | [3]-[4]/[3] | ||
Near field | Imperia-Valley | H-EW STATION0230 | 2492 | 405 | 198 | 51 |
Northridge | SCS-STATION052 | 1594 | 629 | 512 | 19 | |
Chi-Chi | TCU-NS STATION068 | 8594 | 729 | 358 | 51 | |
Chi-Chi | TCU-EW STATION068 | 5700 | 698 | 298 | 57 | |
Far field | Northridge | WST STATION270 | 154 | 77 | 85 | –10 |
Northridge | CEN STATION155 | 181 | 73.7 | 64 | 13 | |
Almost the same behavior for the Imperia-Valley earthquake can be observed for these earthquakes. As demonstrated in Table 3, the suggested ACSWBC have potentially more influence on the seismic response mitigation in near field ground motions than far field ground motions. In all of the near field cases with considering the effect of geometrical nonlinearities, the obtained results from ACSWBC are superior from LQR. In addition, in far field ground motions with considering the effect of geometrical nonlinearities, the obtained results of ACSWBC are equal LQR, in the worst case. The time history of top story displacement and the exerted control force of benchmark building is widely compared in the cases LQR and ACSWBC under mentioned ground motions with considering the effects of geometrical nonlinearities in Figs. 7-9. From the Figs. 8-9, it can be seen that top story displacement peak as well as the cumulative control force of benchmark building are reduced by using ACSWBC in near field cases. The peak of exerted control force increases slightly just on the resonant band of frequency compared to the classic LQR, therefore, the response of structures decreases without higher penalty.
From the Fig. 8, it can be seen that top story displacement peak is slightly decreased in comparison with LQR case but the cumulative control force of benchmark building are reduced by using ACSWBC in far field cases.
Fig. 7Comparison of benchmark building responses due to Northridge (SCS-STATION052-FDP) seismic excitation
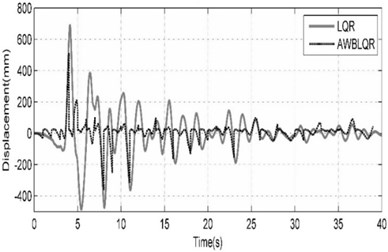
a) Top story displacement calculated in cases of ACSWBC and LQR
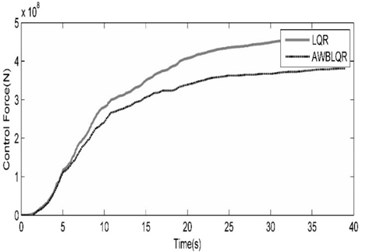
b) The cumulative control forces calculated in cases of LQR and ACSWBC
Fig. 8Comparison of benchmark building responses due to Chi-Chi (TCU-EW-STATION068-FSP) seismic excitation
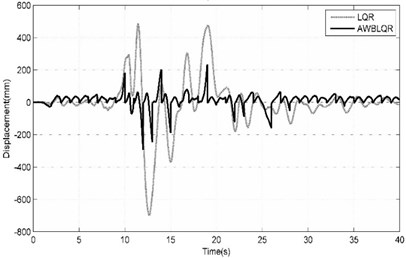
a) Top story displacement calculated in cases of ACSWBC and LQR
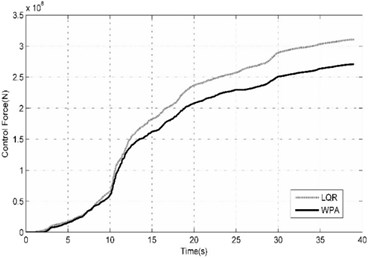
b) The cumulative control forces calculated in cases of LQR and ACSWBC
Fig. 9Comparison of benchmark building responses due to Northridge (CEN-STATION155- Far Field) seismic excitation
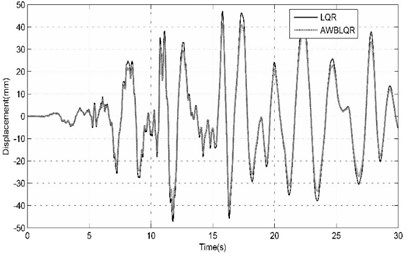
a) Top story displacement calculated in cases of ACSWBC and LQR
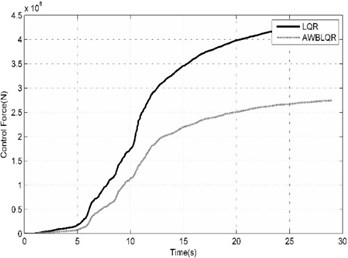
b) The cumulative control forces calculated in cases of LQR and ACSWBC
ACSWBC is more effective without the expense of requiring larger control forces and the reduction of structural responses is more significant in comparison with other controllers. Furthermore, in making the final judgment on the superiority of the ACSWBC, a set of time history analyses accomplished in this study in the presence of ±15 % stiffness uncertainty and geometrical nonlinearities effects. Results demonstrate that ACSWBC has satisfactory robustness to uncertainties. Comparisons between the displacement responses of the LQR and ACSWBC controlled structures to a set of excitations for +15 % and –15 % uncertainty in the stiffness are represented in Tables 4 and 5, respectively.
Table 4Top story maximum displacement, average maximum displacement of stories and total energy demand of the building for +15 % stiffness uncertainty in LQR and ACSWBC cases
Earthquake excitation | Top story maximum displacement (mm) | Average maximum displacement of stories (mm) | Total energy demand (N) | ||||||||
Mechanism | Name | Location | LQR | ACSWBC | ACSWBC vs. LQR | LQR | ACSWBC | ACSWBC vs. LQR | LQR | ACSWBC | ACSWBC vs. LQR |
1 | 2 | [1]-[2]/[1] | 3 | 4 | [3]-[4]/[3] | 5 | 6 | [5]-[6]/[5] | |||
Near field | Imperia-Valley | H-EW-STATION0230 | 405 | 198 | 51 % | 257 | 175 | 32 % | 3.320E+08 | 2.910E+08 | 12 % |
Northridge | SCS-STATION 052 | 680 | 510 | 25 % | 349 | 322 | 8 % | 4.650E+08 | 3.780E+08 | 19 % | |
Chi-Chi | TCU-NS STATION 068 | 659 | 341 | 48 % | 376 | 260 | 31 % | 3.400E+08 | 2.650E+08 | 22 % | |
Chi-Chi | TCU-EW STATION 068 | 698 | 292 | 58 % | 400 | 326 | 19 % | 3.110E+08 | 2.710E+08 | 13 % | |
Far field | Northridge | WST-STATION 270 | 75 | 84 | –12 % | 50 | 50 | 0 % | 3.750E+08 | 2.210E+08 | 41 % |
Northridge | CEN-STATION 155 | 78 | 62 | 21 % | 29 | 27 | 7 % | 3.620E+08 | 2.950E+08 | 19 % | |
Table 5Top story maximum displacement, average maximum displacement of stories and total energy demand of the building for –15 % stiffness uncertainty in LQR and ACSWBC cases
Earthquake excitation | Top story maximum displacement (mm) | Average maximum displacement of stories (mm) | Total energy demand (N) | ||||||||
Mechanism | Name | Location | LQR | ACSWBC | ACSWBC vs. LQR | LQR | ACSWBC | ACSWBC vs. LQR | LQR | ACSWBC | ACSWBC vs. LQR |
1 | 2 | [1]-[2]/[1] | 3 | 4 | [3]-[4]/[3] | 5 | 6 | [5]-[6]/[5] | |||
Near field | Imperia-Valley | H-EW-STATION0230 | 480 | 179 | 63 % | 300 | 194 | 35 % | 3.150E+08 | 2.620E+08 | 17 % |
Northridge | SCS-STATION 052 | 658 | 479 | 27 % | 377 | 343 | 9 % | 4.900E+08 | 3.500E+08 | 29 % | |
Chi-Chi | TCU-NS STATION 068 | 807 | 366 | 55 % | 473 | 287 | 39 % | 3.650E+08 | 2.900E+08 | 21 % | |
Chi-Chi | TCU-EW STATION 068 | 822 | 243 | 70 % | 471 | 356 | 24 % | 3.330E+08 | 2.920E+08 | 12 % | |
Far field | Northridge | WST-STATION 270 | 70 | 82 | –17 % | 50 | 51 | -2 % | 3.680E+08 | 1.930E+08 | 48 % |
Northridge | CEN-STATION 155 | 44 | 43 | 2 % | 24 | 22 | 8 % | 3.480E+08 | 2.700E+08 | 22 % | |
Table 4 compares the top story maximum displacement, average maximum displacement of stories and total energy demand of the building in two cases: LQR and ACSWBC controlled tall building with +15 % stiffness uncertainty and geometrical nonlinearity effects. Optimal control effort is obtained for each window with updated weighting matrix of the control effort by utilizing ACSWBC, the superior performance in attenuating the responses of benchmark building can be seen, even at the presence of perturbations in the stiffness matrix. The ACSWBC decreases the 76th story peak displacement, average maximum displacement of stories and total energy demand in near field seismic excitations by 46 %, 23 % and 17 % respectively, when compared to the LQR. Also as demonstrated in Table 4, the ACSWBC attenuates the peak displacement of 76th story, average maximum displacement of stories and total energy demand of controlled benchmark building in far field seismic excitations by 5 %, 3.5 % and 30 % respectively, when compared to the LQR in case of +15 % uncertainty in stiffness.
Table 5 compares the top story maximum displacement, average maximum displacement of stories and total energy demand of the building in two cases: LQR and ACSWBC controlled tall building with –15 % stiffness uncertainty and geometrical nonlinearity effects. The ACSWBC decreases the 76th story peak displacement, average maximum displacement of stories and total energy demand in near field seismic excitations by 54 %, 27 % and 19 % respectively, when compared to the LQR. Also as demonstrated in Table 5, the ACSWBC attenuates the peak displacement of 76th story, average maximum displacement of stories and total energy demand of controlled benchmark building in far field seismic excitations by –8 %, 3 % and 35 % respectively, when compared to the LQR in case of –15 % uncertainty in stiffness. Results demonstrate that in case of ±15 % stiffness uncertainty and geometrical nonlinearities effects the performance of ACSWBC in even better than LQR. Furthermore, since the structure is assumed to remain linear during seismic excitations, the structure will be stable and preserves robust stability in the presence of small perturbations by controlling Eq. (24) in each time interval. In general, results demonstrate that the ACSWBC have potentially more influence on the seismic response mitigation in near field ground motions than earthquakes having a far fault effect. In addition, the obtained vibration results from the presented method are superior from the LQR controller method, in all of the cases. In the case of earthquakes having a far fault effect, the suggested method in comparison with LQR method, resulted in slightly larger energy demand under far-fault ground motions compared to near-fault earthquakes. The control forces for the two systems are not very different for most of the times over the duration except from the peak control. Consequently, obtained results indicated that the ACSWBC is a promising procedure to structural control.
7. Conclusions
In this paper, we present an optimal CS based controller for seismic control of a tall buildings. By combining the magnificent effect of cuckoo search algorithm and the conventional LQR controller to updating the gain matrix during excitation. The ACSWBC is aimed at controlling of benchmark building based on decomposition of excitation and optimization problems. The weighting matrices of proposed ACSWBC are determined adaptively by utilizing the wavelet analysis of the response locally in time to account for the time-varying frequency distribution of the energy content representing the effect of the non-stationary seismic excitations. By considering the effect of the excitation on the fitness function, the optimal weighting matrices for each time window can be computed by using the CS algorithm in each time interval. ACSWBC minimizes the a priori requirement of predetermining on the weighting matrices usually carried out arbitrarily in the classical LQR controllers. In addition, the ACSWBC could predict geometrical nonlinearities and handle any change in stiffness of the structure based on the responses during excitation online. The capability of ACSWBC was investigated through the performance of controller on well-known benchmark 76 story problem through a set of ground motions. The results obtained by the modified CS algorithm are satisfying. Furthermore, the robustness of the ACSWBC to uncertainties in structural parameters is evaluated for geometrical nonlinearities effects and multiplicative perturbations in the stiffness of a tall building. The obtained results indicated that ACSWBC is a promising procedure to structural control. Considering all the results, the ACSWBC is observed to be more impressive than the LQR controller in attenuating the structural responses due to seismic excitations. Consequently, ACSWBC can be characterized as a powerful tool for optimal structural control in especially near field seismic excitation.
References
-
Wang P. C., Kozin F., Amini F. Vibration control of tall buildings. Engineering Structures, Vol. 5, Issue 4, 1983, p. 282-288.
-
Polycarpou M. M., Ioannou P. A. A robust adaptive nonlinear control design. Automatica, Vol. 32, Issue 3, 1996, p. 423-427.
-
Amini F., Karagah H. Optimal placement of semi active dampers by pole assignment method. Iranian Journal of Science and Technology, Transaction B: Engineering, Vol. 30, Issue 1, 2006.
-
Singh M. P., Singh S., Moreschi L. M. Tuned mass dampers for response control of torsional buildings. Earthquake Engineering & Structural Dynamics, Vol. 31, Issue 4, 2002, p. 749-769.
-
Soleymani M., Khodadadi M. Adaptive fuzzy controller for active tuned mass damper of a benchmark tall building subjected to seismic and wind loads. The Structural Design of Tall and Special Buildings, 2014.
-
Soong T. Active Structural Control: Theory and Practice. John Wiley & Sons, New York, 1990.
-
Yang J., Soong T. T. Recent advances in active control of civil engineering structures. Probabilistic Engineering Mechanics, Vol. 4, 1988, p. 179-188.
-
Kautsky J., Nichols N. K., Van Dooren P. Robust pole assignment in linear state feedback. International Journal of Control, Vol. 41, Issue 5, 1985, p. 1129-1155.
-
Athans M. The role and use of the stochastic linear quadratic gaussian problem in control system design. IEEE Transaction on Automatic Control, Vol. 16, Issue 6, 1971, p. 529-552.
-
Panariello G., Betti R., Longman R. Optimal structural control via training on ensemble of earthquakes. Journal of Engineering Mechanics, Vol. 123, Issue 11, 1997, p. 1170-1179.
-
Wu W.-H., Chase J. G., Smith H. A. Inclusion of forcing function effects in optimal structural control. Proceedings of the First World Conference on Structural Control, 1994.
-
Basu B., Gupta V. K. Seismic response of SDOF systems by wavelet modeling of nonstationary processes. Journal of Engineering Mechanics, Vol. 124, Issue 10, 1998, p. 1142-1150.
-
Adeli H., Kim H. Wavelet-hybrid feedback-least mean square algorithm for robust control of structures. Journal of Structural Engineering, Vol. 130, Issue 1, 2004, p. 128-137.
-
Amini F., Shahidzadeh M. S. Damage detection using a new regularization method with variable parameter. Archive of Applied Mechanics, Vol. 80, Issue 3, 2010, p. 255-269.
-
Basu B., Nagarajaiah S. A wavelet-based time-varying adaptive LQR algorithm for structural control. Engineering Structures, Vol. 30, Issue 9, 2008, p. 2470-2477.
-
Amini F., Hazaveh N. K., Rad A. A. Wavelet PSO-based LQR algorithm for optimal structural control using active tuned mass dampers. Computer-Aided Civil and Infrastructure Engineering, Vol. 28, Issue 7, 2013, p. 542-557.
-
Amini F., Samani M. Z. A wavelet-based adaptive pole assignment method for structural control. Computer-Aided Civil and Infrastructure Engineering, Vol. 29, Issue 6, 2014, p. 464-477.
-
Jiang X., Adeli H. Dynamic fuzzy wavelet neuroemulator for non-linear control of irregular building structures. International Journal for Numerical Methods in Engineering, Vol. 74, Issue 7, 2008, p. 1045-1066.
-
Xin-She Yang, Deb S. Cuckoo search via Levy flights. World Congress on Nature & Biologically Inspired Computing, Vol. 37, Issue 2, 2009, p. 106-111.
-
Gandomi A., Yang Xin-She, Alavi A. Cuckoo search algorithm: a metaheuristic approach to solve structural optimization problems. Engineering with Computers, Vol. 29, Issue 1, 2013, p. 17-35.
-
Kaveh A., Bakhshpoori T. Optimum design of steel frames using Cuckoo Search algorithm with Lévy flights. The Structural Design of Tall and Special Buildings, Vol. 22, 2013, p. 1023-1036.
-
Yang J., Agrawal A., Samali B., Wu J. Benchmark problem for response control of wind-excited tall buildings. Journal of Engineering Mechanics, Vol. 130, Issue 4, 2004, p. 437-446.
-
Tuba M., Subotic M., Stanarevic N. Modified Cuckoo search algorithm for unconstrained optimization problems. Proceedings of the 5th European Conference on European Computing Conference, 2011, p. 263-268.
About this article
The authors would like to thank the Editor and the anonymous reviewers for their constructive comments and valuable suggestions to enhance the quality of the article.
