Abstract
Structural strength, stiffness, etc. are essential safety performances of mine refuge chamber. In this article, the safety performance of the chamber which is under the impact load was evaluated by the method of numerical analysis. First of all, according to some relative standards, a chamber model was established by applying numerical modeling software. In this way, a method of finite element analysis (FEA) was instituted and we used AUTODUN to simulate the process of transmission of blast waves in the underworkings. On the basis of Fourier transform theory, the spectrum analysis of the blast waves acting on the chamber has been done. In order to obtain the natural frequency, a model analysis of the chamber was made by applying OPTISTRUCT. Then the main frequency and the natural frequency were compared. The result shows that the resonance will not happen so that the safety performance of the chamber meets the demand of engineering safety. The structural strength of the chamber was analyzed by using LS-DYNA, and the result comes out that the pressure throughout the chamber will not cause damage to the chamber. After that, according to the simulation results, we proposed some pieces of advice which will be meaningful for the design and the improvement of the chamber.
1. Introduction
1.1. Background
Mining plays a critical role in economic development and thus remains an important part of economic structure in many countries, such as the US, China, South Africa, etc. [1]. However, mine accidents frequently occur in the process of mining [2], and the shock waves from gas explosion or the explosion of gas mixture and coal dust are destructive, posing a major threat to the miners’ lives. According to the investigation of various countries in the world, in fire and explosion accidents, the number of the death which is caused directly by the fire and the explosion just takes a small percentage of the total death toll [3]. In fact, most of the deaths are caused by suffocation because of a gug delay and by poisoning because of not escaping from the toxic gas. In such cases, a refuge chamber installed in the mine will be of great significance to resist the shock waves, provide food, water and oxygen continuously for trapped miners for over 96 hours, and guide the outside rescue work via its telecom set and monitors [4]. Such countries with developed mining industries as the US, Australia, Canada, South Africa, etc., have attached great importance to mine refuge chamber, and have successful cases in rescuing the trapped workers using the refuge chamber. Therefore, the research of the refuge chamber can make a critical difference in the emergency rescue work of the trapped coal miners [5].
1.2. Past research efforts
When the explosion happens, the outside of the refuge chamber can be impacted by the tremendous shock waves within seconds. Therefore, the strength of the chamber must be tested to ensure that it can dissolve the shock waves. Besides, when any of the principal frequency components of the shock waves is equal or close to the natural frequency of the chamber, resonance occurs, which may weaken the anti-shock capacity of the chamber, or even damage it. Therefore, the natural frequency of the chamber must be considered in designing the chamber structure in order to avoid the occurrence of the resonance.
The researches on gas explosion applying the numerical modeling software have been done by Di Sarli et al. The result indicates that the flame propagation rate and the overpressure change gained by numerical model meets the experimental result [6]. Zhao Huanjuan, et al. made a numerical analysis on the safety performance of chamber under the circumstance that it is impacted by triangle waves. The article suggests that FEM modeling of the refuge chamber response under blast loading is verifiable and resultful [7]. However, the potential damage caused by resonance was ignored and only the blast waves with the triangle waves was imitated in past study, which maybe do not meet the actual situation. What’s more, it is rare at present to conduct a model analysis under the circumstance that the chamber is impacted by blast waves.
2. Establishment of finite element model
2.1. The structure of the refuge chamber
The refuge chamber model was established according to coal mine emergency management system construction Interim Provisions [8]. The coal mine mobile refuge chamber is made up of 10 cabins. The dimension of the refuge chamber is 11336 mm×1800 mm×2080 mm. The fore end wall has an entry door, and the rear end wall has an emergency escape hatch. The interior of the cabin has reinforcing ribs uniformly. The entry door and the fifth cabin are equipped with an observation window respectively. The skin of the refuge chamber is made up of 8mm-thick plate of steel. All cabins are connected by flanges.
2.2. Meshing
The model of the chamber was meshed by HYPERMESH. When the component size in one direction is much larger than the other two directions, the simulation was made in one-dimensional element. When the component size in two directions is much larger than another direction, the simulation was made in two-dimensional element. When the sizes in three directions of component are in the same order magnitude, it was meshed in three-dimensional grid [9]. On these bases, our result is that the joint flanges, reinforcing ribs, door panel and doorframe are meshed with three-dimensional grid, and the skin of cabin was meshed in two-dimensional element. The whole finite element model comprises 380822 elements and 578640 nodes. By using master-slave relationship rigid element RBE2, the welding was simulated, and 277636 pairs welding unites are formed. The finite element model of refuge chamber is shown in Fig. 1.
Fig. 1Finite element model of refuge chamber
2.3. Material property
In the analysis, the material of refuge chamber was chosen as Q345 steel, and material parameters were listed in Table 1.
Linear elastic fracture model was used in toughened glass of the observation window, and its material parameters were shown in Table 2.
Table 1Material parameters of the refuge chamber
The name of the parameter | Detail |
Yield strength | 345 MPa |
Ultimate strength | 470 MPa |
Density | 7800 kg/m3 |
Modulus of elasticity | 210 GPa |
Poisson’s ratio | 0.3 |
Table 2Material parameters of toughened glass
The name of the parameter | Detail |
Yield strength | 43 MPa |
Density | 2500 kg/m3 |
Modulus of elasticity | 73 GPa |
Poisson’s ratio | 0.28 |
2.4. Boundary conditions
The chamber model was fixed at the bottom on the ground through pressing plate and anchor bolts, etc., thus there is no relative movement. When the numeric calculation was being done, constraints in six directions would be set.
3. Numerical analysis
3.1. Spectrum analysis of explosion shock wave
According to Fourier transformation theory [10], any complicated signal can be decomposed into different frequencies of sine function and cosine function to some extent [11]. The shock wave from explosion is a complicated vibrant signal which changes with time, and Fourier transformation can help to decompose the shock waves into frequency components and identify the principal ones [12].
On the basis of AUTODYN, the process of explosion against the refuge chamber was simulated and the laneway was designed as a semicircle arch, an equal cross section straight laneway model with a height of 2.6 m and a width of 3.2 m, and the total length is 160 m according to the standard requirements. The length of the explosion source is 28 meters, and the distance from explosion shock wave to the front of the refuge chamber is 100 meters. The refuge chamber was placed in the horizontal geometric center of the laneway. The flow field pressure and pressure monitoring points were set in the geometric center of the laneway including one meter in fore end wall of the chamber, the rear end wall of refuge camber, two sides wall and the roof of each cabin. After simulating the explosion process in the laneway and the impact on the surface of the chamber, the authors obtained the explosion shock wave pressure history curves of each cabin, and the explosion shock wave pressure history graph of fore end wall is shown in Fig. 2.
Fig. 2 shows that the time of explosion shock wave transmitted to the fore end wall of the refuge chamber is 175 ms. Due to encounter with refuge chamber, pressure value rapidly rose to the first top 713.9 KPA, and rapidly decreased to the second top 640 KPa. The pressure reached maximum at 178 ms, and then the pressure value declined to 544 KPa rapidly. The minimum pressure is 99.423 KPA in the whole explosion process.
Based on MATLAB software, the biggest explosion shock wave history graph from fore end wall was taken to be used in the spectrum analysis. The length of sample time is 1s and sample interval is 1 ms. Amplitude spectrum is shown in Fig. 3.
Fig. 2Explosion shock wave pressure history curve of fore end wall
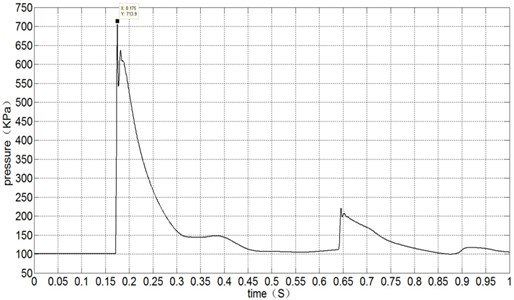
Fig. 3Amplitude spectrum
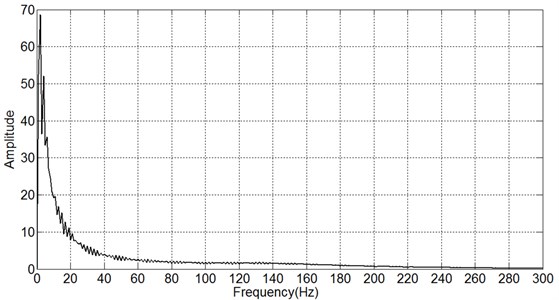
As is shown in Fig. 3 the frequency components of explosion shock wave have low frequencies. There are three high peaks in amplitude spectrum. The highest amplitude is at 2 Hz, and the value of the amplitude is 68.65, and the second one appeared at 4 Hz and the value of the amplitude is 52.14. The third appeared at 6 Hz and the value of the amplitude is 35.59. When the frequency reaches 35 Hz, the value of the amplitude declines to 3.569 rapidly. The amplitude is close to 0 when the frequency reaches 300 Hz.
3.2. Modal analysis
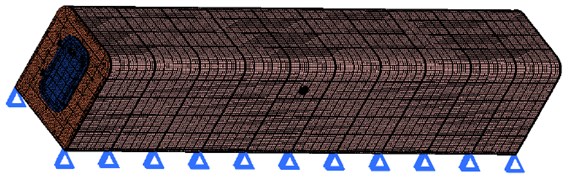
To prevent the main frequencies of explosion shock waves from falling into the range of natural frequencies which may lead to chamber resonance, it is necessary to make modal analysis of the chamber, which can help to reveal and assess the dynamic performance of the chamber and optimize the structure designing [13]. Low mode frequencies tend to couple with external conditions and that the effect of low mode shapes is more serious than high mode shapes in the dynamic analysis of structure. So the authors only focused on the first six mode frequencies of the chamber, and then made a dynamic analysis by applying OPTISTRUCT. The natural frequencies and the corresponding mode shapes of the chamber under 3 different constraint conditions were obtained. The diagrammatic drawings of 3 different constraint conditions are shown in Fig. 4.
Table 3 shows the natural frequencies and increase with the number of constrains and the stiffness of the chamber structure increases as well. By comparison, the natural frequencies of the chamber under the first constraint condition and the second constraint condition are significantly different while those frequencies under the second and the third constraint condition only change slightly.
Analysis based on mode shapes:
1st mode shape: the 3 constraint conditions are at the same mode shape, where the upper part of the chamber swings along the axis, either in the minus or plus direction.
2nd mode shape: the chamber swings along the axis either in the minus or plus direction under the first constraint condition, while the vibration of the sides and top of the chamber follows the pattern of 1st mode shape.
3rd mode shape: the upper and lower ends of the chamber twist in vibration under the first constraint condition while vibration of the sides and top of the chamber follows the pattern of 2nd mode shape.
4th mode shape: the vibration of the sides and top of the chamber follows the 1st mode shape while the vibration of the right door occurs along the axis either in the minus or plus direction under the second and the third constraint conditions, and the vibration of the other parts is not significant.
5th mode shape: the vibration of the sides and the top of the chamber follows the 1st mode shape under the first constraint condition while the front and rear of the chamber twist around the axis under the second and third constraint conditions.
6th mode shape: the front and rear doors of the chamber vibrate along axis either in the minus or plus direction under the 3 constraint conditions.
Fig. 4Three different constraint conditions

a) The first constraint condition
b) The second constraint condition

c) The third constraint condition
Table 3Former six natural frequencies of different constrain conditions
Modal order | Natural frequencies / Hz | ||
The first constraint | The second constraint | The third constraint | |
1 | 30.57 | 39.88 | 40.33 |
2 | 37.29 | 71.56 | 72.05 |
3 | 48.13 | 72.73 | 73.13 |
4 | 60.29 | 74.18 | 74.42 |
5 | 60.83 | 74.45 | 74.99 |
6 | 61.85 | 75.43 | 75.69 |
It is generally required that the natural frequencies stay as far as possible off the main frequencies of external excitation in structure designing [14]. In comparison, the natural frequencies under the second and the third constraint conditions are high and the mode shapes are reasonable, considering that the relative frequencies under the second and the third conditions are slightly different and the stiffness of the chamber structure does not vary much, and that the factors such as mobility of the chamber and installation technology must be involved and the second constraint condition be regarded as the best.
The scale factor was 5. The front six vibration modes under the second constraint condition were shown in Fig. 5.
Fig. 5Former six vibration modes of refuge chamber
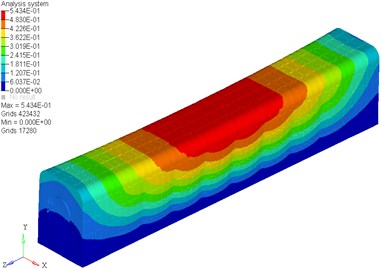
a) The first vibration mode
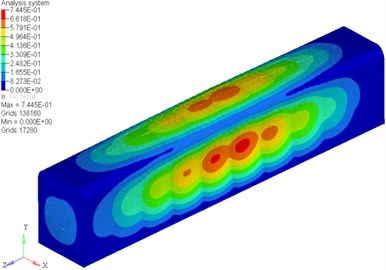
b) The second vibration mode
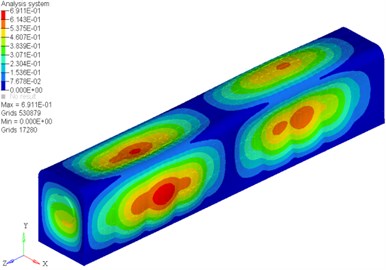
c) The third vibration mode
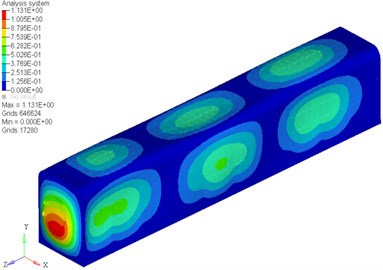
d) The fourth vibration mode
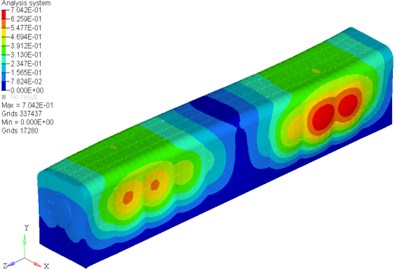
e) The fifth vibration mode
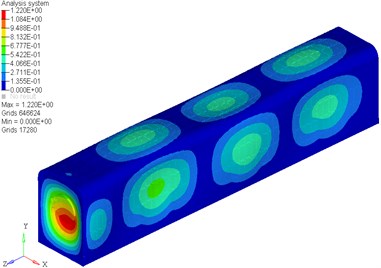
f) The sixth vibration mode
3.3. Comparing spectrum analysis with natural frequencies
In engineering, excitation frequencies and natural frequencies should have a least 10 % difference to avoid resonance [15]. From the results of modal analysis, it can be seen that the first 6th natural frequency of the refuge chamber is distributed in 39 Hz-76 Hz with the method of constraints on both ends of each cabin. As the main frequencies components of explosion shock wave are 2 Hz, 4 Hz and 6 Hz, which are much less than the first 6th natural frequencies, the resonance won’t produce. So under the impact of explosion shock wave, natural frequencies of the refuge chamber avoid the principal frequencies of explosion shock wave, and the modal design of the refuge chamber is reasonable.
3.4. Strength analysis
As the refuge chamber needs to resist explosive shock wave, it must have a sufficient performance of strength, stiffness and sealing. On the basis of dynamic optimization design, strength analysis is carried out [16]. The flow field pressure curves of explosion shock wave were loaded to appropriate location of the refuge chamber which is gotten from AUTODYN simulation results. By analyzing the displacement, stress and relative displacement of sealing position of the refuge chamber with LS-DYNA, maximum displacement contour and displacement history graph, maximum stress contour and stress history graph and maximum relative displacement history graph of sealing position were obtained [17].
Fig. 6Maximum displacement moment contour and displacement history graph of refuge chamber
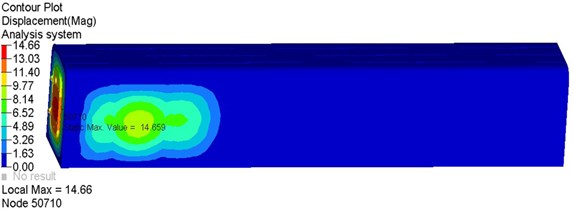
a)
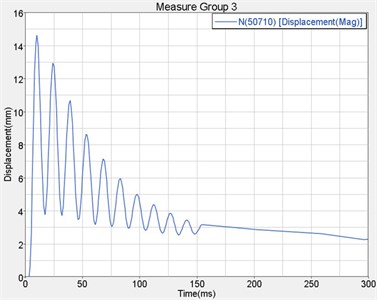
b)
The simulation results show that the maximum displacement of the whole cabin appeared in central on the underside of cabin during the impact process. The maximum displacement value is 14.57 mm, less than 20 mm. The maximum stress is 359 MPa, which means the position is in partial flange, less than the ultimate strength of material 470 MPa. The maximum stress acted on the entry door is 316 MPa, less than the yield strength of material 345 MPa. It occurred in the reinforcing ribs behind the entry door, and the maximum displacement is 14.66 mm. The maximum stress sustained by emergency escape hatch is 87.88 MPa, less than the yield strength of material 345 MPa, and the maximum displacement is 4.36 mm which is less than 15 mm [18]. The maximum stress bore by observation window is 30.96 MPa which is less than 43 MPa. The maximum relative displacement of sealing position in entry door and emergency escape hatch is 1.04 mm which is less than 2 mm. The results show that the refuge chamber met all the standard requirements of sufficient strength, stiffness and sealing, will be not damaged under the explosion shock wave [19].
Fig. 7Maximum stress moment contour and stress history graph
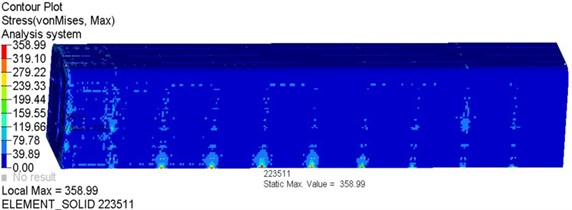
a)
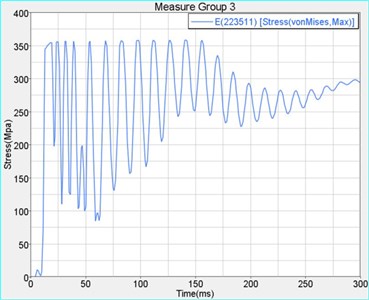
b)
Fig. 8Maximum relative displacement history graph of sealing position
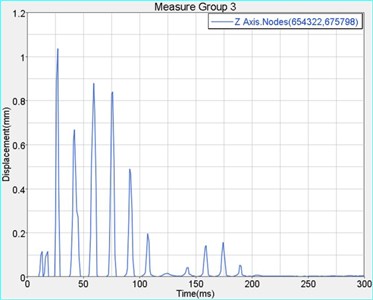
4. Conclusions
The numerical simulation and analysis of the coal mine refuge chamber have been done to ensure the refuge chamber would not be severely damaged when explosion happened. And the main conclusions drawn from the results are listed as follows:
Spectrum analysis of flow field pressure in the explosion shock wave was made with MATLAB, and the principal frequencies are obtained. The principal frequencies are 2 Hz, 4 Hz and 6 Hz.
Through analyzing the modal of refuge chamber under three constraint conditions, the first six natural frequencies and corresponding mode shapes are obtained. By comparing the three constraint methods, we found that constraints on both ends of each cabin are suitable for the refuge chamber. And the corresponding first sixth natural frequencies are as follows: 39.882 Hz, 71.564 Hz, 72.728 Hz, 74.178 Hz, 74.453 Hz, 75.435 Hz.
By comparing the results of spectrum analysis with natural frequencies, it can be seen that the first 6th natural frequencies of the refuge chamber with the method of constraints on both ends of each cabin are significantly larger than the principal frequency components of explosion shock wave, so resonance would not happen and the dynamic design of the refuge chamber is reasonable.
Besides, the strength of the coal mine refuge chamber was analyzed. During the process of impact, the maximum stress of refuge chamber is 359 MPa, the maximum displacement is 14.66 mm, and the maximum relative displacement is 1.04 mm, so all the parameters meet the standard requirements. It proved that the refuge chamber can maintain integrity under the impact of explosion shock wave. Therefore the refuge chamber has sufficient strength, stiffness and sealing.
At last, suggestions were presented based on the numerical analysis. It is proposed that a reasonable constraint should be chosen to avoid resonance. The flange should be reinforced. A topological optimization should be done to lighten the weight of the stiffener.
References
-
Józef Dubiński Sustainable development of mining mineral resources. Journal of Sustainable Mining, Vol. 12, 2013, p. 1-6.
-
Hirofumi Furukawa, Li Bingrui, Tomita Shinji Prevention of explosion in coal mine and management of coal mine gas. Journal of Coal Science and Engineering (China), Vol. 15, Issue 2, 2009, p. 215-219.
-
Wang S., Jin L. Z., L. J. The present situations of overseas mine emergency refuge chamber technology. Journal of Safety Science and Technology, Vol. 6, Issue 4, 2010, p. 119-123, (in Chinese).
-
Mejías Cristián, et al. Clinical response of 20 people in a mining refuge: study and analysis of functional parameters. Safety Science, Vol. 63, 2014, p. 204-210.
-
Si S. F., Wang K., Chen J., Pang Y. Q. Analysis on development status of coal mine refuge chamber. Coal Technology, Vol. 31, Issue 10, 2012, p. 88-90.
-
Valeria Di Sarli, Almerinda Di Benedetto, Gennaro Russo Using large eddy simulation for understanding vented gas explosions in the presence of obstacles. Journal of Hazardous Materials, Vol. 169, Issue 1, 2009, p. 435-442.
-
Costa B. J. A., Magalhães F., Cunha Á., Figueiras J. Rehabilitation assessment of a centenary steel bridge based on modal analysis. Engineering Structures, Vol. 56, 2013, p. 260-272.
-
Coal Mine Accident Analysis Report of China 2004-2009. State Administration of Work Safety, (in Chinese).
-
Zhang S. L., Zheng D. L., Hao Q. Structure Optimization Design Technology Based on Hyperworks. China Machine Press, Beijing, China, 2007, (in Chinese).
-
Brigham E. Oran The Fast Fourier Transform and Its Applications. Prentice Hall, Englewood Cliffs, NJ, Vol. 1, 1988.
-
Wang Y. G. Digital Signal Processing Using Matlab. Science Press, Beijing, China, 2007, (in Chinese).
-
Lian Y. H., Wang X. Y., He G., Chen Q. Spectrum analysis of blasting vibration signals. Mining Safety and Environmental Protection, Vol. 31, Issue 1, 2004, p. 49-52, (in Chinese).
-
Zhang L. Modal Analysis and Experiment. Tsinghua University Press, Beijing, China, 2011, (in Chinese).
-
Wen B. C., Liu S. Y., He Q. Mechanical Vibration Theory and Dynamic Design Method. China Machine Press, Beijing, China, 2001, (in Chinese).
-
Haiping Zhang, Liu Tongyan, Zhang Yuanci Torsional vibration calculation of coal mill transmission system. Cement Engineering, Vol. 5, 2010, p. 41-43.
-
Fasouletos M. A. Parametric Design of a Coal Mine Refuge Chamber. Master Thesis, West Virginia University, USA, 2007.
-
Mickey D. M. Analysis of Underground Coal Mine Refuge Shelters. Master Thesis, West Virginia University, USA, 2008.
-
State Administration of Work Safety Specifications for Coal Mine Mobile Refuge Chamber. China, 2011, (in Chinese).
-
Margolis Katherine A., Catherine Y. Kingsley Westerman, Kathleen M. Kowalski-Trakofler Underground mine refuge chamber expectations training: program development and evaluation. Safety Science, Vol. 49, Issue 3, 2011, p. 522-530.
About this article
The authors would like to express their special gratitude to the ZDKT12-01 Project of the State Key Laboratory of Explosion Science and Technology for the great financial support in this study.
