The effect of thermal source with mass diffusion in a transversely isotropic thermoelastic infinite medium

Abbas, Ibrahim A.

Journal of Measurements in Engineering

Browse Journal

Submit article

Published: 31 December 2014

Check for updates

The effect of thermal source with mass diffusion in a transversely isotropic thermoelastic infinite medium

Ibrahim A. Abbas¹

¹Mathematics Department, Faculty of Science and Arts – Khulais, King Abdulaziz University, Jeddah, Saudi Arabia

¹Department of Mathematics, Faculty of Science, Sohag University, Sohag, Egypt

Cite the article Download PDF

Downloads 1410

Abstract

The theory of generalized thermoelastic diffusion with relaxation times, in the context of Lord and Shulman theory, is used to investigate the thermoelastic diffusion problem in a transversely isotropic thermoelastic infinite medium with a cylindrical cavity. The surface of cavity is taken to be traction free and subjected to heating. The analytical solution in the Laplace transform domain is obtained by using the eigenvalue approach. The numerical results of displacement, temperature, mass concentration and stress as well as the chemical potential represented analytical and graphically. An appreciable effect of relaxation times is observed on various resulting quantities.

1. Introduction

The generalized theory of thermoelasticity is one of the modified versions of the classical uncoupled and coupled theory of thermoelasticity and has been developed in order to remove the paradox of the physically impossible phenomena of infinite velocity of thermal signals in the classical coupled thermoelasticity. The first of such modeling is the extended thermoelasticity theory (LS) of Lord and Shulman [1], who introduced the concept of thermal relaxation time into the classical Fourier law of heat conduction. Subsequently, modifying the stress versus strain relationship as well as the entropy relationship with relaxation time, Green and Lindsay [2] proposed the temperature rate dependent thermoelasticity (GL) theory. The theory was extended for anisotropic body by Dhaliwal and Sherief [3]. Recently, [4-13] have considered different problems by using the generalized thermoelasticity theories.

Diffusion can be defined as the random walk of an ensemble of particles, from regions of high concentration to regions of lower concentration. The studying of diffusion became increasingly important. This is due mainly to its many applications in geophysics and industrial applications. In integrated circuit fabrication, diffusion is used to introduce “dopants” in controlled amounts into the semiconductor substrate. In particular, diffusion is used to form the base and emitter in bipolar transistors, form integrated resistors, and form the source/drain regions in MOS transistors and dope poly-silicon gates in MOS transistors. The theory of thermoelastic diffusion is developed by [14-16]. In this theory, the coupled thermoelastic model is used. [17] developed the theory of generalized thermoelastic diffusion that predicts finite speeds of propagation for thermoelastic and diffusive waves. [18, 19] studied the theory of generalized thermoelastic diffusion in an infinite elastic body with a spherical cavity while [20, 21] investigated the diffusion in a generalized thermoelastic solid in an infinite body with a cylindrical cavity. The counterparts of our problem in the contexts of the thermoelasticity theories have been considered by using analytical and numerical methods [22-29].

In this paper, the thermoelastic interaction with mass diffusion in an infinite medium with a cylindrical cavity is investigated. Laplace transform techniques and eigenvalue approach are used. The physical explanations are given seriatim corresponding to the distributions of the considered physical variables obtained in this paper. An appreciable effect of relaxation times is observed on various resulting quantities.

2. Basic equations and problem formulation

Following Sherief et al. [17] and Abbas et al. [30], the governing equations for an anisotropic, homogeneous thermoelastic diffusion solid in the absence of body forces, heat source and mass diffusion source considered as:

– the equations of motion:

1

c_{i j k m} e_{k m, j} - a_{i j} T_{, j} - b_{i j} C_{, j} = ρ \frac{\partial^{2} u_{i}}{\partial t^{2}},

– the equation of heat conduction:

2

K_{i i} T_{, i i} = (\frac{\partial}{\partial t} + τ_{o} \frac{\partial^{2}}{\partial t^{2}}) (ρ c_{e} T + a_{k k} T_{0} e_{k k} + a T_{0} C),

– the equation of mass diffusion:

3

D_{i i} b C_{, i i} = (\frac{\partial}{\partial t} + τ_{1} \frac{\partial^{2}}{\partial t^{2}}) C + D_{i i} b_{k k} e_{k k, i i} + D_{i i} a T_{, i i},

– the constitutive equations:

4

σ_{i j} = c_{i j k m} e_{k m} - [a_{i j} (T - T_{0}) + b_{i j} C] δ_{i j},

5

P = - b_{k k} e_{k k} + b C - a (T - T_{0}),

6

e_{i j} = \frac{1}{2} (u_{i, j} + u_{j, i}),

where $c_{i j k m}$ are the elastic constants, $ρ$ is the density of the medium, $u_{i}$ are the components of displacement vector, $T$ is the temperature, $C$ is the concentration of diffusive material in the elastic material, $a_{i j}$ and $b_{i j}$ are the tensor of thermal and diffusion moduli respectively and $t$ is the time. $τ_{o}$ is the thermal relaxation time, $K_{i i}$ is the thermal conductivity, $c_{e}$ is the specific heat at constant strain, $e_{i j}$ are the components of strain tensor, $T_{0}$ is the reference temperature assumed to obey the inequality $|\frac{T - T_{0}}{T_{0}}| ≪ 1$ and $a$ is the measures of thermodiffusion effect. $τ_{1}$ is the diffusion relaxation time, $D_{i i}$ is the diffusion coefficient and $b$ is the measures of diffusive effects. $δ_{i j}$ is the Kronecker symbol, $σ_{i j}$ are the components of stress tensor and $P$ is the chemical potential.

Let us consider an elastic unbounded body with a cylindrical cavity occupying the region $R \leq r < \infty$ whose state can be expressed in terms of the space variable $r$ and the time $t$ . $(r, θ, z)$ are taken as the cylindrical coordinates with $z$ -axis aligned along the cylinder axis. We note that due to symmetry, the only non-vanishing displacement component is the radial one $u_{r} = u (r, t)$ . The strain tensor has the non-vanishing following components:

7

e_{r r} = \frac{\partial u}{\partial r}, e_{θ θ} = \frac{u}{r} .

Substituting for $e_{r r}$ , $e_{θ θ}$ into equations (4) and (5) we get:

8

σ_{r r} = c_{11} \frac{\partial u}{\partial r} + c_{12} \frac{u}{r} - a_{11} (T - T_{0}) - b_{11} C,

9

σ_{θ θ} = c_{12} \frac{\partial u}{\partial r} + c_{11} \frac{u}{r} - a_{11} (T - T_{0}) - b_{11} C,

10

P = - b_{11} (\frac{\partial u}{\partial r} + \frac{u}{r}) + b C - a (T - T_{0}),

where $a_{11} = (c_{11} + c_{12}) α_{t 1} + c_{13} α_{t 3}$ and $b_{11} = (c_{11} + c_{12}) α_{c 1} + c_{13} α_{c 3}$ , in which $α_{t 1}$ , $α_{t 3}$ are the coefficients of linear thermal expansion along the radial and tangential directions while and $α_{c 1}$ , $α_{c 3}$ are the coefficients of linear diffusion expansion along the radial and tangential directions. Thus, the equations (1), (2) and (3) can be written as:

11

c_{11} \frac{\partial e}{\partial r} - a_{11} \frac{\partial T}{\partial r} - b_{11} \frac{\partial C}{\partial r} = ρ \frac{\partial^{2} u}{\partial t^{2}},

12

K_{11} (\frac{\partial^{2} T}{\partial r^{2}} + \frac{1}{r} \frac{\partial T}{\partial r}) = (\frac{\partial}{\partial t} + τ_{o} \frac{\partial^{2}}{\partial t^{2}}) (ρ c_{e} T + a_{11} T_{0} e + a T_{0} C),

13

D_{11} b (\frac{\partial^{2} C}{\partial r^{2}} + \frac{1}{r} \frac{\partial C}{\partial r}) = (\frac{\partial}{\partial t} + τ_{1} \frac{\partial^{2}}{\partial t^{2}}) C + D_{11} b_{11} (\frac{\partial^{2} e}{\partial r^{2}} + \frac{1}{r} \frac{\partial e}{\partial r}) + D_{11} a (\frac{\partial^{2} T}{\partial r^{2}} + \frac{1}{r} \frac{\partial T}{\partial r}) .

Now, we introduce the following non-dimensional variables:

(r^{'}, u^{'}) = c ω (r, u), (t^{'}, {τ^{'}}_{o}, {τ^{'}}_{1}) = ω c^{2} (t^{'}, {τ^{'}}_{o}, {τ^{'}}_{1}), P^{'} = \frac{P}{b_{11}},

T' = \frac{a_{11} (T - T_{0})}{c_{11}}, ({σ'}_{r r}, {σ'}_{θ θ}) = \frac{(σ_{r r}, σ_{θ θ})}{c_{11}}, C' = \frac{b_{11} C}{c_{11}},

where $c^{2} = \frac{c_{11}}{ρ}$ and $ω = \frac{ρ c_{e}}{K_{11}}$ .

Using the above dimensionless variables, the equations (8)-(13), take the form where we have dropped the primes for convenience:

14

\frac{\partial e}{\partial r} - \frac{\partial T}{\partial r} - \frac{\partial C}{\partial r} = \frac{\partial^{2} u}{\partial t^{2}},

15

\frac{\partial^{2} T}{\partial r^{2}} + \frac{1}{r} \frac{\partial T}{\partial r} = (\frac{\partial}{\partial t} + τ_{o} \frac{\partial^{2}}{\partial t^{2}}) (T + β_{u} e + β_{c} C),

16

\frac{\partial^{2} C}{\partial r^{2}} + \frac{1}{r} \frac{\partial C}{\partial r} = ψ_{c} (\frac{\partial}{\partial t} + τ_{1} \frac{\partial^{2}}{\partial t^{2}}) C + ψ_{u} (\frac{\partial^{2} e}{\partial r^{2}} + \frac{1}{r} \frac{\partial e}{\partial r}) + ψ_{t} (\frac{\partial^{2} T}{\partial r^{2}} + \frac{1}{r} \frac{\partial T}{\partial r}),

17

σ_{r r} = \frac{\partial u}{\partial r} + γ \frac{u}{r} - T - C,

18

σ_{θ θ} = γ \frac{\partial u}{\partial r} + \frac{u}{r} - T - C,

19

P = χ_{c} C - e - χ_{t} T,

20

e = \frac{\partial u}{\partial r} + \frac{u}{r},

where $β_{u} = \frac{a_{11}^{2} T_{0}}{ρ c_{e} c_{11}}$ , $β_{c} = \frac{a T_{0} a_{11}}{ρ c_{e} b_{11}}$ , $γ = \frac{c_{12}}{c_{11}}$ , $ψ_{u} = \frac{b_{11}^{2}}{b c_{11}}$ , $ψ_{c} = \frac{1}{b D_{11} ω}$ , $ψ_{t} = \frac{a b_{11}}{b a_{11}}$ , $χ_{c} = \frac{b c_{11}}{b_{11}^{2}}$ , $χ_{t} = \frac{a c_{11}}{a_{11} b_{11}}$ .

The solution for the present problem is completed by the application of the initial and boundary conditions. The initial conditions can be expressed as:

21

u (r, 0) = \frac{\partial u (r, 0)}{\partial t} = 0, T (r, 0) = \frac{\partial T (r, 0)}{\partial t} = 0, C (r, 0) = \frac{\partial C (r, 0)}{\partial t} = 0 .

It is assumed that the inner surface of cavity is taken to be traction free and subject to a temperature which is decaying with time. The chemical potential is also assumed to be a known function of time on the inner surface of cavity. Therefore, the boundary conditions may be expressed as:

22

σ_{r r} (R, t) = 0, T (R, t) = T_{1} e^{- α t}, P (R, t) = P_{1} H (t), t > 0,

where $T_{1}$ and $P_{1}$ are constants, $α$ is an exponent of the decayed heat flux and $H (t)$ denotes the Heaviside unit step function.

3. Solution in the Laplace transform domain

Applying the Laplace transform for above equations define by the formula:

23

\bar{f} (s) = L [f (t)] = \int_{0}^{\infty} f (t) e^{- s t} d t .

Hence, the equations (14)-(22) take the form:

24

\frac{d^{2} \bar{u}}{d r^{2}} + \frac{1}{r} \frac{d \bar{u}}{d r} - \frac{\bar{u}}{r^{2}} - \frac{d \bar{T}}{d r} - \frac{d \bar{C}}{d r} = s^{2} \bar{u},

25

\frac{d^{2} \bar{T}}{d r^{2}} + \frac{1}{r} \frac{d \bar{T}}{d r} = s (1 + s τ_{o}) (\bar{T} + β_{u} \bar{e} + β_{c} \bar{C}),

26

\frac{d^{2} \bar{C}}{d r^{2}} + \frac{1}{r} \frac{d \bar{C}}{d r} = ψ_{c} s (1 + s τ_{1}) \bar{C} + ψ_{u} (\frac{d^{2} \bar{e}}{d r^{2}} + \frac{1}{r} \frac{d \bar{e}}{d r}) + ψ_{t} (\frac{d^{2} \bar{T}}{d r^{2}} + \frac{1}{r} \frac{d \bar{T}}{d r}),

27

{\bar{σ}}_{r r} = \frac{d \bar{u}}{d r} + γ \frac{\bar{u}}{r} - \bar{T} - \bar{C},

28

{\bar{σ}}_{θ θ} = γ \frac{d \bar{u}}{d r} + \frac{\bar{u}}{r} - \bar{T} - \bar{C},

29

\bar{P} = χ_{c} \bar{C} - \bar{e} - χ_{t} \bar{T},

30

\bar{e} = \frac{d \bar{u}}{d r} + \frac{\bar{u}}{r},

31

{\bar{σ}}_{r r} (R, s) = 0, \bar{T} (R, s) = \frac{T_{1}}{s + α}, \bar{P} (R, s) = \frac{P_{1}}{s} .

Differentiating equation (25) and (26) with respect to r and using equation (24) we get:

32

\frac{d^{2}}{d r^{2}} (\frac{d \bar{T}}{d r}) + \frac{1}{r} \frac{d}{d r} (\frac{d \bar{T}}{d r}) - \frac{1}{r^{2}} (\frac{d \bar{T}}{d r}) = ζ_{1} \bar{u} + ζ_{2} \frac{d \bar{T}}{d r} + ζ_{3} \frac{d \bar{C}}{d r},

33

\frac{d^{2}}{d r^{2}} (\frac{d \bar{C}}{d r}) + \frac{1}{r} \frac{d}{d r} (\frac{d \bar{C}}{d r}) - \frac{1}{r^{2}} (\frac{d \bar{C}}{d r}) = ζ_{4} \bar{u} + ζ_{5} \frac{d \bar{T}}{d r} + ζ_{6} \frac{d \bar{C}}{d r},

where $ζ_{1} = s^{2} β_{u} s (1 + s τ_{o}),$ $ζ_{2} = s (1 + s τ_{o}) (1 + β_{u}),$ $ζ_{3} = s (1 + s τ_{o}) (β_{u} + β_{c}),$ $ζ_{4} = \frac{s^{4} η_{u} + (ψ_{u} + ψ_{t}) ζ_{1}}{1 + ψ_{u}},$ $ζ_{5} = \frac{s^{2} ψ_{u} + (ψ_{u} + ψ_{t}) ζ_{2}}{1 + ψ_{u}},$ $ζ_{6} = \frac{s (1 + s τ_{1}) ψ_{c} + s^{2} ψ_{u} + (ψ_{u} + ψ_{t}) ζ_{3}}{1 + ψ_{u}}$ .

Equations (24), (32) and (33) can be written in a vector-matrix differential equation as follows [31]:

34

L \vec{V} = A \vec{V},

where $L \equiv \frac{d^{2}}{d r^{2}} + \frac{1}{r} \frac{d}{d r} - \frac{1}{r^{2}}$ , $\vec{V} = {[\bar{u} \bar{T} \bar{C} \frac{d \bar{u}}{d r} \frac{d \bar{T}}{d r} \frac{d \bar{C}}{d r}]}^{T}$ and $A = [\begin{array}{l} s^{2} & 1 & 1 \\ ζ_{1} & ζ_{2} & ζ_{3} \\ ζ_{4} & ζ_{5} & ζ_{6} \end{array}]$ .

4. Solution of the vector-matrix differential equation

Let us now proceed to solve equation (34) by the eigenvalue approach proposed by [31]. The characteristic equation of the matrix $B$ takes the form:

35

λ^{3} + λ^{2} (- ζ_{2} - ζ_{6} - s^{2}) + λ (ζ_{6} s^{2} - ζ_{1} - ζ_{4} - ζ_{3} ζ_{5} + ζ_{2} ζ_{6} + ζ_{2} s^{2})

+ ζ_{2} ζ_{4} - ζ_{3} ζ_{4} - ζ_{1} ζ_{5} + ζ_{1} ζ_{6} + ζ_{3} ζ_{5} s^{2} - ζ_{2} ζ_{6} s^{2} = 0 .

The roots of the characteristic equation (34) which are also the eigenvalues of matrix $A$ may be written in the form:

36

λ = λ_{1}, λ = λ_{2}, λ = λ_{3} .

The eigenvector $\vec{X} = {[X_{1}, X_{2}, X_{3}]}^{T}$ , corresponding to eigenvalue $λ$ can be calculated as:

37

X_{1} = ζ_{2} - ζ_{3} - λ,

38

X_{2} = - ζ_{1} - ζ_{3} (λ - s^{2}),

39

X_{3} = ζ_{1} + (ζ_{2} - λ) (λ - s^{2}) .

From equations (36)-(39), we can easily calculate the eigenvector ${\vec{X}}_{j}$ , corresponding to eigenvalue $ξ_{j}$ , $j = 1,2, 3$ . For further reference, we shall use the following notations:

40

{\vec{X}}_{1} = {[\vec{X}]}_{λ = λ_{1}}, {\vec{X}}_{2} = {[\vec{X}]}_{λ = λ_{2}}, {\vec{X}}_{3} = {[\vec{X}]}_{λ = λ_{3}} .

The solution of equation (34) which is bounded as $r \to \infty$ , is given by:

41

\vec{V} = {\vec{X}}_{1} B_{1} K_{1} (m_{1} r) + {\vec{X}}_{2} B_{2} K_{1} (m_{2} r) + {\vec{X}}_{3} B_{3} K_{1} (m_{3} r),

where $m_{1} = \sqrt{λ_{1}}$ , $m_{2} = \sqrt{λ_{2}}$ , $m_{3} = \sqrt{λ_{3}}$ , $K_{1}$ is the modified of Bessel’s function of order one, $B_{1}$ , $B_{2}$ and $B_{3}$ are constants to be determined from the boundary condition of the problem. Thus, the field variables can be written for $r$ and $s$ as:

42

\bar{u} (r, s) = x_{1}^{1} B_{1} K_{1} (m_{1} r) + x_{1}^{2} B_{2} K_{1} (m_{2} r) + x_{1}^{3} B_{3} K_{1} (m_{3} r),

43

\bar{T} (r, s) = - \frac{x_{2}^{1}}{m_{1}} B_{1} K_{0} (m_{1} r) - \frac{x_{2}^{2}}{m_{2}} B_{1} K_{0} (m_{2} r) - \frac{x_{2}^{3}}{m_{3}} B_{3} K_{0} (m_{3} r),

44

\bar{C} (r, s) = - \frac{x_{3}^{1}}{m_{1}} B_{1} K_{0} (m_{1} r) - \frac{x_{3}^{2}}{m_{2}} B_{1} K_{0} (m_{2} r) - \frac{x_{3}^{3}}{m_{3}} B_{3} K_{0} (m_{3} r),

45

{\bar{σ}}_{r r} (r, s) = B_{1} (\frac{(- m_{1}^{2} x_{1}^{1} + x_{2}^{1} + x_{3}^{1}) K_{0} (m_{1} r)}{m_{1}} + \frac{(η - 1) x_{1}^{1} K_{1} (m_{1} r)}{r})

+ B_{2} (\frac{(- m_{2}^{2} x_{1}^{2} + x_{2}^{2} + x_{3}^{2}) K_{0} (m_{2} r)}{m_{2}} + \frac{(η - 1) x_{1}^{2} K_{1} (m_{2} r)}{r})

+ B_{3} (\frac{(- m_{3}^{2} x_{1}^{3} + x_{2}^{3} + x_{3}^{3}) K_{0} (m_{3} r)}{m_{3}} + \frac{(η - 1) x_{1}^{3} K_{1} (m_{3} r)}{r}),

46

{\bar{σ}}_{θ θ} (r, s) = B_{1} (\frac{(- η m_{1}^{2} x_{1}^{1} + x_{2}^{1} + x_{3}^{1}) K_{0} (m_{1} r)}{m_{1}} - \frac{(η - 1) x_{1}^{1} K_{1} (m_{1} r)}{r})

+ B_{2} (\frac{(- η m_{2}^{2} x_{1}^{2} + x_{2}^{2} + x_{3}^{2}) K_{0} (m_{2} r)}{m_{2}} - \frac{(η - 1) x_{1}^{2} K_{1} (m_{2} r)}{r})

+ B_{3} (\frac{(- η m_{3}^{2} x_{1}^{3} + x_{2}^{3} + x_{3}^{3}) K_{0} (m_{3} r)}{m_{3}} - \frac{(η - 1) x_{1}^{3} K_{1} (m_{3} r)}{r}),

47

\bar{P} (r, s) = \frac{B_{1}}{m_{1}} (- ζ_{c} x_{3}^{1} + m_{1}^{2} x_{1}^{1} + ζ_{t} x_{2}^{1}) K_{0} (m_{1} r) + \frac{B_{2}}{m_{2}} (- ζ_{c} x_{3}^{2} + m_{2}^{2} x_{1}^{2} + ζ_{t} x_{2}^{2}) K_{0} (m_{2} r)

+ \frac{B_{3}}{m_{3}} (- ζ_{c} x_{3}^{3} + m_{3}^{2} x_{1}^{3} + ζ_{t} x_{2}^{3}) K_{0} (m_{3} r) .

To complete the solution we have to know the constants $B_{1}$ , $B_{2}$ and $B_{3}$ by using the boundary conditions (31) we can obtain:

48

(\begin{array}{l} B_{1} \\ B_{2} \\ B_{3} \end{array}) = {(\begin{array}{l} H_{11} & H_{12} & H_{13} \\ H_{21} & H_{22} & H_{23} \\ H_{31} & H_{32} & H_{33} \end{array})}^{- 1} (\begin{matrix} 0 \\ \frac{T_{1}}{s + α} \\ \frac{P_{1}}{s} \end{matrix}),

where:

H_{11} = \frac{(- m_{1}^{2} x_{1}^{1} + x_{2}^{1} + x_{3}^{1}) K_{0} (m_{1} R)}{m_{1}} + \frac{(η - 1) x_{1}^{1} K_{1} (m_{1} R)}{R},

H_{12} = \frac{(- m_{2}^{2} x_{1}^{2} + x_{2}^{2} + x_{3}^{2}) K_{0} (m_{2} R)}{m_{2}} + \frac{(η - 1) x_{1}^{2} K_{1} (m_{2} R)}{R},

H_{13} = \frac{(- m_{3}^{2} x_{1}^{3} + x_{2}^{3} + x_{3}^{3}) K_{0} (m_{3} R)}{m_{3}} + \frac{(η - 1) x_{1}^{3} K_{1} (m_{3} R)}{R},

\begin{array}{l} H_{21} = - \frac{x_{2}^{1}}{m_{1}} B_{1} K_{0} (m_{1} R), & H_{22} = - \frac{x_{2}^{2}}{m_{2}} B_{1} K_{0} (m_{2} R), & H_{23} = - \frac{x_{2}^{3}}{m_{3}} B_{3} K_{0} (m_{3} R), \end{array}

H_{31} = \frac{B_{1}}{m_{1}} (- ζ_{c} x_{3}^{1} + m_{1}^{2} x_{1}^{1} + ζ_{t} x_{2}^{1}) K_{0} (m_{1} R),

H_{32} = \frac{B_{2}}{m_{2}} (- ζ_{c} x_{3}^{2} + m_{2}^{2} x_{1}^{2} + ζ_{t} x_{2}^{2}) K_{0} (m_{2} R),

H_{33} = \frac{B_{3}}{m_{3}} (- ζ_{c} x_{3}^{3} + m_{3}^{2} x_{1}^{3} + ζ_{t} x_{2}^{3}) K_{0} (m_{3} R) .

5. Numerical inversion of the Laplace transform

In order to determine the conductive and thermal temperature, displacement and stress distributions in the time domain, the Riemann-sum approximation method is used to obtain the numerical results. In this method, any function in Laplace domain can be inverted to the time domain as:

49

f (t) = \frac{e^{κ t}}{t} [\frac{1}{2} \bar{f} (ε) + R e \sum_{n = 1}^{N} {(- 1)}^{n} \bar{f} (ε + \frac{i n π}{t})],

where $R e$ is the real part and $i$ is imaginary number unit. For faster convergence, numerous numerical experiments have shown that the value of $ε$ satisfies the relation $ε t \approx 4.7$ [32].

6. Numerical results and discussion

The material was chosen for purposes of numerical evaluations and the constants of the problem were taken as following [30]:

c_{11} = 18.78 \times 1 0^{10} \frac{K g}{m ∙ s^{2}}, c_{12} = 8.76 \times 1 0^{10} \frac{K g}{m ∙ s^{2}}, c_{13} = 8.0 \times 1 0^{10} \frac{K g}{m ∙ s^{2}},

c_{33} = 18.2 \times 1 0^{10} \frac{K g}{m ∙ s^{2}}, c_{44} = 5.06 \times 1 0^{10} \frac{K g}{m ∙ s^{2}}, T_{0} = . 293 \times 1 0^{3} K,

α_{1} = 2.98 \times 1 0^{- 5} K^{- 1}, α_{3} = 2.4 \times 1 0^{- 5} K^{- 1}, α_{1 c} = 2.1 \times 1 0^{- 4} m^{3},

α_{3 c} = 2.5 \times 1 0^{- 4} \frac{m^{3}}{K g}, a = 2.4 \times 1 0^{4} \frac{m^{2}}{s^{2} K g}, b = 13.2 \times 1 0^{5} \frac{m^{5}}{s^{2} K g},

ρ = 8.954 \times 1 0^{3} \frac{K g}{m^{3}}, K_{11} = 0.433 \times 1 0^{3} \frac{W}{m ∙ K}, K_{33} = 0.450 \times 1 0^{3} \frac{W}{m ∙ K},

D_{11} = 0.95 \times 1 0^{- 8} \frac{K g ∙ s}{m^{3}},

t = 0.3, R = 1, T_{1} = 1, τ_{o} = 0.01, τ_{1} = 0.02, p_{1} = 1 .

The effect of the exponent of the decayed heat flux $α$ on the distribution of all quantities through the thickness of the medium is investigated. The numerical technique outlined above was used to obtain the temperature, displacement, concentration, radial stress, hoop stress and the chemical potential distributions respect to distance $r$ at $t = 0.3$ for different values of the decayed heat flux $α$ . Figure 1 show the temperature decreases with the increase of the distance. It is noticed that the temperature always starts from different certain values according to the value of $α$ and terminates at the zero value. Of course, $T$ decreases with the increase of the exponent of the decayed heat flux $α$ . It is obvious from figure 2 that the displacement is negative at $r = R$ where its magnitude is maximum. The displacement increases from the negative value to a positive value. In the positive values, the displacement has a peak value that depends on the values of the decayed heat flux $α$ . Figure 3 show the distribution of concentration with distance $r$ . It is noticed that the concentration have a maximum magnitude at the boundary then decreases with the increasing of distance $r$ while it increase when increasing the decayed heat flux $α$ . Figure 4 display the variation of radial stress with distance $r$ for different values of $α$ . Its magnitude increases from zero to a maximum value after that decreases rapidly as $r$ increases and then the stress reduces to zero which agree with our theoretical boundary condition. Figure 5 display the variation of the hoop stress with the distance $r$ for different values of $α$ . Figure 6 show the variation of chemical potential with the distance $r$ . From figure 6, it is seen that the chemical potential starts with its maximum value, which satisfies the boundary conditions and decreases with the increasing of the distance $r$ .

Fig. 1The variation of temperature with distance r

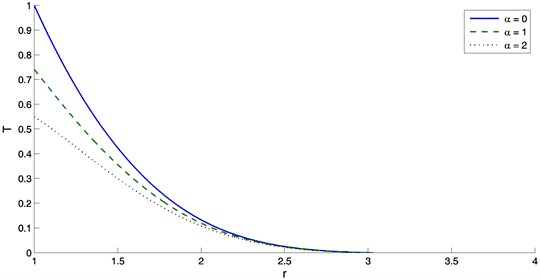
Fig. 2The variation of displacement with distance r

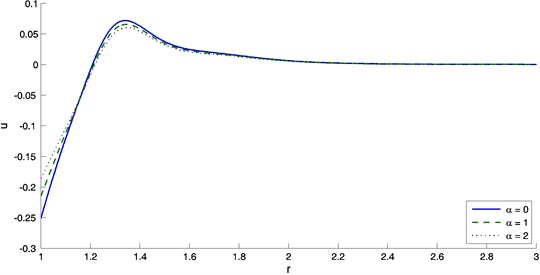
Fig. 3The variation of concentration with distance r

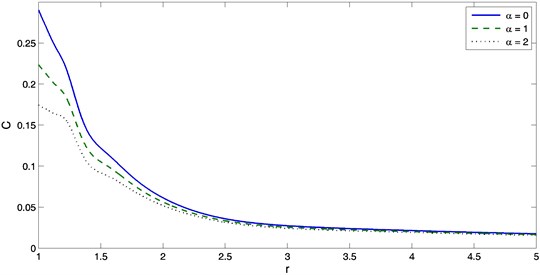
Fig. 4The variation of radial stress with distance r

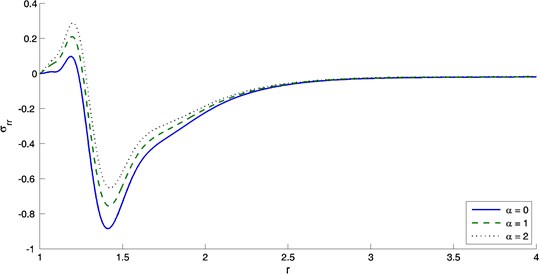
Fig. 5The variation of hoop stress with distance r

Fig. 6The variation of chemical potential with distance r

References

Lord H. W., Shulman Y. A generalized dynamical theory of thermoelasticity. Journal of the Mechanics and Physics of Solids, Vol. 15, Issue 5, 1967, p. 299-309.

Search CrossRef
Green A. E., LindsayK. A. Thermoelasticity. Journal of Elasticity, Vol. 2, Issue 1, 1972, p. 1-7.

Search CrossRef
Dhaliwal R. S., Sherief H. H. Generalized thermoelasticity for anisotropic media. Quarterly of Applied Mathematics. Vol. 38, 1980, p. 1-8.

Search CrossRef
Abbas I. A., Zenkour A. M. LS model on electro-magneto-thermoelastic response of an infinite functionally graded cylinder. Composite Structures, Vol. 96, 2013, p. 89-96.

Search CrossRef
Abbas I. A., Othman M. I. A. Generalized thermoelasticity of the thermal shock problem in an isotropic hollow cylinder and temperature dependent elastic moduli. Chinese Physics B, Vol. 21, Issue 1, 2012.

Search CrossRef
Abbas I. A., Othman M. I. A. Plane waves in generalized thermo-microstretch elastic solid with thermal relaxation using finite element method. International Journal of Thermophysics, Vol. 33, Issue 12, 2012, p. 2407-2423.

Search CrossRef
Abbas I. A. Generalized magneto-thermoelastic interaction in a fiber-reinforced anisotropic hollow cylinder. International Journal of Thermophysics, Vol. 33, Issue 3, 2012, p. 567-579.

Search CrossRef
Abd-alla A. N., Abbas I. A. A problem of generalized magnetothermo-elasticity for an infinitely long, perfectly conducting cylinder. Journal of Thermal Stresses, Vol. 25, Issue 11, 2002, p. 1009-1025.

Search CrossRef
Ezzat M. A., YoussefH. M. State space approach for conducting magneto-thermoelastic medium with variable electrical and thermal conductivity subjected to ramp-type heating. Journal of Thermal Stresses, Vol. 32, Issue 4, 2009, p. 414-427.

Search CrossRef
Ezzat M., Zakaria M., Abdel-BaryA. Generalized thermoelasticity with temperature dependent modulus of elasticity under three theories. Journal of Applied Mathematics and Computing, Vol. 14, Issue 1-2, 2004, p. 193-212.

Search CrossRef
Sherief H. H., Youssef H. M. Short time solution for a problem in magnetothermoelasticity with thermal relaxation. Journal of Thermal Stresses, Vol. 27, Issue 6, 2004, p. 537-559.

Search CrossRef
Sherief H. H., Ezzat M. A. A thermal-shock problem in magneto-thermoelasticity with thermal relaxation. International Journal of Solids and Structures, Vol. 33, Issue 30, 1996, p. 4449-4459.

Search CrossRef
Sherief H. H., Anwar M. N. State-space approach to two-dimensional generalized thermoelasticity problems. Journal of Thermal Stresses, Vol. 17, Issue 4, 1994, p. 567-586.

Search CrossRef
Nowacki W. Dynamic problems of thermodiffusion in elastic solids. Proceedings of Vibration Problems, 1974.

Search CrossRef
Nowacki W. Dynamical problem of thermodiffusion in solids. I. Academie Polonaise des Sciences, Bulletin, Serie des Sciences Techniques, Vol. 22, Issue 1, 1974, p. 43.

Search CrossRef
Nowacki W. Dynamical problem of thermodiffusion in solids. II. Academie Polonaise des Sciences, Bulletin, Serie des Sciences Techniques, Vol. 22, Issue 3, 1974, p. 129.

Search CrossRef
Sherief H. H., Hamza F. A., Saleh H. A. The theory of generalized thermoelastic diffusion. International Journal of Engineering Science, Vol. 42, Issue 5-6, 2004, p. 591-608.

Search CrossRef
Aouadi M. A problem for an infinite elastic body with a spherical cavity in the theory of generalized thermoelastic diffusion. International Journal of Solids and Structures, Vol. 44, Issue 17, 2007, p. 5711-5722.

Search CrossRef
Elhagary M. A. Generalized thermoelastic diffusion problem for an infinite medium with a spherical cavity. International Journal of Thermophysics, Vol. 33, Issue 1, 2012, p. 172-183.

Search CrossRef
Sharma J. N., Kumari N., Sharma K. K. Diffusion in a generalized thermoelastic solid in an infinite body with a cylindrical cavity. Journal of Applied Mechanics and Technical Physics, Vol. 54, Issue 5, 2013, p. 819-831.

Search CrossRef
Zenkour A. M., Mashat D. S., Abouelregal A. E. Generalized thermodiffusion for an unbounded body with a spherical cavity subjected to periodic loading. Journal of Mechanical Science and Technology, Vol. 26, Issue 3, 2012, p. 749-757.

Search CrossRef
Zenkour A. M., Abbas I. A. Free vibration analysis of doubly convex/concave functionally graded sandwich beams. Journal of Vibroengineering, Vol. 16, Issue 6, 2014, p. 2747-2755.

Search CrossRef
Zenkour A. M., Abbas I. A. Magneto-thermoelastic response of an infinite functionally graded cylinder using the finite element model. Journal of Vibration and Control, Vol. 20, Issue 12, 2014, p. 1907-1919.

Search CrossRef
Abbas I. A., Kumar R. Interaction due to a mechanical source in transversely isotropic micropolar media. Journal of Vibration and Control, Vol. 20, Issue 11, 2014, p. 1607-1621.

Search CrossRef
Abbas I. A. A GN model based upon two-temperature generalized thermoelastic theory in an unbounded medium with a spherical cavity. Applied Mathematics and Computation, Vol. 245, 2014, p. 108-115.

Search CrossRef
Abbas I. A. Fractional order GN model on thermoelastic interaction in an infinite fibre-reinforced anisotropic plate containing a circular hole. Journal of Computational and Theoretical Nanoscience, Vol. 11, Issue 2, 2014, p. 380-384.

Search CrossRef
Abbas I. A. A GN model for thermoelastic interaction in an unbounded fiber-reinforced anisotropic medium with a circular hole. Applied Mathematics Letters, Vol. 26, Issue 2, 2013, p. 232-239.

Search CrossRef
Othman M. I. A., Abbas I. A. Effect of rotation on plane waves at the free surface of a fibre-reinforced thermoelastic half-space using the finite element method. Meccanica, Vol. 46, Issue 2, 2011, p. 413-421.

Search CrossRef
Abbas I. A. Natural frequencies of a poroelastic hollow cylinder. Acta Mechanica, Vol. 186, Issue 1-4, 2006, p. 229-237.

Search CrossRef
Abbas I. A., Kumar R., Chawla V. Response of thermal source in a transversely isotropic thermoelastic half-space with mass diffusion by using a finite element method. Chinese Physics B, Vol. 21, Issue 8, 2012.

Search CrossRef
Das N. C., Lahiri A., Giri R. R. Eigenvalue approach to generalized thermoelasticity. Indian Journal of Pure and Applied Mathematics, Vol. 28, Issue 12, 1997, p. 1573-1594.

Search CrossRef
Tzou D. Y. Macro-to Micro-Scale Heat Transfer: the Lagging Behavior. CRC Press, 1996.

Search CrossRef

About this article

Received

20 October 2014

Accepted

12 December 2014

Published

31 December 2014

Keywords

eigenvalue approach

Laplace transform

Lord and Shulman theory

thermoelastic diffusion

Acknowledgements

This project was funded by Saudi Basic Industries Corporation (SABIC) and the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under Grant No. (MS/15/181/1434). The authors, therefore, acknowledge with thanks SABIC and DSR technical and financial support.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.