Abstract
Hydraulic pump is regarded as the heart of hydraulic system. Achieving the real-time fault diagnosis of hydraulic pump is of great importance for the maintenance of the entire system. An accurate fault clustering solution with self-adaptive signal processing is needed for extracting performance degradation information hidden in the nonlinear and non-stationary signals of hydraulic pumps. Therefore, a fault diagnosis approach based on ensemble empirical mode decomposition (EEMD), kernel principal component analysis (KPCA), and learning vector quantization (LVQ) network is proposed in this study. First, EEMD is employed to acquire more significant intrinsic mode functions (IMFs), thus overcoming the drawback of empirical mode decomposition, and further extracting the energy values of each IMF to form the feature vector. Second, KPCA, a nonlinear dimension reduction method, is used to remove redundancies of the extracted feature vector for high accuracy of fault diagnosis. Finally, LVQ is employed to classify faults based on the reduced feature vector. The efficiency and accuracy of the proposed method is validated by a case study based on the vibration dataset of a plunger pump.
1. Introduction
Hydraulic system has been widely used in the areas of aeronautics, astronautics, metallurgy, etc. As the power source of a hydraulic system, hydraulic pump is often regarded as the heart of the system. Operating condition of hydraulic pump has a direct impact on the performance of the hydraulic system and even on the entire system [1]. Therefore, it would be particularly important to realize real-time fault diagnosis of hydraulic pump [2].
As a rotating machinery, vibration characteristics of hydraulic pump will changes with its performance. Therefore, reliable feature representative of the pump condition can be extracted by the processing and analysis of the vibration signal measuring on the pump [3]. However, due to the complexity of the hydraulic pump failure mechanism and operating environment, vibration signals of abnormal hydraulic pump are nonlinear and non-stationary, and normally buried in the noise signals. It is difficult to extract effective fault characteristics by using common signal processing methods. Wavelet-based method has been widely used as an effective way to process nonlinear and non-stationary signal. But it has some inevitable deficiencies such as interference terms, border distortion and energy leakage [4]. Empirical mode decomposition (EMD), proposed by Huang et al., was then demonstrated to be superior to wavelet analysis in many applications [5]. Based on local properties of the signal, EMD can decompose any complicated data set in to a finite number of intrinsic mode functions (IMF), which represents a simple oscillatory mode. But one of the major drawbacks of EMD is the problem of mode mixing, which will debase the physical meaning of IMF. To solve this problem, EEMD was proposed for substantial improvement over the original EMD by using noise assisted data analysis [6].
Neural network is broadly used as an intelligent classifier to recognize fault patterns. Back-propagation (BP) network is one of the most widely used neural network in many areas. But it has some shortage in convergence rate and training time [7]. Learning Vector Quantization was introduced by Teuvo Kohonen as a supervised counterpart of vector quantization systems, which applies a winner-take-all Hebbian learning-based approach [8]. LVQ network has a fast convergence rate, short training time, and a simple but accurate output, which is good for real-time fault diagnosis [7].
Training a neural network with high-dimensional data is a time-consuming process. To improve the real-time performance and accuracy of fault diagnosis, dimension reduction methods are usually applied for feature reduction. Principal Component Analysis (PCA) and Fisher Discriminant Analysis (FDA) are both commonly used dimension reduction method. However, linear correlation among the variables is assumed in these methods, which degrades their performance in nonlinear systems. Kernel Principal Component Analysis (KPCA) was proposed by Schölkopf et al. as a nonlinear form of Principal Component Analysis [9]. By computing principal components in high dimensional feature spaces which is related to input space by some nonlinear map, KPCA has a better performance in nonlinear systems, for example, hydraulic system.
Aiming at processing the nonlinear and non-stationary vibration signals and acquiring accurate fault diagnosis, an approach based on EEMD, KPCA, and LVQ is proposed in this study.
2. Methodology
2.1. Procedure of the proposed method
The fault diagnosis method proposed in this paper can be summarized as three parts (Fig. 1):
a) Feature Extraction: EEMD is employed to decompose the original signal into finite IMFs. Energy values of the IMFs are extracted to form the feature vector.
b) Feature Reduction: KPCA is employed to reduce the dimension of the feature vector. Only the principal components which contain most of the information are selected for further analysis.
c) Fault Diagnosis: the reduced feature vectors are sent to the LVQ network for training. With the trained LVQ network, fault mode of the current sample can be judged.
Fig. 1Procedure of the proposed approach
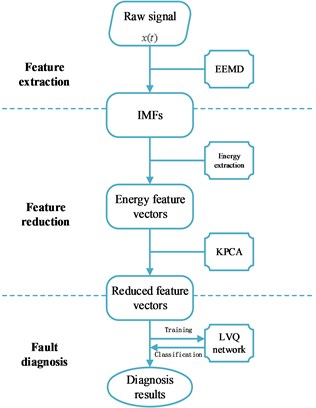
Fig. 2Test plunger pump rig

2.2. Signal processing by ensemble empirical mode decomposition
EMD has been widely used in fault diagnosis as an effective self-adaptive analysis tool for non-stationary and nonlinear signals [5]. Based on local properties of the signal, EMD can decompose any complicated data set in to a finite number of IMFs which represents a simple oscillatory mode. But one of the major drawbacks of EMD is the problem of mode mixing, which will debase the physical meaning of IMF. To solve this problem, EEMD was proposed for substantial improvement over the original EMD by using noise assisted data analysis [6].
The principle of the EEMD can be described as follows. First, by adding Gaussian random white noise sequence, which is uniformly distributed and its standard deviation of amplitude is constant, the original signal generate enough extreme point to avoid mode mixing. Second, apply EMD decomposition to the signal with Gaussian white noise to acquire their corresponding IMFs. Since the statistical mean of uncorrelated random sequence is zero, calculate the ensemble average of the corresponding IMFs to eliminate the effect of Gaussian white noise on the true IMFs. At last, the ensemble mean is treated as the true IMF. As is described above, it is not hard to find that EEMD decomposition does avoid mode mixing while eliminate the effect of adding Gaussian white noise.
The EEMD algorithm is detailed as follows:
1) Add a white noise signal to the targeted signal :
where represents the noise-added signal of the th trial, 1, 2, 3,..., and is the initialized number of the trial.
2) Decompose the noise-added signal into a finite number of IMFs and the residue using EMD method:
where is the number of IMFs, and 1, 2, 3,..., .
3) Proceed step (1) and (2) for times, and each time add a different random white noise signal.
4) Calculate the ensemble means of each corresponding IMF for the trials:
5) Report (1, 2, 3,..., ) as the final IMFs.
2.3. Feature extraction by energy extraction
When different faults appear in hydraulic pump, the corresponding resonance frequency components appear in the vibration signals, and the energy of fault vibration signal in each IMF changes with the frequency distribution. In this paper, energy of each IMF is extracted as the fault feature. (Assuming that the energy of residual energy can be ignored.) Each IMF is processed with:
where is the energy of each IMF, normalized as below:
where is the normalized feature vector, which carries the information of signal.
2.4. Dimension reduction of feature vector by kernel principal component analysis
KPCA was firstly proposed by Schölkopf et al as a nonlinear form of Principal Component Analysis [9]. The main idea of KPCA is to compute principal components in high dimensional feature spaces, which is related to input space by some nonlinear map, by using integral operator kernel functions. Its algorithm can be briefly described as follows.
Assuming that the training data for KPCA is (1, 2, 3,...). is a nonlinear function that maps the input vectors to the feature space Assuming that . So the covariance matrix of in the feature space can be given as:
The nonzero eigenvalues of the covariance matrix is , and the eigenvector is . , and can be expanded by as:
Define a size kernel matrix in which the coefficients can be obtained. , where represents the dot product operator. The principal components can be extract by calculate the projection of a vector onto eigenvector in feature space :
2.5. Fault diagnosis based on learning vector quantization network
LVQ, proposed by Teuvo Kohonen, is regarded as a special artificial neural network, which serves as a supervised counterpart of vector quantization systems and applies a winner-take-all Hebbian learning algorithm [8]. An LVQ network consists of three layers: the input layer that includes one neuron for each parameter; the competitive layer of the hidden layer in which learning and classification operates; and the output layer comprises only one neuron for each class. A weight matrix is designed between the input layer and the hidden layer, which includes the classification information.
3. Experimental verification
3.1. Experiment setup
In this study, several groups of data generated from a test plunger pump fig were employed to verify the effectiveness and practicality of the proposed method (Fig. 2). Two commonly occurring faults, slipper loose and valve plate wear, were injected into the test plunger pump fig. The vibration signals were acquired by an acceleration transducer from the end face of the plunger pump. In the experiment, the motor speed was 528 r/min, and the sampling rate was 1000 Hz.
3.2. Feature extraction
In the analysis, 300 groups of data are selected to be trained from three different conditions (normal, slipper loose, and valve plate wear), together with another 30 groups of data selected from similar conditions as the testing groups.
Each raw data is decomposed into 8 IMFs by EEMD (Fig. 3). Then, energy value of each IMF is extracted to form the initial feature vector.
Fig. 3A sample of decomposition results with EEMD
3.3. Feature reduction
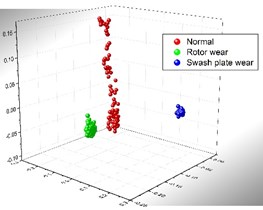
The characteristic matrix, composed of 300 groups of eigenvector, is processed with KPCA to obtain the principal components as well as their contributions (Fig. 4(a)). As is shown in the figure, the contribution of first two principal components has reached 0.91 while the first three reached 0.98. In order to increase efficiency, only the first three principal components which contribute 98 % of the information are used as eigenvector. The distribution of feature points are directly shown in Fig. 4(b).
Fig. 4a) Contributions of principal components, b) distribution of feature points

a)
b)
3.4. Fault diagnosis
The reduced 300×3 characteristic matrix is sent to LVQ network for training. The learning function of the network is LVQ2. Normal condition is targeted as (1, 0, 0), while swash plate wear as (0, 1, 0) and rotor wear as (0, 0, 1).
The 30 groups of testing data are also processed by EEMD and KPCA with the same principle as training data. The 30 feature vectors extracted from testing data are sent to the trained LVQ network. The diagnosis results can be judged from the outputs of the LVQ network (partly described in Table 1).
In the results, all 30 outputs are correctly corresponding to the real fault modes, which means the accuracy rate of diagnosis is 100 %. The diagnosis result reveals the effectiveness and accuracy of the proposed approach.
Table 1Diagnosis results
No. | 1 | 2 | … | 15 | 16 | … | 29 | 30 |
Fault modes | Normal | Normal | … | Swash plate wear | Swash plate wear | … | Rotor wear | Rotor wear |
Feature vectors | (–0.1541, –0.0691, 0.1273) | (–0.2145, –0.0120, –0.0662) | … | (–0.0111, –0.1853, –0.0283) | (0.0279, –0.2138, –0.0239) | … | (0.2080, –0.0416, –0.0089) | (0.1807, 0.03340, –0.0248) |
LVQ outputs | (1,0,0) | (1,0,0) | … | (0,1,0) | (0,1,0) | … | (0,0,1) | (0,0,1) |
4. Conclusions
To address the problem existing in fault diagnosis for the nonlinear and non-stationary vibration signal of a hydraulic pump, an approach combining EEMD-KPCA with LVQ is proposed in this study. EEMD was applied to decompose the original signals into a finite number of IMFs with certain physical significance. Energy values of the IMFs were extracted as feature vector, which was further reduced by using KPCA. The reduced feature vector was then input to the trained LVQ network. Two commonly occurring hydraulic pump faults were used to validate the effectiveness of the proposed approach.
References
-
Lu C., Ma N., Wang Z. Fault detection for hydraulic pump based on chaotic parallel RBF network. Journal on Advances in Signal Processing, 2011, p. 1-10.
-
Hancock K. M., Zhang Q. A hybrid approach to hydraulic vane pump condition monitoring and fault detection. Transactions of the ASABE, Vol. 49, Issue 4, 2006, p. 1203-1211.
-
Mollazade K., Ahmadi H., Omid M., et al. An intelligent combined method based on power spectral density, decision trees and fuzzy logic for hydraulic pumps fault diagnosis. International Journal of Intelligent Systems and Technologies, Vol. 3, Issue 4, 2008, p. 251-263.
-
Cheng G., Cheng Y., Shen L., et al. Gear fault identification based on Hilbert-Huang transform and SOM neural network. Measurement, Vol. 46, Issue 3, 2013, p. 1137-1146.
-
Lu C., Yuan H., Tang Y. Bearing performance degradation assessment and prediction based on EMD and PCA-SOM. Journal of Vibroengineering, Vol. 16, Issue 3, 2014.
-
Wu Z., Huang N. E. Ensemble empirical mode decomposition: a noise-assisted data analysis method. Advances in Adaptive Data Analysis, 2009, p. 1-41.
-
Yang H. T., Liao C. C., Chou J. H. Fuzzy learning vector quantization networks for power transformer condition assessment. Dielectrics and Electrical Insulation, Vol. 8, Issue 1, 2001, p. 143-149.
-
Kohonen T., Maps S. O. Springer series in information sciences. Self-Organizing Maps, Vol. 30, 1995.
-
Schölkopf B., Smola A., Müller K. R. Kernel principal component analysis. Artificial Neural Networks, Berlin, 1997, p. 583-588.
About this article
This research was supported by the National Natural Science Foundation of China (Grant No. 61074083, 50705005, and 51105019), and by the Technology Foundation Program of National Defense (Grant No. Z132013B002).
