Abstract
As a key component of rotating machineries, fault diagnosis for planetary gearbox is very difficult compared to the fixed shaft gearbox. It is becoming a hot research topic recent years. Different fault type has different vibration characteristics. Different from the traditional signal analysis methods, morphological gradient filters are used to extract the fault frequencies in this paper. Planetary gearbox experiment signals are used to validate the proposed method.
1. Introduction
Planetary gearbox contains sun gear, planet gears, planet carrier and ring gear. It is increasingly used in the drive train of many kinds of machinery in recent years, such as wind turbine, helicopter, crane and so on, due to they can provide a larger transmission ratio in a more compact package than traditional fixed shaft gearbox. A failure of gearbox may cause shutdown of the entire train and result in major economic losses. Therefore, the fault diagnosis of the planetary gearbox is crucial to prevent the mechanical system from malfunction.
The function of planetary gearbox is to transfer torque and power from the central sun gear through the planets to the planet carrier and from the planet carrier to the output shaft. Because the complicated structure, the transfer paths from meshing point to sensor when acquire vibration signal are also not simple. The complicated transfer paths bring a series of dilemmas to fault diagnosis of planetary gearbox. The first is that the amplitude of the acquired signal is weakened. Another one is that the acquired signal is non-stationary and non-linear. In addition, planetary gearbox usually works in the condition which is low speed and weight load, so the characteristic frequency is not easy to distinguish due to the noise signal. To solve these problems, many researchers and organizations have made great efforts.
Samuel and Pines [1] reviewed the research state in vibration-based techniques for helicopter transmission diagnostics. They illustrated the importance of condition monitoring for gearbox from the view of cost and safety. Lei et al. [2] analyzed the characteristics and difficulty of planetary gearbox fault diagnosis in the general and reviewed the inland and overseas research advances from dynamic modeling and signal processing, then pointed the existing key problems in the current research and the approaches to these problems were discussed at last. Feng and Zuo [3] constituted the vibration signal models for fault diagnosis of planetary gearboxes with considering amplitude modulation and frequency modulation effects. Feng et al. [4] analyzed the spectral characteristics of distributed fault and localized fault, respectively. And they implemented amplitude modulation and frequency modulation analysis for fault diagnosis of planetary gearboxes.
Vibration signal analyzing has been a useful technique for fault diagnosis of gearboxes for many decades because vibration signal contains abundant fault information. Samuel and Pines [5] and McFadden [6, 7] separate the vibration signal of planet and sun gears used time domain averaging. Usually, conventional signal processing techniques are also suitable and effective for fault diagnosis, such as Fourier transform [8]. In recent years, adaptive methods are popular increasingly. Samuel and Pines [9] proposed a constrained adaptive lifting wavelet transform to analyze individual tooth mesh waveforms to detect damage in helicopter planetary transmissions. Fan and Zuo [10] proposed a new method that combined Hilbert transform and wavelet packet transform to detect gear faults.
Due to the structure of planetary gearbox is very complicate, many different feature frequencies can be depicted in FFT spectrum. In addition, noise interference is very serious because of the work condition which is low speed and weight load. Traditional frequency analysis methods are very hard to exact the fault frequencies. This paper solves this problem using morphological gradient filters and the effectiveness of this method has been validated.
2. Morphological gradient filters
Mathematical morphology filters was originally put forward by Matheron and Serra as an image processing methodology in 1964. The basic thought of it is to modify the shape of a signal by pre-defined structuring element so that achieve the aim of extract feature and decrease noise. Generally, morphology filters include two kinds of basic algorithms: dilation and erosion which are defined as follows [11, 12].
Assume , and , () are input signal and structuring element, respectively. Then the dilation and erosion algorithms are defined as:
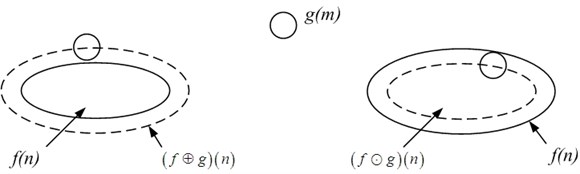
where and represent the algorithms of dilation and erosion, respectively. The diagram of dilation and erosion algorithm is as Fig. 1.
Fig. 1Diagram of dilation and erosion algorithm
And the algorithms of opening and closing are based on the dilation and erosion algorithm and defined as following:
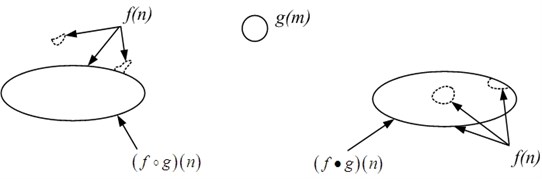
where “” means the opening algorithm and “” represents the closing algorithm. The diagram of opening and closing algorithm is as Fig. 2.
Fig. 2Diagram of opening and closing algorithm
Dilation algorithm can eliminate plus pulse and sharp minus pulse. Erosion algorithm is opposite, it can eliminate minus pulse and sharp plus pulse. Opening algorithm retain minus pulse while eliminate plus pulse, and closing algorithm eliminate minus pulse and keep plus pulse. The above four kinds of basic morphology algorithms can only extract one of plus and minus pulse information from signal. However, the general condition in practical is that plus and minus pulse are existent at the same time. So, morphological gradient filters which are constructed based on the combination of the four kinds of basic morphology filters are needed. Two types of morphological gradient filters, morphological dilation-erosion gradient filter () and morphological closing-opening gradient filter (), can be defined as follows:
3. Planetary gearbox fault experiment
An introduced fault experiment of planetary gearbox was implemented rely on the RCM laboratory of Mechanical Engineering College in order to validate the effectiveness of the method this paper proposed. The experimental system consists of a test planetary gearbox, a 4 KW three phase asynchronous drive motor, a speed and torque sensor to acquire the speed and torque information and a magnetic powder brake to provide load. And between the two of them is connected by coupling, as shown in Fig. 3.
Fig. 3Planetary gearbox experimental system

The introduced fault is seed wear fault on one tooth of sun gear, planet gear and ring gear. This paper chooses the sun gear which meshes with three planet gears at the same time as example. Fig. 4(a) shows the sun gear after seeded the wear fault. Four accelerometers are mounted on the planetary gearbox casing by glue, wherein accelerometer 1 and 2 are mounted on the input side of the gearbox, accelerometer 3 is on the top of the casing and accelerometer 4 is fixed on the output side. The specific location of every accelerometer is as depicted as Fig. 4(b). And the configuration parameters of planetary gearbox can be seen in Table 1.
Fig. 4a) Sun gear with seeded wear fault, b) the mounted location of accelerometers

a)

b)
The input shaft, shaft 1, is driven by the motor at a speed of 1200 rpm. And the sun gear is machined on it. The magnetic powder brake provide three different kinds of loads, they are 0 Nm, 0.6 Nm and 1.2 Nm. The characteristic frequencies of shafts and gears are calculated in Table 2.
Table 1Planetary gearbox configuration parameters
Gear | Sun gear | Planet gear (number) | Ring gear |
Number of teeth | 13 | 64 (3) | 146 |
Table 2Characteristic frequencies of shafts and gears
Characteristic frequencies | Meshing frequency | Rotating frequency of shaft 1 | Rotating frequency of shaft 2 | Fault frequency of sun gear | Fault frequency of planet gear | Fault frequency of ring gear |
Value | 238.738 | 20 | 1.635 | 55.093 | 3.730 | 4.906 |
4. Fault diagnosis and discussion
This section will analyze the signal acquire from the experiment in Section 3 in order to validate the ability of extract pulse information of the above morphological filters. Choose the work condition of 1200 rpm and 0.6 Nm as example.
Fig. 5 shows the envelope spectrum of sun gear wear fault, 3 multiple fault frequency can be seen. However, the noise is still very serious though in experiment environment.
Fig. 5Envelope spectrum of sun gear wear fault
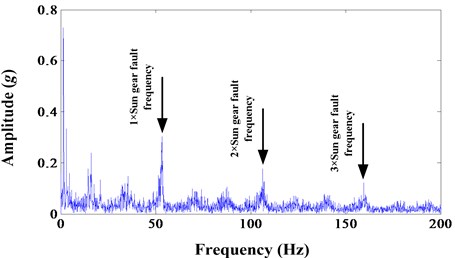
Fig. 6-11 are the results of morphological dilation, erosion, opening and closing, respectively. The frequency spectrums of them are also shown as follows.
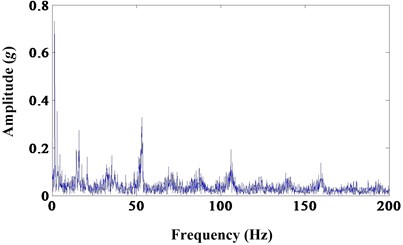
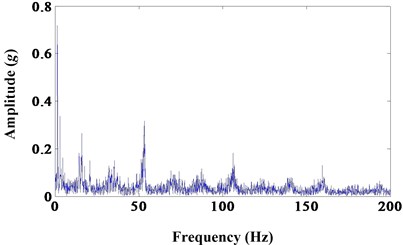
All of the six morphological filters can extract the fault frequency and decrease noise contrast to the envelope spectrum of sun gear wear fault. But the later two morphological filters, dilation-erosion and opening-closing, can extract the fault frequency with high amplitude. And morphological dilation-erosion gradient is more sensitive than opening-closing. This is in experiment environment and it will be more obvious in practice.
Fig. 6a) Results of morphological dilation; b) frequency spectrum
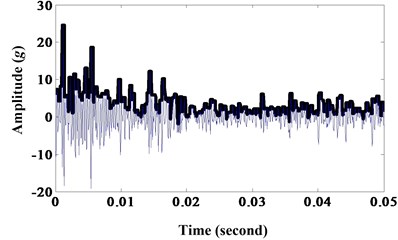
a)
b)
Fig. 7a) Results of morphological erosion; b) frequency spectrum
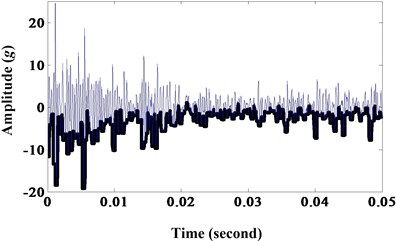
a)
b)
Fig. 8a) Results of morphological closing; b) frequency spectrum
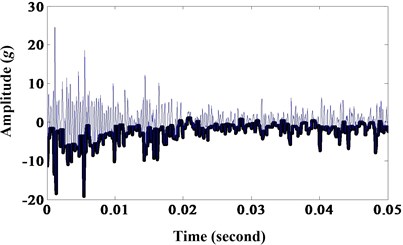
a)
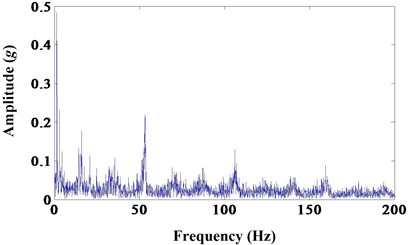
b)
Fig. 9a) Results of morphological opening; b) frequency spectrum
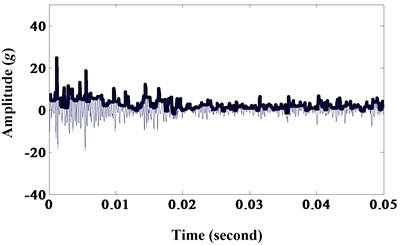
a)
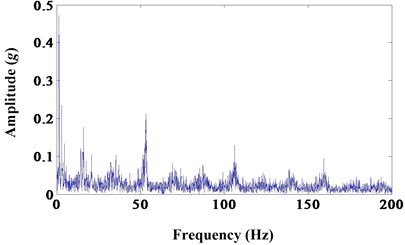
b)
Fig. 10a) Results of morphological dilation-erosion gradient; b) frequency spectrum
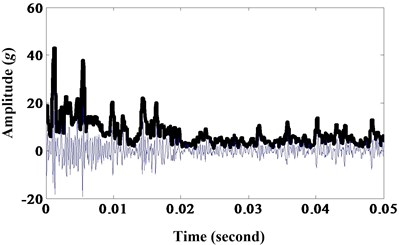
a)
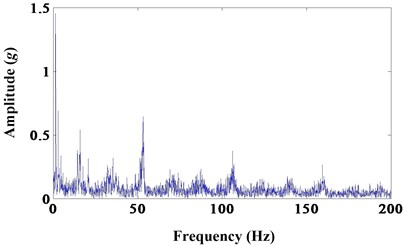
b)
Fig. 11a) Results of morphological opening-closing gradient; b) frequency spectrum
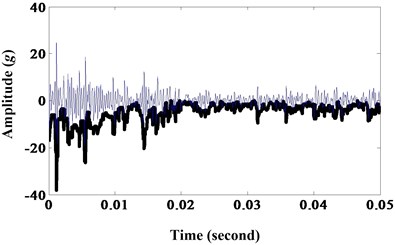
a)
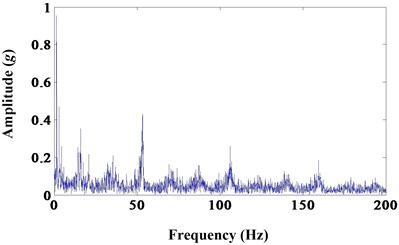
b)
5. Conclusions
This paper deals with the issue of fault diagnosis for planetary gearbox using mathematical morphology analysis. Six morphological filters are used to extract the fault frequencies. It is demonstrated that morphological dilation-erosion gradient filter is better than the other five filters. And planetary gearbox experiment signals are used to validate the conclusion.
References
-
Samuel P. D., Pines D. J. A review of vibration-based techniques for helicopter transmission diagnostics. Journal of Sound and Vibration, Vol. 282, 2005, p. 475-508.
-
Lei Y. G., He Z. J., Lin J., etc. Research advances of fault diagnosis technique for planetary gearboxes. Journal of Mechanical Engineering, Vol. 47, Issue 19, 2011, p. 59-67, (in Chinese).
-
Feng Z. P., Zuo M. J. Vibration signal models for fault diagnosis of planetary gearboxes. Journal of Sound and Vibration, Vol. 331, 2012, p. 4919-4939.
-
Feng Z. P., Zuo M. J. Fault diagnosis of planetary gearboxes via torsional vibration signal analysis. Mechanical Systems and Signal Processing, Vol. 36, 2013, p. 401-421.
-
Samuel P. D., Pines D. J. Vibration separation methodology for planetary gear health monitoring. Proceeding of SPIE, Vol. 3985, 2000, p. 250-260.
-
McFadden P. D. A technique for calculating the time domain averages of the vibration of the individual planet gears and the sun gear in an epicyclic gearbox. Journal of Sound and Vibration, Vol. 144, 1991, p. 163-172.
-
McFadden P. D. Window functions for the calculation of the time domain averages of the vibration of the individual planet gears and sun gear in an epicyclic gearbox. Journal of Vibration and Acoustic, Vol. 116, 1994, p. 179-187.
-
Feng Z. P., Zuo M. J., Chu F. L. Application of regularization dimension to gear damage assessment. Mechanical Systems and Signal Processing, Vol. 24, 2010, p. 1081-1098.
-
Samuel P. D., Pines D. J. Constrained adaptive lifting and the CAL4 metric for helicopter transmission diagnostics. Journal of Sound and Vibration, Vol. 319, 2009, p. 698-718.
-
Fan X. F., Zuo M. J. Gearbox fault detection using Hilbert and wavelet packet transform. Mechanical Systems and Signal Processing, Vol. 20, 2006, p. 966-982.
-
Li B., Zhang P. L., Wang Z. J. etc. Gear fault detection using multi-scale morphological filters. Measurement, Vol. 44, 2011, p. 2078-2089.
-
Morenilla A. J., Carmona R. M., Romero J. L. Mathematical morphology for design and manufacturing. Mathematical and Computer Modelling, Vol. 54, 2011, p. 1753-1759.
