Abstract
The failure of aircraft landing gear (ALG) is major caused by vibration fatigue. And its main failure mode is fatigue fracture. Currently the reliability of ALG is usually calculated by the stress strength interference (SSI) model, which is based on the binary state assumption. While in reality, the strength is degraded with time and the boundary of the failure and success is blur, so the binary state assumption is deviated from the fact. To overcome this problem, this paper uses the membership function (MF) to represent fuzzy safe state which caused by the strength degradation under the failure mode of vibration fatigue. Moreover, a fuzzy reliability model (FRM) of ALG is proposed based on fuzzy failure domain (FFD). Finally, the feasibility of method is tested through a simulation example. By comparing the simulation results (SRs) of the FRM with SRs of the static SSI model and the dynamic SSI model, the rationality of the method is verified. The FRM can calculate the reliability without the gradual degradation processes, thus it is used more widely.
1. Introduction
With the high requirement for safe operation of ALG, the issue of structure reliability under vibration fatigue becomes more and more prominent. ALG is one of the key components of aircraft. Due to the complexity of landing gear structure and nonlinear factors, it is difficult to analysis the reliability of ALG directly from the dynamics. Usually the structure reliability of ALG is calculated by the static SSI model which is widely used in the calculation of structural reliability [1-4]. In this model a certain distribution is used to represent the stress and strength. When the stress suffered by products is greater than the strength, mechanical structure are likely to fail. As a matter of fact, this model is based on the binary state assumption which is deviated from the reality under the vibration fatigue. Because the strength is degraded with time under the vibration fatigue failure mode and the boundary of the failure and success is blur. So the binary state assumption is deviated from the fact. As a result, the reliability estimated by the static SSI model may deviate from the practical situation [4-6].
The failure mode of ALG is fatigue failure which is a depletion process, so the boundaries of safety and failure become blurred. In this case, it is difficult to determine the safety or failure. Therefore, it’s necessary to do the research of the reliability model based on fuzzy reliability under the vibration fatigue. Until now some scholars have done considerable in this field.
For depletion failure, the strength is usually degenerated with stress [7-10]. Gao proposed the dynamic reliability analysis method of degraded mechanical components based on process probability density function of stress [7]. Zhang established reliability calculation model of gears considering strength degradation [10].
Degenerated SSI model solves the problem of strength degradation with stress, but ignores the ambiguity of security status. Hence, it is necessary to combine fuzzy mathematics with reliability during studying structural reliability under the failure mode of vibration fatigue.
In recent years, some efforts have been made to analyze fuzzy reliability of various engineering systems by employing the fuzzy set theory introduced by Zadeh in 1965 [11]. Ma et al. proposed a method to analyze the dynamic response and reliability of fuzzy-random truss systems under the stationary random load [12]. Roberts presented an approach to analyzing fuzzy system reliability by modeling a single fuzzy probability distribution for a component from some possible distributions [13]. Zhou put forward a fuzzy reliability model of pressure piping system considering both the randomness of assessment parameters and the fuzziness of failure areas [14]. Li and Kapur made a lot in the continuous-state reliability measures based on fuzzy sets [15]. Kumar researched the fuzzy system reliability evaluation using time-dependent intuitionistic fuzzy set [16]. Huang proposed a method of reliability assessment for fuzzy multi-state systems [17], and did the reliability analysis of structure for fuzzy safety state [18]. Gao established the fuzzy dynamic reliability model of dependent series mechanical systems [19]. Lv studied the numerical method and fuzzy model for the fuzzy reliability [20, 22].
However, these models mainly focused on static fuzzy reliability analysis of systems. Fuzzy dynamic reliability models of mechanical systems under the vibration fatigue are seldom reported. Besides, when considering the depletion failure of ALG, the existing static fuzzy models cannot be directly extended to fuzzy dynamic reliability models of mechanical systems.
This paper takes the fuzziness of depletion failure under vibration fatigue into account and provides a mathematical tool to deal with the uncertainty involved in reliability models. Due to the limitations of technology and cost, it is difficult or impossible to acquire accurate distribution of stress at each time instant with statistical tools. We transfer the random vibration into a generalized stress. Then use the MF to represent the fuzziness of security status [21]. The MF defines how each element in the fuzzy set is mapped to the degree of membership ranging from 0 to 1, where 1 represents that the corresponding elements completely belong to the fuzzy set, 0 means that the corresponding elements are completely not in the fuzzy set, and values between 1 and 0 represent that the corresponding elements partially belong to the fuzzy set. In this paper, FRM of ALG is established through the FFD. Finally by comparing SRs of the FRM with SRs of the static and dynamic SSI model, the rationality of the method is verified.
2. The fuzzy failure domain’s mathematical description of aircraft landing gear
FFD’s mathematical description of ALG is the model which considers the gradual degradation law of strength under vibration fatigue to the reliability. We assume the generalized strength of ALG is and the generalized stress is S which are two independent data.
The probability density function of generalized strength is .
While the probability density function of Stress is . In addition, the safe state is defined as , and its MF is . Then the mathematical model of FFD can be represented by Eq. (1):
3. Model the fuzzy reliability of aircraft landing gear
The distribution function of generalized strength and generalized stress are , . and are independent.
Fuzzy security state is , its MF is . Then the fuzzy failure rate and fuzzy reliability could be formulated as Eq. (2) and Eq. (3) based on the probability of fuzzy events:
4. Model the fuzzy reliability of aircraft landing gear
Reliability of ALG is calculated by determining the distribution and the parameters in distribution, such as the MF of fuzzy safe state.
4.1. Generalized stress
Due to the limitations of technology and cost, it is difficult or impossible to acquire accurate distribution of stress at each time instant with statistical tools. An alternative method is equivalent the random vibration stress to a generalized stress which is shown in Fig. 1. The above curve in picture a) is one-tenth of the below curve which is the random vibration stress. Fatigue failure is the structure damage in alternating stress which is difficult to direct analysis. Therefore, we equivalent the random vibration to a generalized stress through data processing and analysis and obtain the probability density function which is shown in picture b).
Fig. 1Equivalent diagram of generalized stress
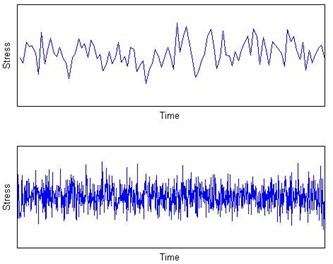
a) Random vibration stress
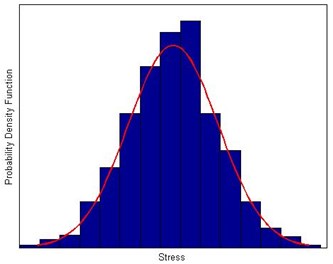
b) Probability density function
4.2. Selecting of membership function
The failure mode of ALG is fatigue failure which is depletion-type failure. In its interference area, the stress suffered by products is greater than the strength and mechanical structure are likely to fail. What’s more, the failure rate increases with the increase of the difference between generalized strength and generalized stress which are shown in Fig. 2. b) is the picture which enlarge the box in a).
Fig. 2The interferogram of generalized strength and generalized stress
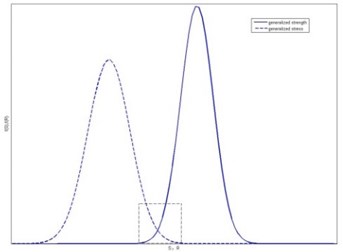
a)
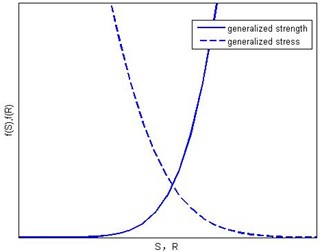
b)
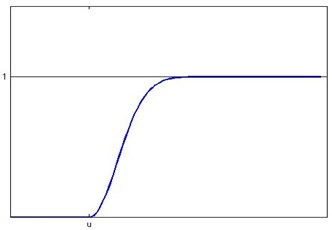
Accordingly, in this paper, the partial large normal distribution membership function is adopted to describe the fuzzy characteristics of safe state in the fuzzy reliability calculation.
MF of the fuzzy safe state is:
where , .
Fig. 3Membership function of partial large Normal distribution
4.3. Calculation of the fuzzy reliability model
Based on the selecting of membership function and the parameters, the failure rate of ALG can be calculated by Eq. (5) from the Eq. (2), to (4):
Let be:
Then:
The reliability is:
The calculation of FFD M is familiar to the failure rate. The reliability also can be calculated directly from the Eq. (3) to (5).
5. Numerical example
The strength of ALG obeys the normal distribution which average value and variance are 630 MPa and 44.1. The average value and variance of the external stress are 750 MPa and 37.5. The generalized stress and generalized strength interference cure is shown in Fig. 5.
SRs shown in Table 1.
Fig. 5SSI Graph of ALG
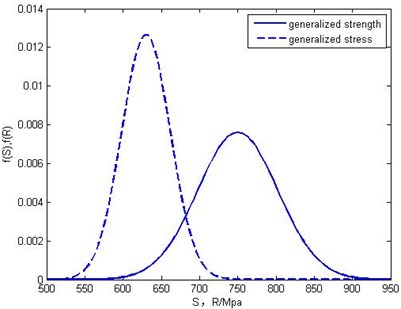
Table 1Result of fuzzy reliability model
Reliability index | Fuzzy failure domain | Failure rate | Reliability |
Simulation result | 0.9342 | 0.0393 | 0.9607 |
6. Conclusions
By transferring the random vibration stress to a normal distribution and taking the fuzziness of safe state into consideration, this paper established the FRM of ALG based on the static SSI model. Finally two conclusions are drawn at the end of the dissertation:
1) In this paper, MF in fuzzy mathematics illustrates the fuzzy failure state of ALG during the calculation. Furthermore, fuzzy reliability model is established by vibration fatigue failure mode without knowing the law of strength degradation. Accordingly, when strength degradation law does not known, this model has stronger applicability. So it’s a method that can be widely used.
2) This fuzzy reliability model can be extended to other situation, for example, the distribution of strength and stress that obeys the exponential distribution, Weibull distribution or Log-normal distribution. Furthermore, for the situation of random stress – fuzzy strength and fuzzy stress –random strength, the fuzzy model also works.
References
-
Li Y., Chen J., Liu J., et al. Estimation of the reliability of all-ceramic crowns using finite element models and the stress-strength interference theory. Computers in Biology and Medicine, Vol. 43, Issue 9, 2013, p. 1214-1220.
-
Huang Z., Jin Y. Extension of stress and strength interference theory for conceptual design-for-reliability. Journal of Mechanical Design, Vol. 131, Issue 7, 2009, p. 1-12.
-
Wang X. G., Zhang Y. M., Wang B. Y. The inf1uence of the frequency of loading and stress degradation on SSI model. Machinery Design and Manufacture, Vol. 12, Issue 12, 2008, p. 205-207.
-
An Z. W., Huang H. Z., Liu Y. A discrete stress – strength interference model based on universal generating function. Reliability Engineering and System Safety, Vol. 93, Issue 10, 2008, p. 1485-1490.
-
Wang Z., Li Y., Huang H. Z., et al. Reliability analysis of structure for fuzzy safety state. Intelligent Automation and Soft Computing, Vol. 18, Issue 3, 2012, p. 215-224.
-
Xian L. Y., Zhu J. Y., Hao C. Z. System level load-strength interference based reliability modeling of k-out-of-n system. Reliability engineering and system safety, Vol. 84, Issue 3, 2004, p. 311-317.
-
Gao P., Xie L. Dynamic reliability analysis method of degraded mechanical components based on process probability density function of stress. Mathematical Problems in Engineering, 2014, p. 1-12.
-
Brissaud F., Smidts C., Barros A., et al. Dynamic reliability of digital-based transmitters. Reliability Engineering and System Safety, Vol. 96, Issue 7, 2011, p. 793-813.
-
Wong C. N., Huang H. Z., Xiong J. Q., et al. Weibull distributed stress-dependent strength analysis of AE. Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Montreal, Quebec, Canada, 2010.
-
Lv Sh. Z., Liu H. N., Zhang D. W., et al. Reliability calculation model of gears considering strength degradation. Industrial Engineering and Engineering Management International conference, Beijing, China, 2009.
-
Zadeh L. A. Fuzzy sets. Information and Control, Vol. 8, Issue 3, 1965, p. 338-353.
-
Ma J., Gao W., Wriggers P., Wu T., Sahraee S. The analyses of dynamic response and reliability of fuzzy-random truss under stationary stochastic excitation. Computational Mechanics, Vol. 45, Issue 5, 2010, p. 443-455.
-
Roberts I. D., Samue A. E. The use of imprecise component reliability distributions in reliability calculations. IEEE Transactions on Reliability, Vol. 45, Issue 1, 1996, p. 141-144.
-
Zhou J. Reliability assessment method for pressure piping containing circumferential defects based on fuzzy probability. International Journal of Pressure Vessels and Piping, Vol. 82, Issue 9, 2005, p. 669-678.
-
Li Z., Kapur K. C. Continuous-state reliability measures based on fuzzy sets. IIE Transactions, Vol. 44, Issue 11, 2012, p. 1033-1044.
-
Kumar M., Prasad Yadav S., and Kumar S. Fuzzy system reliability evaluation using time-dependent intuitionistic fuzzy set. International Journal of Systems Science, Vol. 44, Issue 1, 2013, p. 50-66.
-
Liu Y., Huang H. Z. Reliability assessment for fuzzy multi-state systems. International Journal of Systems Science, Vol. 41, Issue 4, 2010, p. 365-379.
-
Wang Z., Li Y., Huang H. Z., Liu Y. Reliability analysis of structure for fuzzy safety state. Intelligent Automation and Soft Computing, Vol. 18, Issue 3, 2012, p. 215-224.
-
Gao P., Yan S. Fuzzy dynamic reliability model of dependent series mechanical systems. Advances in Mechanical Engineering, Vol. 23, Issue 2, 2013, p. 1-15.
-
Tang Z., Lu Z., Xia Y. Numerical method for fuzzy reliability analysis. Journal of Aircraft, Vol. 50, Issue 6, 2013, p. 1710-1715.
-
Liu Y., Li Y. Dynamic modeling and adaptive neural-fuzzy control for nonholonomic mobile manipulators moving on a slope. International Journal of Control, Automation and Systems, Vol. 44, Issue 2, 2006, p. 197-203.
-
Lu Z. ZH. Unified model of fuzzy and random reliability analysis. Acta Mechanica Sinica, Vol. 36, Issue 5, 2004, p. 533-539.
