Mid-frequency prediction of transmission loss using a novel hybrid deterministic and statistical method

Wu, Fei; Liu, Gui Rong; Li, Guangyao; Cheng, Aiguo; He, Zhicheng

Vibroengineering Procedia

Browse Procedia

Published: 03 November 2014

Check for updates

Mid-frequency prediction of transmission loss using a novel hybrid deterministic and statistical method

Fei Wu¹

Gui Rong Liu²

Guangyao Li³

Aiguo Cheng⁴

Zhicheng He⁵

^{1, 3, 4, 5}Key Lab of Advanced Technology for Vehicle Body Design and Manufacture, Hunan University, Changsha, 410082, P. R. China

²Department of Aerospace Engineering and Engineering Mechanics, University of Cincinnati 2851 Woodside Dr, Cincinnati, OH 45221, USA

Corresponding Author:

Fei Wu

Cite the article Download PDF

Downloads 1299

Abstract

A novel hybrid deterministic-statistical approach named ES-FE-SEA method specially used to predict the sound Transmission loss of panels in mid-frequency is proposed in this paper. The proposed hybrid methods takes the best advantages of edged-based smoothing FEM (ES-FEM) and statistical energy analysis (SEA) to further improve the accuracy of mid-frequency transmission loss predictions. The application of ES-FEM will “soften” the well-known “overly-stiff” behavior in the standard FEM solution and reduce the inherent numerical dispersion error. While the SEA approach will deal with the physical uncertainty in the relatively higher frequency range. Two different types of subsystems will be coupled based on “reciprocity relationship” theorem. The proposed was firstly applied to a standard simple numerical example, and excellent agreement with reference results was achieved. Thus the method is then applied to a more complicated model-a 2D dash panel in a car. The proposed ES-FE-SEA is verified by various numerical examples.

1. Introduction

The predictions of sound Transmission loss in mid-frequency regime have been one of hotspots and difficulties in academy and engineering. There are many contributed efforts to improve the modeling techniques to solve such transmission loss problems. Some variational approaches [1] and wave approaches [2] attempted to solve the transmission loss based on the exact analytical solutions. Because of the basic simplifications and assumptions, these approaches, however, are only suitable for special cases and provide just rough estimates. Numerical modeling approaches such as the finite element method (FEM) [3] can be applied without restrictions for different geometries of cavities and plates but often have limited applicability to mid and high frequency range responses. The statistical energy analysis (SEA) [4] is another possible approach for solving the transmission loss problems. SEA approach can deal with high frequency transmission loss problems, but often cannot be applied in the lower frequency range All in all there are still a lot of problems to calculate the transmission loss using the above-mentioned approaches.

When the frequency of interest shifted to the mid-frequency domain, the airborne sound transmission prediction through a panel become more difficult. The mid-frequency response of transmission loss systems often exhibit the mixed behaviors (either deterministic or statistic behaviors) [5]. A single deterministic method like FEM or statistic method as SEA can hardly solve mid-frequency transmission loss problem properly. Recently, the hybrid FE-SEA developed by Robin S. Langley becomes the mainstream method meant for mid-frequency problems [6]. However, the use of conventional FEM in conventional hybrid methods entails some inherent drawbacks, which are closely related to the well-known “overly-stiff” feature of FEM and its sensitivity to numerical pollution errors [7, 8]. In this paper, a novel hybrid edge-based smoothed FEM coupled with statistical energy analysis (ES-FE-SEA) method is proposed, and can in principle handle all these restrictions lies in a single deterministic or statistical method and conventional hybrid methods. The edge-based smoothed technique will help to extend the application of conventional FEM to mid-frequency with higher accuracy and efficiency while SEA will deal with all the uncertainty in the transmission system. The embedding of the ES-FEM in hybrid ES-FE-SEA framework presents a promising combination for solving mid-frequency transmission loss problems. This is also the essential motivation of this work.

2. Theory summary

The hybrid ES-FE-SEA takes the best advantages of two well established techniques: SEA and ES-FEM. These two methods are briefly reviewed in the following.

2.1. The basic formulations of ES-FEM

In the conventional FEM, the calculation of stiffness matrix can be written as follows [9]:

1

K = \int_{Ω}^{} B_{b}^{T} D_{b} B_{b} d Ω + \int_{Ω}^{} B_{s}^{T} D_{s} B_{s} d Ω,

in which $B_{b}$ and $B_{s}$ are strain-deflection matrix for bending and shearing, respectively. $D_{b}$ is the bending stiffness constitutive coefficients, and $D_{s}$ is transverse shear stiffness constitutive.

In ES-FEM, strains calculation is based on the edge-based smoothed domain rather than the 3-node triangles element domain. The smoothing operation is firstly applied to the bending (in-plane) strain and the shear (off-plane) stain of the plate over each of the edge-based smoothing domains:

2

{\bar{B}}_{b i} (x_{k}) = \frac{1}{A_{k}} \sum_{i = 1}^{N_{k}^{e}} \frac{1}{3} A_{e}^{i} B_{b i} (x_{k}), {\bar{B}}_{s i} (x_{k}) = \frac{1}{A_{k}} \sum_{i = 1}^{N_{k}^{e}} \frac{1}{3} A_{e}^{i} B_{s i} (x_{k}),

in which $N_{k}^{e}$ is the number of the sub-domain of edge $k$ and $A_{e}^{i}$ is the area of $i$ th sub-domain in a triangle element. $A_{k}$ is the area of the smoothing domain $Ω_{k}$ , which can be calculated as follows:

3

A_{k} = \int_{Ω_{k}}^{} d Ω = \frac{1}{3} \sum_{i = 1}^{N_{k}^{e}} A_{e}^{i} .

Using the smoothed strain matrix ${\bar{B}}_{s}$ and ${\bar{B}}_{b}$ to replace $B_{s}$ and $B_{b}$ , the smoothed stiffness matrix $\bar{K}$ based on the smoothing domain can be evaluated as:

4

\bar{K} = \sum_{k = 1}^{N_{s}} A_{k} {\bar{B}}_{b}^{T} D_{b} {\bar{B}}_{b} + \sum_{k = 1}^{N_{s}} A_{k} {\bar{B}}_{s}^{T} D_{s} {\bar{B}}_{s} .

Finally the edged-based discretized system equations for Reissner-Minlin plate elements can be re-written as:

5

M \ddot{u} + \bar{K} u = F,

where $M$ is the mass matrix, $u$ is total unknown variables, $F$ is referred as vector of nodal forces.

2.2. The basic formulations of SEA

The Statistical Energy Analysis (SEA) calculation is based on the principle of conservation of energy which flows in and out of a subsystem. Only one single degree of freedom (energy of vibration), rather than potentially thousands of degrees of freedom in FEM, is needed to describe the vibrational behavior of a subsystem. Therefore, this approach can dramatically save great computational time through reducing the numerical model size. The power balance equations for two subsystems can be written in a matrix form as below:

6

[\begin{array}{l} P_{i} \\ P_{j} \end{array}] = ω [\begin{matrix} (η_{i d} + η_{i j}) & - η_{j i} \\ - η_{i j} & (η_{j d} + η_{j i}) \end{matrix}] [\begin{array}{l} E_{i} \\ E_{j} \end{array}],

where $P_{i}$ and $P_{j}$ are the external source excitations which are applied directly to the subsystem. $η_{i j}$ and $η_{j i}$ are the coupling loss factors of two subsystems. $ω$ is the angular frequency. $η_{i d}$ and $η_{j d}$ are the damping loss factors. $E_{i}$ and $E_{j}$ are the average vibrational energy of two subsystems. The power balance equations can be easily extend to the a big system with $n$ numbers of subsystems. Detailed principles of statistical energy analysis (SEA) can refer to Ref. [4].

3. The hybrid ES-FEM/SEA equations

The coupling of an ES-FEM subsystem and two SEA subsystems is described based on the “reciprocity relationship” theorem. According to the diffuse field reciprocity relation, the cross-spectrum of the forces on the boundary of a statistical subsystem can be written in terms of subsystem vibrational energy as follow:

7

〈S_{f f}^{r e v}〉 = \frac{4 E}{π ω n} I m \{D_{d i r}\},

where $D_{d i r}$ is the direct field dynamic stiffness matrix related to an acoustic half-space on one side of the infinite planar baffle. The dynamic stiffness matrix can be calculated using the approach of Jinc functions based on some grid of points embedded in the infinite planar baffle [10]. The statistical cavity subsystem is discomposed into “direct field” and “reverberant field”. For each subsystem, power balance condition leads to the following set of additional equations:

8

P_{i n} = p_{o u t}^{r e v} + p_{d i s s},

where $P_{i n}$ is the input power that is assumed to be characterized and known. $p_{o u t}^{r e v}$ is the power leaving the reverberant field. $p_{d i s s}$ is the dissipated power that is assumed to be proportional to damping. Full details of the derivation of the above equations can be found in Ref. [6].

We assume that the left cavity is the acoustic source cavity and carries a input power $P_{1}$ . The transmitted power $P_{3}$ of the right cavity can be obtained using Hybrid ES-FE-SEA equations. The transmission loss of the plate is defined as [11]:

9

T L = 10 l o g_{10} (\frac{P_{1}^{2}}{P_{3}^{2}}) - 10 l o g_{10} [\frac{A}{(S_{3} a_{3})}],

where $A$ is the area of the panel and $S_{3}$ and $a_{3}$ are the surface area and absorption coefficient of the right hand room, respectively.

4. Numerical application of the hybrid ES-FE-SEA

4.1. Validation of ES-FEM/SEA

In order to validate the proposed ES-FE-SEA, a standard numerical example for benchmarking is examined, which was original studied by Robin S. Langley using hybrid FE-SEA [6]. The thickness of panel is 0.015 m. The hybrid FE-SEA model and FEM model shows as following Fig. 1.

Fig. 1Sketch of a transmission loss system

a) Hybrid FE-SEA (VA-One)

b) FEM model

The convergence study of the proposed hybrid ES-FE-SEA is first carried on a very fine mesh with 3,598 triangle elements and 1,884 nodes. The reference results are obtained by VA-One software using the embedded hybrid FE-SEA also based on that fine mesh. The simply supported boundary conditions around the plate perimeter are chosen to compare the results. Coupling loss factors of two cavities and transmission loss factor of the plate are plotted in Fig. 2.

Fig. 2The validation of the ES-FE-SEA

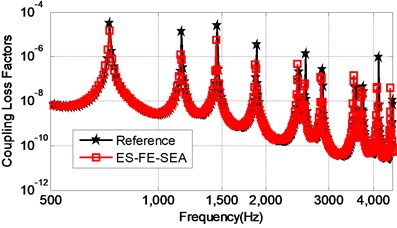
a) Coupling loss factor of two cavities

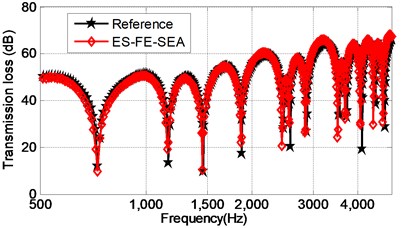
b) The transmission loss factor of the free plate

Fig. 3The comparison between the ES-FE-SEA and conventional FE-SEA

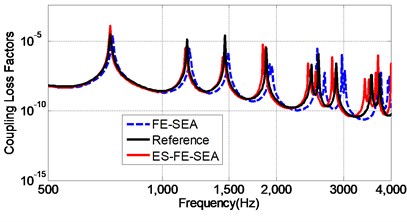
a) Coupling loss factor of two cavities

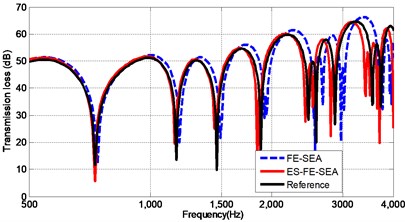
b) The transmission loss factor of the free plate

The results obtained from ES-FE-SEA show excellent agreements with the reference result. Therefore, the validation and effectiveness of the present method is confirmed in this example. In order to compare the accuracy of ES-FE-SEA and conventional FE-SEA, the proposed method is applied to a rough mesh with 244 triangle elements with 143 nodes. The reference result is obtained on VA-ONE software by using FE-SEA with a very fine mesh (5,908 triangle elements and 3050 nodes). The results obtained by different methods are plotted in Fig. 3.

As shown in the Fig. 3, it is obvious that ES-FE-SEA provides a higher accuracy results compared with the FE-SEA in the whole low to mid-frequency regime. Even applied in the model with much less DOFs (244 DOFs), ES-FE-SEA is still able to provide the result in almost the same accuracy level as the result of FE-SEA using fine mesh (5,908 DOFs). To sum up, the high accuracy and computational efficiency of ES-FEM/SEA for mid-frequency solution is illustrated in this example.

4.2. Dash panel model

In this part, a transmission loss model of complicated dash panel is established using the hybrid ES-FE-SEA as illustrated schematically in Fig. 4. The hybrid model consists of two adjacent reverberation cavities and dash panel of interest. Two adjacent reverberation cavity are simply extracted by the dash panel with the volume of 1.5 m³. The material parameters of dash panel are given as: the density $ρ =$ 7800 kg/m³, Yong’s modulus $E =$ 210 GPa and Poisson’s ratio $ν =$ 0.3. The dash panel has the thickness of 15 mm.

Fig. 4A transmission loss model of dash panel

a) Hybrid FE-SEA (VA-One)

b) FEM model

The dash panel compartment is first divided using 260 triangle elements with 160 nodes for ES-FEM or FEM. The results are compared against the reference result that is calculated by VA-ONE software using coupled FE-SEA model, where the dash panel is divided with 1,842 triangle elements and 1,012 nodes. The transmission loss factor of the dash panel is calculated using different methods as shown in Fig. 5. The analysis frequency range was between 0-2000 Hz.

Fig. 5The transmission loss factor of the front windshield

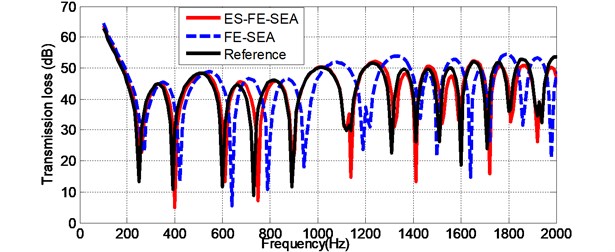
The results for this complicated vehicle example re-enforces the finding from the example for benchmarking. In the whole mid-frequency domain, the ES-FEM/SEA constantly provides much more accurate result in higher frequency range, compared with the FE-SEA model using the same mesh. Thus, the method could be used for the more complicated model.

5. Conclusions

This paper investigated the transmission loss of a simple panel and complicated dash panel using the newly developed hybrid ES-FE-SEA method in mid-frequencies. Compared with conventional FE-SEA, the proposed ES-FE-SEA approach takes the best advantages of edged-based smoothing techniques to “soften” the stiffness of the deterministic subsystem, thus eliminating the numerical error in standard FEM. Therefore, the ES-FE-SEA constantly provides much more accurate result in the mid to high frequency range, comparing with the FE-SEA model based on the same mesh.

References

Gagliardini L., Roland J., Guyader J. L. The use of a functional basis to calculate acoustic transmission between rooms. Journal of Sound and Vibration, Vol. 145, Issue 3, 1991, p. 457-478.

Search CrossRef
Nilsson A. C. Reduction index and boundary conditions for a wall between two rectangular rooms. Part I: Theoretical results. Acta Acustica united with Acustica, Vol. 26, Issue 1, 1972, p. 1-18.

Search CrossRef
Sakumaa Tetsuya, Kenichi Egawab, Yosuke Yasudac Numerical analysis of sound transmission loss of glass pane – on the treatment of edge damping. Moment, Vol. 500, 2008.

Search CrossRef
Crocker M. J., A. J. Price sound transmission using statistical energy analysis. Journal of Sound and Vibration, Vol. 9, Issue 3, 1969, p. 469-486.

Search CrossRef
Ladeveze P., et al. A multiscale computational method for medium-frequency vibrations of assemblies of heterogeneous plates. Computers and Structures, Vol. 81, Issue 12, 2003, p. 1267-1276.

Search CrossRef
Shorter Phil J., Langley R. S. Vibro-acoustic analysis of complex systems. Journal of Sound and Vibration, Vol. 288, Issue 3, 2005, p. 669-699.

Search CrossRef
Liu G. R., Dai K. Y., Nguyen T. T. A smoothed finite element method for mechanics problems. Computational Mechanics, Vol. 39, Issue 6, 2007, p. 859-877.

Search CrossRef
Wu F., Liu G. R., Li G. Y., Cheng A. G., He Z. C. A new hybrid smoothed FEM for static and free vibration analyses of Reissner-Mindlin Plates. Computational Mechanics, 2014, p. 1-26.

Search CrossRef
Liu G. R. Meshfree Methods: Moving Beyond the Finite Element Method. 2nd ed., CRC Press, 2009.

Search CrossRef
Langley R. S. Numerical evaluation of the acoustic radiation from planar structures with general baffle conditions using wavelets. The Journal of the Acoustical Society of America, Vol. 121, Issue 2, 2007, p. 766-777.

Search CrossRef
Bies David A., Hansen Colin H. Engineering Noise Control: Theory and Practice. CRC Press, 2009.

Search CrossRef

About this article

Received

Accepted

15 July 2014

Published

03 November 2014

Keywords

transmission loss

edge-based smoothed finite element (ES-FEM)

ES-FE-SEA

mid-frequency

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.