Abstract
Gear rattle in a quick-return mechanism is studied. Rattling is characterized by experimental work in a mechanical system with two gears driven by an electric motor. The acceleration of the mechanical vibrations and the variations in the electrical current of the motor were measured by means of sensors connected to a data acquisition system. The results obtained are presented in time-domain plots, and analyzed in the frequency domain by power spectra. It is shown that rattling is well identified in the time-domain plots for both parameters, while it is only evident in the motor electrical current signal in the frequency-domain analyses.
1. Introduction
Quick return (QR) mechanisms can be found in numerous industrial applications [1]. A QR mechanism is one which has a slower working stroke and a quick-return stroke. It has a time ratio (TR) defined as the ratio of the change in input displacement during the working stroke to its change during the return stroke, and several basic types of mechanisms have this QR action [2].
Gears are commonly found in QR mechanisms and mesh stiffness and backlash between the teeth play an important role in the dynamics of a gear system. Its vibration response depends on the applied forces, which may show a complex behavior. Meshing faults may appear due to wear during operation or incorrect production tolerances. The system is also sensitive to errors in the distance between teeth, that in conjunction with the time varying mesh stiffness exhibits a nonlinear oscillator response [3]. This response produces gear rattle, which is influenced by the interaction between eccentricity and the external forcing fluctuation.
The small gap between the trailing face of one tooth and the leading face of the next is known as backlash, and it is needed to ensure that gears do not jam. Gears may lose contact under lightly damped operation, which arises when there is no torque transfer between them. Consequently, an oscillatory force excites modes where gears rattle by repeatedly loosing and re-establishing contact [4]. Other factors influencing the dynamics of the system include eccentricity, which may be introduced by misalignment, imperfections in grub screw tightness or ill-fitting bearing. This interaction produces large variations in backlash oscillation amplitudes [5].
Revolute joints with clearance are commonly found in these mechanical systems, and they also produce a contact-impact phenomenon due to the sudden changes in the velocity of the QR mechanism [6]. Experiments with extremely accurate gears and small tooth errors have demonstrated that even under these conditions, phase changes of the external force affect the relative forcing between the gears and therefore the amplitude of gear rattle. Small perturbations present in real systems can also have large effects on the system response [7].
A common example of rattling is the neutral rattle noise that gearboxes in vehicles generate by gear impacts in non-engaged gear pairs [8]. The cause is the torsional vibration of transmission components that are not under load, and can be minimized by optimizing transmission parameters such as backlash, axial clearance and main centre distance [9]. Experimental studies have been carried out to describe the rattle phenomenon under multi harmonic excitation [10]. Extended methodologies have also been developed which consider not only the torsional vibrations, but the hydrodynamic contact film due to lubricants, formed between gear teeth under light impact loads. This film behaves like a nonlinear spring damper which affects the response of idle gears during the meshing cycle. The system is strongly affected by lubricant properties, and viscosity is one of the main factors governing the overall system behavior, affecting drag torque, friction and inertia of the idle gears, promoting rattle [11, 12].
Additionally, in QR mechanisms the dynamic behavior of the system is also influenced by the geared rotor and mechanical coupling effects. It has been found that in a rod-crank linkage, longer cranks, small bearing stiffness and shaft radius induce larger rod deflections, while the bearing damping can suppress the rod oscillations. High frequency oscillations are also produced by the transmission error of gear mesh [13].
2. Experimental setup
A quick return mechanism was built to study mechanical vibrations produced under rattling conditions. Fig. 1 shows the simplified schematic of the system. A gear set was used, where a servomotor drives a pinion or secondary gear (G1), while a main gear (G2) drives a slotted bar (2) by means of a driving pin (3). Rigid linkages (1) (2) are used to transfer a linear motion to a ram.
Fig. 1Schematic diagram of the experimental quick return mechanism
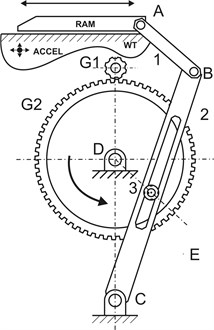
Mechanical vibrations in the directions of the ram displacement and normal to the floor were measured and recorded with a biaxial accelerometer. A phase signal detector to identify the beginning of each working cycle of the mechanism was implemented with a proximity transducer. A level change in the output signal of this sensor was obtained in presence of the ram, as a reference point for the cycle. The motor current was also measured by means of an analog signal output of the controller. A measurement system for recording the analog signals was implemented with a NI USB-6251 DAQ and a LabVIEW program. The pinion gear was composed of 11 teeth and the main gear of 67 teeth. Experiments were carried out with the motor operating at a speed of 600 rpm and data was acquired at a sampling rate of 10 kHz.
3. Analysis and discussion of results
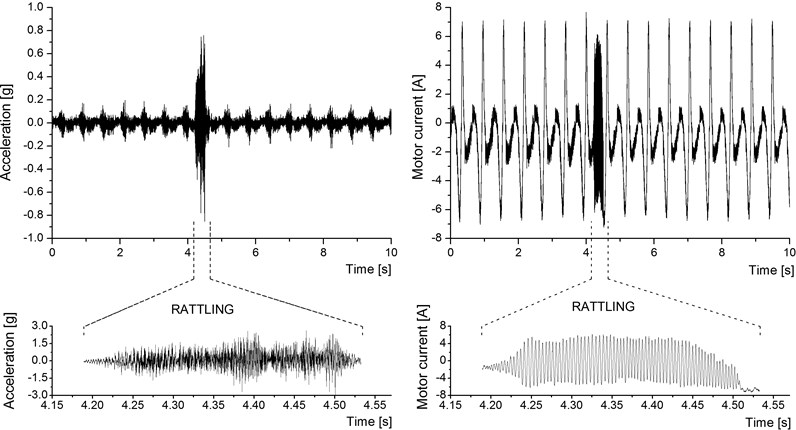
Temporal characteristics of the signals obtained with the QR mechanism are depicted in Fig. 2. It shows the time-domain rattling occurrence, located at the middle of the data record. The working cycle can be identified by the main oscillation in the motor electrical current. Rattling has been expanded in the lower plots, and the motor current variation, when the phenomenon occurs, is characterized by a more regular pattern than that of the acceleration signal.
With respect to the acceleration graph, a repetitive increase in the amplitude of the signal characterizes the quick return stroke, and the rattling reaches a noticeable major acceleration level. A strong variation in the amplitude of accelerometer signal can also be noticed in the expanded plot. On the other hand, the motor current signal shows two repetitive patterns. The lower-amplitude signal pattern corresponds to the slower stroke, while the sharp higher-amplitude signal pattern corresponds to the quick return stroke. In contrast to the acceleration, the current expanded graph shows a signal with sustained amplitude for the motor current when rattling occurs. Both signals show the shorter time that characterizes the return stroke of the mechanism.
Fig. 2Rattling signals in the acceleration and current records
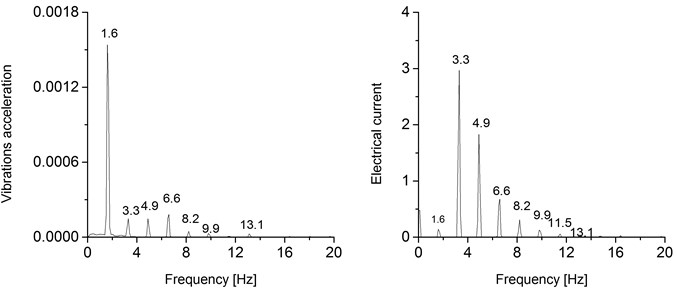
Acceleration and current signals were analyzed in the frequency domain. The lower portion of the power spectrum is shown in Fig. 3. A main frequency can be identified in the acceleration spectrum, located at 1.6 Hz, with various harmonics of much lower amplitude. According to the experimental conditions, running the motor at 600 rpm over a pinion with 11 teeth and applied to a main gear with 67 teeth, will produce a mechanism working frequency of 1.64 Hz, which is in concordance with the measured signals and the spectrum obtained. On the other hand, the electrical current is characterized by a spectrum rich in harmonics with the main frequency located at 3.3 Hz. This is due to the motor load peaks, which occur twice during one working cycle as can be observed in Fig. 2.
Fig. 3Lower portion of the power spectrum of the signals
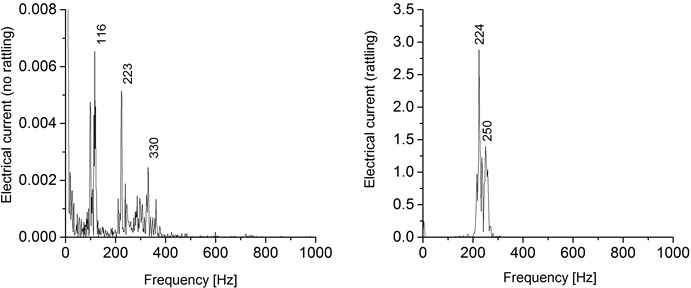
A detailed comparative analysis of electrical current power spectra for rattling occurrence is shown in Fig. 4. For this parameter, when rattling is not present, there is a well-defined peak at 116 Hz, which corresponds to the variations in electrical current produced by the applied torque of the pinion teeth driving the main gear at 600 rpm. Theoretically, a fundamental frequency was expected at 110 Hz, which in practice seems to be translated by the mixture of the motor control variations and the complexity of the mechanical system response. Two other harmonics at 116 Hz and 223 Hz, are also present in the signal. When rattling is isolated, as it is the case in the right-hand graph, the signal is characterized by a fundamental frequency located at 224 Hz. A cleaner spectrum is observed since the electrical current variations show a more regular pattern as it was shown in Fig. 2. The doubling effect over the no-rattling main frequency is evidence of the oscillatory phenomenon produced by the rattling of the gears. This is consistent with work developed by other authors, where it is reported that rattle occurs at frequencies closed to the harmonics of the driving speed [7].
Fig. 4Motor electrical current power spectra for rattling and no-rattling conditions
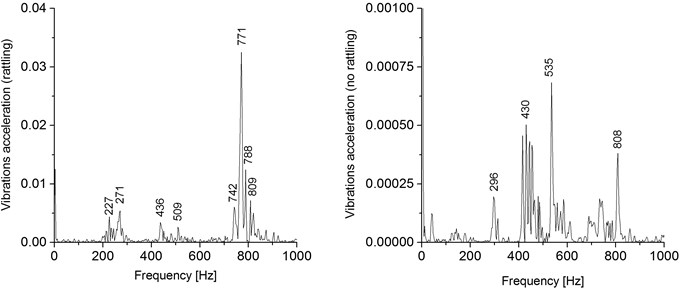
The mechanical behavior of the system, measured through the vibrations acceleration of the physical structure is shown in Fig. 5. It is characterized by main frequencies located at positions other than those found in the electrical current variations. When rattling is present, the structure of the mechanism is excited with a main frequency of 771 Hz, which may correspond to the natural frequency of the mechanical framework, although a trace of the driving excitation can be observed at 227 Hz. When there is no rattling, the mechanical vibrations produce a power spectrum rich in frequencies of low amplitude.
Fig. 5Vibrations acceleration power spectra for rattling and no-rattling conditions
4. Conclusions
The rattling phenomenon in a quick return mechanism has been characterized through the analysis of the mechanical vibrations of the framework system and the current variations of the excitation motor. The vibrations acceleration amplitude grow considerable when the mechanism rattles, while the motor current shows variations characterized by a sustained peak-to-peak amplitude during the event. A frequency analysis of the signals was made and it was observed that the rattling frequency is well localized in the motor current spectrum, while the pinion excited frequencies are also identified under rattle absence conditions. The mechanical vibrations, described through the aceleration parameter, shows a spectra rich in various frequencies excited by the structural elements of the mechanical system. Rattling and excitation frequencies derived from the motor and gears are not as evident in the acceleration signal as in the motor electrical current spectra.
References
-
Beale D. G., Scott R. A. The stability and response of a flexible rod in a quick return mechanism. Journal of Sound and Vibration, Vol. 141, 1990, p. 277-289.
-
Podhorodeski R. P., Nokleby S. B., Wittchen J. D. Quick-return mechanism design and analysis projects. International Journal of Mechanical Engineering Education, Vol. 32, 2004, p. 100-114.
-
Litak G., Friswell M. I. Dynamics of a gear system with faults in meshing stiffness. Nonlinear Dynamics, Vol. 41, 2005, p. 415-421.
-
Halse C. K., Wilson R. E., di Bernardo M., Homer M. E. Coexisting solutions and bifurcations in mechanical oscillators with backlash. Journal of Sound and Vibration, Vol. 305, 2007, p. 854-885.
-
Ottewill J. R., Neild S. A., Wilson R. E. Intermittent gear rattle due to interactions between forcing and manufacturing errors. Journal of Sound and Vibration, Vol. 321, 2009, p. 913-935.
-
Flores P., Ambrósio J. On the contact detection for contact-impact analysis in multibody systems. Multidoby System Dynamics, Vol. 24, 2010, p. 103-122.
-
Ottewill J. R., Neild S. A., Wilson R. E. An investigation into the effect of tooth profile errors on gear rattle. Journal of Sound and Vibration, Vol. 329, 2010, p. 3495-3506.
-
Dion J. L., Le Moyne S., Chevallier G., Sebbah H. Gear impacts and idle gear noise: Experimental study and non-linear dynamic model. Mechanical Systems and Signal Processing, Vol. 23, 2009, p. 2608-2628.
-
Dogan S. N. Loose part vibration in vehicle transmissions – gear rattle. Turkish Journal of Engineering and Environmental Science, Vol. 23, 1999, p. 439-454.
-
Barthod M., Hayne B., Tébec J. L., Pin J. C. Experimental study of dynamic and noise produced by gearing excited by multi-harmonic excitation. Applied Acoustics, Vol. 68, 2007, p. 982-1002.
-
Tangasawi O., Theodossiades S., Rahnejat H. Lightly loaded lubricated impacts: Idle gear rattle. Journal of Sound and Vibration, Vol. 308, 2007, p. 418-430.
-
Theodossiades S., Tangasawi O., Rahnejat H. Gear teeth impacts in hydrodynamic conjunctions promoting idle gear rattle. Journal of Sound and Vibration, Vol. 303, 2007, p. 632-658.
-
Chang J. R. Coupling effect of flexible geared rotor on quick-return mechanism undergoing three dimensional vibration. Journal of Sound and Vibration, Vol. 300, 2007, p. 139-159.
