Abstract
In this paper a revised averaging method is presented, that does not need the detuning factor in the solving procedure. Comparison with the traditional averaging method shows that it has the similar solving procedure and the same result as the primary resonance of the traditional averaging method. Then the nonlinear oscillator with only polynomial-type displacement nonlinearity is studied, and the general forms of the first-order approximate solution by this revised averaging method, and by the traditional averaging method for the super-harmonic resonance and sub-harmonic resonance are established. At last, the Duffing oscillator is investigated as an example, and the comparison of the analytical and numerical results proves the validity and simplicity of the presented method.
1. Introduction
Averaging method is an effective analytical method for the approximate solution of the weakly nonlinear system. Since its presentation [1, 2], averaging method had been revised and improved to process a lot of nonlinear problems, and some relevant advances were summarized in the monographs [1-4].
Averaging method has been applied in a great deal theoretic and engineering problems extensively [5-13]. For example, Wang and Hu [5] reduced the delay differential equation of infinite dimensional to an ordinary differential equation by averaging method. Roy [6] developed the averaging method to find the periodic solutions of strongly nonlinear oscillators with harmonic excitations. Chatterjee [7] improved the averaging method based on harmonic balance, where the closed form solutions to the unperturbed problem were not needed, so as to research some strongly nonlinear system. Kumar and Datta [8] used the stochastic averaging technique to research the probability density function of the response for strongly nonlinear system subject to both multiplicative and additive random excitations. Ji and Hansen [9] constructed a valid asymptotic expansion solution of a nonlinear oscillator composed of a weakly nonlinear and a linear differential equation based on the averaging method and the continuity condition. Then they [10] extended this strategy to an approximate solution for the super-harmonic resonance of a periodically excited nonlinear oscillator with a piecewise nonlinearity, and the validity of the developed analysis was confirmed by comparing the approximate solutions with the results of direct numerical integration of the original equation. Yang, Tang, Chen and Lim [11] applied the averaging method to analyze the instability phenomena caused by sub-harmonic and combination resonance of transverse parametric vibrations of an axially accelerating tensioned Timoshenko beam on simple supports. Li, Ji and Hansen [12] studied a system composed of two Van der Pol oscillators with delayed position and velocity coupling by the averaging method, where the stability and the number of periodic solutions in 1:1 internal resonance were researched. Yang and Chen [13] investigated the parametrical vibration of a nonlinear oscillator with Davidenkov’s hysteretic nonlinearity by the averaging method and singularity theory, and the universal unfolding was also obtained.
In the above researches, the averaging method were generally used to obtain the approximate solution according to the relationship between the excitation frequency and the natural frequency, so as to induce different responses, such as the primary resonance, sub-harmonic resonance and super-harmonic resonance, etc. In this paper, we revise the traditional averaging method, and find that the revised averaging method could obtain the entirely same form as the primary resonance of the traditional averaging method when researching the first-order approximate solution. And the presented method does not need to introduce the detuning factor as the traditional averaging method. Then the general forms of the approximate solutions of nonlinear system with only polynomial-type displacement nonlinearity are established, which may make the research on this kind of nonlinear system more convenient. At last the validity of the presented method is proved by comparison of the approximate solution and the numerical one of the Duffing oscillator.
2. The revised averaging method
The nonlinear system considered here is:
where is the natural frequency, includes linear damping force, nonlinear damping force and nonlinear restoring force, and is the amplitude and frequency of external excitation respectively.
In traditional averaging method and other perturbation-based methods [14-15], such as multi-scale method, KBM method, it is necessary to consider that whether the excitation frequency is close to the natural frequency, associated with the multiple or fraction of the natural frequency . Hence the solving procedure could be divided into some cases such as the primary resonance, secondary resonance including super-harmonic resonance and sub-harmonic resonance, etc. And some detuning factors should be introduced in the traditional averaging method.
Here we present the revised averaging method, where it is unnecessary to distinguish the above cases and introduce the detuning factor.
Letting the solution of Eq. (1) as:
and
By differentiating Eq. (2a) to , one could obtain:
where . Combined with Eq. (2b), it yields:
By differentiating Eq. (2b) to , one could obtain:
Combined Eq. (5) with Eq. (1), it will yield:
From Eq. (4) and Eq. (6), and by solving the system of equations with and as unknowns, one could get:
and
where .
Applying the averaging procedure to Eq. (7) in a periodic (here ), that means:
Moreover, one could obtain the simpler form as:
3. The traditional averaging method
In traditional averaging method, one must consider the approximation degree of the excitation frequency to the natural frequency , associated with the multiple or the fraction of natural frequency .
3.1. Primary resonance
This case means the excitation frequency is close to the natural frequency . In order to illustrate the approximation degree, one should introduce:
where is a small dimensionless parameter and is the detuning factor. The nonlinear restoring force and the damping force , the amplitude of excitation force should also be re-scaled as:
Then Eq. (1) could be transformed into:
Letting the solution has the form as Eq. (2a) and Eq. (2b), and after the similar deducing procedure, one could obtain:
where .
Averaging the right-hand side of Eq. (13) in a periodic (here ), it would be:
Based on the scale relationship shown in Eq. (11), it could be concluded that Eq. (13) and Eq. (14) are entirely the same as Eq. (7) and Eq. (9). Accordingly, the revised averaging method is totally equal to the primary resonance of the traditional averaging method. Nevertheless, it is unnecessary to introduce the detuning factor in the revised method as the traditional averaging method, which could make the deducing procedure much simpler.
3.2. Super-harmonic resonance
In traditional averaging method, super-harmonic resonance means that the multiple of the excitation frequency is close to the natural frequency, i.e. , where is a natural number unequal to 1. In order to illustrate the approximation degree of to , introducing:
where is a small dimensionless parameter and is the detuning factor. The nonlinear restoring force and the damping force should be rescaled as:
that yields:
The solution should be as:
where:
Based on the standard procedure of averaging method, one can obtain:
where .
Averaging the right-hand side of Eq. (19) in a periodic (here ), it would be:
that could be simplified as:
3.3. Sub-harmonic resonance
In traditional averaging method, sub-harmonic resonance means that the fraction of the excitation frequency is close to the natural frequency, i.e. , where is a natural number unequal to 1. In order to illustrate the approximation degree, introducing:
where is a small dimensionless parameter and is the detuning factor. The nonlinear restoring force and the damping force should be rescaled as:
that yields:
The solution should be as:
where:
Based on the standard procedure of averaging method, one can obtain:
where .
Averaging the right-hand side of Eq. (26) in a periodic (here ), it would be:
that could be simplified as:
4. The general solution of nonlinear system with only polynomial-type displacement nonlinearity
In this section we consider a kind of nonlinear system, where the nonlinear part is only composed of polynomial-type nonlinear restoring force. That means:
4.1. The revised averaging method
From Eq. (29), one could obtain:
In order to obtain the explicit form for Eq. (9), we introduce the expansion forms for the even and odd powers of trigonometric function shown as page 28 in [16] or page 80-82 in [17]:
where is natural number, is the binominal coefficient ().
Based on Eq. (31) and the orthogonality of trigonometric function, the integral in Eq. (9a) is:
The integral in Eq. (9b) is:
when is even, and:
when is odd (supposing ).
Accordingly, when the nonlinear part is only composed of polynomial-type nonlinear restoring force, Eq. (9a) and Eq. (14a) could be as:
and Eq. (9b) and Eq. (14b) could be as:
4.2. The super-harmonic resonance
From Eq. (29), one could obtain:
In order to compute the integral in Eq. (21), the binomial theorem is adopted:
where , is complex number and is the binomial coefficient.
Based on the aforementioned the expansion form for the even and odd powers of trigonometric function and the orthogonality of trigonometric function, the integral in Eq. (21a) is:
The integral in Eq. (21b) is:
when is even, and:
when is odd (supposing ).
Accordingly, Eq. (21) should be as:
4.3. The sub-harmonic resonance
From Eq. (29), one could obtain:
Similarly as the super-harmonic resonance, the integral in Eq. (28a) is:
The integral in Eq. (28b) is:
when is even, and:
when is odd.
Accordingly, Eq. (28) should be as:
when is even, and:
when is odd.
Here only single item of the polynomial-type displacement nonlinearity is considered, but it is still very useful in nonlinear analysis. When several items of polynomial-type displacement nonlinearity exist in the nonlinear system, they could be treated similarly as the above procedure separately.
5. An example – Duffing oscillator
In this section the classical Duffing oscillator is selected as an example to verify the aforementioned results. The Duffing oscillator is as:
where .
5.1. The steady-state solution
Based on Eq. (35), one could obtain the standard equations about the amplitude and phase of the approximate solution as:
Letting and one could obtain the frequency-response equation about the steady-state amplitude as:
It could be found that there maybe exist one or three plus real solution when is changed, that is the reason of jump hysteresis phenomena of the amplitude and had been found in many literatures.
Considering the super-harmonic resonance, then:
and based on Eq. (41), one could obtain the standard equations about the amplitude and phase of free oscillation in the approximate solution as:
Letting and one could obtain the frequency-response equation about the steady-state amplitude and phase for free oscillation for super-harmonic resonance as:
Combining with Eq. (18), one could obtain the super-harmonic response of the Duffing oscillator as:
Considering the sub-harmonic resonance, then:
Based on Eq. (46), one could obtain the standard equations about the amplitude and phase for free oscillation in the approximate solution as:
Letting and one could obtain the frequency-response equation about the non-zero steady-state amplitude and phase of free oscillation for sub-harmonic resonance as:
Combining with Eq. (25), one could obtain the sub-harmonic response of the Duffing oscillator as:
5.2. Numerical simulation
An illustrative example system is studied herein as defined by the basic system parameters , , , , . Fig. 1 illustrates a comparison of the peak values of the approximately analytical solution by the presented method and the numerical solution in the frequency range . The values of the approximately analytical solution are denoted by the solid line, while the values of the numerical results are indicated by the circle. It could be found that the approximately analytical solution agrees very well with the numerical results in the given frequency range except two small regions. The first region is the frequency range for super-harmonic resonance around , where the presented method could not open out the jump and hysteresis phenomenon in this range. But the range is small, and the peak values in this range are not large compared with those of the whole amplitude-frequency curves. The second region is the frequency range for the sub-harmonic resonance larger than , where the presented method could not interpret the multi-value phenomenon of the amplitude, and the amplitude of the sub-harmonic resonance by the numerical integration is large. Nevertheless, the existing range for the sub-harmonic is small, so that one could omit it in many practical engineering.
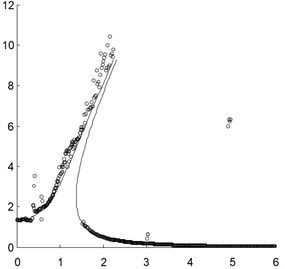
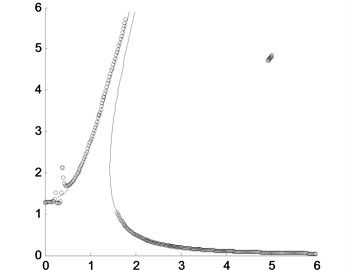
The effects of some important system parameters on the amplitude-frequency are also researched. For example, when the damping coefficient is selected as and , the results are shown in Fig. 2. It could be found that when the damping coefficient is smaller, the difference of the results between the approximately analytical solution and the numerical integration would be larger, and the sub-harmonic resonance would be more distinct. If the damping coefficient is larger, the sub-harmonic resonance would vanish and the two results would agree very well with each other, and the difference of the results between the approximately analytical solution and the numerical integration would be neglectable.
Fig. 1Comparison of the peak values of the approximately analytical solution by the presented method and the direct numerical integration for the basic system parameters: the solid line for the approximately analytical solution and the circles for the direct numerical integration
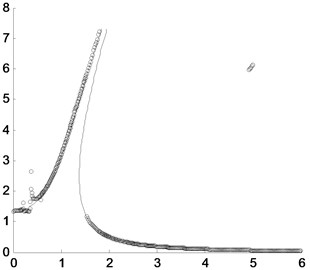
Fig. 2Comparison of the peak values of the approximately analytical solution by the presented method and the direct numerical integration where the solid line is for the approximately analytical solution and the circles are for the direct numerical integration with different damping coefficients: a) c=0.02; b) c=0.6
a)
b)
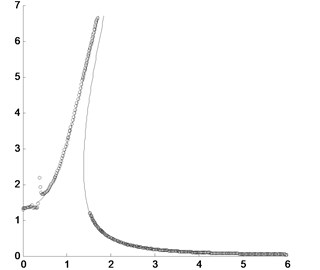
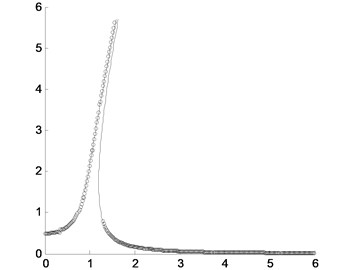
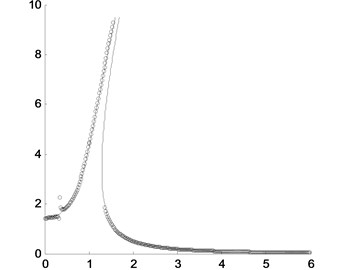
Fig. 3Comparison of the peak values of the approximately analytical solution by the presented method and the direct numerical integration where the solid line is for the approximately analytical solution and the circles are for the direct numerical integration with different amplitudes of excitation force: a) F=0.5; b) F=2.5
a)
b)
When the amplitude of excitation force is changed, for example, and , the amplitude-frequency curves obtained by the presented method and the numerical integration are shown in Fig. 3. It could be found that when the amplitude of excitation force is small enough, the sub-harmonic resonance disappears and the super-harmonic resonance is so small as to be neglectable. If the amplitude of excitation force is large enough, the sub-harmonic and super-harmonic resonance would all be obvious. But the amplitude of super-harmonic resonance and the existing range of sub-harmonic resonance are all small.
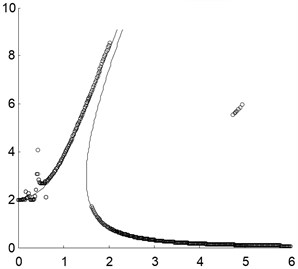
If the nonlinear stiffness coefficient is changed, for example, and , the amplitude-frequency curves obtained by the presented method and the numerical integration are shown in Fig. 4. It could be found that when the nonlinear stiffness coefficient is small, the sub-harmonic resonance would disappear and the super-harmonic resonance is very small. If the nonlinear stiffness coefficient is large enough, the sub-harmonic and super-harmonic resonance would all be clear. But the amplitude of super-harmonic resonance and the existing range of sub-harmonic resonance are still small.
Fig. 4Comparison of the peak values of the approximately analytical solution by the presented method and the direct numerical integration where the solid line is for the approximately analytical solution and the circles are for the direct numerical integration with different nonlinear stiffness coefficients: a) α=0.5; b) α=2.1
a)
b)
Comparatively speaking, the amplitude-frequency curves obtained by the presented method agree well with the numerical integration, which could make us research the nonlinear problems more convenient.
6. Conclusions
In this paper a revised averaging method is presented, which is entirely equal to the results of the primary resonance of the traditional averaging method. It is unnecessary to introduce the small dimensionless parameter and the detuning factor, which makes the solving procedure more convenient. Moreover, the general forms of the approximate solution of nonlinear system with only polynomial-type displacement nonlinearity are obtained. The Duffing oscillator, as an example, is researched and the results show the validity of the presented method.
References
-
Krylov N. N., Bogoliubov N. N. Introduction to Nonlinear Mechanics. Princeton University, Princeton, 1947.
-
Bogoliubov N. N., Mitropolskii Y. A. Asymptotic Methods in the Theory of Nonlinear Oscillations. Gordon and Breach, New York, 1961.
-
Sanders J. A., Verhulst F., Murdock J. Averaging Methods in Nonlinear Dynamical Systems. 2nd ed., Springer Science Business Media, New York, 2007.
-
Burd V. Method of Averaging for Differential Equations on an Infinite Interval: Theory and Applications. Taylor & Francis Group, 2007
-
Wang Z. H., Hu H. Y., Wang H. L. Robust stabilization to non-linear delayed systems via delayed state feedback: the averaging method. Journal of Sound and Vibration, Vol. 279, Issue 3-5, 2005, p. 937-953.
-
Roy R. V. Averaging method for strongly nonlinear oscillators with periodic excitations. International Journal of Non-Linear Mechanics, Vol. 29, Issue 5, 1994, p. 737-753.
-
Chatterjee A. Harmonic balance based averaging: approximate realizations of an asymptotic technique. Nonlinear Dynamics, Vol. 32, Issue 4, 2003, p. 323-343.
-
Kumar D., Datta T. K. Response of nonlinear systems in probability domain using stochastic averaging. Journal of Sound and Vibration, Vol. 302, Issue 1-2, 2007, p. 152-166.
-
Ji J. C., Hansen C. H. Analytical approximation of the primary resonance response of a periodically excited piecewise nonlinear-linear oscillator. Journal of Sound and Vibration, Vol. 278, Issue 1-2, 2004, p. 327-342.
-
Ji J. C., Hansen C. H. On the approximate solution of a piecewise nonlinear oscillator under super-harmonic resonance. Journal of Sound and Vibration, Vol. 283, Issue 1-2, 2005, p. 467-474.
-
Yang X. D., Tang Y. Q., Chen L. Q., Lim C. W. Dynamic stability of axially accelerating Timoshenko beam: averaging method. European Journal of Mechanics A/Solid, Vol. 29, Issue 1, 2010, p. 81-90.
-
Li X. Y., Ji J. C., Hansen C. H. Dynamics of two delay coupled van der Pol oscillators. Mechanics Research Communications, Vol. 33, Issue 5, 2006, p. 614-627.
-
Yang S. P., Chen Y. S. The bifurcations and singularities of the parametrical vibration in a system with Davidenkov's hysteretic nonlinearity. Mechanics Research Communications, Vol. 19, Issue 4, 1992, p. 267-272.
-
Nayfeh A. H., Mook D. T. Nonlinear Oscillations. John Wiley & Sons, INC, 1979
-
Fidlin A. Nonlinear Oscillations in Mechanical Engineering. Springer-Verlag, Berlin, Heidelberg, 2006.
-
Polyanin A. D., Manzhirov A. V. Handbook of Mathematics for Engineers and Scientists. Taylor & Francis Group, LLC, 2007.
-
Bronshtein I. N., Semendyayev K. A., Musiol G., Muehlig H. Handbook of Mathematics. 5th ed., Springer-Verlag, Berlin, Heidelberg, 2007.
About this article
The authors are grateful to the support by National Natural Science Foundation of China (No. 11072158 and 11372198), the Program for New Century Excellent Talents in University (NCET-11-0936), and the Cultivation Plan for Innovation Team and Leading Talent in Colleges and Universities of Hebei Province (LJRC018).
