Abstract
A so-called Spectro-Geometric Method (SGM) is presented for the free transverse vibration analysis of orthotropic thin rectangular plates with arbitrary elastic supports along each of its edges, a class of problems which are rarely attempted in the literature. Regardless of boundary conditions, the displacement function is invariably and simply expressed, in spectral form, as a trigonometric series expansion with an accelerated polynomial rate of convergence as compared with the conventional Fourier series. All the unknown expansion coefficients are treated as the generalized coordinates, and determined using the Rayleigh-Ritz technique. This work allows a capability of modeling a wide spectrum of orthotropic thin rectangular plate under a variety of boundary conditions, and changing the boundary conditions as easily as modifying the material properties or dimensions of the plates. The accuracy and reliability of the SGM prediction are demonstrated though numerical examples. The SGM prediction can be readily and directly extended to other more complicated boundary conditions involving non-uniform restraints, point supports, partial supports and their combinations.
1. Introduction
Orthotropic thin rectangular plates have been widely used in various kinds of engineering such as aeronautic, astronautic and marine structures and so on. This is largely because the orthotropic materials have high strength-to-weight and stiffness-to-weight ratios, which make them ideally suited for use in weight-sensitive structures. The wide use of such structures requires investigating the dynamic characteristics of orthotropic rectangular thin plates in order to develop accurate and reliable design. Therefore, a through understanding of their vibration behavior is essential for engineers and designers.
A well-known monograph about the vibration problems of plates was given by Leissa [1]. Hurlebaus [2] presented an effective and simple solution for obtaining the modal characteristics of orthotropic rectangular plate with completely free boundary conditions. The vibration analysis of orthotropic rectangular plates with various boundary supports were carried out by Ahmadian [3] with superelements technique. Bisnacolini [4] investigated the free vibrations of thin orthotropic rectangular plates with an approximate solution. The vibration characteristics were validated by finite element results. Li [5] investigated the nonlinear vibration characteristics of orthotropic plates based on the higher-order shear deformation theory using differential quadrature method (DQM). Zhu [6] utilized Lagrange equation and modal superposition to study the dynamic behavior of an orthotropic plate under moving loads. Huang [7] developed a discrete method to analyze the free vibration characteristics of orthotropic rectangular plates with variable thickness. Dalaei [8] utilized the extended Kantorovich method to analyze the modal characteristics of clamped rectangular orthotropic plates. Xing [9] studied the free vibration problems of orthotropic rectangular plates using the novel separation of variables. In his work, only the plates with all combinations of simply supported and clamped boundary conditions were investigated. In his following work, he [10] presented the vibration solution for orthotropic rectangular plates with all possible combinations of simply supported, clamped, free and guided conditions. Jafari [11] proposed a simple and efficient mixed Ritz-differential quadrature (DQ) method for free vibration and buckling analysis of orthotropic rectangular plates. The vibration characteristics are obtained and checked against results published in the literature.
From the review of the literature, most of previous studies on orthotropic rectangular plates are confined to the classcical boundary conditions, such as free, simply supported, clamped and their combinations. However, a variety of possible boundary supports encountered in practice engineering applications may not always be classical in nature, and they will always be some elasticity along the supports, and there is a considerable lack of corresponding researches regarding the free transverse vibration of orthotropic rectangular thin plates subjected to arbitrary elastic edge supports.
It is well known that the analytical solutions of vibration characteristics are avaiable for rectangular plates with some particular types of boundary conditions, such as two opposite edges simply supported. A versatile solution to the transverse vibration problem of orthotropic rectangular plates with arbitrary bounday conditions may become possible in light of recent progress in modelling beams [12, 13], plates [14], cylindrical shells [15] and built-up structures [16] with general elastic boundary supports and coupling conditions.
The objective of this investigation is to provide a so-called Spectro-Geometric Method (SGM) for the free transverse vibration analysis of orthotropic thin rectangular plates with arbitrary elastic edge supports. The term “spectro-geometric” has two important implications. Firstly, the geometry of a substructure is accurately described in terms of mathematical or design parameters, rather than a computational grid or mesh. Secondly, an unknown solution variable on each substructure is expressed, in spectral form, as a trigonometric series expansion with an accelerated polynomial rate of convergence. Transverse vibration displacement of the plates, regardless of boundary conditions, is expanded as a standard two-dimensional consine series supplemented with four singe sine functions introduced to eleminate all the relevant discontinuities with the displacement and its derivatives at the edges. In comparison with the Fourier series supplemented by polynomials, this modification is advantageous mathematically because of the “dual-invariance” of trigonometric functions under differential and integral operations. The series expansion coefficients are treated as the generalized coordinates, and determined using Rayleigh-Ritz method. Compared with most of the existing techniques, the current approach can be applicable to arbitrary boundary supports without any modifying any special procedures schemes. Several numerical examples are presented to verify the reliability and accuracy of the SGM predition and to demonstrate the flexibility in dealing with different boundary conditions.
2. Theoretical formulation
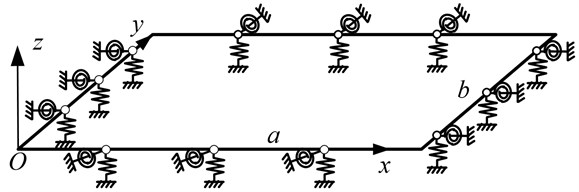
As shown in Fig. 1, an orthotropic thin rectangular plate with arbitrary elastic edge supports is depicted in a Cartesian coordinate system (, , , ). The plate has the constant thickness . and are the length and width of the thin rectangular plate, respectively. The transverse vibration displacement on the middle surface of the plate is denoted by . The arbitrary elastic edge supports are imposed by setting two types of uniformly distributed restraining springs (linear and rotational springs) with independent stiffness values along each edge. The stiffness distribution function for each type of elastic restraint can be specified independently and vary continuously or discontinuously along an edge. In this way, the elastic restraints not only themselves represent a class of boundary conditions of practical interest, but also can be used to unite all the classical homogeneous boundary conditions by accordingly setting the stiffness constants equal to either zero or infinity. For example, a clamped edge (C) refers to a special case of the elastic supports when the stiffnesses for both of the (linear and rotational) restraining springs become infinity (represented by 1013 in the numerical calculations). The free edge (F) can be readily achieved by setting the stiffness values to zero for the two sets of springs. The simply supported case (S) for the transverse vibration motion can be created by specifying the infinite stiffness for the linear springs, and zero stiffness for the rotational springs. Thus, the boundary conditions for a plate are fully specified by using four letters with the first one indicating the boundary support along the first edge, 0. The remaining (the second to the fourth) edges are ordered in the counterclockwise direction.
Fig. 1An orthotropic thin rectangular plate with elastically restrained edge
The governing differential equation for the transverse vibration of an orthotropic thin rectangular plate can be expressed as [17]:
where are the standard bending rigidities in the classical lamination theory, is the mass density of the plate, is the frequency of the harmonic motion.
For an orthotropic plate, the stiffness constants can be expressed with the lamina engineering constants and plate thickness in the form of:
An orthotropic material is characterized by the fact that the mechanical elastic properties have two perpendicular planes of symmetry. Due to this only four elastic constants , , and are independent, the coefficient can be determined according to the following relation:
In terms of the transverse vibration displacement , the boundary conditions for a generally supported orthotropic thin rectangular plate can be expressed as:
where and ( and ) are the linear spring constants, and and ( and ) are the rotational spring constants at 0 and (0 and ), respectively.
In order to model the transverse vibration problem of orthotropic thin rectangular plate with arbitrary elastic edge supports, the transverse vibration displacement is universally sought in spectral form as an accelerated trigonometric series expansion as:
where denotes the unknown series expansion coefficient to be determined:
In the SGM model, the geometries for the plate can be fully and conveniently defined by the coordinates of several key points or other relevant parameters, rather than being approximated by a mesh consisting of a number of nodes and elements as typically associated with the existing methods. More importantly, the parametric description of the plate will allow an automatic change or update of the model without the need of “re-meshing”. This has profound implications to sensitivity studies, optimization, uncertainty analysis, and statistical or stochastic predictions. From a practical point of view, this automated analysis capability can lead to a substantial reduction of the time spent on creating computational models, the major cost concern with CAE analyses nowadays.
The four sine terms in both - and -directions are introduced to eliminate the potential discontinuities (or jumps), along the edges of the plate, of the displacement functions when it is periodically extended and expressed as a trigonometric series expansion. As a result, the Gibbs effect can be eliminated and the convergence rate of the series expansion can be adequately improved. Mathematically, it can be proven that the series expansion given in Eq. (8) converges uniformly and polynomially over the rectangular solution domain. As a matter of fact, Eq. (8) is able to expand and uniformly converge to any function for . Also, any secondary variables of interest can be readily obtained from appropriate mathematical operations.
In practice, the solution in the form of Eq. (8) can be obtained in both strong and weak forms. In seeking a strong form of solution, the series will have to satisfy both governing differential equations and boundary conditions exactly on a point-wise basis. This solution process has been used to determine the in-plane [18] and out-of-plane [19] vibrations of rectangular plates although different forms of series expressions were used there. From the standpoint of numerical implementations, it is often much easier to find a weak form of solution based on a variational or energy principle. In such a case, all the series expansion coefficients will be treated as the generalized coordinates which are independent from each other. The final system of equations can be readily derived from, for example, the Rayleigh-Ritz technique. When the solution is constructed sufficiently smooth, the weak solution is mathematically equivalent to the strong form. The weak form of solution will be sought here since it will be more attractive in modeling complex structures.
The Lagrangian function of the orthotropic thin rectangular plate can be eventually written as:
where and denote the total potential energy and the total kinetic energy, respectively. For the plate model shown in Fig. 1, the total potential energy, including the transverse vibration strain energy and the potential energy stored in the boundary springs, can be written as:
By neglecting rotary inertia, the kinetic energy of the plate is expressed as:
Substituting the displacement expression, Eq. (8), into the Lagrangian, Eq. (11) and minimizing it against all the unknown series expansion coefficients, one can obtain a system of linear algebraic equations as:
where:
denotes the vector that contains all the unknown series expansion coefficients; and are the stiffness and mass matrices, respectively.
The natural frequencies and eigenvectors now can be easily determined from solving a standard matrix eigenvalue problem, Eq. (14). Each of the eigenvectors actually contains the series expansion coefficients for the corresponding mode. The physical mode shapes can be simply obtained by using Eq. (8). Although this investigation is focused on the free vibration of orthotropic thin rectangular plates, the dynamic responses to an applied load can be easily determined by including its work in the Lagrangian, eventually resulting in a force term on the right side of Eq. (14).
It should also be noted that the current method is particularly advantageous in obtaining other variables of interest such as power flows through appropriate mathematical operations in an analytical manner. Since the displacement is constructed to be sufficiently smooth, the mathematical operations can be directly applied to the displacement expansions term-by-term as warranted by the property of absolute and uniform convergence. For example, the vibration velocity can be easily written as the product of displacement and factor of for the case of harmonic motion with time factor of , and also give the structural mobility which is defined as the ratio of vibration velocity to external force.
3. Results and discussions
In this section, several numerical examples will be carried out to demonstrate the correctness of the current method for the free transverse vibration analysis of orthotropic thin rectangular plates as well as the code written. Numerical analyses are subsequently performed to obtain the transverse vibration characteristics of orthotropic thin rectangular plates subject to various boundary conditions. For orthotropic thin rectangular plates, the material properties need to be specified include 208 GPa, 18.9 GPa, 5.7 GPa, 2000 kg/m3, and 0.23. The thickness 0.02 m is used in the following numerical calculations.
First, consider an orthotropic rectangular thin plate which is fully clamped along each edge (C-C-C-C). The plate has an aspect ratio 1. The first ten dimensionless frequency parameters, , are listed in Table 1 for different series truncation numbers: 4, 5, …, 12. Two sets of reference results taken from [9] and obtained using an FEM (ABAQUS) model are also given there. A good convergence behavior is observed. Of equal importance, the solution also shows an excellent numerical stability, meaning that the values essentially remain the same as the truncation numbers become increasingly large. Once the convergence behavior is understood, the series will be consistently truncated to 10 in all the subsequent calculation.
Table 1Frequency parameters Ω=aω2ρh/D14 for a C-C-C-C plate (b/a= 1)
Mode sequence | ||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
4 | 4.88 | 5.53 | 6.70 | 7.93 | 8.17 | 8.18 | 8.74 | 9.64 | 9.90 | 10.92 |
5 | 4.88 | 5.52 | 6.70 | 7.92 | 8.17 | 8.17 | 8.73 | 9.64 | 9.90 | 10.92 |
6 | 4.88 | 5.52 | 6.70 | 7.92 | 8.17 | 8.17 | 8.73 | 9.64 | 9.76 | 10.82 |
7 | 4.88 | 5.52 | 6.70 | 7.92 | 8.16 | 8.17 | 8.73 | 9.64 | 9.76 | 10.82 |
8 | 4.88 | 5.52 | 6.70 | 7.92 | 8.16 | 8.17 | 8.73 | 9.63 | 9.76 | 10.82 |
9 | 4.88 | 5.52 | 6.70 | 7.92 | 8.16 | 8.17 | 8.73 | 9.63 | 9.76 | 10.82 |
10 | 4.88 | 5.52 | 6.70 | 7.92 | 8.16 | 8.17 | 8.73 | 9.63 | 9.76 | 10.82 |
11 | 4.88 | 5.52 | 6.70 | 7.92 | 8.16 | 8.17 | 8.73 | 9.63 | 9.76 | 10.82 |
12 | 4.88 | 5.52 | 6.70 | 7.92 | 8.16 | 8.17 | 8.73 | 9.63 | 9.76 | 10.82 |
Ref. [9] | 4.87 | 5.50 | 6.68 | 7.91 | 8.15 | 8.16 | 8.72 | 9.62 | 9.75 | 10.81 |
FEM | 4.88 | 5.52 | 6.69 | 7.91 | 8.16 | 8.17 | 8.72 | 9.62 | 9.75 | 10.81 |
Next, consider a completely free orthotropic rectangular (F-F-F-F). The completely free boundary condition represents a classical, but quite challenging, case for testing a plate solution. The first ten frequency parameters, , are listed in Table 2 for orthotropic thin rectangular plates with different aspect ratios. The numerical results calculated using an FEM (ABAQUS) model are also given there for comparison. These two sets of solutions agree well with each other.
Table 2Frequency parameters Ω=aω2ρh/D14 for an F-F-F-F plate
Method | Mode sequence | ||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
1.0 | Present | 1.96 | 2.59 | 3.22 | 4.31 | 4.68 | 4.73 | 4.87 | 5.31 | 6.04 | 6.14 |
FEM | 1.96 | 2.59 | 3.21 | 4.30 | 4.68 | 4.73 | 4.86 | 5.31 | 6.03 | 6.13 | |
2.0 | Present | 1.30 | 1.37 | 2.05 | 2.15 | 2.73 | 3.02 | 3.45 | 3.88 | 4.22 | 4.72 |
FEM | 1.30 | 1.37 | 2.05 | 2.15 | 2.73 | 3.01 | 3.45 | 3.88 | 4.22 | 4.71 | |
3.0 | Present | 0.86 | 1.11 | 1.44 | 1.62 | 2.01 | 2.08 | 2.55 | 2.58 | 3.04 | 3.16 |
FEM | 0.86 | 1.11 | 1.44 | 1.62 | 2.01 | 2.08 | 2.55 | 2.58 | 3.03 | 3.16 | |
To further validate the accuracy and reliability of the SGM, the orthotropic thin rectangular plates with different aspect ratios are studied under various restraining conditions. Presented in Table 3 are the first ten frequency parameters, , for plates which is simply supported along all of its edges. Due to a lack of analytical solutions, the numerical results calculated using an FEM (ABAQUS) model are given there for comparisons. Since the reference solutions for orthotropic rectangular plates are scarce, the plates with other classical boundary conditions are also studied systematically and the corresponding results are listed in Tables 4-5. Such results can be particularly useful in benchmarking other solution methods. Traditionally, the displacement expressions and the subsequent solution algorithms and implementations are dictated by the intended boundary condition. Consequently, most studies are specifically related to a particular type of boundary conditions. In the above examples, it has been demonstrated that the proposed SGM prediction model can be lightly applied to arbitrary elastic edge supports with no need of making any algorithm or procedural modifications; the modifying boundary conditions is as simple as changing plate parameters such as geometrical and material properties.
Table 3Frequency parameters Ω=aω2ρh/D14 for an S-S-S-S plate
Method | Mode sequence | ||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
1.0 | Present | 3.32 | 4.15 | 5.55 | 6.35 | 6.63 | 7.14 | 7.28 | 8.31 | 8.80 | 9.47 |
FEM | 3.32 | 4.15 | 5.54 | 6.35 | 6.63 | 7.14 | 7.27 | 8.30 | 8.79 | 9.46 | |
2.0 | Present | 3.18 | 3.32 | 3.64 | 4.15 | 4.81 | 5.55 | 6.30 | 6.33 | 6.35 | 6.45 |
FEM | 3.18 | 3.32 | 3.64 | 4.15 | 4.81 | 5.54 | 6.30 | 6.33 | 6.35 | 6.45 | |
3.0 | Present | 3.16 | 3.21 | 3.32 | 3.51 | 3.79 | 4.15 | 4.58 | 5.05 | 5.55 | 6.07 |
FEM | 3.16 | 3.21 | 3.32 | 3.51 | 3.79 | 4.15 | 4.58 | 5.05 | 5.54 | 6.06 | |
Table 4Frequency parameters Ω=aω2ρh/D14 for a C-S-C-F plate
Method | Mode sequence | ||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
1.0 | Present | 4.74 | 4.87 | 5.39 | 6.43 | 7.83 | 7.86 | 7.94 | 8.17 | 8.67 | 9.39 |
FEM | 4.74 | 4.87 | 5.39 | 6.43 | 7.82 | 7.86 | 7.94 | 8.17 | 8.66 | 9.38 | |
2.0 | Present | 4.73 | 4.76 | 4.83 | 4.99 | 5.28 | 5.71 | 6.26 | 6.92 | 7.63 | 7.85 |
FEM | 4.73 | 4.76 | 4.83 | 4.99 | 5.27 | 5.70 | 6.26 | 6.91 | 7.62 | 7.85 | |
3.0 | Present | 4.73 | 4.74 | 4.77 | 4.82 | 4.90 | 5.04 | 5.24 | 5.50 | 5.83 | 6.21 |
FEM | 4.73 | 4.74 | 4.77 | 4.82 | 4.90 | 5.04 | 5.24 | 5.50 | 5.83 | 6.20 | |
Table 5Frequency parameters Ω=aω2ρh/D14 for a C-F-F-F plate
Method | Mode sequence | ||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
1.0 | Present | 1.87 | 2.06 | 2.99 | 4.47 | 4.69 | 4.79 | 5.14 | 5.91 | 6.13 | 7.06 |
FEM | 1.87 | 2.06 | 2.99 | 4.47 | 4.69 | 4.79 | 5.14 | 5.90 | 6.13 | 7.05 | |
2.0 | Present | 1.87 | 1.93 | 2.14 | 2.61 | 3.28 | 4.05 | 4.69 | 4.72 | 4.79 | 4.87 |
FEM | 1.87 | 1.93 | 2.14 | 2.61 | 3.28 | 4.05 | 4.69 | 4.72 | 4.78 | 4.86 | |
3.0 | Present | 1.87 | 1.90 | 1.98 | 2.17 | 2.49 | 2.91 | 3.39 | 3.91 | 4.45 | 4.69 |
FEM | 1.87 | 1.90 | 1.98 | 2.17 | 2.49 | 2.91 | 3.39 | 3.91 | 4.44 | 4.69 | |
All the examples considered thus far have been limited to the classical edge supports which are viewed as the special cases of elastically restrained edges. We now turn to orthotropic thin rectangular plates with arbitrary elastic edge supports. First consider a simply supported orthotropic thin rectangular plate, but with uniform rotational restraint (stiffness constants for rotational springs represent by ), along each edge. The calculated frequency parameters are given in Table 6 together with the FEM results. The second example deals with a cantilever plate (clamped at 0) with identical elastic restraints at other edges. While the linear stiffness of the linear springs is fixed to 106 N/m, the rotational springs will be specified to take various stiffness values: 100, 104, 108 and 1012 Nm/rad. The corresponding frequency parameters are shown in Table 7. In all the cases, a good agreement is observed between the current solution and the FEM results. The third example considers an orthotropic thin rectangular plate elastically restrained along all the edges. The stiffnesses for the linear and rotational restraining springs are set equal to 106 N/m and 107 Nm/rad, respectively. The first ten frequency parameters are shown in Table 8. For any given modal frequency, the corresponding physical mode shape can be lightly determined from Eq. (8). As an example, the mode shapes for the plate with 1 are plotted in Fig. 2.
Table 6Frequency parameters Ω=aω2ρh/D14 for simply supported plates with uniform rotational restraint along all the edges (b/a= 2)
Method | Mode sequence | ||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
100 | Present | 3.18 | 3.32 | 3.64 | 4.15 | 4.81 | 5.55 | 6.30 | 6.33 | 6.35 | 6.45 |
FEM | 3.18 | 3.32 | 3.64 | 4.15 | 4.81 | 5.54 | 6.30 | 6.33 | 6.35 | 6.45 | |
104 | Present | 3.20 | 3.34 | 3.67 | 4.18 | 4.83 | 5.57 | 6.31 | 6.35 | 6.36 | 6.47 |
FEM | 3.20 | 3.34 | 3.67 | 4.18 | 4.83 | 5.57 | 6.31 | 6.35 | 6.36 | 6.47 | |
108 | Present | 4.74 | 4.82 | 4.99 | 5.32 | 5.79 | 6.38 | 7.05 | 7.79 | 7.84 | 7.88 |
FEM | 4.74 | 4.81 | 4.99 | 5.32 | 5.79 | 6.37 | 7.05 | 7.78 | 7.84 | 7.88 | |
1012 | Present | 4.75 | 4.83 | 5.01 | 5.33 | 5.80 | 6.38 | 7.06 | 7.80 | 7.86 | 7.90 |
FEM | 4.75 | 4.83 | 5.01 | 5.33 | 5.79 | 6.38 | 7.06 | 7.79 | 7.86 | 7.90 | |
Table 7Frequency parameters Ω=aω2ρh/D14 for C-F-F-F plates with identical elastic restraint at “free” edges (b/a= 1)
Method | Mode sequence | ||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
100 | Present | 2.61 | 2.98 | 3.57 | 4.70 | 4.79 | 4.93 | 5.29 | 6.01 | 6.22 | 7.12 |
FEM | 2.60 | 2.98 | 3.58 | 4.69 | 4.79 | 4.93 | 5.28 | 6.00 | 6.21 | 7.11 | |
104 | Present | 2.62 | 2.98 | 3.61 | 4.77 | 4.81 | 4.94 | 5.31 | 6.04 | 6.28 | 7.16 |
FEM | 2.62 | 2.99 | 3.62 | 4.76 | 4.81 | 4.94 | 5.30 | 6.04 | 6.28 | 7.15 | |
108 | Present | 2.79 | 3.08 | 3.93 | 5.37 | 5.53 | 5.62 | 5.94 | 6.69 | 7.01 | 7.85 |
1012 | Present | 2.79 | 3.08 | 3.93 | 5.38 | 5.54 | 5.63 | 5.94 | 6.69 | 7.01 | 7.86 |
Table 8Frequency parameters Ω=aω2ρh/D14 for orthotropic thin rectangular plates with elastic restraints at all four edges: k= 106 N/m and K= 107 Nm/rad
Method | Mode sequence | ||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
1.0 | Present | 2.25 | 2.66 | 3.40 | 3.62 | 3.69 | 4.33 | 5.25 | 5.62 | 6.25 | 6.33 |
FEM | 2.25 | 2.66 | 3.40 | 3.63 | 3.69 | 4.33 | 5.25 | 5.61 | 6.25 | 6.33 | |
2.0 | Present | 2.01 | 2.22 | 2.50 | 2.95 | 3.35 | 3.42 | 3.56 | 3.62 | 3.83 | 4.28 |
3.0 | Present | 1.95 | 2.04 | 2.21 | 2.43 | 2.72 | 3.11 | 3.33 | 3.37 | 3.43 | 3.53 |
Fig. 2The mode shapes for an orthotropic rectangular plate (b/a= 1) with elastic restraints, k= 106 N/m and K= 107 Nm/rad, along each edge: the a) first, b) second, c) third mode
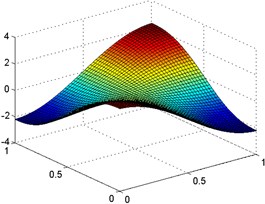
a)
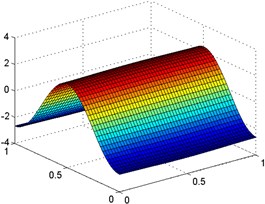
b)
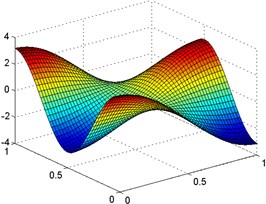
c)
Finally, the vibration behavior of orthotropic rectangular plate under the combinations of point supported and partially supported boundary conditions is investigated. The first ten frequency parameters for the point supported and partially supported orthotropic rectangular plates are listed in Table 9. The boundary support arrangements along each edge are illustrated in Fig. 3. In this support arrangement, the plate is point supported at the center of edges (0 and ), and partially supported with the edge (0, /4) and (3/4, ) of the edges (0 and ). Some selected mode shapes are plotted in Fig. 4. It can be seen that the current solutions agree well with the FEM results.
Table 9Frequency parameters Ω=aω2ρh/D14 for plate with point and partially supported boundary conditions
Method | Mode sequence | ||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
1.0 | Present | 3.67 | 4.16 | 4.74 | 5.07 | 5.69 | 5.84 | 6.10 | 7.17 | 7.23 | 7.98 |
FEM | 3.66 | 4.16 | 4.73 | 5.05 | 5.68 | 5.83 | 6.09 | 7.17 | 7.23 | 7.97 | |
2.0 | Present | 2.18 | 2.40 | 2.61 | 2.78 | 3.60 | 3.74 | 4.23 | 4.42 | 4.69 | 4.93 |
3.0 | Present | 1.48 | 1.66 | 1.91 | 2.00 | 2.58 | 2.69 | 2.99 | 3.11 | 3.57 | 3.70 |
Fig. 3Point and partially supported boundary conditions for plates
Fig. 4Mode shapes for an orthotropic rectangular plate (b/a= 1) with point supported and partially supported boundary conditions: the a) fifth, b) eighth, c) ninth mode
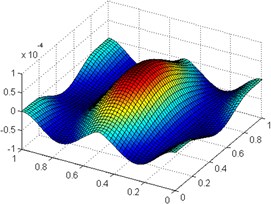
a)
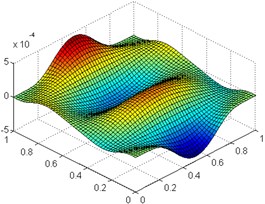
b)
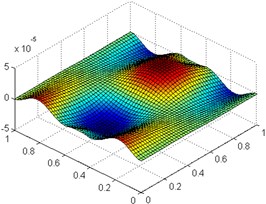
c)
4. Conclusions
A meshless and parametric modeling method, the so-called Spectro-Geometric Method (SGM), is presented for the free transverse vibration analysis of orthotropic thin rectangular plates with arbitrary elastic restraints along each edge, which allows treating the classical homogenous boundary conditions as the special cases when the stiffness for each of the restraining spring is equal to zero or infinity. The term “spectro-geometric” implies: 1) the geometry of a structural component is accurately described in terms of mathematical or design parameters, and 2) the primary variables are sought, in spectral form, as a trigonometric series expansion with an accelerated rate of convergence. Unlike in most existing studies where solutions are often developed for a specified type of boundary conditions, the SGM prediction can generally applied to a wide spectrum of boundary conditions with no need of modifying solution algorithms and procedures. The prominent convergence and accuracy of the SGM have been proved through a number of numerical examples on free vibrations of orthotropic thin rectangular plates. Although the stiffness for each restraining springs is here assumed to be uniform, any non-uniform, discrete, or partial stiffness distribution can be readily considered by accordingly modifying potential energies given in Eq. (12).
References
-
Leissa A. W. Vibration of Plates. U. S. Government Printing Office, Washington DC, 1969.
-
Hurlebaus S., Gaul L., Wang J. T. S. An exact series solution for calculating the eigenfrequencies of orthotropic plates with completely free boundary. Journal of Sound and Vibration, Vol. 244, Issue 5, 2001, p. 747-759.
-
Ahmadian M. T., Sherafati Zangeneh M. Vibration analysis of orthotropic rectangular plates using superelements. Computer Methods in Applied Mechanics and Engineering, Vol. 191, Issue 19-20, 2002, p. 2097-2103.
-
Biancolini M. E., Brutti C., Reccia L. Approximate solution for free vibrations of thin orthotropic rectangular plates. Journal of Sound and Vibration, Vol. 288, Issue 1-2, 2005, p. 321-344.
-
Li J. J., Cheng C. J. Differential quadrature method for nonlinear vibration of orthotropic plates with finite deformation and transverse shear effect. Journal of Sound and Vibration, Vol. 281, Issue 1-2, 2005, p. 295-309.
-
Zhu X. Q., Law S. S. Dynamic behavior of orthotropic rectangular plates under moving loads. Journal of Engineering Mechanics, 2003, Vol. 129, Issue 1, p. 79-87.
-
Huang M., Ma X. Q., Sakiyama T., Matuda H., Morita C. Free vibration analysis of orthotropic rectangular plates with variable thickness and general boundary conditions. Journal of Sound and Vibration, Vol. 288, Issue 4-5, 2005, p. 931-955.
-
Dalaei M., Kerr A. D. Natural vibration analysis of clamped rectangular orthotropic plates. Journal of Sound and Vibration, Vol. 189, Issue 3, 1996, p. 399-406.
-
Xing Y. F. Liu B. New exact solutions for free vibrations of thin orthotropic rectangular plates. Composite Structures, Vol. 89, Issue 4, 2009, p. 567-574.
-
Xing Y. F., Xu T. F. Solution methods of exact solutions for free vibration of rectangular orthotropic thin plates with classical boundary conditions. Composite Structures, Vol. 104, 2013, p. 187-195.
-
Jafari A. A., Eftekhari S. A. An efficient mixed methodology for free vibration and buckling analysis of orthotropic rectangular plates. Applied Mathematics and Computation, Vol. 218, Issue 6, 2011, p. 2670-2692.
-
Li W. L. Free vibrations of beams with general boundary conditions. Journal of Sound and Vibration, Vol. 237, Issue 4, 2000, p. 709-725.
-
Li W. L., Bonilha M. W., Xiao J. Vibrations of two beams elastically coupled together at an arbitrary angle. Acta Mechanica Solida Sinica, Vol. 25, Issue 1, 2012, p. 61-72.
-
Li W. L. Vibration analysis of rectangular plates with general elastic boundary supports. Journal of Sound and Vibration, Vol. 273, Issue 3, 2004, p. 619-635.
-
Li W. L. Vibrations of circular cylindrical shells with general elastic boundary restraints. Journal of Vibration and Acoustics, Vol. 135, Issue 2, 2013, p. 024501.
-
Jiang S. L., Li W. L., Yang T. J. A spectro-geometric method for the vibration analysis of built-up structures. Noise Conference Proceedings, 2013, p. 1-6.
-
Khov H., Li W. L., Gibson R. F. An accurate solution method for the static and dynamic deflections of orthotropic plates with general boundary conditions. Composite Structures, Vol. 90, Issue 4, 2009, p. 474-481.
-
Du J. T., Li W. L., Jin G. Y., Yang T. J., Liu Z. G. An analytical method for the in-plane vibration analysis of rectangular plates with elastically restrained edges. Journal of Sound and Vibration, Vol. 306, Issue 3-5, 2007, p. 908-927.
-
Li W. L., Zhang X. F., Du J. T., Liu Z. G. An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports. Journal of Sound and Vibration, Vol. 321, Issue 1-2, 2009, p. 254-269.
About this article
The authors would like to thank anonymous reviewers for their constructive comments. The work was supported by the International S&T Cooperation Program of China (ISTCP, Grant No. 2011DFR90440), the key project of the National Natural Science of Foundation of China (Grant No. 50939002) and China Scholarship Council (Grant No. 2011668004).
