Abstract
The mathematical model of MR fluid flow in an annular channel of the MR shock-absorber taking into account forces of dry friction and gas friction in a pneumatic camera, dependence rheological properties of the MR fluid on shear rate, temperature and magnetic flux density is developed. Performance characteristics of the MR shock-absorber (dependences of force on value of control electric signal taking into account of shock-absorber geometry, rod displacement, rheological properties of MR fluid, temperature) are calculated. The analysis of influence of the magnetic field and temperature values on the MR shock-absorber performance characteristics depending on amplitudes and frequencies of piston movement is carried out. The resistance force with growth of magnetic flux density increases 40 times. But the resistance force with growth of temperature from 20°C to 80°C decreases 7 times, in an magnetic field ( 500 mT), and 2 times, without a field ( 0 mT).
1. Introduction
Now active development of new compositions of magnetorheological (MR) fluids, theoretical and experimental research of their rheological properties and search of their practical application in the technician are conducted [1-3].
The most demanded application area of MR fluids is the machinery construction [3, 4]. In the scientific and technical literature various variants of active and semi-active cushion systems are considered [1, 3, 4]. In such systems one of the main elements is the controlled shock-absorber with MR fluid, named MR shock-absorber. Last years necessity of development of MR shock-absorber mathematical models and numerical estimation of its performance characteristics increases by reason of occurrence of large quantity of MR fluid compositions with various rheological properties [1, 2, 4].
Temperature factor has significant influence on rheological properties of a MR fluid, but we were not found sufficient information to describe performances characteristics of controllable shock-absorbers and any control algorithm for electronic control units taking into account of temperature. The designing of new geometry of MR shock-absorber and its elements by development of controlled cushion systems of the concrete vehicle is usually required [4, 5].
The aim of this work is simulation and analysis of performance characteristics of the designed MR shock-absorber taking into account rheological properties of MR fluid, influence of the magnetic field, temperature and such as modes of dynamic rod load under the harmonic law.
2. Problem statement
Fig. 1 shows the scheme of the magnetorheological shock-absorber and its basic elements. Hydraulic resistance is created in the annular channels 5 (Fig. 1), thus the area 3 of the channels 5 defines a regulation zone of MR fluid viscosity at influence by the magnetic field.
Fig. 1The scheme of the MR shock-absorber: 1 – the cylinder; 2 – a MR fluid without a magnetic field; 3 – a MR fluid in the magnetic field; 4 – the piston; 5 – the annular channel; 6 – the solenoid; 7 – magnetic field lines; 8 – the rod; 9 – the pneumatic camera with a gas
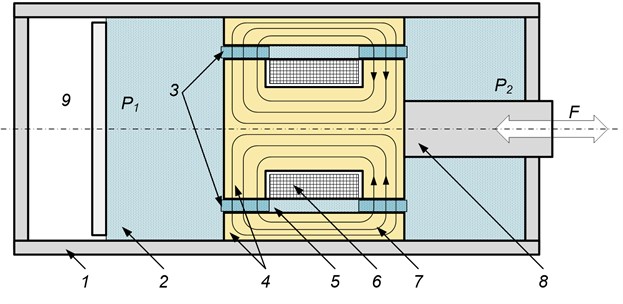
At electric current, giving on the solenoid 6 (Fig. 1), creates the magnetic field with the flux 7 passing through the core which represents the piston 4 rigidly connected with the rod 8 and located in the shock-absorber cylinder 1.
Resistance force of a telescopic MR shock-absorber, depending on time , is defined from the equation system [5]:
where:
where , , is forces of dry friction, gas friction in a pneumatic camera and hydraulic resistance of MR fluid in an annular channel. The inertia force of a MR shock-absorber piston is neglected [4, 5]; and is the area of cross-section section of a piston and a rod accordingly; and is the parameters, which define dry force from an experiment; is the index of power; is the time; is the pressure drop; is the piston velocity; , is the coordinates; , is the piston and rod radii; , is the internal and external radii of a channel; is the initial piston position; is the magnetic flux density; is the temperature.
Let’s define the pressure drop in an orifice channel of the piston. A flow of an incompressible viscoplastic MR fluid in the annular channel at the cylindrical coordinate system is described by the equation system, which contains movement equation, rheological equation and continuity equation:
where is the apparent viscosity; is the velocity; is the pressure; is the density of MR fluid; is the volume flow. Volume flow of MR fluid in the channel is defined [4] from the sinusoidal law of piston displacement with defined values of frequency and amplitude :
We use net method [6] for calculation of Eq. (5)–(7).
MR fluid is considered motionless, and the no-slip conditions are set on walls of an annular channel:
The MR fluid has been developed in A.V. Luikov Heat and Mass Transfer Institute of the National Academy of Sciences of Belarus [2].
Measurements of rheological properties of the MR fluid have been executed in a range of shear rates 0.01-1000 s-1 on Rheometer “Physica MCR 301” of manufacturer “Anton Paar” with a measuring cell “MRD70”.
3. Results and discussion
In this work, performance characteristics of the magnetorheological shock-absorber, which is used for a controlled vibroprotective system, are modelled and numerically evaluated.
Rheological curves are constructed for the experiments at various values of magnetic flux density [2]. All of them can be described by viscoplastic model Herschel-Bulkley:
where parameters of dynamic yield stress , plastic viscosity and index of power depend on magnetic flux density [in scale of mT] and temperature accordingly:
Overall relative variation coefficient of Herschel-Bulkley model is equal 9.8 %, that precisely enough describes viscoplastic behaviour of the MR fluid at different magnetic flux density in the range 0-500 mT and temperature 20°C [7]. The temperature dependence of yield stress and plastic viscosity was defined as an approximation of rheological curves of dispersion media of MR fluid from temperature. As a result, this rheological model (see Eqs. (11–14)) allows to define the general calculated dependence of shear stress on shear rate, temperature and magnetic flux density (Fig. 2).
Having defined rheological state equation in a form of Herschel-Bulkley model and dependences its parameters (yield stress, plastic viscosity, index of power) on magnetic flux density, the problem of MR fluid flow in an annular channel of a controlled shock-absorber taking into account construction geometry, external influence of the magnetic field and conditions of dynamic rod loading can be solved.
Fig. 2The dependence of shear stress τ of the MR fluid on shear rate and different values of magnetic flux density: 1 – T= 20°C; 2 – T= 40°C; 2 – T= 80°C
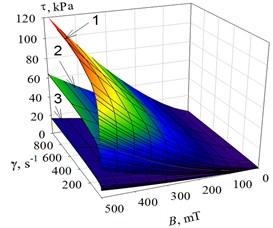
Fig. 3The dependence of MR shock-absorber force from rod displacement z at different values of magnetic flux density B and temperature T: 1 – B= 0 mT; 2 – 200; 3 – 500
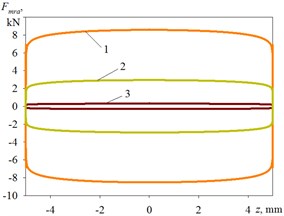
a)5 mm, 1 Hz, 20°C
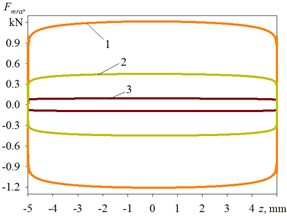
b)5 mm, 1 Hz, 80°C
For calculation of performance characteristics of the MR shock-absorber we use following data: 0,008 m; 0,02 m; 0,016 m; 0,017 m; 0,03 m; 0,01 m; 10 MPa; 0,00009 m3; 2600 kg/m3; 60 Н; 3·10-6 N/Pa; 0,08 m.
Results of numerical modelling of MR shock-absorber force are resulted in Fig. 3 at rod motion under the harmonic law with amplitude of 1, 5 and 40 mm, frequency of 0.5, 1 and 3 Hz, temperature of 20 and 80°C, magnetic flux density of 0, 200 and 500 mT. For the purpose of simplification it is admissible that the force component is equal to zero.
Estimation of the maximum resistance force on the rod was realized in the rebound stroke of the MR shock-absorber due to the fact that the resistance force acting on the rod in the compression stroke for this shock-absorber design is equal the resistance force acting on the rod in the rebound stroke. The result of experimental data processing is shown in Fig. 4 as the dependences of the maximum resistance force of the MR shock-absorber (at rebound stroke) on the magnetic flux density and temperature by the harmonical law , where is the amplitude of displacement, is the frequency, and is the time. Fig. 4 shows, that that resistance force grows with the magnetic flux density at different piston velocities . So, the force at the velocity 0.0314 m/s in an magnetic field (500 mT) and without a field (0 mT) increases 32 times, when 20°C, and at 80°C, 13 times.
The force increases with growth of magnetic flux density (see Table 1), for example: 196 N (at 0.5 Hz) and 302 N (at 3 Hz) at the absence of a magnetic field, 6846 N (at 0.5 Hz) and 8577 N (at 3 Hz) at magnetic flux density 500 mT and amplitude 5 mm. The force decreases with growth of temperature (see Table 2), for example: 263 N and 395 N at the absence of a magnetic field, 8781 N and 10198 N at magnetic flux density 500 mT and amplitude 20 mm. Similar result was obtained for the case, when is equal 1, 5, 40 mm.
Fig. 4The dependence of the MR shock-absorber force on magnetic flux density B and temperature T at different values of piston velocity vp: 1 – vp= 0.0031 m/s; 2 – 0.0314; 3 – 0.6283
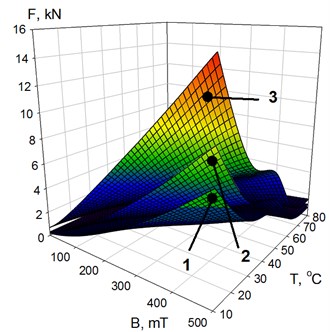
Table 1Estimation of the performance characteristics of the controlled MR shock-absorber at magnetic flux density B= 0 and 500 mT (temperature T= 20°C)
, mm | , Hz | , N | ||
at 0 mT | at 500 mT | |||
1 | 0.5 | 141 | 5669 | 40.1 |
3 | 204 | 6999 | 34.2 | |
5 | 0.5 | 196 | 6846 | 34.9 |
3 | 302 | 8577 | 28.4 | |
40 | 0.5 | 325 | 8907 | 27.4 |
3 | 531 | 11346 | 21.3 | |
Thus, the coefficient of relative increase of force (500 mT)(500 mT) is equal 40.1 and 21,3 times for different loading conditions (Table 1). Controllable characteristics of the shock-absorber have more wide changing range of resistance force at low piston velocity, when magnetic flux density varies in a range from 0 to 500 mT. Therefore, any controlled shock-absorber is necessary for developing with the annular gap, where as far as possible an average speed of MR fluid flow will be minimum.
The coefficient of relative increase of force (20°C)(80°C) is equal 2 and 7.1 times for different loading conditions (Table 2). Therefore, it is very important to take into account this temperature factor whereas dependences of the performance characteristics of the MR shock-absorber on temperature strongly influence on an active vibroisolation of vehicles.
Table 2Estimation of the performance characteristics of the controlled MR shock-absorber at temperature T= 20 and 80°C
, mm | , Hz | Fmra, N | ||
20°C | 80°C | |||
at 0 mT | ||||
1 | 0.5 | 141 | 71 | 2.0 |
3 | 204 | 80 | 2.6 | |
40 | 0.5 | 325 | 96 | 3.4 |
3 | 531 | 128 | 4.2 | |
at 500 mT | ||||
1 | 0.5 | 5669 | 821 | 6.9 |
3 | 6999 | 1001 | 7.0 | |
40 | 0.5 | 8907 | 1259 | 7.1 |
3 | 11346 | 1592 | 7.1 | |
4. Conclusions
Thereby, the mathematical model of MR fluid flow in an annular channel of the MR shock-absorber taking into account forces of dry friction and gas friction in a pneumatic camera, dependence rheological properties of the MR fluid on shear rate, temperature and magnetic flux density is developed. Performance characteristics of the MR shock-absorber (dependence of force on rod displacement taking into account shock-absorber geometry, rheological properties of the MR fluid, magnetic flux density, temperature) are calculated. The analysis of performance characteristics is made for different loading conditions. The resistance force with growth of magnetic flux density increases 40 times. But the resistance force with growth of temperature from 20°C to 80°C decreases 7 times, in an magnetic field (500 mT), and 2 times, without a field (0 mT). These temperature dependences can be used by development of a control algorithm of shock-absorber performance characteristics for electronic control units.
References
-
Electro-Rheological Fluids and Magneto-Rheological Suspensions. Proceedings of the 12th International Conference, Philadelphia, USA, World Scientific Publishing Company, 2011, p. 748.
-
Korobko E. V., Novikova Z. A., Zhurauski M. A. Rheological and magnetic properties of magnetorheological fluids with complex dispersed phase. Conference book and Book of abstracts of 7th Annual European Rheology Conference, Suzdal, Russia, 2011, p. 114, (in Russian).
-
Wang X., Gordaninejad F. Dynamic modeling of semi-active ER/MR. Fluid Dampers. Proceeding of SPIE Conference on Smart Materials and Structures, Vol. 4331, 2001, p. 82-91.
-
Dixon J. C. The Shock Absorber Handbook. Second Edition, John Wiley & Sons, Ltd., 2007.
-
Derbaremdiker A. D. Vehicle Shock-Absorbers. Moscow, Mashinostroenie, 1985, (in Russian).
-
Paskonov V. M., Polezhaev V. I., Chudov L. A. Numerical Simulation of Heat and Mass Transfer Processes. Moscow: Nauka, 1984, (in Russian).
-
Bilyk V. A., Korobko E. V., Kuzmin V. A. Simulation of performance characteristics of a magnetorheological shock-absorber at the dependence on rheological properties from the magnetic field. Vibroengineering Procedia, Vol. 1, 2013, p. 19-22.
About this article
This research was performed under Belarusian project “Mechanika 1.42” of Government Program of Scientific Research “Mechanics, Technical Diagnostics, Metallurgy” (2014-2015 years).
