Abstract
This study deals with a method to identify multiple cracks in a beam. The novelty of this study is the use of a hierarchical genetic algorithm to detect the number, location, and the extent of multiple cracks. To demonstrate the feasibility of the present method, this algorithm is applied to the identification of double or triple cracks in a beam as well as four cracks. The detected crack locations and sizes are in excellent agreement with the actual ones. The numerical simulation reveal the HGA substantially reduces the total number of FE computation required and they are many orders smaller compared to conventional GA. The results also demonstrate the advantages of HGA from the viewpoints of its ability to avoid premature convergence.
1. Introduction
Many load carrying systems and structures may experience some local damage or accumulate cracks during their functional service. It is well known that cracks are a main cause of structural failure. Sudden failure during high load operation may be catastrophic in terms of human life and property damage. In order to avoid failure caused by cracks, it is desirable to detect cracks before they cause more serious damage and eventual system failure. Therefore, the damage identification problem has recently attracted significant attention [1-3]. There has been numerous of research focusing on model-based methods for damage detection in structures during recent years. Among these efforts, it is believed that the use of vibration data provides the most desirable alternative to actually dismantling structures [1]. In the study of nonlinear mapping relationships between the structural damage indices and various damage statuses, various soft computing techniques, such as the neural networks and genetic algorithm (GA), have been increasingly utilized owing to their excellent pattern recognition capability [1-6].
Among them, GA attracts our attention because it is not necessary to have much data in advance. This is an advantage as compared to the natural frequency-based neural network methods which requires a priori knowledge on both the modal frequencies and the modal shapes to train the neural network and to detect the structural damage. This advantage to genetic algorithms, over the conventional techniques, makes them (GAs) more promising in dealing with complicated, nonlinear, discrete, and multimodal optimization and search problems, such as those considered in this paper.
For example, Liu and Chen [7] employed μGA and finite element method (FEM) to detect the location, area and degree of the flaw in core layer of sandwich plates from time-harmonic response of the plate to harmonic excitation. Ling et al. [8] used the GA to identify a delamination in composite beams by minimizing an objective function based on the changes in natural frequencies of the delaminated beams measured using embedded FBG sensors and calculated using a theoretical constrained beam model. Krawczuk [9] presented the use of the wave propagation approach combined with a genetic algorithm and the gradient technique for damage detection in beam-like structures. Mares and Surace [10] proposed a procedure for locating and quantification of damage in structural systems by means of the concept of residual force vectors and GA.
The majority of state-of-arts studies concerning crack identification in a beam dealt with a single crack case [7-11]. In many cases there is more than one crack on a beam. Then the solutions, or the combinations of parameters characterising the cracks are more and the problem becomes much more complicated. Lee [12] iteratively solved inverse problem for the locations and sizes of the cracks using the Newton-Raphson method as well as the assumption that the number of cracks is known a priori. Friswell et al. [13] used the GA to optimize a discrete weighted objective function to identify the damage located and the eigensensitivity is used to identify the damage extent. Damages at one and two sites have been successfully located in the simulated example of a cantilever beam. During the first phase in Au et al. [14] an elemental energy quotient difference is used to locate the damage. In the second phase a procedure using the so-called micro-GA is implemented to quantify the damage extension by minimizing the error between the measured data (that include frequencies and mode shapes) and numerical results obtained by the finite element method. Lee and Wooh [15] used a coarse searching algorithm to estimate a first-cut location of multiple damages, and then the μGA is applied to find the fine location of the damaged elements within the predetermined zone. He and Hwang [16] used a grey relation analysis to exclude impossible damage locations such that the number of design variables could be reduced and then applied a real-parameter genetic algorithm to identify the actual damage.
Other than the aforementioned two-stage method of identifying the location and extent of multiple structural damages [12-17], Borges et al. [18] proposed several improvements over the standard genetic algorithm to identify the location and extent of multiple damages simultaneously, i.e. two new specialized mutation operators, new forms for fitness function calculation, use of heuristics for initial population generation, and the adoption of discrete values for damage. Nobahari and Seyedpoor [19] established a modified genetic algorithm (MGA) with two new operators (health and simulator operators) to identify the locations and extent of multiple damages. An efficient correlation-based index (ECBI) as the objective function for the optimization algorithm is also introduced.
In spite of the broad scope of applications, the traditional genetic algorithm usually requires a very large number of iterations, and thus high computational cost. To solve the inverse problem of crack detection by means of a GA, it is essential to perform iterative forward computations for each individual. Therefore, the total iteration in resolving the forward problem could be time consuming. Another notable problem is that the objective function of GA usually has many good local optimum solutions which have significantly different damage distributions in comparison with the exact one. This deficiency becomes much more evident for the problem of multiple damages detection. In this study, a hierarchical genetic algorithm (HGA) combined with the forward analysis using the finite element method and the massless rotational spring model for the crack is introduced to identify multiple structural cracks. One illustrative test example is considered to show the performance of the present method. It can be demonstrated that the present hierarchical genetic algorithm (HGA) can avoid premature convergence and trapping into the local optimal solution so that it can provide faster convergence to the near-optimal solution than that of a simple GA.
The organization of the paper is as follows: The next Section illustrates the effect of cracks on natural frequencies. In Section 3, a method of multiple cracks identification using hierarchical genetic algorithm is explained. The simulation and experimental results are presented in Section 4. Section 5 presents conclusions.
2. Finite element simulation of cracked beam
For completeness of presentation the formulation is briefly given here. Figure 1 shows the geometry of a cantilever beam with multiple cracks. The cracks are represented by rotational springs (Figure 2). Parameter and denote the normalized crack location and the normalized crack depth, respectively.
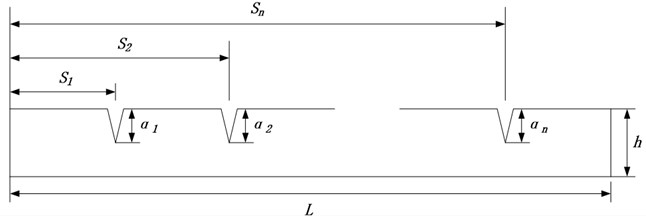
Fig. 1. Cantilever beam with multiple cracks
Fig. 2Representation of multiple cracks by rotational spring

The element stiffness matrix and mass matrix of the th element based on the Euler-Bernoulli theory of length that does not include the crack node are expressed as Eqs. (1), (2):
where , , and are Young’smodulus, the second moment of area, the cross sectional area and the density, respectively.
In the cracked-beam model, a crack on a beam is modeled by placing a torsional spring in the position of the crack. A beam with double cracks and its finite element model are shown in Figure 3, where the crack nodes with three degrees of freedom () are placed at the crack locations and two degrees of freedom () are allocated to the other nodes. The element variable vector of the element that does not include the crack node is while the element variable vectors and are used to describe the motion of the beam on the left and right sides of the crack, respectively. The rotations and are connected through the cracked stiffness matrix as Eq. (3):
where , the torsional stiffness per unit width at the crack, is given by Nandwann and Maiti [20] by Eq. (4):
where is the width of the beam, and:
Fig. 3Cantilever beam with two cracks and its finite element model
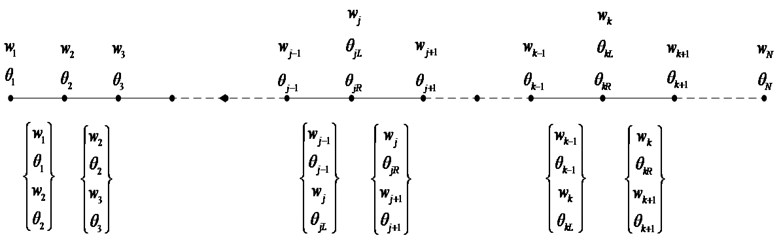
For frequency analysis, the elemental mass and stiffness matrices are derived and then assembled to form the global mass and stiffness matrix. Note that all external forces are zero in the eigenvalue analysis and in the particular case of zero damping, a standard eigenvalue equation can then be written as Eq. (6):
where and are the global mass and stiffness matrices.
3. Identification of multiple cracks using genetic algorithm
In order to address crack identification in terms of an optimization problem with the genetic algorithms, it is necessary to specify an objective function to be minimized. The cost function to be minimized is defined as Eq. (7):
The first term on the right-hand side of Eq. (7), that is symmetric with respect to , is used to suppress intermediate design variables at the end of the optimization. The second term on the right-hand side of Eq. (7), imply that the first 10 resonant frequencies of the optimized structure should be equal to the known resonant frequencies , of the damaged structure within the error tolerance. is the weighting coefficient.
3.1. Introduction to the hierarchical genetic algorithm
To implement the genetic algorithm for the damage identification problem considered here, it is necessary first to define a chromosome for the representation of the design variables, whose values are to be optimized. In this paper, the chromosome has two variables, the normalized crack location and the normalized crack depth associated with the th element in the structural model. The objective function shown in Eq. (7) creates an output from the set of input variables of a chromosome. The goal is to revise the output in some appropriate style by finding the desirable values of input variables.
In this study, an initial study was made on the performance of the conventional genetic algorithm as a solver to Eq. (7), and for the sake of brevity only the final outcomes are provided. The simulation demonstrates that it is considerably probable that the present method may find a healthy element as a damaged one. Therefore, in this study a new hierarchical genetic algorithm (HGA) having a high sensitivity to healthy elements is presented.
Fig. 4Chromosome

The use of the hierarchical genetic algorithm (HGA) is particularly important for the structure or topology as well as the parametric optimization. Unlike the set-up of the conventional GA optimization, where the chromosome and the phenotype structure are assumed to be fixed or pre-defined, HGA operates without these constraints. The hierarchical genetic algorithm was proposed to emulate the formulation of a biological DNA structure. The genes of a complete chromosome are arranged in a hierarchical manner as illustrated in Figure 4, in which there are some parametric genes and control genes. To indicate the activation of the control gene, an integer “1” is assigned for each control gene that is being ignited where “0” is for turning off. When “1” is signaled, the associated parameter genes due to that particular active control gene are activated in the lower level structure. To throw further light on this concept, the following example is used to illustrate the aforementioned functionality of the HGA. A chromosome formed with 6-bit control genes and 6-integer parametric genes is indicated by Figure 4, the corresponding length of chromosome and are three and two, respectively, which indicates that the phenotype in various lengths within the same chromosome formulation. Coding aims to build the relationship between the problem and the individual in genetic algorithms. If the problems are expressed by coding strings, these strings are called an individual or a chromosome. Each individual represents a variable or a part of the problem which is needed to be optimized. In this paper, the locations of cracks and their depth are needed to be optimized by the GA. So these individuals represent the number and location of crack and the corresponding crack depth. For the present method, each control gene is encoded into a binary bit and the activation of the parametric gene is governed by the value of the first-level control genes. While the parametric part represents the depth of crack. Therefore, the standard methods of mutation and crossover may apply independently to each level of genes or even for the whole chromosome if this homogenous. However, the genetic operations that affect the high-level genes can result in changes within the active genes which eventually lead to a change in the lower level genes. By using this encoding technique, the total number of candidate crack elements is significantly reduced. Thus that the genetic operators can be applied only in the ‘active’ elements (damaged) leaving the ‘inactive’ ones (undamaged) unchanged. This is the precise reason why the HGA is not only able to obtain a good set of system parameters, but can also determine a minimized system topology for the crack detection. In this paper, we introduce for each spring element a binary variable which can assume either an ‘active’ or ‘inactive’ state, while each normalized crack depth was denoted as a 10-bit binary number.
3.2. Initial population
A population contains a number of individuals. As regards the specification, there is a higher probability that a larger population will require fewer generations to evolve, i. e. fewer steps in the optimization process before arriving at the optimal solution, although with the increased population size the total processing computer overhead is not necessarily reduced as a consequence. Generally, the population size is chosen from 30 to 100. In order to save the running time, here, the size is chosen 400 for traditional GA while the size is set as 40 for HGA. Because too many uncertain parameters of crack depth would make encoding and evolution too difficult, so we assume that all the crack depth parameters are normalized and chosen on the interval .
3.3. Genetic operators
There are mainly three genetic operations, including, selection, crossover and mutation operations. These genetic operations have key effects on the performances of the genetic algorithm.
3.3.1. Reproduction
In this study, we use the roulette-wheel selection method – a simulated roulette is spun – for this selection process. The response fitness value of every individual is . According to the , a roulette wheel is divided into parts. Here, is the population size. In the selection operation, spinning the roulette wheel, if a consulted point lies in the ith sector, we will choose the th individual. Obviously the area of the sector is larger, and then the probability that the consulted point lies in the sector, is more. This indicates that the better an individual’s fitness is, the more likely it is to be selected. An individual is probabilistically selected from the population on the basis of its fitness and the selected individual is then copied into the next generation of the population without any change.
In this paper, a so-called elitist version of the genetic algorithm was employed whereby the best individual in the current generation is promoted directly to the next generation without undergoing any alteration or mutation. This variation ensures that the fittest member of each successive generation must be either equal or represent an improvement on the currently best candidate. Thus in this application the parameters of crack location and depth will always converge through successive iterations.
3.3.2. Crossover and mutation
In order to facilitate the GA evolution cycle, the Crossover and Mutation operators are required. Selection directs the search toward the best existing individuals but does not create any new individuals. In nature, an offspring has two parents and inherits genes from both. The main operator working on the parents is the crossover operator, the operation of which occurred for a selected pair with a crossover rate . In each new population, there are individuals which are needed crossover operations. In the crossover step, we also keep the same number of chromosomes for each group. After this operation, the individuals with poor performances are replaced by the newly produced offspring.
For selected two chromosomes (parents) from the population, the crossover will be done in two steps: (1) the one-bit binary part representing the control genes and the 10-bit binary number encoding part string representing the parametric genes will do crossover separately; (2) both the control part and the parametric part utilize the uniform crossover.
The mutation operator is always used to keep the diversity of population. Like the crossover, for each selected chromosome from the population, the string of the control neurons and the string of the parametric neurons mutate separately. A simple point mutation is used in control part and the operator exchanges with a given probability each term in parametric part with a randomly selected term in the corresponding complementary subset of the string.
3.4. Design variable reduction (DR) strategy
If we have a priori knowledge about the number of cracks present in a beam, the damage element can be easily identified. When the number of cracks is unknown, however, it will be very difficult to identify even with an advanced method. In the present genetic algorithm-based method, the design variables are assigned to all discretizing nodes, so the number of candidate spring elements is large and there are many local optima in optimization aspect. Therefore, many intermediate design variables may appear at the end of the optimization process [21]. Thus, a so called design variable reduction (DR) strategy is proposed in this paper. DR is based on the idea that the spring elements having normalized crack depth below a prescribed threshold are regarded as the ‘healthy’ ones at the next evolution process. In order to overcome the difficulty of premature of GA, a restart methodology is also adopted. If a few individuals dominate the current generation population, the population will be regenerated at random, while the best individual is still kept in the next generation. It is also worth to note that the DR technique is unnecessary for HGA.
4. Numerical case studies
In order to evaluate the capabilities and effectiveness of the proposed approach for identifying multiple structural damages, a 20-element cantilevered beam is considered. The length, height, and width of the beam are 0.5, 0.02, and 0.01 m, respectively. The mass density is 7860 kg/m3 and the elasticity modulus is 210 GPa. The parameters of the GA are selected here from the experience of our previous work and a trial and error method as follows: the probability of crossover is 0.5, the probability of mutation pm is 0.02, the maximum number of generations is 1000. The convergence of the algorithm is met when the maximum number of generations is attained. In the study, the first ten natural frequencies are used for damage detection and the computational results using an FE model with actual crack positions and sizes are input as measurements.
The conventional genetic algorithm and HGA are applied to the identification of double cracks in a cantilever beam for three simulation cases A, B and C, shown in Table 1 and Table 2. In this test example, the performance of the HGA for crack identification is assessed in comparison with that of the GA.
As can be seen in table 1, both GA and HGA can accurately predict the crack location for case A and B. The average values of depth prediction errors for GA and HGA are 0.75625 % and 0.196875 %, respectively. While the maximum error for depth predictions are 1.52 % for the GA and 0.39 % for the HGA. It is worth noting that the average and the maximum prediction errors for the HGA are less than corresponding values for the GA. It can also be observed that only for case C the crack location and depth are not accurately identified by means of GA and the uncracked elements were regarded as cracked. This is because the multi-crack identification method via genetic algorithm is very sensitive to the changes of natural frequencies. It is worth to noting that the hierarchical genetic algorithm can accurately identify the crack location and depth for all of cases.
By comparing the crack identification results of the aforementioned two methods, some interesting points can be inferred. It can be concluded that the HGA has better performance when compared to the GA. All of the simulation results presented in the tables indicate that the best solutions regarding actual crack detection are obtained by using the method of the hierarchical genetic algorithm. Moreover, the HGA substantially reduces the total number of FE computation required and they are many orders smaller compared to conventional GA. Because of the limitation and instability, it is very difficult to use GA to identify more than double cracks. Therefore, only the predicting results of HGA are given in the subsequent examples. The inverse problem of identifying triple cracks in a cantilever beam is solved for three simulation cases D, E and F. The actual and the detected crack parameters are depicted in Table 3. The error in the detection of crack depth is less than 1 percent and it is zero in the case of detection of crack location.
Table 1The actual and predicted crack location and depth for double cracks (cases A and B)
Case | Desired value (mm) | Prediction (mm) | Error (%) | FEA | Data format | ||||
Location | Depth | Location | Depth | Location | Depth | ||||
A | Crack1 | 100 | 2 | 100 (100) | 2.0206 (1.9952) | 0. (0.) | 1.03 (0.24) | 114800 | GA (HGA) |
Crack2 | 200 | 2 | 200 (200) | 1.9696 (2.0078) | 0. (0.) | 1.52 (0.39) | (36040) | ||
B | Crack1 | 100 | 8 | 100 (100) | 8.0058 (8.0058) | 0. (0.) | 0.0725 (0.0725) | 134800 | GA (HGA) |
Crack2 | 200 | 8 | 200 (200) | 7.9678 (7.9932) | 0. (0.) | 0.4025 (0.085) | (10720) | ||
Table 2The actual and predicted normalized crack location and depth for double cracks (case C)
Case | Crack location (Node numbers) | FEA | |||||
4 | 5 | 6 | 9 | 12 | 13 | ||
Actual | 0 | 0.3 | 0 | 0.4 | 0 | 0 | – |
GA | 0.31579 | 0 | 0.38949 | 0 | 0.04765 | 0.00635 | 97200 |
HGA | 0 | .29990 | 0 | .40029 | 0 | 0 | 9960 |
Table 3The actual and predicted normalized crack location and depth for triple cracks case
Case | Crack location (Node numbers) | ||||||
4 | 7 | 8 | 9 | 11 | 16 | ||
D | Actual | 0.4 | 0.1 | 0 | 0 | 0 | 0.3 |
HGA | 0.40029 | 0.09912 | 0 | 0 | 0 | 0.29990 | |
E | Actual | 0.4 | 0 | 0 | 0 | 0.4 | 0.3 |
HGA | 0.40029 | 0 | 0 | 0 | 0.39966 | 0.29990 | |
F | Actual | 0 | 0 | 0.4 | 0.4 | 0 | 0.3 |
HGA | 0 | 0 | 0.39966 | 0.40029 | 0 | 0.29990 | |
Table 4The actual and predicted normalized crack location and depth considering noise
Case G | Crack location (Node numbers) | |||||
5 | 8 | 9 | 13 | 14 | 15 | |
Actual | 0.3 | 0 | 0.4 | 0 | 0 | 0.6 |
Noise free | 0.29037 | 0 | 0.40029 | 0 | 0 | 0.59980 |
0.15 % | 0.32532 | 0.02033 | 0.37615 | 0 | 0 | 0.60235 |
0.2 % | 0.30435 | 0 | 0.38568 | 0 | 0 | 0.59917 |
0.3 % | 0.30435 | 0 | 0.37996 | 0.00254 | 0 | 0.60108 |
It is assumed in this study that the FE analysis is accurate and any deviations from reality are random noise and not systematic modeling error. For applications to real structures some methods such as finite element model updating can be used to match the modal predictions of the undamaged structure with experimental data. Now the following discussion will be directed to the test using noise contaminated simulated data. The additive noise for the natural frequencies simulating the uncertainty present in experimental measurements and the modeling process is considered here. Table 4 shows the results for four different noise levels: Noise-free, 0.15 %, 0.2 % and 0.3 % noises. It can be observed that the difference between the results with the different low noise levels is negligible. however, the high level noise may induce some adverse effect. The tests performed in the presence of noise imply that the existence of noise in the measured data changes the optimization landscape in a way that a spurious set of new solutions (one with better values of the objective function than that of the correct response) now exists and the algorithm is able to find this solution. The optimization process can be misleading since the optimization algorithm may converge to a ‘better’, but mechanically incorrect, damage distribution.
5. Conclusions
In this paper, a hierarchical genetic algorithm is used to detect multiple cracks in a beam. An integer “1” or “0” is assigned for each control gene which can denote either a damaged or undamaged state. The associated parameter genes representing the normalized depth of crack are activated in the lower level structure. The hierarchical genetic algorithm is more attractive not only because it can avoid premature convergence but also it significantly reduces the total number of finite element analyses in comparison with its predecessor (simple GA). It is concluded in this study that it may be probable to use the described procedure to characterize multiple cracked elements in terms of identifying their numbers, locations, and the level of depth. Numerical results for various damage cases demonstrate that the effectiveness of the present technique. The technique is also attractive from the practical point of view, because we consider only natural frequencies in the objective function.
References
-
Zou Y., Tong L., Steven G. Vibration-based model-dependent damage (delamination) identification and health monitoring for composite structures – A review. Journal of Sound and Vibration, Vol. 230, Issue 2, 2000, p. 357-378.
-
Caddemi S., Morassi A. Detecting multiple open cracks in elastic beams by static tests. Journal of Engineering Mechanics-Asce, Vol. 137, Issue 2, 2011, p. 113-124.
-
Caddemi S., Morassi A. Crack detection in elastic beams by static measurements. International Journal of Solids and Structures, Vol. 44, Issue 16, 2007, p. 5301-5315.
-
Reddy R., Ganguli R. Structural damage detection in a helicopter rotor blade using radial basis function neural networks. Smart Materials & Structures, Vol. 12, Issue 2, 2003, p. 232-241.
-
Zheng S., Li Z., Wang H. Research on delamination monitoring for composite structures based on HHGA-WNN. Applied Soft Computing, Vol. 9, Issue 3, 2009, p. 918-923.
-
Zheng S., Li Z., Wang H. A genetic fuzzy radial basis function neural network for structural health monitoring of composite laminated beams. Expert Systems With Applications, Vol. 38, Issue 9, 2011, p. 11837-11842.
-
Liu G., Chen S. Flaw detection in sandwich plates based on time-harmonic response using genetic algorithm. Computer Methods in Applied Mechanics and Engineering, Vol. 190, Issue 42, 2001, p. 5505-5514.
-
Ling H., Lau K., Cheng L., Jin W. Fibre optic sensors for delamination identification in composite beams using a genetic algorithm. Smart Materials & Structures, Vol. 14, Issue 1, 2005, p. 287-295.
-
Krawczuk M. Application of spectral beam finite element with a crack and iterative search technique for damage detection. Finite Elements in Analysis and Design, Vol. 38, Issue 6, 2002, p. 537-548.
-
Mares S. C. An application of genetic algorithms to identify damage in elastic structures. Journal of Sound and Vibration, Vol. 195, Issue 2, 1996, p. 195-215.
-
Vakil-Baghmisheh M., Peimani M., Sadeghi M., Ettefagh M. Crack detection in beam-like structures using genetic algorithms. Applied Soft Computing, Vol. 8, Issue 2, 2008, p. 1150-1160.
-
Lee J. Identification of multiple cracks in a beam using natural frequencies. Journal of Sound and Vibration, Vol. 320, Issue 3, 2009, p. 482-490.
-
Friswell M., Penny J., Garvey S. A combined genetic and eigensensitivity algorithm for the location of damage in structures. Computers & Structures, Vol. 69, Issue 5, 1998, p. 547-556.
-
Au F., Cheng Y., Tham L., Bai Z. Structural damage detection based on a micro-genetic algorithm using incomplete and noisy modal test data. Journal of Sound and Vibration, Vol. 259, Issue 5, 2003, p. 1081-1094.
-
Lee S., Wooh S. Waveform-based identification of structural damage using the combined finite element method and microgenetic algorithms. Journal of Structural Engineering-Asce, Vol. 131, Issue 9, 2005, p. 1464-1472.
-
He R., Hwang S. Damage detection by a hybrid real-parameter genetic algorithm under the assistance of grey relation analysis. Engineering Applications of Artificial Intelligence, Vol. 20, Issue 7, 2007, p. 980-992.
-
Guo H., Li Z. A two-stage method to identify structural damage sites and extents by using evidence theory and micro-search genetic algorithm. Mechanical Systems and Signal Processing, Vol. 23, Issue 3, 2009, p. 769-782.
-
Borges C., Barbosa H., Lemonge A. A structural damage identification method based on genetic algorithm and vibrational data. International Journal For Numerical Methods in Engineering, Vol. 69, Issue 13, 2007, p. 2663-2686.
-
Nobahari M., Seyedpoor S. Structural damage detection usin an efficient correlation-based index and a modified genetic algorithm. Mathematical and Computer Modelling, Vol. 53, Issue 9-10, 2011, p. 1798-1809.
-
Nandwana B. P., Maiti S. K. Detection of the location and size of a crack in stepped cantilever beams based on measurements of natural frequencies. Journal of Sound and Vibration, Vol. 203, Issue 3, 1997, p. 435-446.
-
Lee J., Kim J., Kim Y. Damage detection by the topology design formulation using modal parameters. International Journal For Numerical Methods in Engineering, Vol. 69, Issue 7, 2007, p. 1480-1498.
About this article
This research was supported by a grant from the Chinese Natural Science Foundation (No. 51075202, 50830201), the Priority Academic Program Development of Jiangsu Higher Education Institutions and Qing Lan Project.
