Abstract
When a vehicle passes through the bridge-subgrade transition zone, the dynamic effects between the vehicle and infrastructure, including track, subgrade will increase greatly. In this paper, a three dimensional model of bridge-subgrade transition zone under moving vehicle in Shuohuang Railway is established. The vehicle is idealized as 18 degree of freedoms multi-body system and the bridge-subgrade transition zone is built using ABAQUS software. With this model, some dynamic responses of bridge-subgrade transition zone under moving vehicle with and without track irregularity are computed. It is concluded that the track irregularity can amplify the dynamic responses in the transition zone significantly.
1. Introduction
To maintain the rapid economic development, China is seeking to solve its current shortage of transport capacity by developing its heavy haul railways. Shuohuang heavy haul railway is the second coal-dedicated railway for China’s West-to-East coal transport. The total length of this line is 588 km, which origins from Shenchi railway station, Shuozhou city, Shanxi province, ends in Huanghua port in Cangzhou city, Hebei Province. In 2011, Shuohuang railway coal shipment hits record high, with 177 million tons of coal, increasing 7.2 million tons or 4.23 % from the year’s transport target [1].
Recently, a new type railway train hauled twenty thousand tons coal has operated since December 27th, 2011 [2]. The total length of this train is 2720 m with total weight 21600 tons. However, the increasing heavy axle loads and high-density transport condition will intensify the damage of the infrastructure, especially in the bridge-subgrade transition zones where the stiffness and deformation change suddenly. Therefore, much more attentions have been paid on the railway transition zones. Dimitrovova et al. presented several simple models to investigate the dynamic responses of the transition zones. In these models, the train loading was regarded as moving load, and the transition zone was modeled as finite/infinite beam with different stiffness supporting by piece-wise homogeneous foundation [3, 4]. Zakeri et al. modeled the ballasted and slab tracks as two dimensional model with two-layer masses and the transition zone as three segments with different specification and stiffness to study the dynamic responses of railway track transition under moving vehicle [5]. Varandas et al. developed a numerical model for the dynamic loads on the ballast caused by trains passing over the culvert and the long-term behavior of the transition zones due to train loading were brought out [6, 7]. In the above mentioned work, several important conclusions have been brought out; however, all of these numerical models are two dimensional and some conditions in reality, including bridge dimensions, subgrade materials should be considered for practical use.
In this paper, a three dimensional bridge-subgrade transition zone model under moving vehicle is developed with finite element method. The vehicle is idealized as 18 degree of freedoms model with one car body, four frames and four wheel sets. The bridge-subgrade transition zone is built using ABAQUS software. Firstly, the dynamic model is validated with the other researcher’s results. Secondly, the dynamic responses of bridge-subgrade transition zone under moving vehicle with and without track irregularity are computed. Thirdly, the dynamic stress and deformation of embankment foundation in the bridge-subgrade transition zone are computed at different vehicle running speeds. From the numerical simulation, it is indicated that the track irregularity may increase these dynamic responses, especially in the transition zone. Another observation is that the embankment foundation above the depth of 1.5 m may undergo much more damage under moving wheel loads.
2. Modeling
In this study, a typical bridge-subgrade transition zone in Shuohuang heavy haul railway was selected, as shown in Fig. 1. The up line from Shenchi to Huanghua is a continuously welded (CWR) 75 kg/m rail at a gauge of 1435 mm, with concrete sleepers at a spacing of 0.6 m to carry the fully laden coal vehicles. However, for the down line the rail mass is 60 kg/m and the sleeper arrangement is the same as the up line (see Fig. 1(a) and (c)). The track substructure consists of ballast and sub-ballast layers. The ballast layer is approximately 0.6 m deep. The bridge is a T-girder concrete bridge with 24 m length (see Fig. 1(b)). The embankment foundation is composed of three distinct layers: gravel of approximately 0.7 m deep, 2.3 m of engineering fill of class A, and sand silt of 3.0 m (see Fig. 1(c)).
Fig. 1Bridge-subgrade transition zone in Shuohuang heavy haul railway

a)

b)

c)
When the vehicle runs over the bridge-subgrade transition zone, the vehicle and the infrastructure, including track, bridge, and subgrade form a complex dynamic interacted system. As shown in Fig. 1, the bridge-subgrade transition zone under moving vehicle can be divided into vehicle model, bridge-subgrade model and contact model.
2.1. Vehicle model
To study the dynamic responses of structures under moving trains, the vehicle is usually regarded as moving loads [8], moving sprung and unsprung mass [9, 10], moving suspend beam [11], and moving multi-body system [12, 13]. In this paper, the vehicle is composed of one car body, four frames and four wheel sets, and these components are connected by primary and secondary suspensions, which are modeled as a system of linear springs and viscous dashpots in the vertical direction. The corresponding parameters of the vehicle system are given in Table 1. With the above assumptions, the car body is designated by vertical and pitching movements. For the frame, vertical and pitching movements are considered. For the wheel set, vertical and rolling movements are considered. In this paper, the vehicle model is built by multi-body dynamic method and the idealized model for the vehicle can be described as 18 degree of freedoms multi-body system.
Table 1Vehicle system parameters
Mass of car body | 91400 kg |
Inertia of car body | 1.33×105 kg·m2 |
Mass of frame | 1786 kg |
Inertia of frame | 420 kg·m2 |
Mass of wheel set | 1257 kg |
Primary suspension stiffness | 13 MN/m |
Primary suspension damping | 3×105 Ns/m |
Secondary suspension stiffness | 4.4 MN/m |
Secondary suspension damping | 4×103 Ns/m |
2.2. Bridge-subgrade model
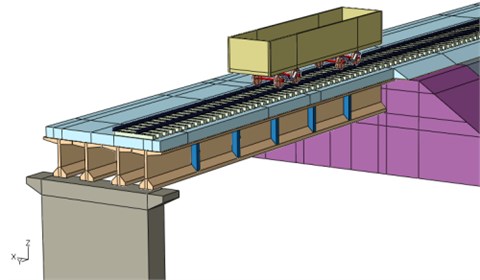
In order to study the dynamic responses of the bridge-subgrade transition zone under moving vehicle, a three dimensional bridge-subgrade model was built using ABAQUS software. The rail and sleepers are modeled using solid elastic elements with eight nodes, and the railway track model is show in Fig. 2. The bridge model, which consisted of multi-span girders and piers, were modeled using 20-node quadratic brick elements. The embankment foundation was modeled as three layers. The length of embankment model in longitudinal was 100 m, the depth of model was 20 m. To overcome the problem of the stress waves, infinite elements were adopted at the boundaries of the embankment. The corresponding parameters of the bridge-subgrade system are given in Table 2.
Fig. 2Track model
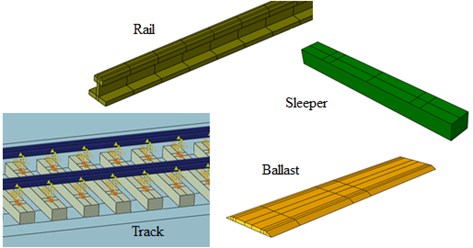
Table 2Bridge-subgrade system parameters
Item | Young’s modulus (N/m2) | Poisson’s ratio | Density (kg/m3) |
Rail (75 kg/m) | 2.1×1011 | 0.3 | 7830 |
Sleeper | 3.5×1010 | 0.22 | 2600 |
Sand gravel | 1.8×108 | 0.3 | 2300 |
Engineering fill of class A | 1.3×108 | 0.3 | 2100 |
Silt sand | 5.0×107 | 0.25 | 1800 |
2.3. Contact model
The contact normal force between the wheel and rail was modeled using nonlinear Hertzian theory. The normal contact force can be given as:
where is the elastic compression between the rail and wheel, is the contact constant [14].
The creep force between the wheel and rail is given as:
where is the coefficient of friction which was set to 0.3.
As discussed above, the finite element model of bridge-subgrade transition zone under moving vehicle is shown in Fig. 3. The bridge-subgrade model under moving vehicle discussed herein is solved by the commercial finite element program ABAQUS, which has an effective explicit solver. The time step is automatically made small so that high-frequency variations are well represented. With an explicit solver, the solution always reaches convergence, which is not always the case with an implicit solver.
Fig. 3Bridge-subgrade zone model under moving vehicle
3. Model validation
To validate the model, some dynamic responses computed from the finite element model are compared with Dong’s model [15]. The parameters of the vehicle load and subgrade can be found in Dong’s thesis.
As shown in Fig. 4, the dynamic stress of soil at the subgrade surface and dynamic deformation of soil at 2.5 m from subgrade surface are compared. It depicts that the dynamic responses computed in this model agree well with Dong’s results [15].
Fig. 4Model comparisons
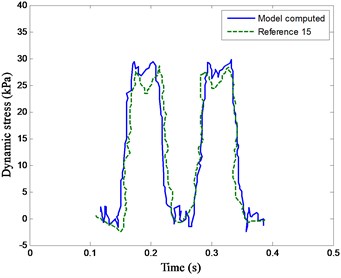
a) Dynamic stress
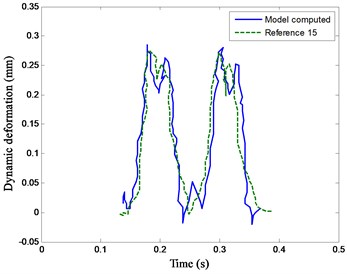
b) Dynamic deformation
4. Numerical simulation
4.1. Effect of track irregularity
Excessive vibration is harmful not only to the running safety of the vehicle, but also to the maintenance of track and subgrade. Therefore, certain tolerance limits are adopted for freight railway. In Chinese specification GB5599-85, the maximum acceleration of vehicle should be less than 0.7 g. For wheel/rail contact force, the upper limit is 250 kN. For ballast and subgrade stress, the maximum values are adopted as follows: 0.5MPa for ballast stress, and 0.15 MPa for subgrade stress.
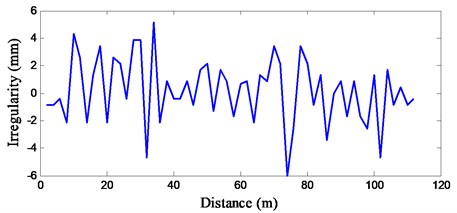
Track irregularity is a major source of vibration for moving trains. For vehicle/bridge (subgrade) interaction system, there are two ways to obtain the track irregularity. One is the one-sided power spectral density (PSD) function, such as PSD functions defined by Federal Railway Administration (FRA), German track [16]. Another is the field testing track irregularity, which can be adopted in the vehicle/bridge (subgrade) interaction system directly [17]. In this section, a measured track irregularity from field testing is adopted in the numerical simulation. The track irregularity used is shown in Fig. 5, which is a stochastic process with amplitude of 6 mm. The wavelength of the track irregularity spectrum has effect on the dynamic responses of the vehicle/bridge (subgrade) system. Generally, the short wave components affect the running safety of the vehicle, while the long wave components affect the car body accelerations and the riding comfort of passengers. In this study, the track irregularities are regarded as a series of discrete points, which can be used to reset in the rail node coordinate system. To investigate the effect of irregularity on the dynamic responses of bridge-subgrade zone under moving vehicle, the acceleration response of vehicle, the wheel/rail contact force, the dynamic stress of ballast and the dynamic stress of subgrade surface are computed. For comparison, when the vehicle runs over the infrastructure at the speed of 100 km/h, both the dynamic responses with irregularity (IRR) and without irregularity (W/O IRR) are shown in Fig. 6.
Fig. 5Track irregularity
As shown in Fig. 6(a), the maximum acceleration of vehicle with irregularity is 0.062 g, with an increase of 71.4 % above the condition without irregularity. However, this value is much less than the allowable limit of 0.7 g. Fig. 6(b) depicts that the maximum value of wheel/rail contact force is about 221 kN, which is much closer to the allowable limit of 250 kN. As shown in Fig. 6(c) and (d), for the dynamic stress of ballast and dynamic stress of soil at subgrade surface, the maximum values are 167.8 kPa and 95.1 kPa, respectively, which are satisfied with the specification. When the track irregularity is considered, the dynamic stresses of ballast and soil at subgrade surface increase 11.4 % and 17.7 %, respectively. It means that the track irregularity can amplify the dynamic responses of bridge-subgrade transition zone, which may increase the infrastructure deterioration. Therefore the track irregularity should be paid much more attention during daily maintenance.
4.2. Dynamic stress and deformation
For embankment foundation, especially in bridge-subgrade transition zone, the components are much more sensitive to failure due to repeated wheel loading. With different moving vehicle speeds at 80, 100 and 120 km/h, the dynamic stress and deformation of embankment foundation in the bridge-subgrade transition zone along with different depth are computed, as shown in Fig. 7.
It can be seen from Fig. 7 that, the dynamic stress and deformation of the embankment foundation increases with an increase of the running speed at the same depth. For the dynamic stress of the embankment foundation, the dynamic stress decrease rapidly from the top to the depth of 1.5 m. However, when the depth is larger than 1.5 m, the dynamic stress decreases very slowly. For the dynamic deformation of the embankment foundation, the dynamic deformation varies along with the depth as linear approximately. It indicates that the embankment foundation above the depth of 1.5 m may undergo much more damage under moving wheel loads.
Fig. 6Dynamic responses
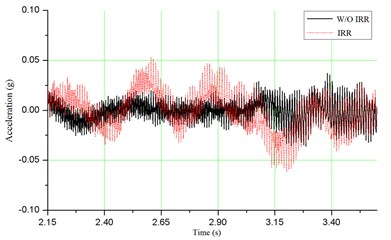
a) Vehicle acceleration
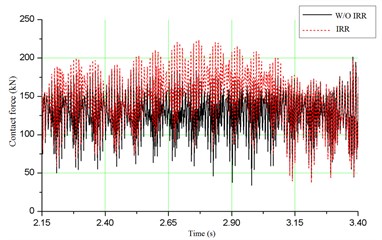
b) Wheel/rail contact force
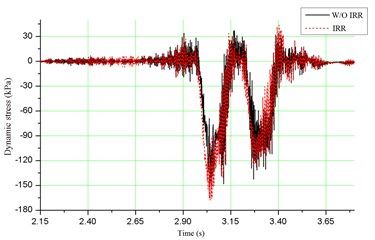
c) Dynamic stress of ballast
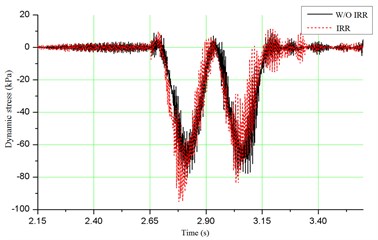
d) Dynamic stress of soil at subgrade surface
Fig. 7Dynamic stress and deformation
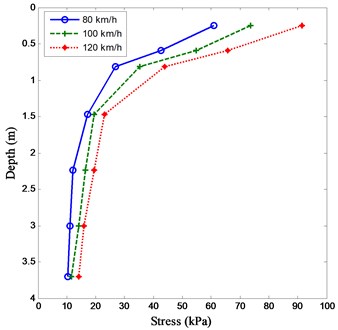
a) Stress
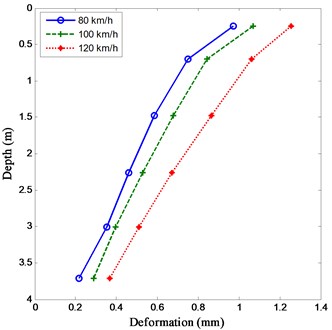
b) Deformation
5. Conclusions
In this paper, a finite element model of bridge-subgrade transition zone under moving vehicle in Shuohuang heavy haul railway is established.
(1) With this model, the dynamic responses, including acceleration response of vehicle, the wheel/rail contact force, the dynamic stress of ballast and the dynamic stress of subgrade surface with irregularity (IRR) and without irregularity (W/O IRR) are computed. It is concluded that the track irregularity can amplify these dynamic responses significantly. Therefore the track irregularity should be paid much more attention during daily maintenance.
(2) The dynamic stress and deformation of embankment foundation in the bridge-subgrade transition zone along with different depth at vehicle running speeds of 80, 100 and 120 km/h are computed. It concluded that the embankment foundation above the depth of 1.5 m may undergo much more damage under moving wheel loads.
References
-
http://en.sxcoal.com/NewsDetail.aspx?cateID=165&id=67988&keyword=Shuohuang.
-
http://www.sasac.gov.cn/n1180/n1226/n2410/n314244/15048612.html, (in Chinese).
-
Dimitrovova Z. A general procedure for the dynamic analysis of finite and infinite beams on piece-wise homogeneous foundation under moving loads. Journal of Sound and Vibration, Vol. 329, Issue 13, 2010, p. 2635-2653.
-
Dimitrovova Z., Varandas J. N. Critical velocity of a load moving on a beam with a sudden change of foundation siffness: applications to high-speed trains. Computers & Structures, Vol. 87, Issue 19-20, 2009, p. 1224-1232.
-
Zakeri J. A., Ghorbani V. Investigation on dynamic behavior of railway track in transition zone. Journal of Mechanical Science and Technology, Vol. 25, Issue 2, 2011, p. 287-292.
-
Varandas J. N., Hölscher P., Silva M. A. G. Settlement of ballasted track under traffic loading: application to transition zones. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, (Online first).
-
Varandas J. N., Hölscher P., Silva M.A. G. Dynamic behaviour of railway tracks on transitions zones. Computers & Structures, Vol. 89, Issue 13-14, 2011, p. 1468-1479.
-
Dimitrovova Z., Rodrigues A. Critical velocity of a uniformly moving load. Advances in Engineering Software, Vol. 50, 2012, p. 44-56.
-
Wang Y. J., Wei Q. C., Shi J., Long X. Y. Resonance characteristics of two-span continuous beam under moving high speed trains. Latin American Journal of Solids and Structures, Vol. 7, Issue 2, 2010, p. 185-199.
-
Wang Y. J., Yau J. D., Wei Q. C. Interaction response of train loads moving over a two-span continuous beam. International Journal of Structural Stability and Dynamics, Vol. 13, Issue 1, 2013, p. 1350002.
-
Wang Y. J., Shi J., Xia Y. Dynamic responses of an elastic beam moving over a simple beam using modal superposition method. Journal of Vibroengineering, Vol. 14, Issue 4, 2012, p. 1824-1832.
-
Shi J., Wang Y. J. Dynamic response analysis of single-span guideway caused by high speed Maglev train. Latin American Journal of Solids and Structures, Vol. 8, Issue 3, 2011, p. 213-228.
-
Xia Y., Ma H. Y., Su D. Strain mode based damage assessment for plate like structures. Journal of Vibroengineering, Vol. 15, Issue 1, 2013, p. 37-45.
-
Zhai W. M. Vehicle-Track Coupling Dynamics. Science Press, Beijing, 2007, (in Chinese).
-
Dong L. Study on Dynamic Characteristics and Deformation Properties of High-Speed Railway Subgrades under Cyclic Loading. Beijing Jiaotong University, Beijing, 2005, (in Chinese).
-
Shi J., Wei Q. C., Zhao Y. Analysis of dynamic response of the high-speed Ems Maglev vehicle/guideway coupling system with random irregularity. Vehicle System Dynamics, Vol. 45, Issue 12, 2007, p. 1077-1095.
-
Xia H., Guo W. W., Xia C. Y., Pi Y. L., Bradford M. A. Dynamic interaction analysis of a Lim train and elevated bridge system. Journal of Mechanical Science and Technology, Vol. 23, Issue 12, 2009, p. 3257-3270.
