Abstract
A new model is proposed based on wavelet theory and genetic algorithms (GAs) in order to improve precision of artificial seismic wave. This model was mainly divided into three parts. Firstly, Mallat method was used to decompose power spectral density function with wavelet base. Then the initial artificial seismic wave was synthesized based on wavelet theory. Thirdly, the iteration processes of artificial seismic wave synthesis were optimized by genetic algorithms. Two numerical examples were given. The first numerical example mainly focuses on the analysis for the initial artificial seismic wave synthesis based on wavelet theory. And the second example mainly focuses on the analysis for the iterative process of artificial seismic wave synthesis based on genetic algorithms. Compared with the conventional method of cosine superposition, this model has smaller error between the calculated acceleration response spectrum and the target response spectrum and can be applied in engineering.
1. Introduction
The theory and methods for artificial seismic wave synthesis have been developed significantly during the last thirty years and have been documented in an increasing number of publications. In order to simulate artificial seismic wave, a rigorous series of tests has to be carried out.
Using the transition relationship between the response spectrum and the power spectrum, Chen et al. (1983) [1] synthesized artificial earthquake ground motions fitted with the standard response spectrum. Considering phase spectrum through the phase correction technique, Hu and He (1986) [2] suggested a simulated ground motion method from the response spectrum. Shinozuka and Deodatis [2] (1991) developed an analytical model for propagating seismic waves that could account for their stochastic characteristics in the time and space domain. From this model, the corresponding sample seismic waves could be digitally generated with great computational efficiency. Conte et al. [3] (1992) used discrete time-varying auto regressive moving average (ARMA) models to describe realistic earthquake ground motion time histories. Deodatis [4] (1996) presented a spectral-representation-based simulation algorithm to generate sample functions of a non-stationary stochastic process with evolutionary power, according to its prescribed non-stationary cross-spectral density matrix. Numerous studies, including those made by Anderson [5] (1987), Hall [6] (1995), and Macrae [7] (2001), indicated that structures experience increased inelastic demands when subjected to near-field ground motions. Zhang and Lou [8] (2001) established a generalized earthquake-wave-motion model, which considered 3D random heterogeneous media, together with existing models for source and realistic geological profiles for sedimentary basins and irregular topography. Both amplitude and frequency non-stationary were incorporated in the model. Zerva and Zervas [9] (2002) suggested that an appropriate simulation technique could be successful in matching the characteristics of the simulated motions with those of the target field. Based on the phase difference spectrum, generating a non-stationary ground motion in both the time and frequency domains was proposed by Yang and Jiang (2002) [10]. Dong et al. [11] (2007) presented an improved local convergent method to simulate multi-point earthquake ground motions. Manoj and Singh [12] (2009) presented a modal to evaluate and predict the blast-induced ground vibration and frequency by incorporating rock properties, blast design and explosive parameters using the artificial neural network (ANN) technique.
Wavelet analysis was applied to engineering problems by several authors. Newland [13, 14] (1994) used wavelets to analyze structural vibrations due to underground and surface traffic. Gurley and Kareem [15] (1999) examined a variety of applications for wavelet analysis including two general methods for simulating non-stationary processes. If a target power spectrum was given, a different modulating function could be used for each wavelet frequency band following a procedure similar to Priestley’s evolutionary spectrum [16] (1965). The procedure proposed by Iyama [17] (1999) was similar to the latter method. A bilinear target spectrum was used for simplicity and the modulating functions, which were expressed as energy release rates. Legrue and Menun [18] (2004) described a procedure that utilized the wavelet decomposition of a recorded acceleration to simulate an ensemble of ground motions that had localized temporal features and variations in the frequency content that were similar to those present in the original record.
In this paper, wavelet theory and genetic algorithms (GAs) are used for establishing the new model for artificial seismic wave synthesis in order to decrease the error between the target response spectrum and the calculated response spectrum of artificial seismic wave.
2. The establishment for artificial seismic wave synthetic model
2.1. The initial artificial seismic wave synthesis based on wavelet theory
According to wavelets multi-resolution analysis theory, is the orthogonal multi-resolution analysis of scaling function , the scaling relation (1) is given as:
in which:
and
It is assumed that (; ) is the orthogonal multi-resolution analysis, then can be found to make the Eq. (4) exist:
The scaling function is used to construct function:
The dilation and translation of constructs orthogonal basis of , in which:
and
when:
where is defined as wavelet function.
Mallat method is used to decompose power spectral density function with wavelet. The basic idea is , which is defined as the approximation under resolving capability of finite energy signals, can be further decomposed into and , which is defined as the detail between resolving capability and . The decomposition course is shown as Fig. 1.
Fig. 1The decomposition process of signals at different frequency band
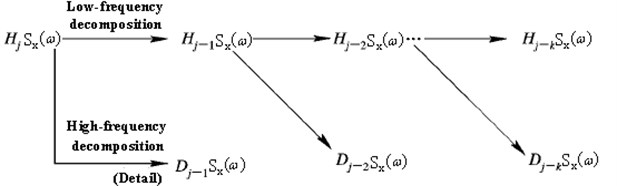
The coefficient of two-scale equations , can be obtained as:
And Eq. (10), (11) and (12) can be obtained as:
Then the stationary process by wavelet basis is given as:
where is the random phase angle obeyed homogeneous distribution.
And the power spectral density function is given as:
where is the target response spectrum, is the probability of the calculated acceleration response spectrum greater than the target response spectrum, is damping ratio, is time step. The is shown as Fig. 2. In Fig. 2, is the characteristic period of ground and is amplification factor.
Fig. 2The target response spectrum SaT(ωk)
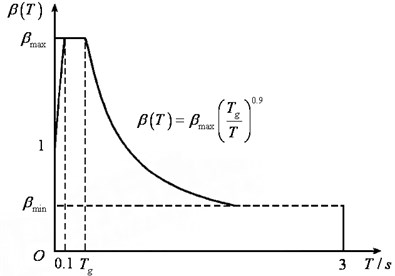
In order to reflect the non-stationary seismic wave , multiplied by the envelope function is adopt as:
where is given as:
where the range of attenuation coefficient is 0.1-1.0. and are the first and last time of the stationary process, respectively. is the duration of seismic wave, usually . In order to improve the frequency resolution, it usually makes and when .
2.2. The iterative process of artificial seismic wave synthesis based on genetic algorithms
Genetic algorithms (GAs) are adaptive heuristic search algorithm premised on the evolutionary ideas of natural selection and genetic. Algorithm is started with a set of solutions (represented by chromosomes) called population. Solutions from one population are taken and used to form a new population. This is motivated by a hope, that the new population will be better than the old one. Solutions which are selected to form new solutions (offspring) are selected according to their fitness-the more suitable they are the more chances they have to reproduce. This is repeated until some condition (for example number of populations or improvement of the best solution) is satisfied. Genetic algorithms are usually used for solving the optimization problem, whose objective function is implicit expression. The details on seismic wave synthesis based on genetic algorithms are discussed as follow.
Because approximate transformational relation between the target response spectrum and the power spectrum is adopted in the initial step of artificial seismic wave synthesis, the numerical iterative process of calculated acceleration response spectrum must be supplemented in order to fit the target response spectrum .
The error between and at frequency is defined as:
The total error is defined as:
where is the number of .
The iteration step of is calculated as:
where are modifying weights at frequency .
When and are respectively used as the optimization variables and minimal optimization goals, are given through solving the following optimization problem as:
If the maximum value of need to control, the optimization problem (20) can be revised as:
where is penalty function.
The objective functions of optimization problem (20) or (21) are implicit expressions, so GAs can be used to solve them.
Through solving optimization problem (20) or (21) by GAs, can be obtained. Through substituting into Eq. (19) and then substituting Eq. (19) into Eq. (13) and (15), the iterative process of artificial seismic wave synthesis can be calculated.
3. Numerical analysis
3.1. Numerical example 1
This section mainly focuses on the analysis for the initial artificial seismic wave synthesis based on wavelet theory. The parameters of the initial artificial seismic wave are given as follow: The first and last time of the stationary process are given as 2 s, 16 s. The duration of seismic wave is given as 20 s. The attenuation coefficient is given as 0.80. The maximum value of amplification factor is given as 2.0. The characteristic period of ground is given as 0.40. The time step is given as 0.01 s. The probability of the calculated acceleration response spectrum greater than the target response spectrum is given as 0.15. The damping ratio is given as 0.05. The peak acceleration is 0.251 where is the acceleration of gravity. The initial artificial seismic wave is synthesized as Daubechies wavelet base (db1) and Daubechies wavelet base (db4), and the power spectral density function is decomposed to 4 levels.
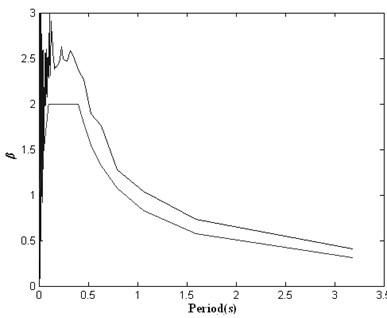
The initial artificial seismic wave generated by conventional method of cosine superposition and the calculated response spectrum of which are shown as Fig. 3 and 4, respectively. The initial artificial seismic wave generated by wavelet base (db1) method and the calculated response spectrum of which are shown as Fig. 5 and 6, respectively. The initial artificial seismic wave generated by wavelet base (db4) method and the calculated response spectrum of which are shown as Fig. 7 and 8, respectively.
Fig. 3The initial artificial seismic wave generated by conventional method of cosine superposition
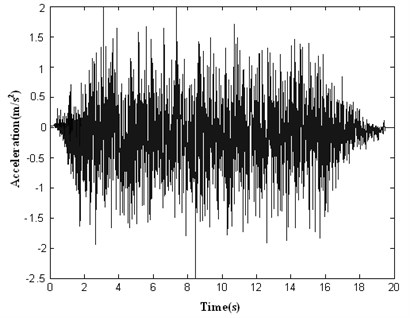
Fig. 4Response spectrum of initial artificial seismic wave generated by conventional method of cosine superposition compared with the target response spectrum
3.2. Numerical example 2
This section mainly focuses on the analysis for the iterative process of artificial seismic wave synthesis based on genetic algorithms. The parameters of the initial artificial seismic wave are given as follow: The first and last time of the stationary process are given as 2 s, 8 s. The duration of seismic wave is given as 16 s. The attenuation coefficient is given as 0.80. The maximum value of amplification factor is given as 2.0. The characteristic period of ground is given as 0.40. The time step is given as 0.01 s. The probability of the calculated acceleration response spectrum greater than the target response spectrum is given as 0.15. The damping ratio is given as 0.05. The peak acceleration is 0.251 where is the acceleration of gravity.
Fig. 5The initial artificial seismic wave generated by wavelet base (db1) method
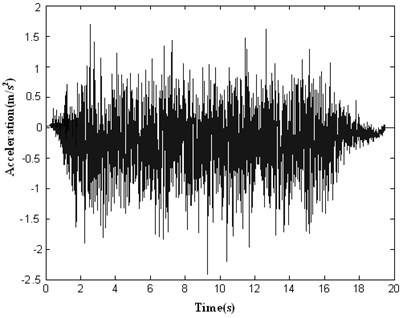
Fig. 6Response spectrum of initial artificial seismic wave generated by wavelet base (db1) method compared with the target response spectrum
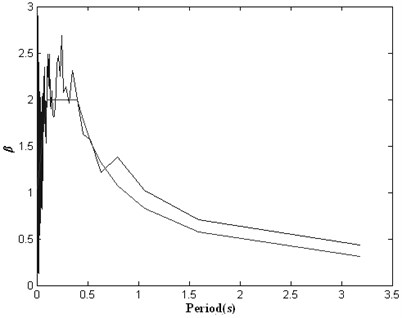
Fig. 7The initial artificial seismic wave generated by wavelet base (db4) method
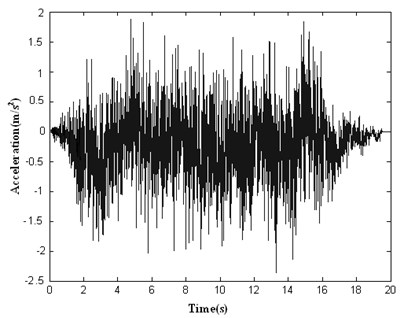
Fig. 8Response spectrum of initial artificial seismic wave generated by wavelet base (db4) method compared with the target response spectrum
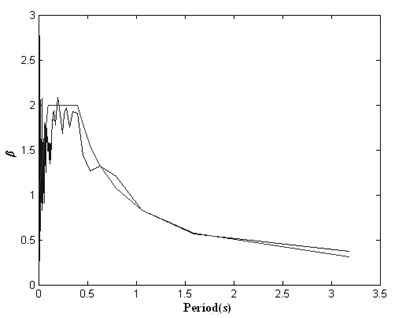
Fig. 9The artificial seismic waves generated by the conventional method of cosine superposition
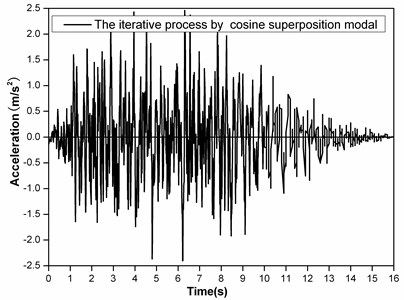
Fig. 10The artificial seismic waves generated by this paper’s method
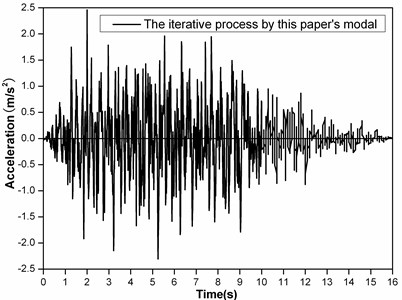
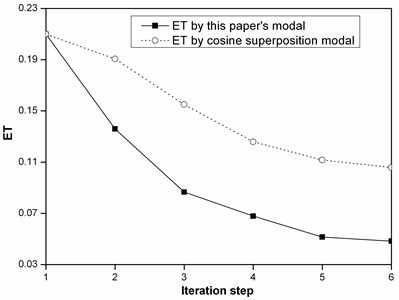
The artificial seismic waves generated by the conventional method of cosine superposition and this paper’s method based on GAs are shown as Fig. 9 and 10, respectively. The calculated response spectrums of artificial seismic waves generated by the conventional method of cosine superposition and this paper’s method compared with the target response spectrum are shown as Fig. 11. The total error with iteration steps are shown as Fig. 12.
Fig. 11The response spectrums of artificial seismic waves generated by the conventional method
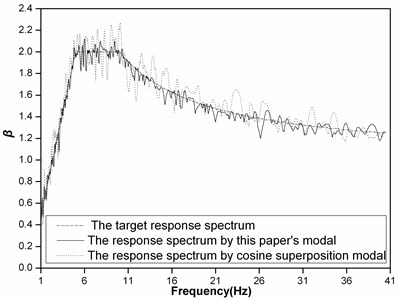
Fig. 12The total error with iteration steps
4. Discussion
From the analysis of Fig. 3-8, it shows that Daubechies wavelet base (db4) is better than Daubechies wavelet base (db1) to generate initial artificial seismic wave comparing with the effect of using these wavelet bases. And the total error by using Daubechies wavelet base is smaller than by using the conventional method of cosine superposition. From the analysis of Fig. 9-12, it shows that the total error by using by using this paper’s model based on GAs is 3 times smaller than the conventional method of cosine superposition. And the descent speed of the total error by using this paper’s model based on GAs is higher than by using the conventional method of cosine superposition. From what has been discussed above, it shows that this paper’s model can improve precision of artificial seismic wave and can be applied in engineering.
5. Conclusion
Artificial seismic wave synthesis model is established based on wavelet theory and genetic algorithm. The initial artificial seismic wave synthesis is optimized by wavelet theory. The iteration processes of artificial seismic wave synthesis are optimized by genetic algorithms. The result showed that the total error between calculated and target response spectrum by this paper’s method is smaller than by conventional method of cosine superposition.
References
-
Chen Y. Q., Liu X. H., Gong S. L. The artificial earthquake ground motions compatible with standard response spectra. Journal of Building Structures, Vol. 4, Issue 1, 1983, p. 34-43, (in Chinese).
-
Shinozuka M., Deodatis G. Stochastic wave models for stationary and homogeneous seismic ground motion. Structural Safety, Vol. 10, Issue 1-3, 1991, p. 235-246.
-
Conte J. P., Pister K. S., Mahin S. A. Nonstationary ARMA modeling of seismic motions. Soil Dynamics and Earthquake Engineering, Vol. 11, Issue 7, 1992, p. 411-426.
-
Deodatis G. Non-stationary stochastic vector processes: seismic ground motion applications. Probabilistic Engineering Mechanics, Vol. 11, Issue 3, 1996, p. 14-167.
-
Anderson J. C., Bertero V. V. Uncertainties in establishing design earthquakes. Journal of Structural Engineering, Vol. 113, Issue 1, 1987, p. 1709-1724.
-
Hall J. F., Heaton T. H., Halling M. W., Wald D. J. Near-source ground motion and its effects on flexible buildings. Earthquake Spectra, Vol. 11, Issue 1, 1995, p. 569-605.
-
Macrae G. A., Morrow D. V., Roeder C. W. Near-fault ground motion effects on simple structures. Journal of Structural Engineering, Vol. 127, Issue 1, 2001, p. 996-1004.
-
Zhang R. R., Lou M. Seismic wave motion modeling with layered 3D random heterogeneous media. Probabilistic Engineering Mechanics, Vol. 16, Issue 1, 2001, p. 381-397.
-
Zerva A., Zervas V. Spatial variation of seismic ground motions: an overview. Applied Mechanics Reviews, Vol. 55, Issue 3, 2002, p. 271-297.
-
Yang Q. S., Jiang H. P. Generation of response spectrum-compatible ground motions based on phase-difference spectrum. Earthquake Engineering and Engineering Vibration, Vol. 22, Issue 1, 2002, p. 32-38, (in Chinese).
-
Dong R. B., Zhou J., Feng X. A local convergent method for simulating multi-point earthquake ground motion. Journal of Sound and Vibration, Vol. 26, Issue 4, 2007, p. 5-9, (in Chinese).
-
Khandelwal M., Singh T. N. Prediction of blast-induced ground vibration using artificial neural network. International Journal of Rock Mechanics and Mining Sciences, Vol. 46, Issue 7, 2009, p. 1214-1222.
-
Newland D. E. Wavelet analysis of vibration. Part 1: Theory. Journal of Vibration and Acoustics, Vol. 116, Issue 1, 1994, p. 409-416.
-
Newland D. E. Wavelet analysis of vibration. Part 2: Wavelet maps. Journal of Vibration and Acoustics, Vol. 116, Issue 1, 1994, p. 417-425.
-
Gurley K., Kareem A. Applications of wavelet transforms in earthquake wind and ocean engineering. Engineering Structures, Vol. 21, Issue 1, 1999, p. 149-167.
-
Priestley M. B. Evolutionary spectra and non-stationary processes. Journal of the Royal Statistical Society Series B, Vol. 27, Issue 1, 1965, p. 204-237.
-
Iyama J., Kuwamura H. Application of wavelets to analysis and simulation of earthquake motion. Earthquake Engineering and Structural Dynamics, Vol. 28, Issue 1, 1999, p. 255-272.
-
Legrue J., Menun C. Simulation of non-stationary ground motions using wavelets. 13th World Conference on Earthquake Engineering Vancouver, Vol. 1, Issue 1-6, 2004, p. 296.
About this article
This study was supported by Project supported by the National Natural Science Foundation of China (Grant No. 51109029, 51178081, 51138001, 51009020) and China Postdoctoral Science Foundation (Grant No. 20110491535).
