Abstract
Every structure which is having some mass and elasticity is said to vibrate. Natural frequency is the one of the most important parameter associated with engineering vibration. In nature every structure has its own natural frequency. Whenever the natural frequency of the structure coincides with the frequency of external applied load, excessive deflections will occur and the structure will be failed. To avoid such condition one must be aware of the operating frequencies of the materials or structures under various conditions like simply supported, clamped and cantilever boundary conditions. There are many methods to evaluate the natural frequency of the structures. in this method the authors developed a method called “coupled displacement field method” which reduces computational efforts compared with the other methods and which is successfully applied for the Hinged-Hinged boundary condition of a tapered (rectangular cross section) Timoshenko beam and calculated the fundamental frequency parameter values and compared the results with existing literature. The results obtained in this method are very close to the existing literature.
1. Introduction
Research on vibrations of beams has been doing by so many authors for a long period of time. So far, many authors have found different methods to find the free vibration behaviour of shear flexible beams, some of them are as follows.
Abrate S. [1] analyzed the free vibration of nonuniform beams with general shape and arbitrary boundary conditions. Simple formulas are presented for predicting the fundamental natural frequency of non-uniform beams with various end support conditions.
Byoung Koo Lee et al. [2] studied on “Free vibrations of tapered Beams with general boundary condition”. This method involving the finding of the ordinary differential governing equation of beams which can be solved by numerical methods. the natural frequencies are calculated by combining the Runge Kutta method and the determinant search method.
De Rosa M. A. et al. [3] studied the dynamic behaviour of beams with linearly varying cross-section. in this method. The equation of motion is solved in terms of Bessel functions, and the boundary conditions lead to the frequency equation which is a function of four flexibility coefficients.
De Rosa M. A. et al. [4] studied the Natural vibration frequencies of Tapered beams by using Euler-Bernoulli beam theory in the presence of an arbitrary number of rotationally, axially and elastically flexible constraints. In this method, the dynamic analysis is performed by means of the so-called cell discretization method (CDM), according to which the beam is reduced to a set of rigid bars, linked together by elastic sections, where the bending stiffness and the distributed mass of the bars is concentrated.
Firouz-Abadi R. D. et al. [5] studied the transverse free vibration of a class of variable-cross-section beams is investigated using the Wentzel, Kramers, Brillouin (WKB) approximation in which the governing equation of motion of the Euler-Bernoulli beam including axial force distribution is utilized to obtain a singular differential equation in terms of the natural frequency of vibration and a WKB expansion series is applied to find the solution.
Izabela Zamorska [6] used the Green’s function method for the free vibration problem of non-uniform Bernoulli-Euler beams, to find the Green’s function of the fourth order differential operator, occurring at the beam’s equation of motion, the power series method is proposed.
Mahmoud A. A. et al. [7] applied the differential transformation method (DTM) for free vibration analysis of beams with uniform and non-uniform cross sections. Natural frequencies and corresponding normalized mode shapes are calculated for different cases of cross section and boundary conditions. MATLAB code is designed to solve the differential equation of the beam using the differential transformation method.
Mehmet Cem Ece, et al. [8] studied the vibrations of an isotropic beam which has a variable cross-section. In this, the Governing equation is reduced to an ordinary differential equation in spatial coordinate for a family of cross-section geometries with exponentially varying width. Analytical solutions of the vibration of the beam are obtained for three different types of boundary conditions associated with simply supported, clamped and free ends. Natural frequencies and mode shapes are determined for each set of boundary conditions.
Mohamed Hussien Taha et al. [9] used a “mathematical model for vibrations of non-uniform flexural beams” they presented a simplified mathematical model for free vibrations of nonuniform viscoelastic flexural beams is presented. The mass intensity, the material damping intensity and the flexural stiffness of the beam are assumed varying as power functions along the beam. An analytical solution for the fourth order differential equation of beam vibration under appropriate boundary conditions is obtained by factorization and calculated Mode shapes and damped natural frequencies of the beam are obtained for wide range of beam characteristics.
Rossi R. E. and Laura P. A. A. [10] determined the natural frequencies and dynamic behavior vibration of linearly tapered beams subjected to different combinations of edge supports by finite element algorithmic procedures.
Stanisław Kukla, Izabela Zamojska [11] applied the Green’s function method in frequency analysis of a beam with varying cross section. The beam carries an arbitrary number of attached discrete systems. The exact solution of the problem concerns a beam with quadratically varying cross-section area.
Zhou D. and Cheung Y. K. [12] studied the vibrational characteristics of tapered beams with continuously varying rectangular cross-section of depth and breadth proportional to and respectively, where both and are arbitrary real numbers for a truncated beam and arbitrary positive numbers for a sharp ended beam and is the axial co-ordinate measured from the sharp end of the beam. They used the Bernoulli- Euler theory of bending is used to describe the motion of the beam. They obtained the eigen frequency equation by the Rayleigh-Ritz method and The effect of the location the convergency is discussed.
In the present method the concept of Coupled Displacement Method is presented for the vibration analysis of tapered Timoshenko beams, where the transverse displacement is expressed in terms of total rotation and its derivatives depending on the transverse shear deformation theory, in which the number of un known coefficients is brought down to exactly in the coupled displacement field method. To demonstrate the efficacy of the proposed method, the expressions for fundamental frequency are obtained for tapered shear flexible Timoshenko beams with hinged-hinged type of boundary condition. The numerical results presented in this paper are matching very closely with the existing literature.
2. Coupled displacement field method (CDF)
2.1. Coupling equation
The concept of coupled displacement field is explained in detail. in the Couple Displacement Field Method (CDF) with the single term admissible function for , the function for is derived using the coupling equation. The coupling equation has been derived from the Timoshenko beam theory and an admissible function for which satisfies all the applicable boundary conditions and the symmetric condition is assumed in the beam domain. The coupled lateral displacement distribution is evaluated from the coupling equation.
Fig. 1Tapered Timoshenko beam with linearly varying height (depth)
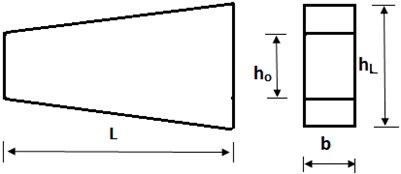
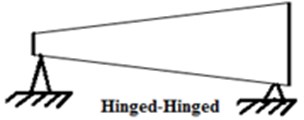
Fig. 2Tapered (rectangular cross section) Timoshenko Hinged-Hinged beam
2.2. Linear free vibrations
From The kinematics of a shear flexible beam theory (based on the Timoshenko beam theory):
where is the axial displacement and is the transverse displacements at an any point of the beam, is the distance of the any point from the neutral axis, is the transverse displacement and is the total rotation anywhere on the beam axis and , are the independent spatial variables. The axial and shear strains are given by:
Now, the expressions for the strain energy ‘’ and the work done by the externally applied loads are given by:
where is the flexural rigidity, is the shear rigidity, is the shear correction factor (taken as 5/6 in the present study), is the static lateral load per unit length acting on the beam, is the Young’s modulus, is the shear modulus, is the area moment of inertia, is the area of cross section, is the axial coordinate and is the length of the beam. Applying the principle of minimization of total potential energy, as:
The following equilibrium equations can be obtained:
where is total rotation, is transverse displacement.
Eqs. (8) and (9) are coupled equations and can be solved for obtaining the solution for the static analysis of the shear deformable beams.
A close observation of Eq. (8) shows that it is dependent on the load term ‘’ and Eq. (9) is independent of the load term ‘’. Hence, Eq. (9) is used to couple the total rotation and the transverse displacement , so that the two undetermined coefficients problem (for single term admissible function) becomes a single undetermined coefficient problem and the resulting linear free vibration problem becomes much simpler to solve.
The concept of coupled displacement field method is explained in detail. In Coupled Displacement Field method (CDF) with the single term admissible function for , the function for is derived using the coupling Eq. (9). An admissible function for which satisfies all the applicable boundary conditions and the symmetric condition is assumed in the beam domain.
For hinged-hinged tapered Timoshenko beam, assumed total rotation is:
where is the central lateral displacement of the beam which is also the maximum lateral displacement.
Rewriting Eq. (9):
By integrating the above equation, lateral displacement can be obtained as:
where , .
It may be noted here that because of the coupled displacement field concept the transverse displacement () distribution contains the same undetermined coefficient “” as the distribution and satisfies all the applicable essential boundary and symmetric conditions:
2.3. Linear free vibrations
For an assumed distribution, the coupled displacement field for the lateral displacement is evaluated, after the lateral displacement is calculated, linear free vibrations can be studied.
Using the principle of conservation of total energy at any instant of time constant.
As the depth of the beam is not uniform throughout the length, the expression for and are given as:
where:
and , , are the strain energy, kinetic energy and young’s modulus respectively. is the mass density of the material of the beam, is the radian frequency, and are the height of the beam at left end 0 and the right end respectively, and are cross sectional area and area moment of inertia at left end, is the area at any cross section, is the moment of inertia at any cross section, is the taper ratio.
Substituting Eqs. (10), (14), (18) in Eq. (16) and after simplification:
Substituting Eqs. (10), (14), (18) in Eq. (17) and after simplification:
Applying the principle of minimization of total potential energy:
and after simplification, the non-dimensional fundamental frequency parameter 𝜆 is obtained and as:
where is the non dimensional fundamental frequency parameter, (slenderness ratio) and is radius of gyration
If the taper ratio is zero, then the above equation becomes:
The above equation is applicable for uniform beam as the taper ratio is zero.
Table 1Fundamental Frequency (λ1/2) values for a Hinged-Hinged (Rectangular cross section) tapered Timoshenko beam
Taper ratio () | Slenderness ratio () | |||||||||
10 | 20 | 40 | 80 | 100 | 500 | |||||
CDF Method | Ref [10] | CDF Method | Ref [10] | CDF Method | CDF Method | CDF Method | Ref [10] | CDF Method | Ref [10] | |
0 | 8.3913 | 8.388 | 9.4108 | 9.411 | 9.7471 | 9.8384 | 9.8496 | 9.850 | 9.8688 | 9.869 |
0.1 | 8.6917 | 8.683 | 9.8416 | 9.829 | 10.226 | 10.331 | 10.344 | – | 10.366 | – |
0.15 | 8.8435 | – | 10.059 | – | 10.469 | 10.581 | 10.595 | – | 10.619 | – |
0.20 | 8.9962 | 8.955 | 10.279 | 10.22 | 10.714 | 10.833 | 10.848 | – | 10.873 | – |
0.25 | 9.1496 | – | 10.499 | – | 10.960 | 11.086 | 11.102 | – | 11.129 | – |
0.30 | 9.3036 | 9.205 | 10.721 | 10.61 | 11.208 | 11.342 | 11.358 | – | 11.386 | – |
0.35 | 9.4581 | – | 10.944 | – | 11.457 | 11.598 | 11.616 | – | 11.646 | – |
0.4 | 9.6128 | – | 11.168 | – | 11.707 | 11.856 | 11.875 | – | 11.906 | – |
0.45 | 9.7676 | – | 11.3927 | – | 11.9596 | 12.116 | 12.1356 | – | 12.168 | – |
0.5 | 9.9226 | – | 11.6178 | – | 12.2124 | 12.377 | 12.3973 | – | 12.432 | – |
0.55 | 10.077 | – | 11.8435 | – | 12.4662 | 12.638 | 12.6602 | – | 12.696 | – |
0.6 | 10.232 | – | 12.0697 | – | 12.7209 | 12.901 | 12.9242 | – | 12.962 | – |
0.65 | 10.386 | – | 12.2963 | – | 12.9764 | 13.165 | 13.1892 | – | 13.229 | – |
0.7 | 10.540 | – | 12.523 | – | 13.232 | 13.430 | 13.455 | – | 13.497 | – |
0.75 | 10.694 | – | 12.750 | – | 13.489 | 13.696 | 13.722 | – | 13.765 | – |
0.8 | 10.847 | – | 12.977 | – | 13.747 | 13.963 | 13.989 | – | 14.035 | – |
0.85 | 11.000 | – | 13.204 | – | 14.005 | 14.230 | 14.258 | – | 14.305 | – |
0.9 | 11.151 | – | 13.431 | – | 14.264 | 14.498 | 14.527 | – | 14.577 | – |
0.95 | 11.303 | – | 13.658 | – | 14.523 | 14.767 | 14.797 | – | 14.849 | – |
1 | 11.453 | – | 13.885 | – | 14.783 | 15.036 | 15.068 | – | 15.122 | – |
3. Results
The concept of Coupled displacement field method is used to determine the fundamental frequencies of tapered shear flexible beams, with most practically used boundary condition. The boundary conditions of the beams considered is hinged-hinged, one with axially immovable ends. Suitable single-term trigonometric functions is used to represent the total rotation in the present study, the corresponding coupled lateral displacement is derived using the present concept. The numerical results are obtained in terms of non-dimensional fundamental frequency parameter, for various slenderness ratios () and taper ratios ().
The present results, in terms of slenderness ratios () and taper ratios () for a tapered shear flexible hinged-hinged beam, are presented in Table 1. For the sake of comparison and validation of the proposed method, the results obtained by present coupled displacement method are compared with Rossi R. E. and Laura P. A. A. and are also included in this table. The value obtained for non-dimensional fundamental frequency parameter for the given uniform Timoshenko beam is exactly matching with the existing literature. This is because the admissible function assumed for the total rotation is exact for this classical problem.
4. Conclusions
This method is having less complexity compared to other energy methods as the computational efforts are being reduced to half compared to Rayleigh-Ritz method. This formulation can also be used for the study of the free vibration analysis of shear flexible structural members other than Timoshenko beams.
References
-
Abrate S. Vibration of non-uniform rods and beams. Journal of Sound and Vibration, Vol. 185, Issue 4, 1995, p. 703-716.
-
Byoung Koo Lee, et al. Free vibrations of tapered Beams with general boundary condition. Journal of Civil Engineering, Vol. 6, Issue 3, 2002, p. 283-288.
-
De Rosa M. A., Auciello N. M. Free vibrations of tapered beams with flexible ends. Journal of Computers and Structures, Vol. 60, Issue 2, 1996, p. 197-202.
-
De Rosa M. A., Lippiello M. Natural vibration frequencies of tapered beams. Journal of Engineering Transactions, Vol. 57, Issue 1, 2009, p. 45-66.
-
Firouz-Abadi R. D, et al. An asymptotic solution to transverse free vibrations of variable-section beams. Journal of Sound and Vibration, Vol. 304, 2007, p. 530-540.
-
Izabela Zamorska Free Transverse vibrations of non-uniform beams. Scientific Research of the Institute of Mathematics and Computer Science, Vol. 9, Issue 2, 2010, p. 244-250.
-
Mahmoud A. A., et al. Free vibrations of uniform and non-uniform Euler beam using differential transformation method. Asian Journal of Mathematics and Applications, Vol. 2013, 2013, p. 1-16.
-
Mehmet Cem Ece, et al. Vibration of a variable cross-section beam. Journal of Mechanics Research Communications, Vol. 34, 2007, p. 78-84.
-
Mohamed Hussien Taha, Samir Abohadima Mathematical model for vibrations of non-uniform flexural beams. Journal of Engineering Mechanics, Vol. 15, Issue 1, 2008, p. 3-11.
-
Rossi R. E., Laura P. A. A. Numerical experiments on vibrating, linearly tapered Timoshenko beams. Journal of Sound and Vibration, Vol. 168, Issue 1, 1993, p. 179-183.
-
Stanisław Kukla, Izabela Zamojska Application of the Green’s function method in free vibration analysis of non-uniform beams. Scientific Research of the Institute of Mathematics and Computer Science, Vol. 4, Issue 1, 2005, p. 87-94.
-
Zhou D., Cheung Y. K. The free vibration of a type of tapered beams. Journal of Computer Methods in Applied Mechanics and Engineering, Vol. 188, 2000, p. 203-216.
About this article
The authors express their gratitude to (JNTUK) Jawaharlal Nehru Technological University, Kakinada, AP, India for providing the facilities to carry out their research successfully. And also they thank the authorities of University College of Engineering (A), JNTUK, Kakinada, for extending the necessary support for publishing the paper under TEQIP-II (Technical Education Quality Improvement Programme).
